Капутин Ю.Е., Ежов А.И., Хейнли С. Геостатистика в горно-геологической практике
Подождите немного. Документ загружается.


Полученны
й
в
результ
ате
такой
обрабо
тки
единый
файл
опробованИя
скважин
затем
объ
ед
и
н
я
етс
я
с
имеющими
ся
данными
по
ЛИТОЛОГJ-lИ,
геомеханике,
ги
д
рогеол
огии
и
т
.
п
.,
если
эти
данные
были
введены
отдельно
с
ука
з
ани
е
м
ин
те
р
вал
о
в
,
отличающихся
от
рядового
опробования.
Посл
е
этого
все
вве
д
енные
сведеlll1Я
о
месторождении
должнь
быть
'
проверены
на
к
о р
рект
но
сть
и
о тсут
ствие
ошибок
.
Обычно
это
самый
трудоемкий
пр
оцесс,
т р
ебующий
больших
,затрат
времени.
В
частности
в
сис
т
ем
е
Д
а
т
а
м
ай
н
с
уществует
набор
стандартных
про
верок
корректнос
т и ис
х
одных
д
анных
,
ко
то
ры
е
помогают
и
збавиться
от
самых
грубых
ошибок,
п
е
рен
есе
н
н
ы
х
и
з
первичных
материалов
или
полученных
в
р
ез
ультате
н
е
брежног
о
ввода
данн
ы
х
в
компьют
ер.
Однако
окончательное
выя
вле
н
ие
и
исправл
е
ние
ошибок
прои
з
водитсн
путем
вывода
и
рассм
ат
ри
в а
н
и
я
на
экране
компьютера
совместно
контуров
рудных
тел
,
про
б,
то
по
г
р
афической
пов
ерхности
и
Т.д
..
Этот
этап
работы
похож
на
по
д
во
дну
ю
часть
айсберга,
ко
торую
обычно
не
видно,
но
размеры
ее
з
н
а
ч
ител
ьн
о
боль
ш
е
надво
дной
части.
После
·
ввода
и
корректировки
и
сх
о
д
но
й и н
фо
р
мации
прои
зводятся
ее
статистическая
обр
а
ботка.
Но
для
по
лучени
я к
о
рректных
р
езультатов
предварительно
следует
привести
вс
е
испо
ль
зуемые
в
расчета
х
пробы
к
одинаковой
длине
.
для
эт
ого
сущ
е
ст в
уют
стандартные
методы
расчетов.
В
ча
с
тности
в
системе
Д
атамайн
имеетс
я
3
специал
ьных
процесса
компо
з
ирования
.
2.2.
Описание
одной
переменной
Исходные
дан
н
ые
"
г
о во
р
ят
"
б о
лее
понятн
о,
когд
а
они
о
р
га
н
из
ованы
.
Когда
Вы
н
а ч
инаете
работать
с
каким-
т
о
масси
вом
информ
а
ции
,
с
аман
п
ервая
и
д
о
ступн
ая
информация
ПОЛ
УЧCiется
с
помощью
ги
с
тограммы
,
ко
то р
ан
как
правило
с
одер
жит
2
кривые:
частоты
от
д
ельных
кла
с с
о
в
соде
р
жаний
и
КУМУJlЯ1
'
ИВНОЙ
частоты.
На
рис
.
2.2
.
пока
за
на
г
ис
т
о
грамма
содержаний
золота
и
кумулятивный
график
часто
т
для
жильно
го
м
е с
то
р
ождения
.
20
0
...
1"'''
.
'''(
r I
с
Т
о
r
р
А
V
W.
А
I 3 •
,.
а
n
А
l!t~tS.C
Д
n
я
AU
~
гr==~~
~==~
I
~
а
•
·0
~
~
~~~;
.
~
1S
~=
:~:;!!~9~
: :
;~=
: ~ I
~C;j:~~~~=~=
~
~~=~;~
..
..
..
••
------------------~
Ри
с.
2.2
.
Ги
ст
огр
а
мм
а
с
о
д
ер
жания
золота
n
жильном
м
е
ст
оро
ждении
.

Следующая
важная
детал
ь
-
установить
по
гистограмме
тип
(
з
акон)
расп
р
еделенил,
что
поможет
В
ам
в
д
альнейшем
правильно
использовать
для
об
р
аботки
дан
н
ых
те
и
ли
ины
е
математические
выражения
и
методы
расчетов.
Самый
рас
пр
остраненный
в
ма
т
е
матике
тип
распределения
,
для
которого
су
щ
е
ст
вуют
н
а
и
б о
лее
простые
методы
расчета
НОРМАЛЬНОЕ
(
или
ГАУСС
ОВО
)
р
ас
пр
е
деление
,
рис
.
2.4
.
Важно
ть
этого
рас
п
реде
л
е
ни
я
с
тановит
с
я
'
понятной
в
связи
с
центральной
п
р
едельной
тео
р
е
м
ой,
которая
приводится
в
любом
учебнике
теор
и
вероятностей.
Пр
а
ктический
смысл
ее
состоит
в
том,
что
если
на
исследуемый
об
ъ
е
кт
во
зд
ействует
множество
факторов
,
то
числовые
характерист
и
ки
о
бъект
а
,
интерпретируемые
как
случайные
величин
ы
,
будyr
распределе
ны
примерно
·
нормально.
Математическая
Функцил
нормал
ь
ного
рас
пр
едел
ения
случайной
величины
Х
задается
равеНС1'ВОМ
(и-m)
2
P
{X~z}
=
~
f
Z
е
- 20 2 du ,
<1Щ
-
00
гд.е
т
,
(1
2
-
пар
а
м
е
тры
р
ас
пред
е
ления
.
(2.1)
Однако, для
вы
ч
и
сле
ния
вероятностей
нет
необходимости
применять
фо
р
мулу
2.
1,
Т.
К.
в
л
юбом
справочнике
по
статистике
и
тео
р
ии
вероят
ност
ей
прив
е
дены
подробные
таблицы
характеристик
но
р
маль
н
ого рас
пр
еделе
ния
.
Достаточно
простые
формулы
расчета
функци
и
но
р
мальног
о
рз
с
пр
едел
ен и
я
приведены
в
работе
[5].
Существуют
с
п
особ
ы
пр
еоб
разования
практически
любого
распределения
к
нормаль
но
му,
но
для
начала
полезно
знать
насколько
близко
Ваше
реальное
расп
р
еделен
и
е
к
Г
а
уссову.
Это
можно
сделать
или
с
п
ом
ощью
сПtщиальных
статистических
пакетов
программ
,
в
которых
пр
о
веря
ется
истинность
Вашей
гипотезы
о
но
р
мальности
распределения,
или
исп
ользуя
специальную
разграфленную
бумагу
(с
логариф
ми
че
с
к
им
масштабом
шкалы
У)
.
Оказы~ается,
что
если
Ваше
рас
пред
е
л
е
ни
е
близко
к
нормальному
,
то
кумулятивный
график н
а
тако
й
бу
м
аг
е
выгля
ди
т
почти
прямой
линией
.
Однако,
в
большинстве
случаев
р
еаль
н
ые
распределения
сильно
отличаются
от
нормал
ь
ного.
О
б
ы
чно
эт
о
случает
ся
,
ког
д
а
в
м
а
ссив
е
данных
встречаютсн
много
очен
ь
мален
ьких
значений
и
всег
о
несколько
очень
больших
(ил
и
наоборот)
.
В
э
том
случае
к
реальной
гистограмме
может
быть
подобра
н
л
огнормальный
закон
распределени
я,
при
котором
р
аспреде
л
ение
л
огарифмов
величи
н
массива
данных
является
нормапьн
ым
.
Обычно
этот
тип
расп
р
едел
е
н
ия
т
а
кже
ле
гко
распознается
с
помощью
кумулятивного
гра
ф
и
к
а
на
сп
е
циальной
бумаге
(аналогичн
о
показанному
выш
е
приме
р
у).
О
с
о
бен
но
много
трудностей
при
идентификации
lИШl
раслределенил
вно
сят
"
ур
аганные"
з
н
а
чения
проб
.
ЭТI1
пробы
желательно
привести
к
"
н
о
рм
ал
ьному"
виду
(и
з
в
е
стными
в
практике
методами)
или
искл
ю
ч
и
ть
д
л
я
получ
е
ния
бол
е
е
корр
е
ктных
ра
пределений
.
ушествует
мнение,
что
тот
эта
п
,
с
вя
за
н
ны
й
с
о
пр
еделе
ни
е
м
акон
а
распр
е
дел
е
ния
исследуемой
пе
р
еме
нной
,
не
д
ол
ж
е
н
в
об
щем
с
л у
чnе
Зi1
Н11МnТЬ
много
времени
.
Близость
~
а
ш
его
р
а
сп
ред
е
ле
н
ия
к
:l1
нормальному
не
гарантирует
эффективности
применяемого
метода
оценки.
С
другой
стороны
многие
методики,
основанные
на
гипотезе
нормального
закона
дают
хорошие
результаты
и
в
случае
негауссовых
распределений.
Только
небольшое
количество
методов
'
требуют
предварительной
идентификации
закона
распределения
.
Подробнее
этот
вопрос
рассматривается
в
главах
3
и
8 .
.
В
системе
ДАТ
АМЛЙ
Н
для подбора
закона
распределения
к
экспериментальной
гистограмме
используется
программа
HISFIT,
которая
позвоmiет
идентифицировать
нормальный
и
логнормальный
законы
распределения,
в
том
числе
и
многовершинные,
Рис.2.З.
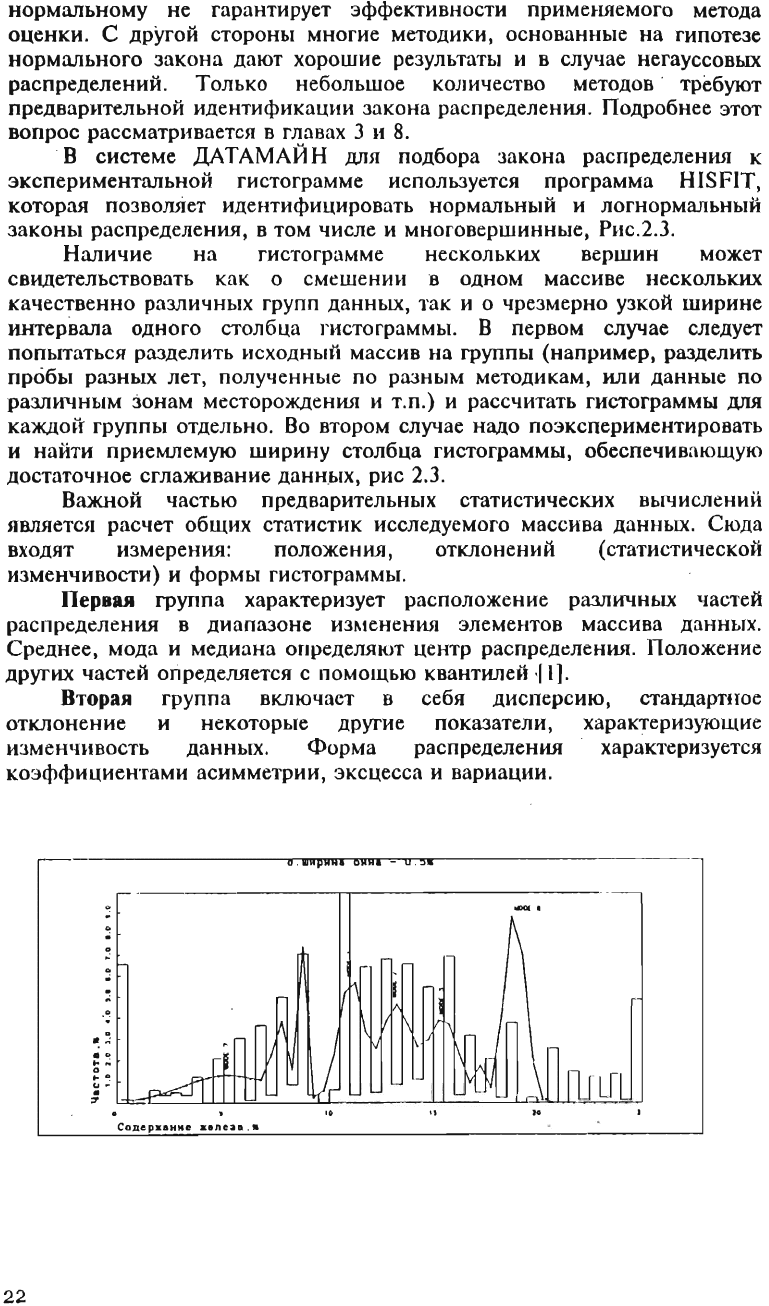
Наличие
на
гистограмме
нескольких
вершин
может
свидетельствовать
как
о
смешении
в
одном
массиве
нескольких
качественно
различных
групп
данных,
так
и
о
чрезмерно
узкой
ширине
интервала
одного
столбца
гистограммы.
В первом
случае
'
следует
попытаться
разделить
исходный
массив
на
группы
(например,
разделить
пробы
разных
лет,
полученные
по
разным
методикам,
или
данные
по
различным
зонам
меСТОРОЖдения
и
т.п.)
и
рассчитать
гистограммы
для
каждо~r
группы
отдельно
.
Во
втором
случае
надо
поэкспериментировать
и
найти
приемлемую
ширину
столбца
гистограммы,
обеспечив
ающую
достаточное
сглаживание
данн
.
ых,
рис
2.3.
Важной
частью
предварительных
статистических
вычислений
нвляеТСJl
расчет
общих
статистик
исследуемого
массива
данных.
Сюда
входят
измерения:
положения,
отклонений
(статистической
изменчивости)
и
формы
гистограммы.
Первая
группа
характеризует
расположение
различных
частей
распределения
·
в
диапазоне
изменения
элементов
массива
данных.
Среднее,
мода
и
медиана
определяют
центр
распред~ления.
Положение
других
частеЙ
определяется
с
помощью
квантилей
'
11].
Вторая
группа
включает
в
себя
дисперсию,
стандартное
отклонение
и
некоторые
другие
показатели,
характеризующие
изменчивость
данных.
Форма
распределения
'
характеризуется
коэффициентами
асимметрии,
эксцесса
и
вариации.
_ .
.
"
..
Содер
••
н"_
••
nе38
,
.
22

.
..
..
..
..
..
Содер
••
UII8
аеllСlе
,
1'
РIIС
.2
.
З
.
ГlIстограммы
сuдержаШtll
железа
D
пробах
и
зако
ны
распределеНИJl
при
ширине
бllна
0.5
11
2%
в
итоге
сумма
этих
парамстров
достаточно
полно
характери
з
ует
любое
ра~предеJlение.
2.1.1.
XapitKTepllcT8K~t
ПОJlож:еIIНИ
раСllределения
Среднее
(111)
-
это
арифмеl'll'IССКОС
среднее
данных
Вашего
массива.
__
~
, ,'.1 . ,
гn
-·
1; "-'
1=
1
Х
1
(2.2)
где
:
11
-
ЧИС1l0
Щ1ННЫХ
xi
-
11
J
НI'IИНЫ
данных.
Мсдюша
(Ме)
это
средняя
точка
ма
с
сива
AaIlHbIX
,
если
расположить
их
в
возрастающем
порядке.
Половина
данных
находнтсн
выше
медианы
,
а
другая
ПОЛОВИШI
-.
ниже.
М
е=
х
(
!!
i!.l )
(2.3)
если
1}
II
С
'l
сТllое
'шсло
,
и
2.4)
)(й
i)((
n
)
Мб
=
2 '2'+1
2
е
JIII
11
-
чеТНut:
ЧIIСJ\О.
Если
Ны
Ha'l
epT
IITC 1
умуля
ИDНЫЙ
график
на
специалыюй
бумаге,
то
медиаllУ
можно
ОllреДСlIИТL
11:
1
оси
Х,
указав
на
гр
..
фнк
е
T()'~KY,
СООТВСТСl'lIУIOШ,
уlO
частоте
50
%
на
OCII
У.
.
Мода
-
это
ВСШ1(шна
данных,
которая
нстре
чае
'
СН
в
массиве
наиболее
ча
то.
Обы'lНО
место
нахождеllИЯ
этой
.величины
сразу
61IДHO
на
ГИСТОГР:1мме
по
са
мому
вы
с
окому
столбику
.
Далее
надо
IIЮСТО
выя
с
нить,
какая
веЛИ'IИН3
данных
встречается
в
эт
ом
классе
нзиболее
часто.
n
геологической
практике
эта
е
татисти'
ескзя
xaV<tKTe
pl
'
тнка
не
играет
большой
роли
и
редко
ПРИМ~НJlеТСJl.
МИНИМ:lJ1ЫI<Ul
и
М3
с
им3лыl
яя
величины
д,
нн
IХ
:
но
наименьшее
11
наиболыш:е
з
Н\LJеню
tvШССИВ3
.
Нижний
и
ВСРХIIIIЙ
КRаРТIIЛI1
это
знu
'
е
)1ШI
массив
I
СООТ8
Т~IJУЮ
Щl1
е
25%
(нижний
.8
НТИJ1Ь)
И
75%
(вер
х
ний
кван
ИЛЬ)
'шстотам
на
К
УМ
УЛ>lТивном
граф
,ке
.
23

Кроме
названных,
существуют
и
другие
методы
разбиения
массива
на
части,
пока
широко
не
используемые
в
оте'[ественной
практике
2.
2.2.
Характеристики
отклонений
(с
т
аТlfСТllческой
изменчивости)
Дисперсия
0-2
=;}
L7:,
(Х;
-
т
)2
(2.5)
Этот
очеl1Ь
важный
параметр
определяет
квадрат
среднего
отклонения
величин
массива
данных
о
т
их
среднего
зна
чения.
Стандартное
отклонение
-
определяе
тся
как
Kop
ellb
квадратный
из
вели
!Ины
дисперсии.
Междукоартильное
простр:шство
(Днапп
:
юн)
-
полезный
параметр,
определяемый
из
уравнения
'ОЯ
=
О
з
-
О
1 (2.6)
Этот
параметр
не
использует
величины
среднего
(т)
и
поэтому
часто
применнетсSl,
когда
есть
сомнения
в
корректности
определения
ш.
Коэффициент
вариации
-определяется
делением
стандартного
отклонения
на
среднее
значение
массива
.
ЕСШI
Вы
получили
этот
параметр
больший
чем
1,
то
'
в
Вашем
мас
ине
есть
з
нач
е
ния,
сильно
отличающиеся
от
основной
Mt\CCbl
данных
.
Во
всех
СЛУLllliLX
желательно
разобраться
с
такими
значениями
перед
н
ачалом
оценки
.
CV=
~
(2.7)
Иногда
это
'
~
параметр
измеряют
в
проц
ентах,
умножап
ero
на
100.
В
качестве
оценок
разброса
выбор
ки
нередко
используются
нормиров,шные
отклонения
максимального
и
минимального
значений
от
среднего
арифметического,
причем
нормирование
состоит
в
делении
этих
разностей
на
среднеквадратичное
(стан
да
ртное)
отклонение.
Такие
оценки
имеют
преимущество
перед
размахом выборки,
т
.
к.
выражают
<;>тносительные
отклонения
и
позволяют
сравн
ивать
раЗJнtчные
8ыборки.
2.2.3.
Характеристики
формы
рас.
ред
елttlt
ОI
Коэффициенты
асимметрии
и
экс
цессп
иногда
нпзывают
характеристиками
формы
распреДсJl
IIIIJI.
Нулевое
ЗН<\'Iение
Коэффициента
асимме
тр
ии
означает,
'1
о
выборка
расположена
симмеТРИLIНО
относительно
среднего
а
рифметическо
о
,
как
это
характерно,
например,
для
НОРММЫlOго
заКОllа
Р'
СflР
деления,
рнс.2.4.
Ко
ффициент
асимметрии
характери
зу
ет
"скошенность"
гистограммы
.
Чем
выше
данный
КОЭффlf'l{иенl',
тем
ОЛhше
влияние
данных
с
очень
большими
или
очен!>
м
ал
ыми
·
Н:lчеIJШIМИ
величин.
ЕСЛII
IJ
Массиве
преобладают
очень
M
~UIble
значеlll1Н,
а
медиана
больше
чем
среднее,
то
коэффициент
-
отрицаТСJ1
t
В
.
В
ofip.
тно
м
при
мере
с
преоблманием
"хвоста"
otleHb
БОЛЬШIIХ
Зllач
ний
мы
ПОЛУ'JИМ
положительную
асимметрию.
24

РИС
.
2.4
.
Вид
функции
нормального
распределения
(А),
распределения
с
отрицат
ель
н
ой
асимметрией
(В)
и
с
отрицательным
эксцессом
(С).
КОЭффИЦl1
ент
экс
це
сса
служит
мерой
островершинности
распределения
по
сравн
ению
с
нормальным
законом.
У
нормального
распределею
,
Ul
эт
от
коэффициент
равен
нулю.
Положительное
значение
эксцесса
указывает
на
более
острую
вершину,
а
отрицательное
-
на
более
пологую
кривую,
рис
.2.4.
Более
подробное
описание
всех
названных
выше
параметров
можно
найти
в
любом
учебнике
по
статистике
или
теории
вероятностей
(1,2).
В
системе
ДАТАМЛЙН
имеются
процессы
SТЛТS,
STATSl
и
STIGX,
которые
позnолнют
очень
быстро
получить
все
вышеприведенные
ГlapaMeTpы
для
любой
переменной
в
массиве.
Программа
HISTOG
ПРI:ЩJ-ш
з
начена
для
ностроения
графнков
гистограмм
.
дЛЯ
быстрого
со
:
щания
диагр
а
мм
рассеяния
используется
процесс
QU
10
.
Выше
был
вкратце
описан
способ обр
ащения
с
массивом
данных,
в
котором
соде
ржи
тся
ОдН"
Ilеременная
.
Т
ак
им
образом
можно
получить
отделыlс:
хараиt:.рИСТИКИ
для
каждой
переменной
массива,
однако
часто
1
1РИХОД
И
.ТСSl
иметь
дело
с
множествами,
в
которых
содержатся
одновременно
несколько
хnрактернстик
проб,
например
содержания
р
азличных
компонентов.
В
этом
случае
необходимо
располага
ть
информаЦИеЙ
об
их
в
з
аимосвязи
и
взаимозаnисимости.
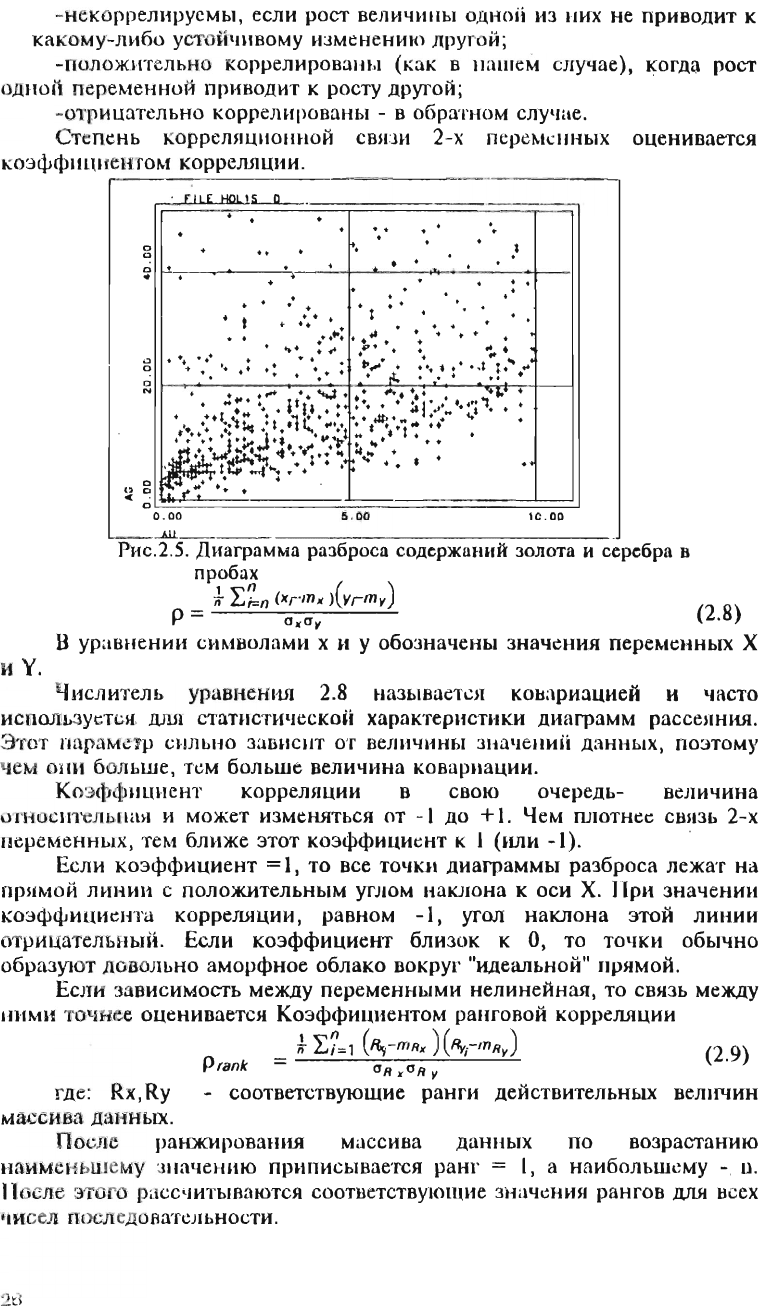
Наиболее
простой
путь
увидеть
взаИМОСВSIЗЬ
двух
ГlepeMeHHЫX
массива
-
построить
диаграмму
разброса,
аЮ\JlОГИЧНУIO
показанной
на
рис.2.5.
П
о
этому
гр
а
фику
можно
8
самом
общем
виде
сделать
заключение
о
СВЯЗII
2
-
х
персм
е
Ш/LГХ
.
Если
точк
и
концентрируются
вокруг
какой-то
линии,
то
можно
говори
ть
о
ДOCTaTO'iНO
над
ежно
й
связи
исследуемых
перемснных.
Однак
о
в
нашем
примере
хотя
и
существует
связь
меЖдУ
содержаНЮJМИ
золота и
серебра,
но
форма
этой
связи
на
диаграмме
расс
еяния
нвно
не
ви
д
на
.
Для
достаточно
точ
н
оii
оценки
степ
'ни
вззимосвя
з
и
перемеНВblХ
в
СТПТИСТИКе
11
по
люуетl.:Н
корреmщион
ный
анзлиз.
дв
переменные
Mor
'
yт
быть:
2В
-
некоррелируе
мы
,
е
сли
рост
величины
одной
и
з
них
не
приводит
к
какому-либо
устойчивому
и
з
м
е
нению
другой;
-положитель
но
коррелированы
(как
в
lI
а
ш
е
м
слу
чае),
KOГД~
рост
ОДНО
l1
переменнuй
приводит
к
росту
другой
;
-
отрицател
ьн
о
корр
ел
ированы
-
в
обра
т
ном
случае.
Степе
нь
корре
ляционной
СШIЗИ
2
-
х
п
е
р
е
м
е
нных
оценивается
коэффициентом
корреляции
.
и
У.
а
а
а
•
<>
о
о
...
а
~
о
. r
,Е
НOL
'L.It-
_
.
.
•
•
.
.
..
.
.
.
.
• .
+
.
.
.
.
.
•
..
.
t
•
"
.
......
;
.
.
...
...
..
+.
...+
+ •
•
:
..
....
t
..
. '
.:
.
'.
'
....
.:
...
:
..
~
i
t
++
~
••
..
••
1 +
...
+
..,.1
•••
+.-
.....
:.
t:'t..t
:*.'t'
.....
+.
w~~04
'J
........
:.'t.
. '
t
~
..... ,
+.:
, •
.'
.
~:f~
+.
..
.
• +
·
.
.
.
.
.
.
.
t
•
.
.
·
.
·
.
·
.
.
.
.
.
·
.
.
. .
.
f
·
·
.
.
.
.
..
~~
..
.
.
.
+
.
·
·
...
. .
·
.. ..
~~"i
........
"
..
"t
:.
...
..
..."
....
.
.:
h
••
:........
,
....
..
++
.....
f·
..
·
..
··+1
......
·tttt·
..
+.,..:
..
:"*
..
·*·t~+·
t
t
-.
....
....
'
...
....
$:
..
...
<>
0 .
00
S .
OO
1С
.
ОО
Ри
с.2.
5
.
Диаграмма
разброса
содержаний
золота
и
серебра
в
пробах
;}
L:
n
(/(
г
m
"
)(у
г
mу)
р
=
о
"
Оу
(2.8)
В
ур
а
внении
си
мволами
х
и
у
обозначены
значения
перем
е
нных
Х
Числитель
ура
внения
2.8
называ
етс
я
КОВ:1риацией
и
часто
используетсSl
для
С1
'
аТНС
'
Пf
1
1СС
I<ОЙ
характеристики
диаграмм
рассеяния
.
Этот
п
ара
Ме
Т
Р
сильно
зав и
с
нт
от
ВСЛИЧl1НЫ
зиа'Jений
данных,
по
эт
ому
че
м
ОIlИ
больше,
те
м
больше
величина
коварнации.
Ко
э
ффициент
коррешщии
В
свою
очередь-
величина
о
l
'
носи"елы
l1нH
и
может
изменяться
от
-1
до
+
1.
Чем
плотнее
СWIЗЬ
2
-
х
переменн
ы.х,
тем
бл
иже
этот
ко
э
ффици
е
н
т к
1
(юlИ
-1). .
Если
коэффи
циент
=
1,
то
все
TO'IKH
диаграммы
разброса
лежат
на
прямой
линии
с
положительным
углом
наклона
к
оси
Х.
При
значении
коэффици~нта
I<о
рреmщии,
равном
-
1,
угол
наклона
этой
линии
отрицательный.
Если
коэффициент
бли
з
ок
к
О,
то
точки
обычно
образуют
довольно
аморфное
облако
вокруг
"идеальной"
прямой
.
Если
зав
исимость
между
переменными
неJJИнейная
)
то
свя
з
ь
между
iШМИ
точнее
оценивается
Коэффициентом
ранговой
корреляции
;}
L7=1
(~
-
mя"
)
(
Яv
гm
яу)
Prank
=
0R
)(
OR
у
(2.9)
гд:
Rx)Ry
-
соответствующие
ранги
дей
ст
вительных
величин
массива
данных.
После
ра
н
ж
ир
о
вания
массива
да
нных
по
во
з
растанию
наименьшему
З
llачению
приписы
ваетс
я
ран}'
= 1,
а
н
а
иб
о
льш
е
му
-.
п
.
11
0
ле
э
того
рассч
итыв
а
ют
с
я
соотnеТСТВУlOщие
зна
ч
е
ния
рангов
для
I:Iсех
'
.и
сел
по
следо
патель
но
(,'Ти.
2
ТаБЛ.2
.
1
.
Матрица
коэффициентов
корреляции
,
м
ежду
показателями
опробования
месторождения.
Au
Ag
Cu
S
Р
Au
I
Ag
0.82
1
Cu
0.
17
0.53 1
S
-0.17
-0.27 -0.38
1
Р
-0.05 -0.08
-0.08 0.42
1
Прежде,
чем
переходить
к
установлению
вида
зависимост
ей
перем
ен
ных
Вашего
маССИ.Dа
желате1;lЬНО
рассчитать
матрицу
коэффициеитов
корреляции,
которая
укажет
тесноту
и
характер
связи
ра зли
чных
пока
ате
л ей
и
параметров.
Пример
такой
матрицы,
рассчи
та
нной
ДJU
l
резуль
тат
ов
опробования
комплексных
руд,
показан
в
таБЛ
.2.
1
.
2.3.1.
РегреССИОНIIЫЙ
анiUJИЗ
Регрессионный
анализ
-
это
метод
изучения
стохастической
свя
з
и
между
переменными.
Если
один
из
коэффициентов
корреляции
Р
,
авен
1
(или
-J),
то
все
точки
д
и
аг
р
а
ммы
рассеяния
лежат
на
одной
линии,
зная
уравнени
е
которой
мы
л
егк
о
мо
жем
вычислить
в е
JlИЧИ
'
ну
переменной
Х
по
известному
з
"
а~lеliИЮ
п
еремен
ной
У
и
наоборот.
Самый
простой
сл~шй
-
линейная
регр
есс
ия
,
когда
наша
искомая
лин.ш
-
прнман
с
уравнением
У
= дХ
+
Ь
, (2. 10)
где
:
а
-
УГJlОВОЙ
коэфф
ициент
равен
crv
д
=
р
а;
,
(2.11)
а
свобод
ный
член
у
равнения
Ь
равен
Ь
=
ту-дт
х
(2.12)
На
,
рис
2.6
показан
пример
по
дбо
ра
регрессионной
ПР$IМОЙ
для
с~шев:
FEOB=
f(FEM)
(левый
рису
нок
)
и
FEM=f(FEOB)
(прав
ыН
рисунок)
.
К
ак
видно
из
графиков
J1ИН
ИИ
этих
за
висимостей
отлич
аются
.
~~~~~
~~-_
.
_----
----~----~~
~
---------------
-------
-
-
--~
аграммы
разброса
и
регре
сс
ионные прямые
функций
FEOB=f(FEM)
(лев
ый
РIIСУНОК)
lf
FEM=f(FEOB)
(праоый
ри
сунок)
27

В
случаях,
когда
линия
не
прямая,
используются
более
сложные
нелинейные
уравнения
и
методы
регр
ессионного
анализа
.
для
подбора
аналитич
е
ских
функций
,
характеризующих
свизь
м
ежд
у
перемеНJ:IЫМИ,
чаще
всего
используется
метод
наименьших
квадратов
и
стандартные
вычислительные
процедуры,
описанные
в
каждом
.
учебнике
по
статистике
.
2.4.
Понятие
о
многомерном
статистическом
анализе
(11
в
предыдущи
х
разд
е
лах
мы
кратко
рассмотрели
анализ
данных
,
представляющих
измерения
одной
или
двух
переменных
в
каждой
пробе.
В
этой
части будет
дано
общее
представление
о
многомерных
методах
обрабо
тки
информации,
содержащей
несколько
или
много
переменных
для
каждой
.
пробы
или
объекта.
Такими
способ
ами
чаще
всего
оперируют
при
исследовании
результатов
геохимического
опробования
,
когда
для
каждого
образц
а
определяется
содержания
многих
элементов
и
химических
соединений,
при
анализе
палеонтологических
характеристик
и во
многих
других
ситуациях
в
геологической
практике.
Многомерные
методы
являются
необычайно
мощными
,
т.К.
позволяют
пользо
вателю
р
аботать
одновременно
с
большим
числом
переменных.
Однако
они
достаточно
сложны
и
требуют
обязательного
использования
ЭВМ.
Кроме
того,
статистичеСЮlе
критерии
и
процедуры
большинств
а
этих
методов
требуют
очень
серьезных
ограничений
,
поведение
которых
пока
еще
слабо
и
з
учено
.
Тем
не
менее
эти
методы
часто
позволяют
геологам
получать
большое
количество
полезной
инфоР.мации
и
делать
далеко
идущие
выводы
.
В
частности
они
полезны
там,
где
приходится
иметь
де
ло
со
сложными
ком
бинациями
действующих
факторов
,
которые
не
удается
и
з
учить
по
отдельности.
Во
'
мно
гих
стандартных
статистических
пакетах
компьютерных
программ,
а
также
в
специальном
геологич.еском
программном
обеспечении
есть
инструменты
ДIIЯ
таких
методов
анализа
.
В
частности
система
Датамайн
содержит
подсистему
(модуль)
,
включающую
все
упомянyrые
в
посл
едующем
изложении
методы.
Применительно
к
рассматрива
емым
в
данной
книге
геостатистич
ески
м
проблемам
методы
многомерного
анализа
используются
чащ
е
всего
ДIIЯ
разделения
исходной
информации
на
однородные
множества
,
которые
необходимо
исследовать
от
де
льно
.
С
этой
целью
обыч
но
используются
кла
сте
рный
и
дискр
иминан
тный
анализ.
2.4.1.
Множеств
енная
регрессия
Раньше
мы
рас
сматривали
регр
ессионный
анали
з
как
инструм
ент
для
подбора
аналитических
уравнений,
харак
теризую
щих
взаимозависимость
рассматрива
емых
переменных
.
В
это
м
случае
м
ы
имели
дел
о
ка к
пр
авило
с
одной
или
двумя
(для
тренда)
нез
висимыми
перем
е
нными
,
а
полиномиальную
регрессию
можно
было
представить
с
помощь
ю
уравнения
28

(2.13)
КоэФФиuиенты
Ь
в
этой
формуле
нахОДЯТСЯ
методом
наименьших
квадратов
с
помощью
решения
системы
линейных
уравнений.
Однако,
эту
же
задачу
можно
трактов
а
ть
как
многомерную,
содержащую
н
независимых
пер
менных.
В
этом
случае
мы
получим
уравнение
дтш
11
независи
ых
переменных
Х
У=ЬО+Ь,Х,
+Ь
2
Х
2
+ .....
+Ьпх
п
+Е,
(2.14)
которое
решается
анnлогично
пред
ыдущей
задаче
стандартными
методами
регр
ссионного
анаllиза.
В
результате
мы
получаем
уравнение
зависимости
искомой
переменной
от
нескольких
аргументов
и
сможем
оценить
их
влияние
на
кон
е
чную
величину
по
величине
коэффициеl
тон
Ь.
Стандартные
вь
числительные
процедуры
позволяют
при
этом
оценить
надежность
полученной
зависимости
по
Dеличине
коэффициента
множественной
корреляции.
2.4.2.
ДИСКРlIминаt
т"ый
анализ
в
отличи
е
от
методов
классификаци
и
(1,2]
дискрими:нантный
анализ
осуществляет
разделение
о
'ъект
ов
по
заранее
заданным
группам.
Например,
если
мы
име
ем
2
группы
проб,
связанных
с
различными
участками
месторож.ц
ния,
1'0
с
омощью
д
а
нного
метода
можно
отыскать
такую
линейную
функцию
переменных
,
с
помощью
которой
в
дальн~йшем
возможно
практичеСЮI
безошибочно
относить
полученные
новые
пробы
в
ту
ил
ИНУJ(1
груп
у.
Если
мы
имеем
в
составе
исходных
данных
информацию,
полученную
из
разных
источников,
по
-
различным
методикам
,
относящуюся
к
различным
участкам,
зонам
меСТОРОЖдения
и
Т.П.,
то
С
помощь
дискриминантного
анализа
мы
можем
проверить
значимость
этих
различий
в
данных.
Первым
сигнало
м
для
такои
работы
может
стать
получение
многовершинно
го
раСl1ределения
(гнст
гра1.
IbI)
дм
Ваших
данных.
Если
окажется
,
что
П
J.
том
8
массиве
имеются
различные
группы
информации
снеодинаковым
происхождением,
то
лучше
попробовать
вначале
ра
зделить
их
данным
методом
с
ом
ощью
соответствующей
программы
стандартного
статистичеСl
'ОГО
пакета
или
с
помощью
программ
DISCAN
и
DJSCLA,
имеющихся
в
системе
ДатамаЙн.
В
слу'ш
е,
если
указанные
Вами
ГР}1iПЫ
данных
можно
четко
разделить
на
отдельные
множества
с
помощью
полученной
дискримиltантной
функции
,
то
лучше
не
рисковат
и
в
дальнейшем
обрабатывать
эти
группы
данных
раздельно.
2.4.3.
КДС1стерный
анали
з
Этот
етод
многомерного
а
llализа
данных
относится
к
методам
классификации
и
выполняет
разделение
объектов
на
боле
или
менее
одноро
д
ны
е
группы,
а
также
устанавливает
соотношt:нин
между
:этими
груп
пами
.
В
литературе
описаны
сотни
методов
кластерного
анализа.
Многообразие
их
объясннется
эмпирич~
ким
подходом
к
образованию
2
