Капралов Е.Г., Кошкарев А.В., Тикунов В.С. и др. Геоинформатика

Подождите немного. Документ загружается.

ядер,

качестве

К-го

ядра выбирается

ОТЕ,

наиболее отличающа-

яся

от (АЧ)

ядер.

Другой принцип формирования ядер основывается

на

выделе-

нии максимально гомогенных классов ОТЕ.

При

выборе ядер клас-

сов необходимо, чтобы

при

отнесении

к ним

оставшихся

ОТЕ по

минимальности расстояния

(и

получении таким образом системы

классов) используемый функционал качества классификации

достигал своего экстремума (максимума

или

минимума,

зависи-

мости

от

интерпретации функционала качества).

Еще одним «ядерным» эвристическим алгоритмом является

метод последовательного выделения ядер.

основе этого метода

лежит предположение

о том, что

классы находятся друг

от

друга

на некотором расстоянии

с,

превышающем внутриклассовые рас-

стояния между

ОТЕ.

Алгоритм начинает свою работу

формиро-

вания первого ядра, которым становится

Далее,

на

каждом сле-

дующем шаге алгоритма рассматривается очередная

ОТЕ о,.

Если существует у-е ядро, расстояние

от

которого

до о,

меньше

порога

с,

О/

относится к у-му классу.

противном случае

о,

форми-

рует новый класс

становится

его

ядром.

Недостатками алгоритма являются: необходимость выбора

по-

рогового значения

с и

зависимость результатов

от

последователь-

ности поступлений

ОТЕ на

вход классификатора

(т.е. на

одном

том

же

наборе

ОТЕ

могут быть получены разные варианты класси-

фикации,

зависимости

от их

нумерации). Второй недостаток

яв-

ляется общим

для

всех последовательных процедур.

Метод k-средних. Метод ^-средних является одним

из

самых

известных параллельных оптимизационных алгоритмов класси-

фикации данных, основанных

на

описании классов ядрами. Идея

алгоритма заключается

постоянном пересчете ядер классов,

что

позволяет

процессе

его

работы выйти

на

реальную структуру сгу-

щений

ОТЕ в

признаковом пространстве.

формальной точки зре-

ния алгоритм минимизирует суммарный разброс

ОТЕ

вокруг ядер.

Несомненным преимуществом алгоритма является лучшее,

не-

жели

без

пересчета ядер классов, качество классификации, спо-

собность находить истинные ядра

скопления

ОТЕ в

признако-

вом пространстве. Недостаток алгоритма

—

большое количество

вычислений.

Параметрические методы классификации, основанные

на

модели

смеси распределений. Модель смеси распределений

наиболее про-

стом случае конечного числа классов

М и

однотипности компо-

нент записывается

виде

/о(*)

= 2>/А*.»Д (2.33)

/=|

где>о(х)

—

плотность генеральной совокупности;

—

число ком-

понент смеси;

р,

— вероятность появления

/-й

компоненты смеси;

/(х,

9/) — плотность /-й компоненты смеси; 9, — вектор парамет-

ров для /-й компоненты смеси (например, для одномерного нор-

мального распределения 9, = (ц,,а/)).

Модель смеси распределений применительно к задачам класси-

фикации подразумевает, что /-й класс полностью характеризуется

/-й компонентой смеси и вероятностью ее появления. Задача клас-

сификации ОТЕ состоит в определении, в рамках какого из клас-

сов появление данной ОТЕ наиболее вероятно.

Самым сложным этапом при классификации на основе модели

смеси распределений является процедура идентификации смеси,

т. е. алгоритм получения числа классов М и оценок для />, и 9,,

которые необходимы для построения решающего правила. Не все

смеси идентифицируемы, т.е. не для всех типов распределений

можно найти единственные оценки Л/, р,- и 9,. Например, смесь

нормальных распределений идентифицируема, а смесь равномер-

ных — нет.

Существуют различные подходы к оцениванию по множеству

ОТЕ параметров смеси, наиболее распространенным из которых

является ЕМ-алгоритм.

Название ЕМ-алгоритм происходит от сокращений англий-

ских терминов

Estimation

(оценивание) и

Maximization

(макси-

мизация).

Этот метод для фиксированного числа классов (элементов

смеси) К позволяет определять оценки параметров смеси p

и 9„

/ € {1,К} путем многократного нахождения очередных прибли-

жений к оценкам (шаг

Estimation)

и максимизации с учетом при-

ближений функции правдоподобия (шаг

Maximization).

Иерархические методы классификации. Иерархические методы

классификации нацелены либо на последовательное объединение

исходных ОТЕ в заранее заданное или незаданное меньшее коли-

чество классов, либо, наоборот, на расчленение одного или не-

скольких классов до нужной степени детализации. Процедуры пер-

вого типа носят название иерархических агломеративных алгорит-

мов классификации, второго — иерархических дивизимных алго-

ритмов классификации.

Исходной информацией для проведения иерархической клас-

сификации обычно служит матрица близостей вида ОТЕ-ОТЕ.

Исключением является, например, дивизимный алгоритм на ос-

нове метода 2-средних (т. е. метода ^-средних при к = 2).

Преимуществами иерархических алгоритмов являются возмож-

ности их применения без наличия априорной информации о свой-

ствах классов (например, ядер классов или обучающих выборок),

модификации для целей географического районирования, приме-

нения при неизвестном числе классов и наглядной визуализации

хода и результатов классификации на специальном графике, ко-

торый называется дендрограммой:

6 Геоинформатика

161

На оси х этого графика изображаются ОТЕ (в том порядке, в

котором они объединялись или разъединялись), по оси у — либо

шаг алгоритма, либо расстояние между вновь объединяемыми или

разделяемыми классами. Два объединяемых или разъединяемых

класса соединяются П-образной линией. Ее нижние концы упира-

ются в середины двух классов, а длины вертикальных отрезков

равны расстоянию между классами.

К недостаткам иерархических процедур следует отнести боль-

шую вычислительную стоимость их реализации. Данный недоста-

ток частично компенсируется существованием так называемых «бы-

стрых» (или «пороговых») иерархических алгоритмов.

Агломеративные алгоритмы. Классический агломеративный

алгоритм иерархической классификации начинает свою работу с

формирования К

= N классов (при этом каждая ОТЕ на нулевом

шаге представляет отдельный класс) и проводит в общем случае

1= N-

итерацию. На каждом шаге алгоритма происходит объеди-

нение двух «ближайших» классов в один, т.е. К„- 1 = Х^,. После-

дний (ЛМ)-й шаг алгоритма характеризуется объединением двух

сформированных на предыдущих этапах классов в один класс, вклю-

чающий в себя все имеющиеся (поступившие на вход анализа)

ОТЕ. Выбор расстояния настолько влияет на результат классифи-

кации, что зачастую оно вносится в название алгоритма (напри-

мер,

«агломеративный алгоритм средней связи»).

Если число классов К

которое нужно получить, известно зара-

нее,

достаточно провести /= N- К итераций, в результате которых

и будет сформировано ровно К классов. Если количество классов

заранее неизвестно, то анализируются либо значения функциона-

ла качества разбиения для К е

{2,А^},

либо применяются

другие методы (см., например, метод анализа сложности группи-

ровочного дерева в работе В. И. Блануца, 1993. — С. 94). Информа-

цию о количестве классов может дать и визуальный анализ денд-

рограммы.

Необходимо отметить существование так называемых «быстрых»

агломеративных алгоритмов. Они основаны на использовании не-

которой заранее задаваемой или настраиваемой в процессе клас-

сификации последовательности пороговых значений с

(при

этом вполне возможно, что с, = с =

const

V/i е

{1,/}).

На очередной итерации алгоритма л е{1,...,/} объединяются

те классы, расстояния между которыми не превышают заданного

порога с,-. Таким образом, на каждом шаге не требуется искать ми-

нимальный элемент в матрице расстояний. При верном выборе

пороговых значений такой подход повышает скорость работы ал-

горитма без потери качества классификации.

Детальное описание процедур агломеративных иерархических

классификаций можно найти в работе [М.Жамбю,

1989].

Дивтимный алгоритм. Дивизимный алгоритм иерархической

классификации начинает свою работу с формирования единствен-

ного класса, содержащего все ОТЕ, и проводит в общем случае / =

N-1 итерацию. На каждом шаге алгоритма происходит последо-

вательное разделение одного из классов на два таким образом,

чтобы качество получаемой классификации было максимальным.

Последний шаг работы алгоритма делит единственный оставший-

ся нерасчлененный класс, состоящий из двух ОТЕ, на два класса

(по одной ОТЕ в каждом).

Дивтимный алгоритм на основе расчленения графа близостей.

Дивизимный алгоритм расчленения графа, по аналогии с «быст-

рым» агломеративным алгоритмом, требует задания последователь-

ности пороговых значений с

На каждой итерации алгорит-

ма п е {1,/} происходит исключение из графа ребер с больши-

ми значениями, после чего проверяется, на сколько подграфов

(компонент связности) распался исходный граф. Каждый подграф

представляет собой отдельный класс.

Методы районирования. Алгоритмы формального районирова-

ния направлены на получение территориально нерасчлененных рай-

онов,

выделяемых по критерию их несхожести в признаковом про-

странстве с учетом выбранной метрики или матрицы близостей ОТЕ-

ОТЕ. Районирование является классической задачей географии, где

оно выполняется по логическим правилам и кроме признака несхо-

жести и территориальной нерасчлененности районов зачастую, как,

например, в социально-экономической географии, требуется до-

полнительно наличие ядра районообразования, районообразующих

связей и др. Ряд алгоритмов формального районирования, с одной

стороны, практически полностью дублирует алгоритмы классифи-

кации с добавлением дополнительной процедуры проверки усло-

вия на наличие смежности у объединяемых в районы территориаль-

ных единиц. С другой стороны, существуют специфические алго-

ритмы районирования, для которых отсутствуют аналоги в класси-

фикации (например, метод барьеров максимальных различий, клас-

сические примеры физико-географического районирования).

Для систематизации методов районирования, по аналогии с

обычными классификациями, используют несколько оснований.

По сфере применения выделяют природное и социаль-

но-экономическое районирование. Именно в Этих сферах важна

территориальная нерасчлененность районов. Природные признаки

априорно распределены непрерывно по территории, а социально-

экономическая география является основой территориального уп-

равления.

По интерпретации расстояний между объекта-

ми в пространстве признаков многие авторы выделяют узловое и

однородное районирование. Узловое районирование позволяет

формировать районы на основе силы связей между ОТЕ, однород-

ное — на основе «похожести» значений их показателей. С содержа-

тельной точки зрения это разные группы методов. С математической

точки зрения разница между ними сводится только к различию спо-

собов выбора метрики и функционалов расстояний и качества.

По степени охвата районирование можно подразделить

на интегральное и отраслевое [В. И. Блануца, 1993. — С. 3]. Напри-

мер,

в случае экологического интегрального районирования оце-

нивается экологическая ситуация в целом, а в случае отраслевого

экологического районирования — какой-либо аспект экологичес-

кой ситуации (состояние воздушной среды, почв, растительного

покрова и т.д.). Отраслевое районирование отличается от интег-

рального только подбором признаков и способом их предвари-

тельной обработки.

По динамике изменения характеристик классов

О Т Е в одном из пространств методы районирования подразделя-

ются на нацеленные на выявление районов с разными трендами

атрибутивных признаков и на определение тенденции изменения

сетки районов.

Методы районирования, основанные на описании районов ядра-

ми.

Основной проблемой этого класса методов является выбор ядер

районов, которые обязаны быть реальными ОТЕ. После того как

ядра районообразования получены, начинается последовательное

присоединение к ним максимально «похожих» смежных ОТЕ.

В экологических и географических исследованиях часто приме-

няют для районирования стандартные методы классификации, а

после получения классов анализируют их пространственную струк-

туру. Затем, выделив в каждом классе несколько ОТЕ, образующих

пространственно-целостный район, полагают их ядрами районов.

После этого выделенные ядра расширяются путем доклассифика-

ции оставшихся ОТЕ по приведенному выше алгоритму.

Методы районирования, основанные на модели смеси распреде-

лений. Параметрические методы классификации на основе модели

смеси распределений играют важнейшую роль в прикладной ста-

тистике. На основе этих методов разработаны эффективные алго-

ритмы, которые могут применяться для классификации и эколо-

гических, и географических данных.

В работе

[C.Ambroise,

G.Govaert,

1996]

описана модификация

ЕМ-алгоритма, которую авторы назвали NEM-алгоритмом

(Neighborhood

ЕМ-алгоритм). Этот метод позволяет учитывать

по-

мимо атрибутивного признакового пространства

любое другое

пространство, заданное матрицей близостей ОТЕ-ОТЕ.

данном

случае дополнительным пространством будет географическое,

матрица близостей может быть

как

бинарной таблицей смежно-

сти,

так и

заданной пространственными расстояниями между

па-

рами

ОТЕ.

По аналогии

ЕМ-алгоритмом, NEM-алгоритм итерационно

находит оценки всех параметров,

на

каждом шаге улучшая их. Оцен-

ки апостериорных вероятностей

{

используются

для

райониро-

вания

(или

нечеткого районирования) точно

так же, как и в

клас-

сическом ЕМ-алгоритме. Недостатком алгоритма является необхо-

димость подбора параметра веса пространства,

от

значений кото-

рого сильно зависит результат районирования.

Иерархические методы районирования. Отличие агломеративных

алгоритмов районирования

от

соответствующих алгоритмов клас-

сификации состоит

формировании матрицы пространственной

смежности

проверке

на

каждом шаге граничности объединяе-

мых районов.

При

этом классические агломеративные алгоритмы

классификации можно использовать

для

районирования

при

усло-

вии,

что

минимум расстояния между районами

(или

максимум

функции качества

при

объединении) ищется только

для

простран-

ственно-смежных районов.

Быстрый агломеративный алгоритм районирования полностью

соответствует быстрому агломеративному алгоритму классифика-

ции

добавлением этапа проверки

на

шаге

граничности объеди-

няемых районов, расстояния между которыми

признаковом про-

странстве меньше константы

с„.

Большинство дивизимных алгоритмов районирования,

по

ана-

логии

«ядерными»

агломеративными, получается путем есте-

ственной модификации классических методов классификации.

Дивизимному алгоритму классификации, основанному

на

методе

2-средних, соответствует полностью повторяющий

его

метод рай-

онирования

на

основе алгоритма 2-медондов. Дивизимному алго-

ритму, основанному

на

расчленении графа, соответствует давно

описанный

стандартной литературе

по

прикладной статистике

[С.А.Айвазян

и др., 1989]

метод классификации

при

ограничени-

ях. Ограничения накладываются

на

используемую

дивизимном

алгоритме матрицу близостей

признакового пространства мат-

рицей пространственной смежности

G в

соответствии

форму-

лой

Это условие соответствует удалению

из

графа расстояний при-

знакового атрибутивного пространства (соответствующего матри-

це А) ребер, соединяющих пространственно несмежные ОТЕ. После

удаления ребер

полученному графу применяют дивизимный

ал-

горитм

на

основе расчленения графа, описанный выше.

Помимо стандартных методов разработаны

широко использу-

ются специализированные

для

экологии

географии процедуры

районирования,

для

которых отсутствуют аналоги

классифика-

ции. Речь

первую очередь идет

методе барьеров максимальных

различий, предложенном М.С.Монмонье

[M.S.Monmonier,

1973].

Этот метод применим только

к ОТЕ

полигонального типа.

Значением барьера

для

заданного района (содержащего более

одной ОТЕ) будем называть максимальное расстояние между дву-

мя пространственно смежными

ОТЕ

этого района

пространстве

показателей, барьером

—

границу между двумя соответствующи-

ми ОТЕ. Обозначать значение барьера /-го района будем символом

B(S

B(S,)

= max {d(o

tX9

)

iX9

g(o

iX9

) =

1}.

(2.35)

Для районирования методом барьеров максимальных различий

вычисляются расстояния только между пространственно смежны-

ми

ОТЕ, а все ОТЕ при

инициализации алгоритма относятся

одному единственному району. После этого

на

каждом шаге про-

исходит деление одного

из

полученных районов

на два

(необяза-

тельно равных

по

площади) района. Начинается деление

опреде-

ления

каждом

из уже

полученных районов

по

одному значению

барьеров, среди которых отыскивается максимальный. Район, име-

ющий

своем составе барьер

максимальным значением, подле-

жит делению.

По обе

стороны

от

барьера итеративно проводится

граница —

до тех

пор, пока

она не

разделит текущий район. Оче-

редная итерация расширяет границу

за

счет присоединения следу-

ющего барьера (который вычисляется

без

учета

пар

ОТЕ,

уже по-

участвовавших

образовании предыдущих барьеров), примыкаю-

щего

границе.

Можно ограничить количество итераций алгоритма, либо зара-

нее задавая искомое число классов

либо вводя некоторый

по-

рог с. Поскольку значения барьера максимальных различий умень-

шаются

каждым шагом алгоритма, критерием остановки алго-

ритма является условие

B(S])

= max

{ОД)

€ 1,п) < с, j е

{1,п).

Большое разнообразие примеров

методик классификации

экологии

географии, среди которых типологические, оценоч-

ные

комплексные классификации, классификации «нечетких»

систем, проблемы взвешивания показателей, оценка надежности

классификаций

другие можно найти

книге

[В.

С. Тикунов,

1997].

Контрольные вопросы

Какие методы расчета расстояний применяют в географии?

2. Охарактеризуйте показатели качества классификаций.

3. В чем различие оценочных и типологических классификаций?

4. В чем различие методов контролируемой и неконтролируемой клас-

сификации?

5. В чем смысл «нечетких» классификаций?

6. Для чего нужны нормировки показателей?

7. Что позволяет улучшить «взвешивание» показателей?

8. Охарактеризуйте методы классификации, основанные на описании

классов ядрами.

9. Опишите смысл параметрических методов классификации, осно-

ванных на моделях смеси распределений.

10. Охарактеризуйте иерархические методы классификации.

11.

Перечислите основные методы, применяемые для районирования.

2.2.3. Цифровое моделирование рельефа

Цифровое моделирование рельефа как одна из важных модели-

рующих функций геоинформационных систем включает две груп-

пы операций, первая из которых обслуживает решение задач со-

здания модели рельефа, вторая — ее использование.

Под цифровой моделью рельефа (ЦМР) принято понимать сред-

ство цифрового представления трехмерных пространственных объек-

тов (поверхностей или рельефов) в виде трехмерных данных, обра-

зующих множество высотных отметок (отметок глубин) и иных зна-

чений аппликат (координаты Z) в узлах регулярной или нерегуляр-

ной сети или совокупность записей горизонталей (изогипс, изобат)

или иных изолиний.

Первые эксперименты по созданию ЦМР относятся к самым

ранним этапам развития геоинформатики и автоматизированной

картографии первой половины 60-х годов XX в. С тех пор разрабо-

таны методы и алгоритмы решения различных задач, созданы про-

граммные средства моделирования, крупные, в том числе нацио-

нальные и глобальные, массивы данных о рельефе, накоплен опыт

решения с их помощью разнообразных научных и прикладных за-

дач.

Создание ЦМР. В проблематику создания ЦМР традиционно

входят вопросы оценки источников данных о рельефе (в том числе

их точности), выбора моделей пространственных данных для его

описания, методы реализации модели применительно к решае-

мой задаче, верификация полученной модели.

Источники данных для ЦМР. Несмотря на кажущуюся простоту

моделируемого объекта — рельефа, хорошо, на первый взгляд,

описываемого математически как поверхность или поле, практика

предлагает множество способов и технологий создания ЦМР

(рис.

17).

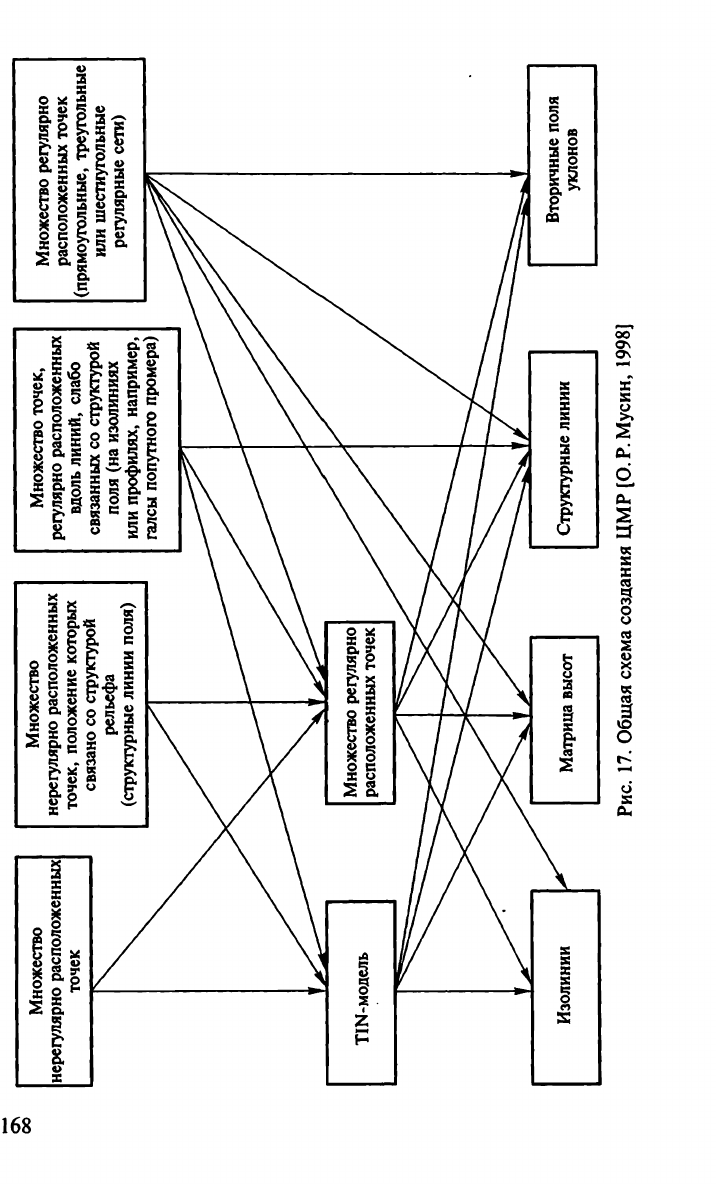
Множественность типов источников исходных данных о релье-

фе вызвана, в свою очередь, многообразием способов получения

и организации первичных измерительных сведений и их производ-

ных. Среди них геодезические работы и топографическая съемка

местности, стереофотограмметрическая обработка фототеодолит-

ных, аэро- и космических снимков, альтиметрическая съемка (ре-

льеф суши), промерные работы и эхолотирование подводного ре-

льефа акваторий океанов и внутренних водоемов, радиолокацион-

ная съемка рельефа ледникового ложа и небесных тел. Разнообраз-

ны и вторичные источники сведений о рельефе, например топо-

графические карты и планы, роль которых будет подробно изло-

жена ниже.

Пространственная организация исходных данных о рельефе как

множестве опорных точек модели (точек с известными высотны-

ми отметками) также различна. Их распределение может быть ре-

гулярным, структурным и хаотическим. С учетом технологии полу-

чения и предобработки (характера фотограмметрической обработ-

ки стереомоделей и технологии цифрования карт) можно выде-

лить системы высотных отметок рельефа в случайно расположен-

ных точках — узлах нерегулярной сети (получаемых, например, в

результате тахеометрической съемки), в частично упорядоченных

множествах точек (инженерные изыскания, эхолотирование), в

узлах регулярных решеток (специальные виды площадного ниве-

лирования, цифровая фотограмметрическая обработка, предвари-

тельная обработка других моделей), линейно упорядоченные мно-

жества точек, получаемые путем цифрования карт (обводом ли-

ний или сканированием), полностью или частично упорядочен-

ные множества точек, генерируемые в процессе фотограмметри-

ческой обработки стереомоделей местности. На рис. 17 выделены

четыре типа исходных множеств:

1) нерегулярно расположенных точек;

2) нерегулярно расположенных точек, положение которых свя-

зано со структурой рельефа (структурные линии поля);

3) точек, регулярно расположенных вдоль линий, слабо свя-

занных со структурой поля (на изолиниях или профилях, напри-

мер галсы попутного промера);

4) регулярно расположенных точек (прямоугольные, треуголь-

ные или шестиугольные регулярные сети).

Карта как источник массовых данных для ЦМР. Среди пере-

численного выше разнообразия источников данных для моделиро-

вания рельефа двум из них — картам и аэрокосмическим матери-

алам — принадлежит особая роль массовых источников.

В отношении данных дистанционного зондирования — матери-

алов аэро- и космосъемок, которые детально будут рассмотрены в

соответствующем подразделе, — заметим лишь, что их роль по раз-

ным причинам будет расти, а доля и роль карты — снижаться. Это