Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book

Подождите немного. Документ загружается.

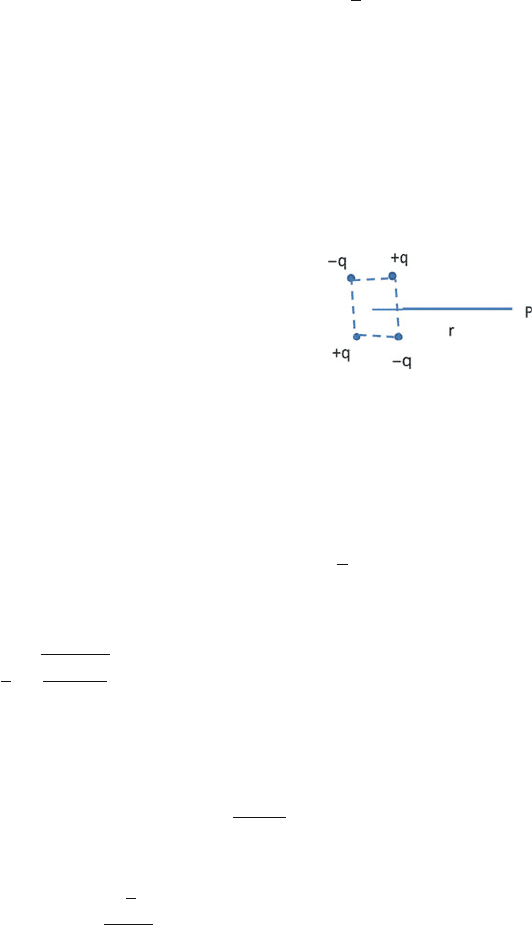
11.2 Problems 469

11.25 A thin non-conducting rod is bent to form an arc of a circle of radius r and

subtends an angle θ

at the centre of the circle. If a total charge q is spread

uniformly along the rod, ﬁnd the electric ﬁeld at the centre of the circle.

11.26 A ring of radius r located in the xy-plane is given a total charge Q = 2πRλ.

Show that E is maximum when the distance z = r/

√

11.27 A total charge q is spread uniformly over the inner surface of a non-

conducting hemispherical cup of inner radius a. Calculate (a) the electric

ﬁeld and (b) the electric potential at the centre of the hemisphere.

11.28 The quadrupole consists of four charges q, q, −q, −q located at the corners

of a square on side a (Fig. 11.4). Show that at a point p, distant r from the

centre of the charges and in the same plane, the electric ﬁeld varies inversely

as the fourth power of r, where r >> a.

Fig. 11.4

11.29 Show that the electrical and gravitational force between two bodies each of

mass m and charge q will be equal at any distance r if the ratio q/m =

8.6 × 10

−10

C/kg.

11.30 Two small, equally charged spheres, each of mass m, are suspended from the

same point by silk threads of length L. Initially, the spheres are separated

by distance x << L. As the charge leaks out at the rate dq/dt, the spheres

approach each other with relative velocity v = a/

√

x, where a is a constant.

Find the rate at which charge leaks out.

Show that

dq/dt =



2πε

11.31 A charge q is uniformly distributed over a thin ring of radius R. A very long

uniformly charged thread with linear charge density λ is placed on the axis

of the ring with one end coinciding with the centre of the ring. Show that the

force of interaction F will be equal to

qλ

4πε

11.32 A very long wire with uniform charge density λ is placed along the x-axis

with one end of the thread coinciding with the origin. Show that the electric

ﬁeld is given by E =

√

2λ

4πε

at 45

◦

with the x-axis at a distance y from the

end of the thread.

470 11 Electrostatics

11.33 If the electric potential is given by ϕ = cxy, calculate the electric ﬁeld.

11.34 Charges Q and −2Q are placed at a ﬁxed distance of separation. Show that

the locus of points in the plane of charges, where the potential is zero, will

be a circle.

[Indian Administrative Services]

11.35 Two identical thin rings, each of radius R, are coaxially placed a distance R

apart. If Q

and Q

are, respectively, the charges uniformly spread on the

two rings, ﬁnd the work done in moving a charge q from the centre of one

ring to that of the other.

[Indian Institute of Technology 1992]

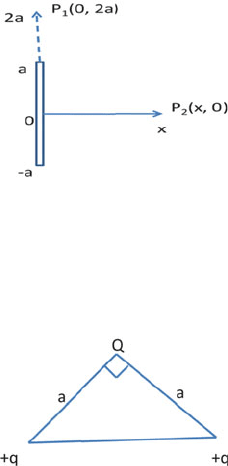
11.36 A thin rod of length 2a is placed along the y-axis in the xy-plane. The rod

carries a charge density λ (Fig. 11.5). The point P

is located at (0, 2a) and

at (x,0).

(a) Find x if the potentials at P

and P

are equal.

(b) Find the corresponding potential.

Fig. 11.5

11.37 Three charges +q, +q and Q are located at the vertices of a right-angled

isosceles triangle, Fig. 11.6. If the total i nteraction energy is zero what should

be the value of Q?

Fig. 11.6

11.38 Four charges each of magnitude q are located at the four corners of a square

of side a such that like charges occupy the corners across the diagonals

(Fig. 11.7). Calculate the work done in assembling these charges.

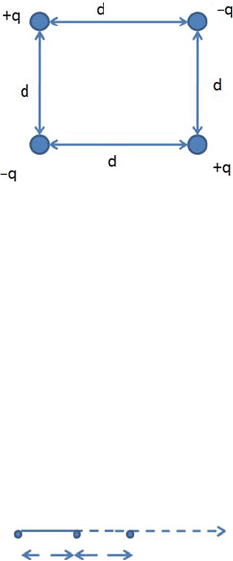
11.2 Problems 471

Fig. 11.7

11.39 Calculate the total potential energy of sphere of radius R carrying a uni-

formly distributed charge q.

11.40 A linear quadrupole (Fig. 11.8) consists of charge +2Q at the origin and two

charges −Q at (−d, 0) and (+d,0).

(i) Write down the magnitude of the electric ﬁeld at P on the x-axis where

x > d.

(ii) If x >> d show that the ﬁeld varies inversely as the fourth power of

distance from the origin.

(iii) If Q = 2 μC and d = 0.01 mm, calculate the ﬁeld at x = 20 cm.

Fig. 11.8 Linear quadrupole

−Q

+2Q

11.41 (a) If the breakdown ﬁeld strength of air is 5×10

V/m how much charge can

be placed on a sphere of radius 1 mm? (b) What would be the corresponding

electrical potential?

11.42 An electron is released from a distance 120 cm from a stationary point charge

+2 × 10

−9

C. Calculate the speed of the electron when it is 18 cm from the

point charge.

11.43 Figure 11.8 shows the linear quadrupole. Show that the electric potential

V (r) at a distance r >> d from the central charge and in a direction normal

to the axis of the quadrupole varies inversely as the third power of r.

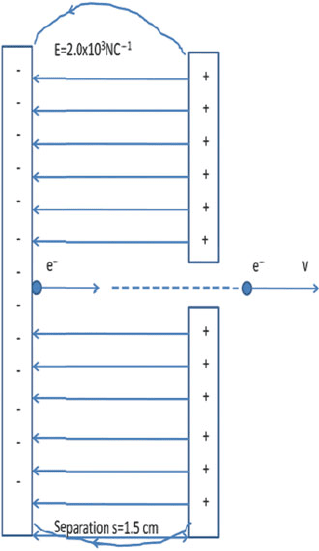
11.44 An electron of mass m

= 9.1 × 10

−31

kg is accelerated in the uniform

electric ﬁeld E between two parallel charged plates, as shown in Fig. 11.9.

There is no electric ﬁeld outside of the plates. The electric ﬁeld has a mag-

nitude E = 2.0 × 10

N/C and electron charge e =−1.6 × 10

−19

C. The

separation of the plates is 1.5 cm and the electron is accelerated from rest

near the negative plate and passes through a tiny hole in the positive plate.

Assume the hole is so small that it does not affect the uniform ﬁeld between

the plates.

472 11 Electrostatics

(i) What is the force on the electron while it is between the plates?

(ii) What is its acceleration and with what speed does it leave the hole?

(iii) What is the force on the electron outside of the plates?

[University of Aberystwyth, Wales 2005]

11.45 What is the electric potential V at a distance r from a point charge Q? Write

down an expression describing the electric potential due to a continuous

charge distribution.

Consider a disk of radius R which carries a uniform surface charge distri-

bution.

(a) Find the total charge on the disc.

(b) Find the potential at a point on the axis of the disc lying at a distance x

from the disc.

Comment on your result.

Fig. 11.9

11.46 In the Bohr’s hydrogen atom model, show that the orbital motion of the elec-

tron obeys Kepler’s third law of motion, that is, T

∝ r

11.2 Problems 473

11.47 Equal charges (Q) are placed at the four corners of a square of side a.

Show that the force on any charge due to the other three charges is given

by 1.914 Q

/4πε

11.48

(a) Calculate the electric ﬁeld due to a dipole on its perpendicular bisector.

(b) Show that for the distance x >> d/2, where d is the distance between

the charges, the ﬁeld varies inversely as the cube of distance.

−30

cm. Calculate the differ-

ence in potential energy when the dipole is placed parallel to the electric

ﬁeld of 3 ×10

V/m and then antiparallel to the ﬁeld.

11.2.2 Gauss’ Law

11.49

(a) State Gauss’ law of electrostatics i n mathematical form.

(b) Use Gauss’ law to show that the electric ﬁeld magnitude due to an inﬁ-

nite sheet of charge, carrying a surface density σ , is given by

E =

2ε

−8

C. It hangs

by a silk thread attached to a vertical uniformly charged sheet such that,

under the inﬂuence of both gravity and the electric force, it makes an

angle of 10

◦

with the sheet. Calculate the surface charge density of the

sheet.

11.50

(a) State Gauss’ law in differential and integral form.

(b) Show that the electric ﬁeld outside a charged sphere is Q/4πε

, where

r is the distance from the centre of the ball.

total charge Q and radius R,isQr/4πε

11.51 In prob. (11.50) the central part of the sphere is hollowed by creating a cavity

of radius

R concentric with the original sphere. If the charge density of the

hollowed sphere remains unchanged show that the electric ﬁeld at the surface

is now 7/8 of the original value on the surface.

11.52 In prob. (11.50) show that the electric potential (a) varies as that to simple

harmonic motion for r < R.(b)V (0) =

V (R) where V (∞) = 0.

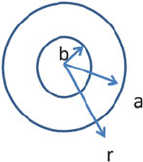
11.53 Figure 11.10 shows a non-conducting hollow sphere with inner radius b and

outer radius a. A total charge Q is uniformly distributed in the material b <

r < a. Find the electric ﬁeld for (a) r < b;(b)b < r < a;(c)r > a.

11.54 A charge Q is uniformly distributed in a long cylinder of radius R and charge

density ρ. Find the electric ﬁeld for the regions (a) r > R;(b)r < R.

474 11 Electrostatics

Fig. 11.10

11.55

(a) The electric ﬁeld on the surface of a thin spherical shell of radius 0.5 m

is measured to be 800 N/C and points radially towards the centre of the

sphere. What is the net charge within the sphere’s surface?

(b) An electric ﬁeld of 120 N/C points down over a football ﬁeld. Calculate

the surface charge density on the ﬁeld.

11.56

(a) Using Gauss’ law derive Coulomb’s formula for the electric ﬁeld due to

an isolated point charge q.

(b) A positive charge Q is uniformly distributed in a non-conducting sphere

of radius R. Calculate the electric ﬂux passing through the spherical

surface of radius r concentric with the sphere for (i) r < R; (ii) r > R.

11.57 How is electric ﬂux related to the electric ﬁeld E? How is the total electric

ﬂux over a closed surface related to the charge enclosed within the surface?

A thin spherical shell of radius R

carries a total charge Q

that is uni-

formly distributed on its surface. A second, larger concentric thin shell of

radius R

carries a charge Q

also uniformly distributed over the surface of

the shell. Use Gauss’ law to ﬁnd the electric ﬁeld in the regions.

(a) r < R

(b) R

< r < R

, and

< r.

The electric charges are such that Q

> 0 and the electric ﬁeld is zero for

r > R

. Find the ratio Q

11.58 Two insulated spheres of radii 1 and 3 cm at a considerable distance apart are

each charged positively with 3 × 10

−8

C. They are brought into contact and

separated by the same distance as before. Compare the forces of repulsion

before and after contact.

[Northern Universities of UK]

11.59 What is the maximum charge that can be given to a sphere of diameter 10 cm

if the breakdown voltage of air is 2 × 10

V/cm.

11.60

(a) Show that the capacitance, C, of a conducting sphere of radius a is given

by C = 4πε

(b) Two isolated conducting spheres, both of radius a, initially carry charges

of q

and q

and are held far apart. The spheres are connected together

by a conducting wire until equilibrium is reached, whereupon the wire

11.2 Problems 475

is removed. Show that the t otal electrostatic energy stored in the spheres

decreases by an amount U, given by

U =

16πε

−q

)

What happens to this energy?

11.61 Two spherical conductors of radii R

and R

and charges Q

and Q

, respec-

tively, are brought in contact and separated. Show that their charge densities

will be inversely proportional to their radii.

11.62 A light spherical balloon is made of conducting material. It is suggested that

it could be kept spherical simply by connecting it to a high-voltage source.

The balloon has a diameter of 100 mm.

(a) What is the voltage of the source if the electric ﬁeld on the balloon sur-

face is 5 × 10

V/m?

(b) What gas pressure inside the balloon would produce the same effect?

age. Calculate the total electrostatic energy of the balloon.

11.63 A soap bubble of radius R

is given a charge q. Due to mutual repulsion

of the surface charges the radius is increased to R

, the pressure remaining

constant. Show that the charge is given by

q =





+ R





1/2

11.64 An insulating spherical shell of inner radius r

and outer radius r

is charged

so that its volume charge density is given by

ρ(r) = 0for0≤ r ≤ r

ρ(r) =

for r

≤ r ≤ r

ρ(r) = 0forr > r

where A is a constant and r is the radial distance from the centre of the shell.

Find the electric ﬁeld due to the shell throughout all space.

11.65

(a) Show that electrostatic ﬁeld is conservative.

(b) An isolated soap bubble of radius 1 cm is at a potential of 10 V (assume

the bubble material is a conductor); calculate the total charge on the

bubble. If it collapses to a drop of radius 1 mm (no charge loss or gain

during the process), what is the change of the electrostatic energy of the

system?

[University of Aberystwyth, Wales 2008]

476 11 Electrostatics

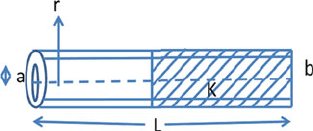
11.66 A long cylinder of charge q has a radius a. The charge density within its

volume, ρ, is uniform (Fig. 11.11). Describe the form of the electric ﬁeld

generated by the cylinder. Find the electric ﬁeld strength at a distance r from

the axis of the cylinder in the regions (i) r > a and (ii) 0 < r < a.

If a non-relativistic electron moves in a circle at a constant distance R from

the axis of the cylinder, where R > a, ﬁnd an expression for its speed.

[University of Manchester 2006]

Fig. 11.11

11.67 Consider an isolated non-conducting sheet with charge density σ . The elec-

tric ﬁeld at 25 cm from the sheet is found to be 200 V/m, directed towards the

sheet. Calculate σ on the sheet. What electric ﬁeld is expected at 2 cm from

its surface? How are the values of σ and E changed if a conducting sheet is

substituted.

11.2.3 Capacitors

11.68 Calculate the capacitance of a parallel plate capacitor of area A and thick-

ness d if a dielectric slab of thickness t,areaA and dielectric constant k is

inserted. How is the capacitance modiﬁed if a metal of thickness t is intro-

duced?

11.69 Two capacitors C

and C

are connected in parallel and their combined

capacitance is measured as 9 μF. When they are combined in series their

capacitance is 2 μF. What are t he individual capacitances?

11.70 Find the energy which may be stored in capacitors of 2 and 4 μF when taken

(a) singly, (b) in series and (c) in parallel when a potential difference of 100 V

is available.

[University of New Castle]

11.71 An air capacitor with plates 1 m

and 0.01 m apart is charged with 10

−6

Cof

electricity. Calculate the change in energy which results when the capacitor

is submerged in oil of relative permittivity 2.0.

[University of Manchester]

11.2 Problems 477

11.72 Two parallel plates, each of area 1 m

, are separated by a distance 0.001 m

and have a capacity of 0.1 μF. What must then the dielectric constant of the

material separating the plates be?

[University of Newcastle]

11.73 A capacitor of capacitance 5 μF is charged up to a PD of 250 V. Its terminals

are then connected to those of an uncharged capacitor of capacitance 20 μF.

What would be the resulting voltage?

[Northern Universities of UK]

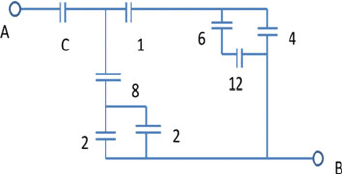
11.74 From Fig. 11.12 ﬁnd the value of capacitance C if the equivalent capacitance

between points A and B is 1 μF. All the capacitances are in microfarads.

[Indian Institute of Technology 1977]

Fig. 11.12

11.75 Three capacitors of capacitance 4, 3 and 2 μF, respectively, are connected in

series to a battery of 240 V. Calculate (a) the charge, (b) the potential and (c)

the electrostatic energy associated with each of the three capacitors, stating

in each case the units in which the results are expressed.

[Northern Universities of U.K.]

11.76 Each of the two capacitors A and B of capacitances 1.0 and 2.0 μF, respec-

tively, are charged initially by connecting them in turn to a 12 V battery. What

is the ﬁnal potential difference of the combination if the capacitors are later

connected in parallel such that

(a) the positive plate of one is connected to the positive plate of the other;

(b) the positive plate of one is connected to the negative plate of the other.

[Indian Institute of Technology 1971]

11.77 Two capacitors of capacitances C

and C

charged to potential difference V

and V

are connected in parallel. Calculate the energy loss when (a) the pos-

itive ends are joined and (b) the positive end of one is joined to the negative

end of the other.

11.78 A capacitor of capacitance C is charged to potential V by connecting it to a

battery. Let q be the charge on it, E the electric ﬁeld within the plates and

U the energy stored. When a dielectric of constant K is introduced ﬁlling

completely the space between the plates, how will the following quantities

478 11 Electrostatics

change (i) V , (ii) E, (iii) q,(iv)C and (v) U, when (a) the battery remains

connected and (b) the battery is disconnected?

11.79 In prob. (11.78) if the plate separation is increased, how would the following

quantities change (i) V , (ii) E, (iii) C,(iv)q and (v) U when (a) the battery

remains connected and (b) the battery is disconnected?

11.80 Show that the force of attraction between the plates of a parallel plate capac-

itorisgivenbyF =

, where A is the area, d the distance of sepa-

ration, V the voltage to which the plates are charged and ε

the permittivity.

11.81 Let n identical droplets, each of radius r and charge q, coalesce to form a

large drop of radius R and charge Q. Assuming that the droplets are incom-

pressible, show that (a) the radius R = n

1/3

r; (b) the capacitance C



of the

large drop is C



= n

1/3

C, where C is the capacitance of the droplet; (c)

the potential V



of the large drop is given by V



= n

2/3

V , where V is the

potential of the droplet; (d) the surface charge density σ



= n

1/3

σ ;(e)the

energy U



stored in the large drop is given by U



= n

5/3

U where U is the

energy stored in the droplet.

11.82 A cylindrical capacitor has radii a and b. Show that half of the stored electri-

cal potential energy lies within a cylinder whose radius is

√

ab.

11.83 A capacitor of capacitance C

= 3.0 μF withstands the maximum voltage

= 4.0 kV, while a capacitor of capacitance C

= 6.0 μF the maximum

voltage V

= 3.0 kV. If they are connected in series what maximum voltage

can the system withstand?

11.84 A Geiger–Muller tube consists of a thin uniform wire of radius ‘a’ of length

L surrounded by a concentric hollow metal cylinder of radius b withagas

of dielectric constant K between them. Apply Gauss’ law to calculate the

capacitance of the tube.

11.85 Two spherical metallic shells of radii a and b (b > a) constitute a capacitor

with the outer shell grounded and contact is made with the inner one through

a hole in the outer one. Show that the capacitance is given by C =

4πε

b − a

11.86 Show that for two concentric shells of radii a and b (b ≈ a), the capacitance

reduces to that of a parallel plate capacitor

11.87 In an R–C circuit the emf supplied by the battery is 120 V, R = 1 × 10



and C = 10 μF. The switch S is closed at t = 0. Find

(i) the time taken for the charge to reach 90% of its ﬁnal value;

(ii) the energy stored in the capacitor at one time constant;

(iii) the Joule heating in the resistor at one time constant.

11.88 After how many time constants will the energy stored in the capacitor in

Fig. 11.13 reach one-half of its equilibrium value?