Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book

Подождите немного. Документ загружается.

11.2 Problems 479

Fig. 11.13

11.89 Two square metal plates measuring ‘a’ on the side are used as a parallel

plate capacitor with the plates slightly inclined at an angle θ . If the smaller

gap between the plates is D, then show that the capacitance is given by

C =



1 −

aθ



11.90 Capacitors C

= 8 μF, C

= 4 μF and C

= 3 μF are arranged as in

Fig. 11.14. A voltage of V = 100 V is applied. Determine

(a) the potential difference across C

, C

and C

(b) the charge q

, q

and q

on C

, C

and C

, U

and U

stored in the capacitors.

Fig. 11.14

11.91 Capacitors C

= 8 μF, C

= 4 μF and C

= 3 μF are arranged as in

Fig. 11.15. A voltage of V = 100 V is applied. Determine

(a) the charges q

, q

and q

on C

, C

and C

, respectively.

(b) the potential difference across C

, C

and C

, U

and U

stored in the capacitors.

Fig. 11.15

11.92 Find the effective capacitance between points a and b in Fig. 11.16. Assume

that C

= C

= 2 μF and C

= 1 μF.

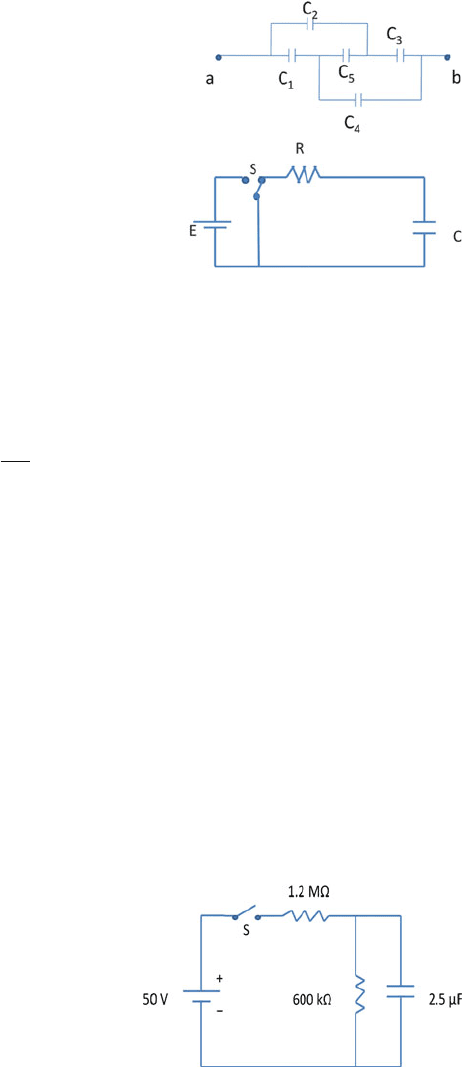
480 11 Electrostatics

Fig. 11.16

Fig. 11.17

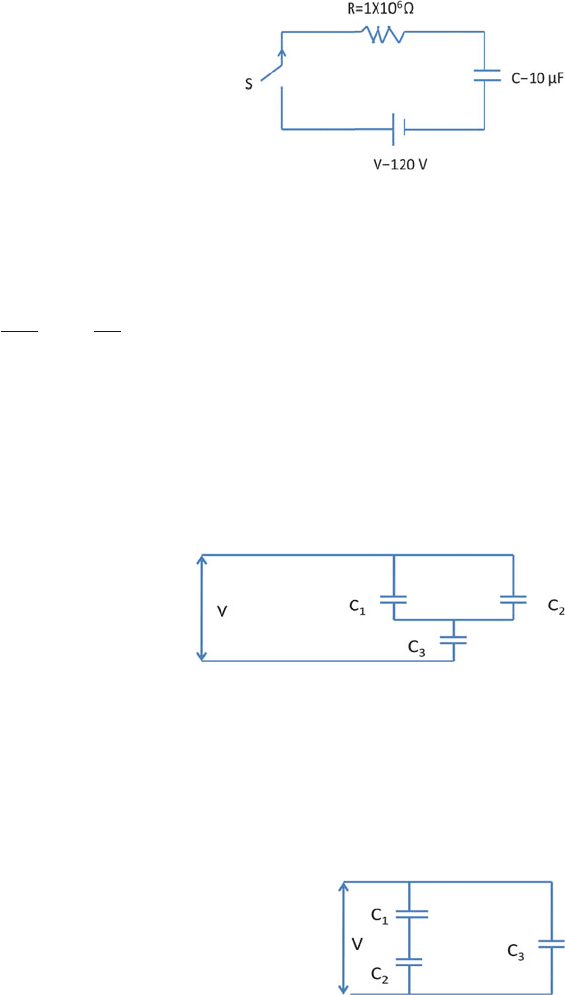
11.93 Consider a circuit consisting of a resistor R and a capacitor C in series

with a battery of emf ξ and a switch (Fig. 11.17). The capacitor is initially

uncharged and the switch is closed at time t = 0. By considering the potential

drop across each of the components of the circuit, verify that the charge Q

on the capacitor has the form

Q = Cξ

⎛

⎝

1 − e

−

⎞

⎠

(a) What is the current ﬂowing in the circuit?

(b) What is the power supplied by the battery as a function of t?

(d) What is the rate at which energy is stored in the capacitor as a function

of t?

[University of Durham 2000]

11.94 For the circuit shown in Fig. 11.18,

(i) What is the initial battery current immediately after switch S is closed?

(ii) What is the battery current a long time after switch S is closed?

(iii) If the switch has been closed for a long time and is then opened, ﬁnd

the current through the 600 k resistor as a function of time.

Fig. 11.18

11.2 Problems 481

11.95 A capacitor of capacitance C = 500 μF is charged to a voltage of 900 V and

is then discharged through a resistance R = 200 k when a switch is closed.

(i) Find the initial charge stored in the capacitor.

(ii) Find the initial discharge current when the switch is closed.

(iii) Find the voltage across the capacitor in a time t = 25 s after the start of

discharge.

(iv) Find the time constant of this capacitor resistor network combination.

(v) Work out an equation to show the time it takes for the charge in the

capacitor to drop by one-half of its starting value and ﬁnd this time.

[University of Aberystwyth, Wales 2008]

11.96 Charge q = 10

−9

C is uniformly distributed in a sphere of radius R = 1m.

(i) Find the divergence of the electric ﬁeld inside the sphere.

(ii) A proton is moved from inﬁnity to r = 0.8 m from the centre of the

sphere. Find the electric force experienced by the proton at r = 0.8m.

(iii) Find the work done by the electric ﬁeld of the charged sphere when the

proton is moved from inﬁnity to its current position (r = 0.8m).

11.97

(a) Write down the integral and differential forms of Gauss’ law in a dielec-

tric, deﬁning all quantities used.

(b) A parallel plate capacitor is completely ﬁlled with a non-conducting

dielectric. Show that the electric displacement, D, is uniform between

the plates and calculate its value. (You may assume that the plates each

have area A and are separated by a small distance d. Each plate carries

a surface charge density σ C/m

K (x) = ax + b

where a and b are constants and x is the perpendicular distance from one

plate. Using Gauss’ law, show that the electric ﬁeld between the plates

satisﬁes

E(x) =

K (x)

where E

is a constant. Find the value of E

(d) Show that the voltage across the capacitor is given by

V =



1 +



and calculate the capacitance.

(e) Find the volume polarization charge density in the dielectric.

482 11 Electrostatics

11.98 Both gravitational ﬁeld and electric ﬁeld obey inverse square law. Using this

analogy show that the differential Gauss’ law for gravitation is given by ∇·

g =−ρ/G, where ρ is the mass density.

11.3 Solutions

11.3.1 Electric Field and Potential

11.1

(a)

(i)

F =

4πε

(8 × 1.6 × 10

−19

)(−4 × 1.6 × 10

−19

)

4π ×8.85 × 10

−12

× (0.2)

=−1.8432 × 10

−25

(ii) For the position of zero electric ﬁeld the forces due to the two charges

must be equal in magnitude but oppositely directed. Clearly the neu-

tral point must be on the x-axis. On the left of Q

, the forces will

be oppositely directed but cannot be equal as |Q

| > |Q

|. Between

and Q

, the forces are exerted in the same direction. On the right

of Q

conditions are favourable for a null point. Let the zero electric

ﬁeld be situated at a distance x from Q

on the right.

(x + 0.2)

−

= 0

whence x = 0.4828 on the r ight of Q

(b) E =

4 πε

1.6 × 10

−19

4π ×8.85 × 10

−12

× (5.3 × 10

−11

)

= 5.12 ×10

N/C

Force F = Ee = 5.12 × 10

× 1.6 × 10

−19

= 81.92 N

11.2

(a) As the electric ﬁeld is downwards, the force on the positive charge will

be downwards and the force on the negative charge will be upwards.

(i)

q =+8 μC

= qE =+8 ×10

−6

× 300 = 2.4 × 10

−3

= mg = 0.6 × 10

−3

× 9.8 = 5.88 × 10

−3

∴ Tension in the thread

T = F

+ F

= 5.88 ×10

−3

+ 2.4 × 10

−3

= 8.28 ×10

−3

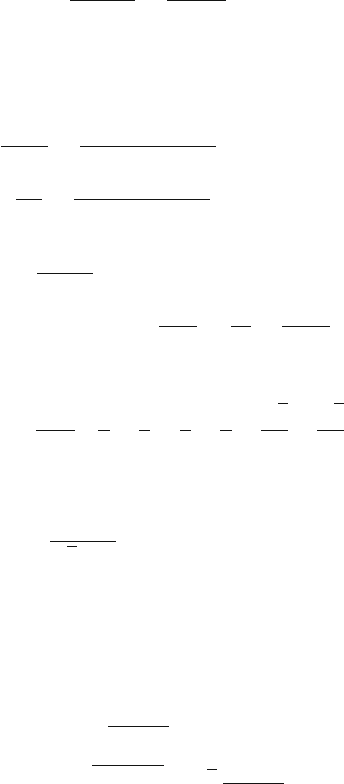
11.3 Solutions 483

(ii)

q =−8 μC

= qE =−2.4 ×10

−3

Tension in the thread

T = 5.88 ×10

−3

− 2.4 × 10

−3

= 3.48 ×10

−3

(b) As the electric ﬁeld is in t he negative x-direction, point b will be at a

higher potential than a.

(i) Therefore V

− V

will be positive

(ii)

E =

− V

(6 − 2)

= 2.5 ×10

N/C

11.3 The total charge on the circular loop Q = 2π Rλ; the distance of the point

P(0, 0, Z) from the loop is r = (Z

)

1/2

. Therefore, the electric potential

P will be

V =

4πε

λR

2ε

+ R

)

1/2

E =−

∂V

∂z

λRZ

2ε

+ R

)

3/2

11.4

(a)

F =

4πε

(Q = 1)

V =−



F dr =−

4πε



4πε

+ C

When r =∞, V = 0. Therefore C = 0

(b) U =

4πε

−

√

−

√

For six pairs of charges

U =−

√

2πε

The potential energy does not depend on the order in which the charges

are assembled.

charges.

= E

=−

8 πε

∴ E =



+ E

√

8 πε

= 0

484 11 Electrostatics

Therefore the charge is not in equilibrium. Same thing is true for the other

three charges.

11.5

(i) V

4πε

2 × 10

−15

× 9 × 10

−3

= 0.018 V

(ii) If n droplets each of radius r coalesce to form a large drop of radius R,

then assuming that the droplets are incompressible, the volume does not

change. Therefore

π R

= n

πr

or R = n

1/3

r (1)

As charge is conserved

Q = nq (2)

where Q and q are the charges on the drop and droplet, respectively. Then

the potential of the droplet is

4πε

1/3

2/3

4πε

= n

2/3

= 2

2/3

= 0.0286 V

where n = 2, and V

= 0.018 V by (i).

11.6 Electric force

F = qE = 2 × 10

−8

× 20, 000 = 4 × 10

−4

Gravitational force mg = 80 × 10

−6

× 9.8 = 7.84 × 10

−4

Balancing the horizontal and vertical components of forces, Fig. 11.19

T sin θ = F (1)

T cos θ = mg (2)

where T is the tension in the thread.

Fig. 11.19

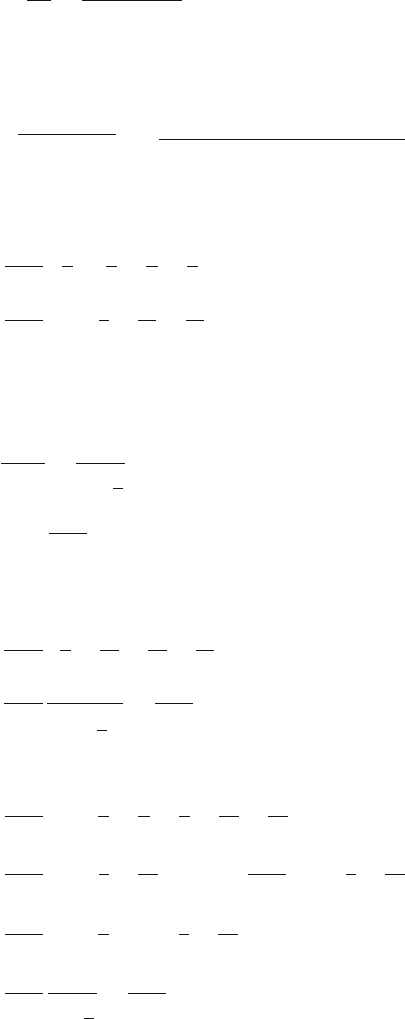
11.3 Solutions 485

tan θ =

4 × 10

−4

7.84 × 10

−4

= 0.51

θ = 27

◦

Squaring (1) and (2) and adding and extracting the square root

T =



+ (mg)



(4 × 10

−4

)

+ (7.84 × 10

−4

)

= 8.8 ×10

−4

11.7 Electric potential

V =

4πε



+···



4πε



1 +

+···



The terms in brackets form a geometric progression of inﬁnite terms whose

sum is

S =

1 −r

1 −

= 2

∴ V =

2πε

Electric ﬁeld

E =

4πε



+···



4πε



1 −



3πε

11.8

V =

4πε



q −

−

+···



4πε



1 +

+···



−

8πε



1 +

+···



4πε



q −





1 +

+···



8πε

1 −

6πε

486 11 Electrostatics

E =

4πε



q −

−

···



4πε



1 +

+···



−

16πε



1 +

+···



4πε



q −





1 +

+···



16πε

1 −

5πε

11.9 By prob. (11.3), E =

4πε



+ R



3/2

, where we have replaced z by x and

substituted λ = Q/2π R.Asx << R and F = qE,

F =

Qq x

4πε

=−kx, where q is negative and k =

4πε

−5

× 10

−6

× 9 × 10

= 0.09

Thus, the motion of the negatively charged particle is approximately simple

harmonic with angular frequency

ω =



0.09

0.9 × 10

−3

= 10

T =

2π

= 0.628 s

11.10 Let a be the side of the equilateral triangle. The forces on the charge q placed

at C due to the charges at A and B are repulsive and represented by CE and

CD, respectively, each given by q

/4πε

. The resultant of these two forces

is given by CP, the diagonal of the parallelogram CDPE, Fig. 11.20

CP = 2CD cos 30

◦

4πε

√

4πε

The force on q at C due to Q at the centre of the triangle is

4πε

(OC)

3Qq

4πε

i. If Q =−q, this force will be attractive and will be directed along CO. As

the attractive force due to −q is greater than the combined repulsive force

due to charges +q at A and B, the charge at C will be attracted towards

O. Same is true for the charges placed at A and B.

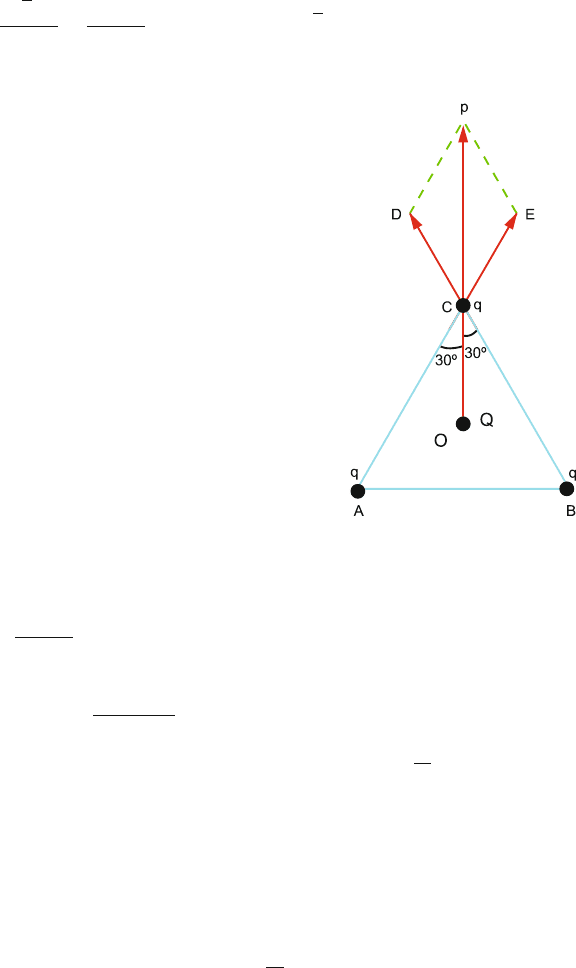
11.3 Solutions 487

ii. For equilibrium, the attractive force must balance the repulsive force:

√

4πε

−

3Qq

4πε

= 0 → Q =−q/

√

Fig. 11.20

11.11 Referring to Fig. 11.21, the Coulomb force between the spheres in air is

F =

4πε

In liquid F



4πε

; weight of the sphere in air = mg

Apparent weight of the sphere in liquid = mg



1 −





, where ρ is the

density of the material of sphere and ρ



that of the liquid. For equilibrium

the vertical and horizontal components of the force must separately balance.

If T is the tension in the string when the sphere is in air and T



when it is in

the liquid,

T sin θ = F, T cos θ = mg



sin θ = F



, T



cos θ = mg



1 −





488 11 Electrostatics

tan θ =



1 −







= K =

1 −



ρ −ρ



1.6

1.6 − 0.8

= 2

Fig. 11.21

11.12 From the geometry of Fig. 11.22,AB= 0.1m, OB = OC = 0.05

√

2m,

AC = (0.1)

√

2m.

Potential energy of q at B is U(B) =

4πε





Potential energy of q at C is U(C) =

4πε





Fig. 11.22