Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.

448 10 Heat and Matter
During the isochoric heating and cooling no work can be done by or on
the gas:
Q = U =
2
1
dU = C
v
T
2
T
1
dT = C
v
(T
2
− T
1
) (1)
so that
Q
out
= C
v
(T
B
− T
C
), Q
in
= C
v
(T
A
− T
D
) (2)
where the heats (positive) are those which are given out and put into the
system, respectively. The thermodynamic efficiency
e =
work done by the gas
heat put into the system
=
W
Q
in
(3)
Since the internal energy does not change over the entire cycle, by first
law of thermodynamics, net heat added to the system equals the work
done by the system, so that
W = Q
in
− Q
out
(4)
e =
W
Q
in
=
Q
in
− Q
out
Q
in
= 1 −
Q
out
Q
in
=
1 −
T
B
− T
C
T
A
− T
D
(5)
In an adiabatic expansion or compression
TV
γ −1
= constant (6)
∴ T
A
V
γ −1
A
= T
B
V
γ −1
B
, T
D
V
γ −1
D
= T
C
V
γ −1
C
(7)
or T
A
= T
B
V
B
V
A
γ −1
, T
D
= T
C
V
C
V
D
γ −1
(8)
From Fig. 10.11 we note that
V
B
V
A
=
V
C
V
D
= r (compression ratio) (9)
Using (8) and (9) in (5)
e = (1 −r
1−γ
) (10)
Thus the higher the compression ratio the greater is the efficiency.
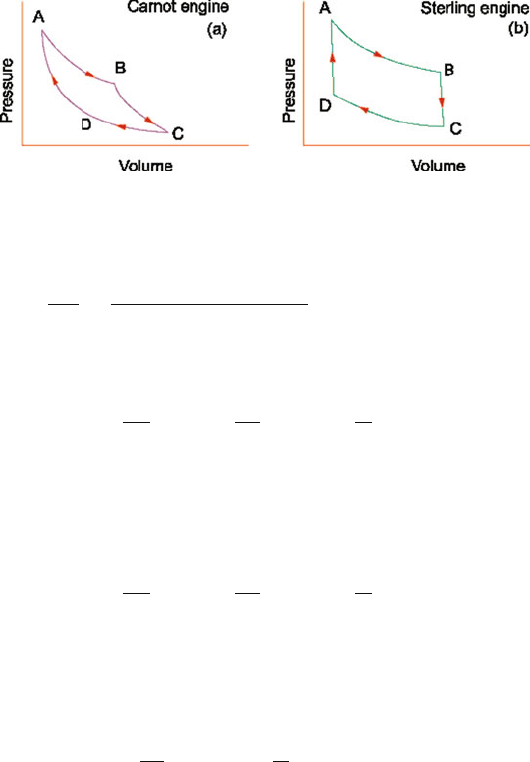
10.3 Solutions 449
(c)
Fig. 10.12 (a) Carnot cycle consisting of two isothermic processes AB and CD; two adiabatic
processes BC and DA. (b) Sterling cycle consisting of two isothermic process AB and CD, two
isochoric processes BC and DA
10.51
(a)
n =
PV
RT
=
1.013 × 10
5
× 1 × 10
−3
8.31 × 273
= 0.04465 mol
(i)
dQ = nC
P
dT
S =
T
f
T
i
dQ
T
= nc
p
T
f
T
i
dT
T
= nc
p
ln
T
f
T
i
= 0.04465 ×21 × ln(500/273) = 0.567 J/K
(ii)
dQ = nC
v
dT
S =
T
f
T
i
dQ
T
= nc
v
T
f
T
i
dT
T
= nc
v
ln
T
f
T
i
= 0.04465 ×12.7 × ln(500/273) = 0.343 J/K
(b)
dQ
1
= mC
v
dT
S
1
= mC
v
T
f
T
i
dT
T
= mC
v
ln
T
f
T
i
= 1.0 ×4.13 ×10
3
× ln(313/273) = 695 J/K
When 0.5 kg water at 0
◦
C is mixed with 0.5 kg water at 100
◦
C, the final
temperature would be 50
◦
C.
S
2
= 0.5 ×4.13 ×10
3
× ln(313/273)
+ 0.5 × 4.13 × 10
3
× ln(313/373)
= 282.35 −362.15 =−79.8J/K

450 10 Heat and Matter
10.52
(a) The internal energy of an ideal gas is given by U = nC
V
T . In isothermal
expansion where the temperature and the amount of gas remain constant,
the internal energy does not change. Thus U = 0.
(b) The work done is
W =−
V
2
V
1
PdV =−
V
2
V
1
nRT
V
dV
=−nRT
V
2
V
1
dV
V
=−nRT ln(V
2
/V
1
).
(c) Using the first law of thermodynamics, Q = U + W, and putting
U = 0, we have
Q = W = nRT ln(V
2
/V
1
)
(d) The change in entropy is
S =
ds =
dQ
T
=
1
T
dQ
because the temperature T does not change. Thus
S = nR ln(V
2
/V
1
)
(e) By assumption the temperature of the reservoir does not change and
because it loses heat Q to the gas, the entropy change of the reservoir
will be
S
res
=−S =−nRln(V
2
/V
1
)
Therefore the entropy change of the system plus the reservoir equals
zero, which is the definition of a reversible process.
10.53
(a) The internal energy U of a system tends to increase if energy is added
as heat Q and tends to decrease if energy is lost as work W done by the
system.
Heat is energy that is transferred from one body to another due to differ-
ence in temperature of the bodies.
Enthalpy (H) is the total heat and is defined by
H = U + PV

10.3 Solutions 451
Work (W) is energy that is transferred from one body to another body
due to a force that acts between them.
The function, G = U +PV −TS, is known as Gibb’s function or Gibb’s
energy.
Relations:
(i) Enthalpy
H = U + PV (1)
dH = dU + PdV + V dP = Tds + V dp (2)
∵ T ds = dU + PdV (3)
It follows that enthalpy is a function of entropy (S) and pressure
(P).
∴ H = f (S, P)
dH =
∂ H
∂ S
P
dS +
∂ H
∂ P
S
dP (4)
Comparing (4) with (2)
∂ H
∂ S
P
= T and
∂ H
∂ P
S
= V (5)
(ii) Gibb’s function:
G = U + PV − TS (6)
dG = dU + PdV + V dP − T dS − SdT
But T dS = dU + PdV
∴ dG = VdP − SdT (7)
Thus G is a function of two independent variables P and T .
G = f (P, T )
dG =
∂G
∂ P
T
dP +
∂G
∂T
P
dT (8)
Comparing (8) with (7)
∂G
∂ P
T
= V (9)
∂G
∂ P
P
=−S (10)

452 10 Heat and Matter
(iii) Internal energy:
dQ = T dS (11)
dU = dQ − dW (12)
dW = PdV (isobaric process) (13)
∴ dU = dQ − PdV (14)
dU = T dS − PdV (15)
∴
∂U
∂ S
V
= T (16)
∴
∂U
∂V
S
=−P (17)
(b) The quantities U, T , S, P and V are functions of the condition or state of
the body only, in other words, all the differentials are perfect differentials
and are state variables. Since the differentials which occur in (15) are
perfect differentials, they are valid for all changes whatever their nature.
On the other hand, dQ is not a perfect differential, but represents only
an infinitesimal quantity of heat, and for a cycle
dQ is not zero, but is
equal to the work done. Similarly, dW is also not a perfect differential.
Note that the internal energy, the entropy and the volume are all pro-
portional to the mass of the substance under consideration, while the
temperature and the pressure are independent of it.
The condition of a given mass of a body (say 1 mol) can be defined by
U, T , S, P, V or combinations of them, of which only two are indepen-
dent. It follows that enthalpy and Gibb’s function are also acceptable as
state functions, apart from the internal energy but not the heat or work.
10.3.6 Elasticity
10.54
(a) η =
shear stress
shear strain
=
F/A
x/y
=
100 × 10
6
/1
2
0.1/10
= 10
10
Pa
(b) K =
P
(−V/V )
=
100 × 10
6
1/100
= 10
10
Pa
10.55
(i)
Stress =
force
area
=
mg
A
=
20 × 9.8
20 × 10
−6
= 9.8 ×10
6
Pa
(ii)
Strain =
elongation
original length
=
2.5 × 10
−2
10
= 2.5 ×10
−3
(iii)
Young’s modulus =
stress
strain
=
9.8 × 10
6
2.5 × 10
−3
= 3.92 ×10
9
Pa

10.3 Solutions 453
10.56 For a perfect gas of 1 mol
PV = RT (1)
Under isothermal conditions T = constant. Differentiating (1)
PdV + V dP = 0(2)
The bulk modulus for the isothermal process
K
T
=−V
dP
dV
T
= P (3)
For adiabatic compression in which heat of compression remains in the gas
PV
γ
= constant (4)
where γ = C
p
/C
v
is the r atio of specific heats at constant pressure and
constant volume. Differentiating (4)
γ PV
γ −1
dV + V
γ
dP = 0(5)
Thus adiabatic elasticity K
H
is given by
K
H
=−V
dP
dV
H
= γ P (6)
It follows that
K
H
= γ K
T
(7)
The adiabatic elasticity is greater than the isothermal elasticity by a factor γ
which is always greater than unity.
10.57
Y = 2η(1 + σ)
∴ σ =
Y
2η
− 1 =
1
2
× 2.5 − 1 = 0.25
10.58 From Fig. 10.13 the new length L
= 2AD = 2
AC
2
+ CD
2
= 2
(0.6)
2
+ (0.02)
2
= 1.200666 m
Elongation of the wire, L = L
− L = 1.200666 − 1.20 = 0.000666 m.
Strain = L/L = 0.000666/1.2 = 5.55 × 10
−4
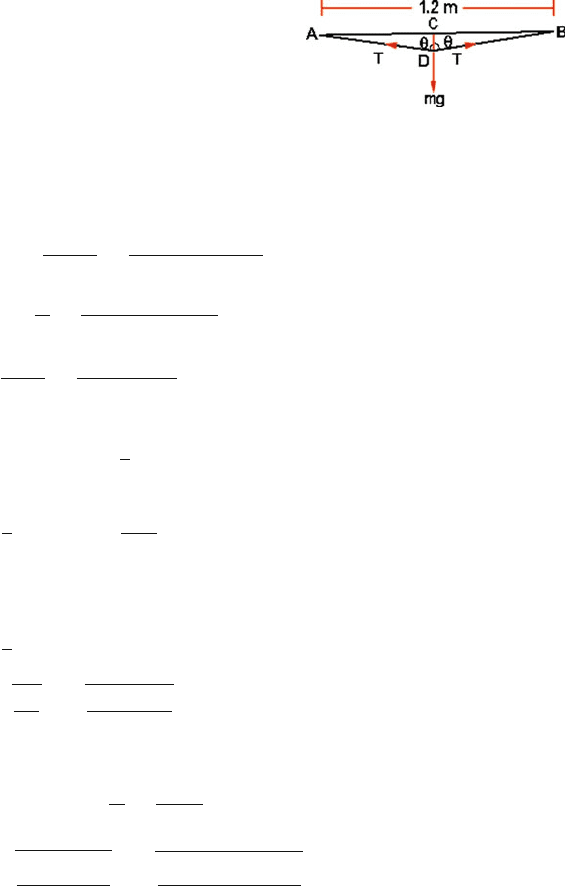
454 10 Heat and Matter
Fig. 10.13 Load fixed to the
midpoint of a horizontal wire
For equilibrium
2T cos θ = mg
F = T =
mg
2 cos θ
=
29 × 10
−3
× 9.8
2 × (0.02/60)
= 426.3N
Stress =
F
A
=
426.3
π(0.05 × 10
−3
)
2
= 5.43 ×10
10
Pa
Y =
stress
strain
=
5.43 × 10
10
5.55 × 10
−4
= 9.78 ×10
13
Pa
10.59 Elastic energy E =
1
2
Y (strain)
2
(volume)
E =
1
2
× 6 × 10
8
0.05
0.20
2
(2 × 10
−6
× 0.25) = 9.375 J
The elastic energy is converted into kinetic energy.
E =
1
2
mv
2
v =
2E
m
=
2 × 9.375
15 × 10
−3
= 35.3m/s
10.60 F = mω
2
r
Breaking stress =
F
A
=
mω
2
r
A
= 4.8 ×10
7
ω =
4.8 × 10
7
A
mr
=
4.8 × 10
7
× 10
−6
10 × 0.3
= 4rad/s
10.61 Stretching force = weight of the wire = (volume) (density) ×g
F = LAρg
where L is the length of wire, ρ the density, A the area of cross-section and
g the acceleration due to gravity.

10.3 Solutions 455
Breaking stress = maximum stretching force/area
=
LAρg
A
= Lρg
7.8 × 10
8
= L × 7800 × 9.8
∴ L = 1.021 ×10
4
m = 10.2km
Note that the result is independent of cross-sectional area of the wire.
10.3.7 Surface Tension
10.62 S =
h +
r
3
rρg
2 cos θ
Assuming that the contact angle θ = 0
h =
2s
r ρg
−
r
3
=
2 × 0.072
10
−3
× 10
3
× 9.8
−
10
−3
3
= 0.01436 m
= 1.436 cm
10.63 Pressure due to water column of depth h is
P = hgρ
Total pressure of the bubble, ignoring surface tension,
P
= P + P
0
= hgρ + P
0
= 100 ×9.8 ×1000 + 1.01 × 10
5
= 10.81 ×10
5
P
V = nRT
∴ V =
nRT
P
=
1 × 8.314 × 293
10.81 × 10
5
= 2.25 ×10
−3
m
3
10.64 As the drops are incompressible, the volume is constant.
n
4
3
πr
3
=
4π
3
R
3
∴ R = rn
1/3
Decrease in surface area = 4πr
2
n − 4π R
2
= 4πr
2
n − n
2/3
Energy released = (decrease in surface area) (surface tension)

456 10 Heat and Matter
W = 4πr
2
n − n
2/3
s
Also W = 4π R
2
S
n
1/3
− 1
Then there will be a rise in temperature as energy is converted into heat.
Energy conservation gives
mcθ = 4π R
2
s
n
1/3
− 1
4π
3
R
3
cρθ = 4πsR
3
1
r
−
1
R
∴ θ =
3s
ρc
1
r
−
1
R
10.65 W = 2 ×4π
r
2
2
−r
2
1
S
The factor of 2 arises as there are two surfaces.
W = 8π
(0.05)
2
− (0.01)
2
× 0.03
= 0.0018 J
10.66 The excess pressure must be equal to the pressure due to the water column
of depth h before the water leaks into the vessel.
2S
r
= ρ gh
∴ r =
2s
ρgh
=
2 × 0.073
1000 × 9.8 × 0.45
= 0.033 ×10
−3
m = 0.033 mm
10.67 Balancing the excess pressure in the bubble with the pressure due to a water
column of depth h
2S
r
= ρgh
∴ h =
2s
rρg
=
2 × 0.072
0.3 × 10
−3
× 1000 × 9.8
= 0.049 m = 4.9cm
10.68 h =
2s
rρg
=
2 × 0.073
0.2 × 10
−3
× 1000 × 9.8
= 0.07449 m = 7.45 cm
The tube is inadequate as it is only 6 cm long. Water will not overflow. But the
radius of meniscus r
1
would now increase such that the following condition
is satisfied:

10.3 Solutions 457
h
1
r
1
= hr, where r
1
is the radius of the meniscus.
r
1
=
hr
h
1
=
7.45 × 0.2
6.0
= 0.248 mm
10.69 When a bubble is charged, the charges stick to the bubble’s surface and due to
mutual repulsion tend to expand the surface while the surface tension tends
to decrease the surface. An equilibrium is reached with a smaller excess of
pressure.
Pressure due to electric charge is
P =
σ
2
2ε
0
where σ is the charge density and ε
0
is the permittivity.
If the excess pressure due to surface tension is neutralized by the electric
charges then
σ
2
2ε
0
=
4S
r
or σ =
8ε
0
S
r
The charge
q = 4πr
2
σ = 8π
2ε
0
sr
3
= 8π
2 × 8.85 × 10
−12
× 0.03 × (0.02)
3
= 2.06 ×10
−9
C
10.70 Under isothermal conditions
P
1
V
1
+ P
2
V
2
= PV (1)
P
1
=
4S
r
1
, P
2
=
4S
r
2
, P =
4S
r
(2)
V
1
=
4π
3
r
3
1
, V
2
=
4π
3
r
3
2
, V =
4π
3
r
3
(3)
Using (2) and (3) in (1) and simplifying we get
r =
r
2
1
+r
2
2
(4)
