Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.

11.3 Solutions 499
Fig. 11.34
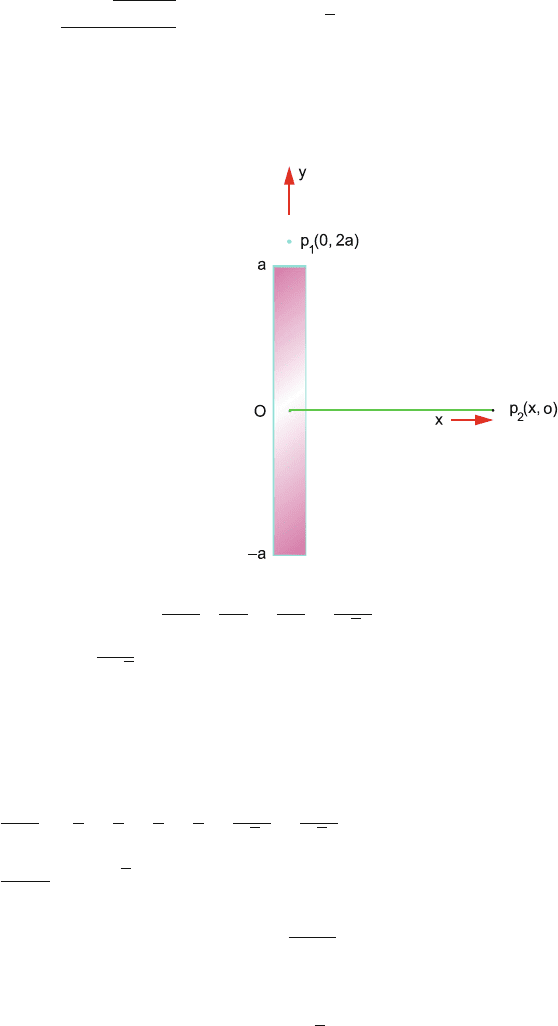
11.35 Let the charge q be taken from the centre of ring A to the centre of ring B,
Fig. 11.35
At A, U
A
=
qQ
1
4πε
0
R
+
qQ
2
4πε
0
(
√
2 R)
At B, U
B
=
qQ
2
4πε
0
R
+
qQ
1
4πε
0
(
√
2 R)
Work done, W = U
B
−U
A
=
(
√
2 − 1) q (Q
2
− Q
1
)
4
√
2πε
0
R
Fig. 11.35
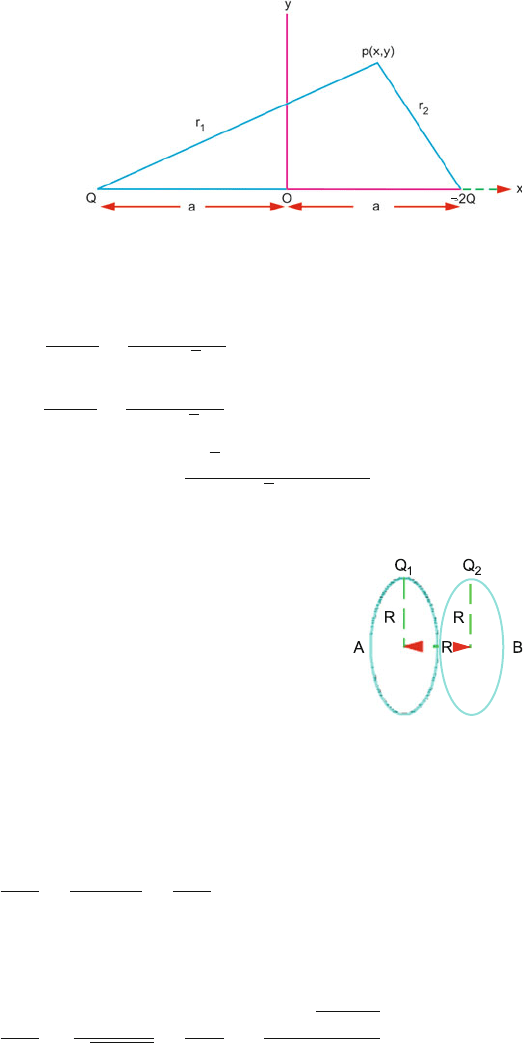
11.36
(a) Consider an infinitesimal length of the rod, at distance y from the origin,
Fig. 11.36. The charge in dy will be λdy. The distance of P
1
from dy
will be 2a − y. The potential at P
1
is
V
1
=
1
4πε
0
a
−a
λ dy
(2a − y)
=
λ
4πε
0
ln 3
The potential at P
2
is
V
2
=
1
4πε
0
a
−a
λdy
y
2
+ x
2
=
2λ
4πε
0
ln
a +
√
a
2
+ x
2
x
500 11 Electrostatics
By problem V
2
= V
1
∴
a +
√
a
2
+ x
2
x
2
= 3 → x =
√
3a
V
1
= V
2
= λ × 9 × 10
9
× ln 3
= 9.89 × 10
9
V
Fig. 11.36
11.37 U = U
Qq
+U
Qq
+U =
1
4πε
0
Qq
a
+
Qq
a
+
q
2
√
2a
= 0 by problem.
Therefore Q =−
q
2
√
2
·
11.38 Work done W = U
12
+U
23
+U
34
+U
41
+U
13
+U
24
where charges l and
3 are positive and 2 and 4 negative assuming that the potential energy is zero
for infinite separation of charges.
W =
q
2
4πε
0
−
1
a
−
1
a
−
1
a
−
1
a
+
1
√
2a
+
1
√
2a
=
−q
2
4πε
0
a
4 −
√
2
11.39
(a) The charge density is given by ρ =
3q
4π R
3
. Consider a shell of radius
r and thickness dr concentric with the sphere. The volume of the shell
is 4πr
2
dr and the charge in it will be dq = 4πr
2
drρ,Fig.11.37.The
charge of the sphere of radius r is dq
=
4
3
πr
3
ρ and may be considered
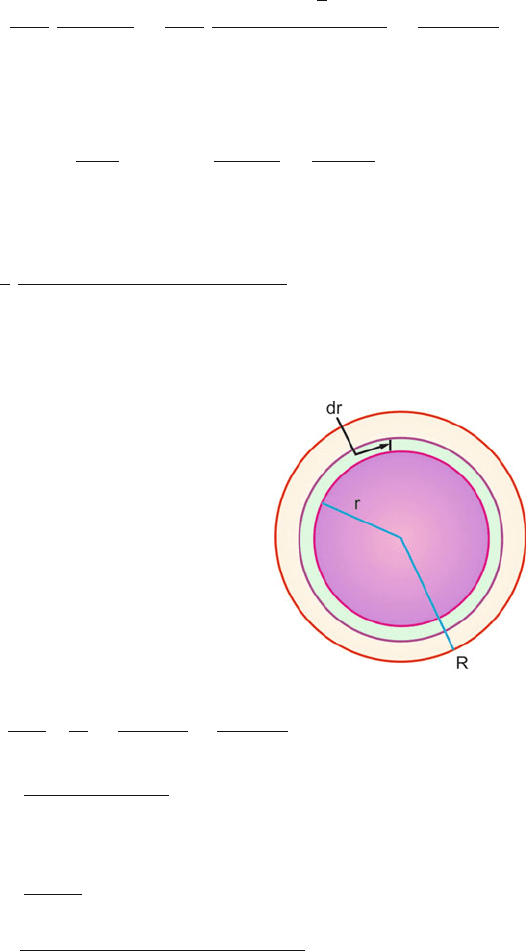
11.3 Solutions 501
to be concentrated at the centre. The interaction energy between the shell
and the sphere of radius r will be
dU =
1
4πε
0
(dq)(dq
)
r
=
1
4πε
0
(4πr
2
drρ)
4
3
πr
3
ρ
r
=
4πρ
2
r
4
dr
3ε
0
Total interaction energy
U =
dU =
4πρ
2
3ε
0
R
0
r
4
dr =
4πρ
2
R
5
15ε
0
=
3q
2
20πε
0
R
where we have substituted the value of ρ.
(b)
U =
3
5
×9 × 10
9
× (92 × 1.6 × 10
−19
)
2
1.5 × (238)
1/3
× 10
−15
= 1.259 ×10
−11
J
= 78.7MeV
Fig. 11.37
11.40
(i)
E =
Q
4πε
0
2
x
2
−
1
(x + d)
2
−
1
(x − d)
2
=−
2Qd
2
(3x
2
− d
2
)
4πε
0
x
2
(x
2
− d
2
)
2
(ii)
For x >> d, 3x
2
− d
2
3x
2
and x
2
− d
2
x
2
E =−
6Qd
2
4πε
0
x
4
(iii)
E =−
6 × 9 × 10
9
× 2 × 10
−6
× (10
−4
)
2
(0.2)
2
= 0.675 N/C
502 11 Electrostatics
11.41
(a)
q = CV = 4πε
0
rV=
5 × 10
6
× 10
−3
9 × 10
9
= 5.5 ×10
−7
C
(b)
V =
q
4πεr
=
5.5 × 10
−7
× 9 × 10
9
1 × 10
−3
= 1.65 ×10
6
V
11.42
Initial potential energy U
1
=−
qe
4πε
0
r
1
Final potential energy U
2
=−
qe
4πε
0
r
2
U = U
1
−U
2
=
qe
4πε
0
1
r
2
−
1
r
1
By work–energy theorem, gain in kinetic energy = loss in potential energy.
1
2
mv
2
=
qe
4πε
0
1
r
2
−
1
r
1
v =
2qe
4πε
0
m
1
r
2
−
1
r
1
1/2
=
2 × 2 × 10
−9
× 1.6 × 10
−19
× 9 × 10
9
9.1 × 10
−31
1
0.18
−
1
1.2
1/2
= 5.467 ×10
6
m/s
11.43
V (r) =
Q
4πε
0
2
r
−
1
√
r
2
+ d
2
−
1
√
r
2
+ d
2
=
2Q
4πε
0
1
r
−
1
r
1 +
d
2
r
2
−1/2
!
Qd
2
4πε
0
r
3
Thus V (r)α
1
r
3
11.44
(i) F = qE = (1.6 × 10
−19
)(2 × 10
3
) = 3.2 × 10
−16
N
(ii)
Acceleration a =
F
m
=
3.2 × 10
−16
9.1 × 10
−31
= 3.516 ×10
14
m/s
2
v =
√
2as =
2 × 3.516 × 10
14
× 0.015
= 3.25 ×10
6
m/s
(iii) Outside the plates there is no force on the electron as there is no electric
field.
11.45
V (r) =
Q
4πε
0
r
(1)
For continuous distribution of charge, each element dq can be treated as point
charge so that the contribution dV to the potential can be written according
to (1), Fig. 11.38:

11.3 Solutions 503
Fig. 11.38
dV =
1
4πε
0
dQ
r
(2)
For the potential due to the entire distribution of all the elements, (2) is
integrated:
V =
dV =
1
4πε
0
dQ
r
(3)
In case of uniform charge distribution we can write dQ = λ ds,dQ = σ dA
or dQ = ρdV depending on the geometry of the problem. Here λ is the
linear charge density, σ is the surface charge density and ρ is the volume
charge density.
(a) q = π R
2
σ
(b) Consider a ring of radius r and width dr concentric with the disc of
radius R. The charge on the ring is dq = σ2πrdr. The potential at P, at
a distance x on the axis of the disc, will be
dV =
1
4πε
0
dq
y
=
1
4πε
0
σ 2πr dr
√
r
2
+ x
2
(4)
Potential due to the disc will be
V =
dV =
σ
2ε
0
R
0
r dr
√
r
2
+ x
2
(5)
Put r
2
+ x
2
= y
2
, r dr = y dy, then (5) becomes
V =
σ
2ε
0
dy =
σ
2ε
0
y
√
x
2
+R
2
|
x
=
σ
2ε
0
x
2
+ R
2
− x
(6)
504 11 Electrostatics
(c) If x >> R, (6) can be expanded binomially,
V →
σ
2ε
0
x
1 +
R
2
x
2
1/2
− x
!
=
σ R
2
4ε
0
x
=
q
4πε
0
x
, an expression
which is appropriate for the point charge. This result is reasonable since
at very large distances the disc appears as a point.
11.46 For circular motion of electron, the speed
v =
2πr
T
(1)
For a stable orbit, the centripetal force = electric force.
mv
2
r
=
1
4πε
0
e
2
r
2
(2)
Eliminating v between (1) and (2)
T
2
= 16π
3
ε
0
mr
3
or T
2
α r
3
(Kepler’s third law)
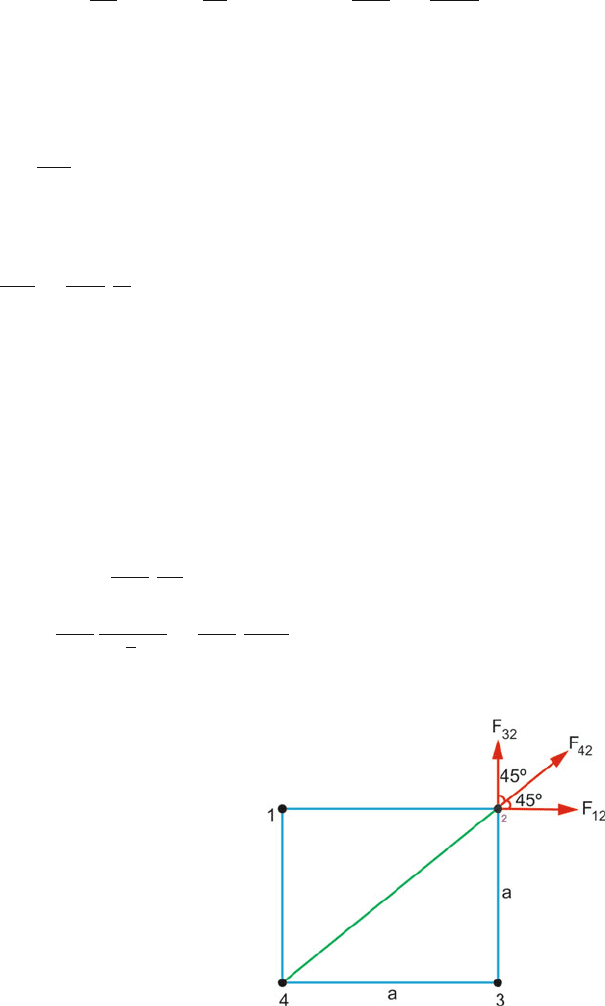
11.47 Figure 11.39 shows the forces on charge 2 due to the charges 1, 3 and 4. The
forces
F
12
= F
32
=
1
4πε
0
Q
2
a
2
F
42
=
1
4πε
0
Q
2
√
2a
2
=
1
4πε
0
Q
2
(2a
2
)
Fig. 11.39

11.3 Solutions 505
Now
|
F
32
+ F
12
|
=
√
2 F
12
(∵ F
12
and F
32
act at right angle and are equal
in magnitude)
Further, F
42
acts in the same direction as the combined force of F
32
and
F
12
.
∴
|
F
12
+ F
32
+ F
42
|
=
Q
2
4πε
0
a
2
√
2 +
1
2
=
1.914 Q
2
4πε
0
a
2
11.48 (a) A dipole consists of two equal and opposite charges. To find the electric
field at A, on the perpendicular bisector of the dipole, at distance x.As
the point A is equidistant from the two charges, the magnitudes E
+
and
E
−
are equal. The net electric field E at A is given by the vector addition
of E
+
and E
−
(Fig. 11.40)
E = E
+
+ E
−
(1)
E
+
= E
−
=
1
4πε
0
q
r
2
=
1
4πε
0
q
[x
2
+ (d/2)
2
]
(2)
Since both E
+
and E
−
are equal and equally inclined to the y-axis, their
x-components gets cancelled and the combined field is contributed by
the y-component alone.
Fig. 11.40
E = E
y
= E
+
cos θ + E
−
cos θ = 2E
+
cos θ
=
1
4πε
0
qd
[x
2
+ (d/2)
2
]
3/2
(3)
(b) For x >> d/2, E =
1
4πε
0
p
x
3
, where p = qd is the dipole. Thus
the electric field at large distance varies inversely as the third power of
distance, which is much more rapid than the inverse square dependence
for point charge.
(c) Potential energy U =−P · E =−pE cos θ , for parallel alignment,
θ = 0, and
U
1
=−pE =−(6 × 10
−32
)(3 × 10
6
) =−1.8 × 10
−25
J
506 11 Electrostatics
For antiparallel arrangement, θ = 180
◦
and U
2
=+PE =+1.8 ×
10
−25
J.
Therefore the difference in the potential energy U = U
2
−U
1
= 3.6 ×
10
−25
J.
11.3.2 Gauss’ Law
11.49
(a) If φ
E
is the electric flux, E the electric field, q the charge enclosed and
dA the element of area then q = ε
0
5
E · dA. The integration is to be
carried over the entire surface. The circle on the integral sign indicates
that the surface of integration is a closed surface.
(b) Figure 11.41 shows a portion of a thin non-conducting infinite sheet of
charge of constant charge density σ (charge per unit area). To calculate
the electric field at points close to the sheet construct a Gaussian surface
in the form of a closed cylinder of cross-sectional area A, piercing the
plane of the sheet, Fig. 11.41. From symmetry, it is obvious that E points
are at right angle to t he end caps, away from the plane, and are positive
at both the end caps. There is no contribution to the flux from the curved
wall of the cylinder as E does not pierce. By Gauss law
ε
0
E · dA = q
ε
0
(EA+ EA) = q
where σ A is the enclosed charge. Thus E = σ/2ε
0
·
Fig. 11.41

11.3 Solutions 507
For a non-conducting sheet the field
E =
σ
2ε
0
(1)
The electric force acting on the sphere is
F = qE =
qσ
2ε
0
(2)
(c) The sphere is held in equilibrium under the joint action of three forces:
(1) Weight acting vertically down,
(2) Electric force F acting horizontally, and
(3) Tension in the thread acting along the thread at an angle θ with the
vertical.
From Fig. 11.42, F/mg = tan θ (3)
Combining (2) and (3)
σ =
2ε
0
mg tan θ
q
=
2 × 8.9 × 10
−12
× 2 × 10
−6
× 9.8 × tan 10
◦
5 × 10
−8
= 2.15 ×10
−11
C/m
2
Fig. 11.42

508 11 Electrostatics
11.50
(a) Integral form of Gauss’ law:
E · ds =
Q
ε
0
Differential form: ∇·E =
ρ
ε
0
(b) r > R. Construct a Gaussian surface in the form of a sphere of radius
r > R, concentric with the charged sphere of radius R,Fig.11.43a.
By Gauss’ law
E · dA = (E) 4π r
2
=
Q
ε
0
∴ E =
Q
4πε
0
r
2
(1)
Fig. 11.43
(a) (b)
(c) r < R. Construct a Gaussian surface in the form of a sphere of radius
r < R, concentric with the charged sphere of radius R,Fig.11.43b. Let
charge q
reside inside the Gaussian surface. Then by Gauss’ law
ε
0
E · dA = (ε
0
E)(4πr
2
) = q
E =
q
4πε
0
r
2
(2)
Now the charge outside the sphere of radius r does not contribute to the
electric field. Assuming that ρ is constant throughout the charge distri-
bution,
q
q
=
4
3
πr
3
4
3
π R
3
or q
= q
r
3
R
3
(3)
Using (3) in (2), E =
1
4πε
0
qr
R
3
(4)
