Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.


328 7 Lagrangian and Hamiltonian Mechanics
which yield the equations of motion
(M + m) ¨x −mr
¨
θ = 0 (15)
¨x −r
¨
θ − g θ = 0 (16)
Equations (15) and (16) constitute the equations of motion. Eliminating ¨x
we obtain
¨
θ +
M + m
M
g
r
θ = 0 (17)
which is the equation for simple harmonic motion with frequency ω =
(M + m)
M
g
r
and time period
T =
2π
ω
= 2π
M
(M + m)
r
g
(18)
On comparing (18) with (8) it is observed that the period of oscillation is
smaller by a factor [M/(M + m)
1/2
] as compared to the case where the
bowl is fixed.
7.28 Take the differential of the Lagrangian
L(q
1
,...,q
n
, ˙q
1
,..., ˙q
n
, t)
dL =
n
r=1
∂ L
∂q
r
dq
r
+
∂ L
∂ ˙q
r
d ˙q
r
+
∂ L
∂t
dt (1)
Now the Lagrangian equations are
d
dt
∂ L
∂ ˙q
r
−
∂ L
∂q
r
= 0(2)
and the generalized momenta are defined by
∂ L
∂ ˙q
r
= p
r
(3)
Using (3) in (2) we have
d
dt
∂ L
∂ ˙q
r
=˙p
r
(4)

7.3 Solutions 329
Using (2), (3) and (4) in (1)
dL −
n
r=1
( ˙p
r
dq
r
+ p
r
d ˙q
r
) +
∂ L
∂t
dt (5)
Equation (5) can be rearranged in the form
d
n
r=1
p
r
˙q
r
− L
=
n
r=1
( ˙q
r
dp
r
−˙p
r
dq
r
) −
∂ L
∂t
dt (6)
The Hamiltonian function H is defined by
H =
n
r=1
p
r
˙q
r
− L(q
1
,...,q
n
, ˙q
1
,..., ˙q
n
, t) (7)
Equation (6) therefore my be written as
dH =
n
r=1
( ˙q
r
dp
r
−˙p
r
dq
r
) −
∂ L
∂t
dt (8)
While the Lagrangian function L is an explicit function of q
1
,...,q
n
,
˙q
1
,..., ˙q
n
and t, it is usually possible to express H as an explicit function only
of q
1
,...,q
n
, p
1
,..., p
n
, t, that is, to eliminate the n generalized velocities
from (7). The n equation of type (3) are employed for this purpose. Each
provides one of the p’s in terms of the ˙q
s. Assuming that the elimination of
the generalized velocities is possible, we may write
H = H(q
1
,...,q
n
, p
1
,..., p
n
, t) (9)
H now depends explicitly on the generalized coordinates and generalized
momenta together with the time. Therefore, taking the differential dH,we
obtain
dH =
n
r=1
∂ H
∂q
r
dq
r
+
∂ H
∂p
r
dp
r
+
∂ H
∂t
dt (10)
Comparing (8) and (10), we have the relations
∂ H
∂p
r
=˙q
r
,
∂ H
∂q
r
=−˙p
r
(11)
∂ H
∂t
=−
∂ L
∂t
(12)
330 7 Lagrangian and Hamiltonian Mechanics
Equations (11) are called Hamilton’s canonical equations. These are 2n is
number. For a system with n degrees of freedom the n Lagrangian equations
(2) of the second order are replaced by 2n Hamiltonian equations of the first
order. We note from the second equation of (11) that if any coordinate q
l
is not
contained explicitly in the Hamiltonian function H, the conjugate momentum
p
l
is a constant of motion. Such coordinates are called ignorable coordinates.
7.29 The generalized momentum p
r
conjugate to the generalized coordinate q
r
is defined as
∂ L
∂ ˙q
r
= p
r
. If the Lagrangian of a dynamical system does not
contain a certain coordinate, say q
s
, explicitly then p
s
is a constant of motion.
(a) The kinetic energy arises only from the motion of the particle P on the
table as the particle Q is stationary. The potential energy arises from the
particle Q alone.
When P is at distance r from the opening, Q will be at a depth l–x from
the opening:
T =
1
2
mv
2
p
=
1
2
m( ˙r
2
+r
2
˙
θ
2
) (1)
V =−mg(l −r) (2)
L = T − V =
1
2
m( ˙r
2
+r
2
˙
θ
2
) + mg(l −r) (3)
For the two coordinates r and θ , Lagrange’s equations take the form
d
dt
∂ L
∂ ˙r
−
∂ L
∂r
= 0,
d
dt
∂ L
∂
˙
θ
−
∂ L
∂θ
= 0(4)
Equations (4) yield
¨r = r
˙
θ
2
− g (5)
d
dt
(mr
2
˙
θ) = 0
∴ r
2
˙
θ = C = constant (6)
Equations (5) and (6) constitute the equations of motion.
(b) Initial conditions: At r = a, r
˙
θ =
√
ag
∴
˙
θ =
g
a
(7)
Using (7) in (6) with r = a, we obtain
C
2
= a
3
g (8)
7.3 Solutions 331
Using (6) and (8) in (5)
¨r =
rc
2
r
4
− g =
a
3
g
r
3
− g (9)
(c) (i) Since Q does not move, P must be at constant distance r = a from
the opening. Therefore P describes a circle of constant radius a.
(ii) Let P be displaced by a small distance x from the stable circular orbit
of radius a, that is
r = a + x (10)
∴ ¨r =¨x (11)
Using (10) and (11) in (9)
¨x = g
a
3
(a + x)
3
− 1
= g
1 +
x
a
−3
− 1
or ¨x −
3gx
a
or ¨x +
3gx
a
= 0 (12)
which is the equation for simple harmonic motion. Thus the particle P
when slightly displaced from the stable orbit of radius a executes oscilla-
tions around r = a.
This aspect of oscillations has a bearing on the so-called betatron oscil-
lations of ions in circular machines which accelerate charged particles to
high energies. If the amplitudes of the betatron oscillations are large then
they may hit the wall of the doughnut and be lost, resulting in the loss of
intensity of the accelerated particles.
7.30
(i)
x = a cos θ, y = b sin θ, r
2
= a
2
cos
2
θ + b
2
sin
2
θ (1)
˙x =−a
˙
θ sin θ, ˙y = b
˙
θ cos θ (2)
T =
1
2
m( ˙x
2
+˙y
2
) =
1
2
m(a
2
sin
2
θ +b
2
cos
2
θ)
˙
θ
2
(3)
V = mgy +
1
2
kr
2
= mgb sin θ +
1
2
k(a
2
cos
2
θ +b
2
sin
2
θ) (4)
L =
1
2
m(a
2
sin
2
θ +b
2
cos
2
θ)
˙
θ
2
− mgbsin θ
−
1
2
k(a
2
cos
2
θ +b
2
sin
2
θ) (5)
332 7 Lagrangian and Hamiltonian Mechanics
Lagrange’s equation
d
dt
∂ L
∂
˙
θ
−
∂ L
∂θ
= 0
yields
m(a
2
sin
2
θ +b
2
cos
2
θ)
¨
θ +m(a
2
sin θ cos θ − b
2
sin θ cos θ)
˙
θ
2
+ mgbcos θ + k(−a
2
sin θ cos θ + b
2
sin θ cos θ) = 0
or m(a
2
sin
2
θ +b
2
cos
2
θ)
¨
θ −(a
2
− b
2
)(k −m
˙
θ
2
) sin θ cos θ
+ mgbcos θ = 0(6)
(ii) Equilibrium point is located where the force is zero, or ∂ V/∂θ = 0.
Differentiating (4)
∂V
∂θ
= mgb cos θ + k(b
2
− a
2
) sin θ cos θ (7)
Clearly the right-hand side of (7) is zero for θ =±
π
2
Writing (7) as
[mgb + k(b
2
− a
2
) sin θ]cos θ (8)
Another equilibrium point is obtained when
sin θ =
mgb
k(a
2
− b
2
)
(9)
provided a > b.
(iii) An equilibrium point will be stable if
∂
2
V
∂θ
2
> 0 and will be unstable if
∂
2
V
∂θ
2
< 0. Differentiating (8) again we have
∂
2
V
∂θ
2
= k(b
2
− a
2
)(cos
2
θ −sin
2
θ) − mgb sin θ (10)
For θ =
π
2
,(10) reduces to
k(a
2
− b
2
) − mgb (11)
Expression (11) will be positive if a
2
> b
2
+
mgb
k
, and θ =
π
2
will be
a stable point.

7.3 Solutions 333
For θ =−
π
2
,(10) reduces to
k(a
2
− b
2
) + mgb (12)
Expression (12) will be positive if a
2
> b
2
−
mgb
k
, and θ =−
π
2
will be
a stable point.
(iv) T = 2π
A(θ )
V
(θ)
V
−
π
2
= k(a
2
− b
2
) + mgb, by (12)
A(θ ) is the coefficient of
1
2
˙
θ
2
in (3)
∴ A(θ) = m(a
2
sin
2
θ +b
2
cos
2
θ)
∴ A
−
π
2
= ma
2
∴ T = 2π
ma
2
k(a
2
− b
2
) + mgb
7.31 In prob. (7.12) the following equations were obtained:
(m
1
+ m
2
) l
1
¨
θ
1
+ m
2
l
2
¨
θ
2
+ (m
1
+ m
2
)gθ
1
= 0(1)
l
2
¨
θ
2
+ gθ
2
+l
1
¨
θ
1
= 0(2)
For l
1
= l
2
= l and m
1
= m
2
= m,(1) and (2) become
2l
¨
θ
1
+l
¨
θ
2
+ 2gθ
1
= 0(3)
l
¨
θ
2
+l
¨
θ
1
+ gθ
2
= 0(4)
The harmonic solutions of (3) and (4) are written as
θ
1
= A sin ωt,θ
2
= B sin ωt(5)
¨
θ
1
=−Aω
2
sin ωt,
¨
θ
2
=−Bω
2
sin ωt(6)
Substituting (5) and (6) in (3) and (4) and simplifying
2(lω
2
− g)A +lω
2
B = 0(7)
lω
2
A + (lω
2
− g)B = 0(8)
The frequency equation is obtained by equating to zero the determinant
formed by the coefficients of A and B:
334 7 Lagrangian and Hamiltonian Mechanics
2(lω
2
− g) lω
2
lω
2
(lω
2
− g)
= 0
Expanding the determinant
l
2
ω
4
− 4lgω
2
+ 2 g
2
= 0
ω
2
=
2 ±
√
2
g
l
∴ ω =
2 ±
√
2
g
l
∴ ω
1
= 0.76
g
l
,ω
2
= 1.85
g
l
7.32 While the method employed in prob.(6.46) was based on forces or torques,
that is, Newton’s method, the Lagrangian method is based on energy:
T =
1
2
m ( ˙x
2
1
+˙x
2
2
) (1)
For small angles ˙y
1
and ˙y
2
are negligibly small
V =
1
2
k(x
1
− x
2
)
2
+ mgb(1 − cos θ
1
) + mgb(1 − cos θ
2
)
For small angles 1 − cos θ
1
=
θ
2
1
2
=
x
2
1
2b
2
.
Similarly, 1 − cos θ
2
=
x
2
2
2b
2
∴ V =
1
2
k(x
1
− x
2
)
2
+
mg
2b
(x
2
1
+ x
2
2
) (2)
∴ L =
1
2
m( ˙x
2
1
+˙x
2
2
) −
1
2
k(x
2
1
− 2x
1
x
2
+ x
2
2
) −
mg
2b
(x
2
1
− x
2
2
) (3)
The Lagrange’s equations for the coordinates x
1
and x
2
are
d
dt
∂ L
∂ ˙x
1
−
∂ L
∂x
1
= 0,
d
dt
∂ L
∂ ˙x
2
−
∂ L
∂x
2
= 0(4)
Using (3) in (4) we obtain
m ¨x
1
+
k +
mg
b
x
1
− kx
2
= 0(5)
m ¨x
2
− kx
1
+
k +
mg
b
x
2
= 0(6)
7.3 Solutions 335
Assuming that x
1
and x
2
are periodic with the same frequency but different
amplitudes, let
x
1
= A sin ωt, ¨x
1
=−Aω
2
sin ωt(7)
x
2
= B sin ωt, ¨x
2
=−Bω
2
sin ωt(8)
Substituting (7) and (8) in (5) and (6) and simplifying
k +
mg
b
− mω
2
A − kB = 0(9)
− kA+
k +
mg
b
− mω
2
B = 0 (10)
The frequency equation is obtained by equating to zero the determinant
formed by the coefficients of A and B:
k +
mg
b
− mω
2
−k
−k
k +
mg
b
− mω
2
= 0
Expanding the determinant and solving gives
ω
1
=
g
b
and ω
2
=
g
b
+
2k
m
,
In agreement with the results of prob.(6.46).
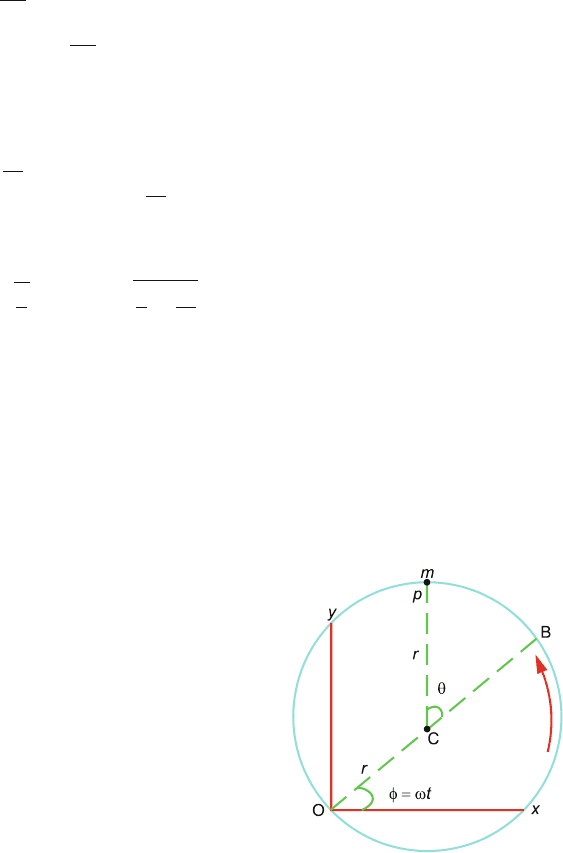
7.33 Let the origin be at the fixed point O and OB be the diameter passing through
C the centre of the circular wire, Fig. 7.30. The position of m is indicated
by the angle θ subtended by the radius CP with the diameter OB. Only one
general coordinate q = θ is sufficient for this problem. Let φ = ωt be the
angle which the diameter OB makes with the fixed x-axis. From the geometry
of the diagram (Fig. 7.30) the coordinates of m are expressed as
Fig. 7.30

336 7 Lagrangian and Hamiltonian Mechanics
x = r cos ωt + r cos (θ + ωt) (1)
y = r sin ωt +r sin (θ + ωt) (2)
The velocity components are found as
˙x =−r ω sin ωt −r(
˙
θ +ω) sin (θ + ωt) (3)
˙y = r ω cos ωt −r(
˙
θ +ω) cos (θ + ωt) (4)
Squaring and adding and simplifying we obtain
˙x
2
+˙y
2
= r
2
ω
2
+r
2
(
˙
θ +ω)
2
+ 2r
2
ω(
˙
θ +ω) cos θ (5)
∴ T =
1
2
mr
2
[ω
2
+ (
˙
θ +ω)
2
+ 2ω(
˙
θ +ω) cos θ ] (6)
Here V = 0, and so L = T . The Lagrange’s equation then simply reduces to
d
dt
∂T
∂
˙
θ
−
∂T
∂θ
= 0(7)
Cancelling the common factor mr
2
(7) becomes
d
dt
(
˙
θ +ω + ω cos θ) +ω(
˙
θ +ω) sin θ = 0(8)
which reduces to
¨
θ +ω
2
sin θ = 0(9)
which is the equation for simple pendulum. Thus the bead oscillates about the
rotating line OB as a pendulum of length r = a/ω
2
.
7.34 (a) The velocity v of mass m relative to the horizontal surface is given by
combining ˙s with ˙x. The components of the velocity v are
v
x
=˙x +˙s cos α (1)
v
y
=−˙s sin α (2)
∴ v
2
= v
2
x
+ v
2
y
=˙x
2
+˙s
2
+ 2 ˙x ˙s cos α (3)
Kinetic energy of the system
T =
1
2
M ˙x
2
+
1
2
m (˙s
2
+˙x
2
+ 2˙s ˙x cos α) (4)
Potential energy comes exclusively from the mass m (spring energy +
gravitational energy)

7.3 Solutions 337
V =
k
2
(s −l)
2
+ mg(h − s sin α) (5)
L = T − V =
(M + m)
2
˙x
2
+
1
2
m ˙s
2
+ m ˙x ˙s cos α −
k
2
(s −l)
2
− mg(h − s sin α) (6)
(b) The generalized coordinates are q
1
= x and q
2
= s. The Lagrange’s
equations are
d
dt
∂ L
∂ ˙x
−
∂ L
∂x
= 0,
d
dt
∂ L
∂ ˙s
−
∂ L
∂s
= 0(7)
Using (6) in (7), equations of motion become
(M + m) ¨x +m¨s cos α = 0(8)
m ¨x cos α + m ¨s + k(s − s
0
) = 0(9)
where s
0
= l + (mg sin α)/k.
Let x = A sin ωt and s − s
0
= B sin ωt (10)
¨x =−ω
2
A sin ωt, ¨s =−Bω
2
sin ωt (11)
Substituting (10) and (11) in (8) and (9) we obtain
A(M + m) + B cos α = 0 (12)
Am ω
2
cos α + B(mω
2
− k) = 0 (13)
Eliminating A and B, we find
ω =
k(M + m)
m(M + m sin
2
α)
(14)
Components of the velocity of the ball as observed on the table are
7.35
v
x
=˙x +˙y cos α (1)
v
y
=˙y sin α (2)
v
2
= v
2
x
+ v
2
y
=˙x
2
+˙y
2
+ 2 ˙x ˙y cos α (3)
T (ball) =
1
2
mv
2
+
1
2
Iω
2
=
1
2
mv
2
+
1
2
×
2
5
mr
2
ω
2
=
1
2
mv
2
+
1
5
mv
2
=
7
10
mv
2
(4)
T (wedge) =
1
2
(M + m) ˙x
2
(5)
