Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.

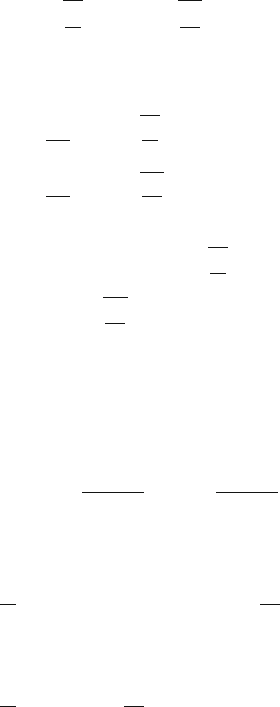
318 7 Lagrangian and Hamiltonian Mechanics
Expanding the determinant
(4k −ω
2
m)
2
− 9k
2
= 0 (13)
This gives the frequencies
ω
1
=
k
m
,ω
2
=
7k
m
(14)
Periods of oscillations are
T
1
=
2π
ω
1
= 2π
m
k
(15)
T
2
=
2π
ω
2
= 2π
m
7k
(16)
If we put ω = ω
1
=
k
m
in (10) or (11) we get A = B and if we put
ω = ω
2
=
7k
m
in (10) or (11), we get A =−B. The first one corresponds to
symmetric mode of oscillation and the second one to asymmetric one.
The normal coordinates q
1
and q
2
are formed by the linear combination of
x and y:
q
1
= x − y, q
2
= x + y (17)
∴ x =
q
1
+q
2
2
, y =
q
2
−q
1
2
(18)
Substituting (18) in (6) and (7)
m
2
( ¨q
1
+¨q
2
) =−2k(q
1
+q
2
) +
3k
2
(q
2
−q
1
) (19)
m
2
( ¨q
2
−¨q
1
) =
3k
2
(q
1
+q
2
) − 2k(q
2
−q
1
) (20)
Adding (19) and (20), m ¨q
2
=−kq
2
(21)
Subtracting (20) from (19), m ¨q
1
=−7kq
1
(22)
Equation (21) is a linear equation in q
2
alone, with constant coefficients. Simi-
larly (22) is a linear equation in q
1
with constant coefficients. Since the coeffi-
cients on the right sides are positive quantities, we note that both (21) and (22)
are differential equations of simple harmonic motion having the frequencies
given in (14). It is the characteristic of normal coordinates that when the equa-

7.3 Solutions 319
tions of motion are expressed in terms of normal coordinates they are linear
with constant coefficients, and each contains but one dependent variable.
Another feature of normal coordinates is that both kinetic energy and
potential energy will have quadratic terms and the cross-products will be
absent. Thus in this example, when (18) is used in (1) and (2) we get the
expressions
T =
m
4
( ˙q
2
1
+˙q
2
2
), V =
k
4
(7q
2
1
+q
2
2
)
The two normal modes are depicted in Fig. 7.22.
(a) Symmetrical with ω
1
=
k
m
and (b) asymmetrical with ω
2
=
7k
m
Fig. 7.22
7.22
(a)
See Fig. 7.23 : T =
1
2
m( ˙x
2
1
+˙x
2
2
) (1)
V =
1
2
kx
2
1
+
1
2
k(x
2
− x
1
)
2
= k
x
2
1
− x
1
x
2
+
1
2
x
2
2
(2)
L = T − V =
1
2
m( ˙x
2
1
+˙x
2
2
) − k
x
2
1
− x
1
x
2
+
1
2
x
2
2
(3)
d
dt
∂ L
∂ ˙x
1
−
∂ L
∂x
1
= 0,
d
dt
∂ L
∂ ˙x
2
−
∂ L
∂x
2
= 0(4)
m ¨x
1
+ k(2x
1
− x
2
) = 0(5)
m ¨x
2
+ k(x
1
− x
1
) = 0(6)
(5) and (6) are equations of motion
(b)
Let the harmonic solutions be x
1
= A sin ωt, x
2
= B sin ωt(7)
Then ¨x
1
=−Aω
2
sin ωt, ¨x
2
=−Bω
2
sin ωt, (8)
Using (7) and (8) in (5) and (6) we get
(2k −mω
2
)A − kB = 0(9)
− kA+(k − mω
2
)B = 0 (10)
Fig. 7.23
320 7 Lagrangian and Hamiltonian Mechanics
The eigenfrequency equation is obtained by equating to zero the determi-
nant formed by the coefficients of A and B:
(2k −mω
2
) −k
−k (k − mω
2
)
= 0 (11)
Expanding the determinant, we obtain
m
2
ω
4
− 3mkω
2
+ k
2
= 0
ω
2
=
3 ±
√
5
2
k
m
(12)
∴ ω
1
= 1.618
k
m
,ω
2
= 0.618
k
m
(13)
(c) Inserting ω = ω
1
in (10) we find B = 1.618 A. This corresponds to a
symmetric mode as both the amplitudes have the same sign.
Inserting ω = ω
2
in (10), we find B =−0.618 A. This corresponds
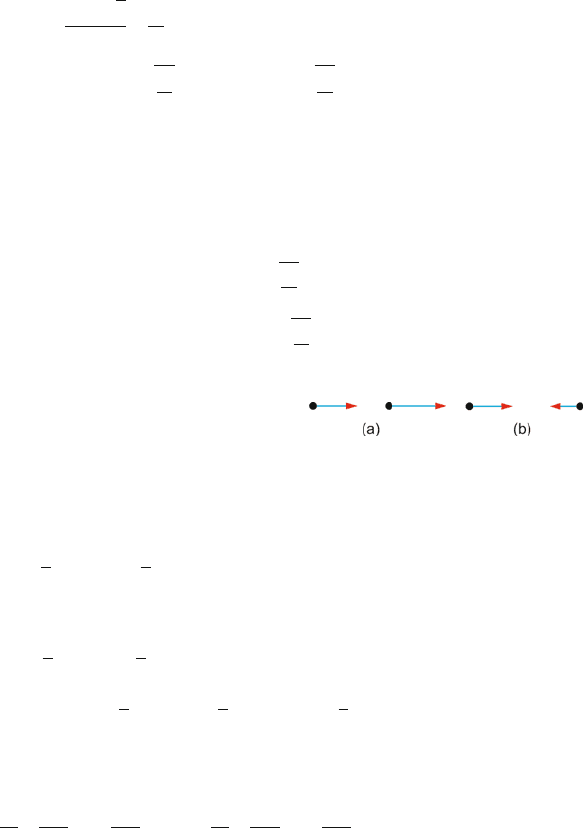
to asymmetric mode. These two modes of oscillation are depicted in
Fig. 7.24 with relative sizes and directions of displacement.
(a) Symmetric mode ω
1
= 1.618
k
m
(b) Asymmetric mode ω
2
= 0.618
k
m
Fig. 7.24
7.23 (a) Let x
1
and x
2
be the displacements of the beads of mass 2m and m,
respectively.
T =
1
2
(2m) ˙x
2
1
+
1
2
(m) ˙x
2
2
(1)
V =
1
2
· 2kx
2
1
+
1
2
k(x
2
− x
1
)
2
(2)
L = m
˙x
2
1
+
1
2
˙x
2
2
− k
3
2
x
2
1
− x
1
x
2
+
1
2
x
2
2
(3)
Lagrange’s equations are
d
dt
∂ L
∂ ˙x
1
−
∂ L
∂x
1
= 0,
d
dt
∂ L
∂ ˙x
2
−
∂ L
∂x
2
= 0(4)

7.3 Solutions 321
which yield equations of motion
2m ¨x
1
+ k(3x
1
− x
2
) = 0(5)
m ¨x
2
− k(x
1
− x
2
) = 0(6)
(b) Let the harmonic solutions be
x
1
= A sin ωt, x
2
= B sin ωt(7)
¨x
1
=−Aω
2
sin ωt, ¨x
2
=−Bω
2
sin ωt(8)
Substituting (7) and (8) in (5) and (6) we obtain
(3k −2mω
2
)A − kB = 0(9)
kA+ (mω
2
− k)B = 0 (10)
The frequency equation is obtained by equating to zero the determinant
formed by the coefficients of A and B:
(3k −2mω
2
) −k
kmω
2
− k
= 0
Expanding the determinant
2m
2
ω
4
− 5km ω
2
+ 2k
2
= 0
ω
1
=
2k
m
,ω
2
=
k
2m
(c) Put ω = ω
1
=
2k
m
in (9) or (10). We find B =−A.
Put ω = ω
2
=
k
2m
in (9) or (10). We find B =+2A.
The two normal modes are sketched in Fig. 7.25.
Fig. 7.25
(a) Asymmetric mode
ω
1
=
2k
m
B =−A

322 7 Lagrangian and Hamiltonian Mechanics
(b) Symmetric mode ω
2
=
k
2m
B =+2A
7.24 There are three coordinates x
1
, x
2
and x
3
,Fig.7.26:
Fig. 7.26
T =
1
2
m ˙x
2
1
+
1
2
Mx
2
2
+
1
2
m ˙x
2
3
(1)
V =
1
2
k
(x
2
− x
1
)
2
+ (x
3
− x
2
)
2
=
1
2
k
x
2
1
− 2x
1
x
2
+ 2x
2
2
− 2x
2
x
3
+ x
2
3
(2)
L =
1
2
m ˙x
2
1
+
1
2
M ˙x
2
2
+
1
2
m ˙x
2
3
−
1
2
k
x
2
1
− 2x
1
x
2
+ 2x
2
2
− 2x
2
x
3
+ x
2
3
(3)
Lagrange’s equations
d
dt
∂ L
∂ ˙x
1
−
∂ L
∂x
1
= 0,
d
dt
∂ L
∂ ˙x
2
−
∂ L
∂x
2
= 0,
d
dt
∂ L
∂ ˙x
3
−
∂ L
∂x
3
= 0(4)
yield
m ¨x
1
+ k(x
1
− x
2
) = 0(5)
M ¨x
2
+ k(−x
1
+ 2x
2
− x
3
) = 0(6)
m ¨x
3
+ k(−x
2
+ x
3
) = 0(7)
Let the harmonic solutions be
x
1
= A sin ωt, x
2
= B sin ωt, x
3
= C sin ωt(8)
∴ ¨x
1
=−Aω
2
sin ωt, ¨x
2
=−Bω
2
sin ωt, ¨x
3
=−Cω
2
sin ωt(9)
Substituting (8) and (9) in (5), (6) and (7)
(k −mω
2
)A − kB = 0 (10)
− kA+(2k − Mω
2
)B − kC = 0 (11)
− kB + (k − mω
2
) C = 0 (12)
7.3 Solutions 323
The frequency equation is obtained by equating to zero the determinant
formed by the coefficients of A, B and C
(k −mω
2
) −k 0
−k (2k − Mω
2
) −k
0 −k (k − mω
2
)
= 0
Expanding the determinant we obtain
ω
2
(k −mω
2
)(ω
2
Mm − 2km − Mk) = 0 (13)
The frequencies are
ω
1
= 0,ω
2
=
k
m
,ω
3
=
k(2m + M)
Mm
(14)
The frequency ω
1
= 0 simply means a translation of all the three particles
without vibration. Ratios of amplitudes of the three particles can be found out
by substituting ω
2
and ω
3
in (10), (11) and (12). Thus when ω = ω
2
k
m
is
substituted in (10), we find the amplitude for the central atom B = 0. When
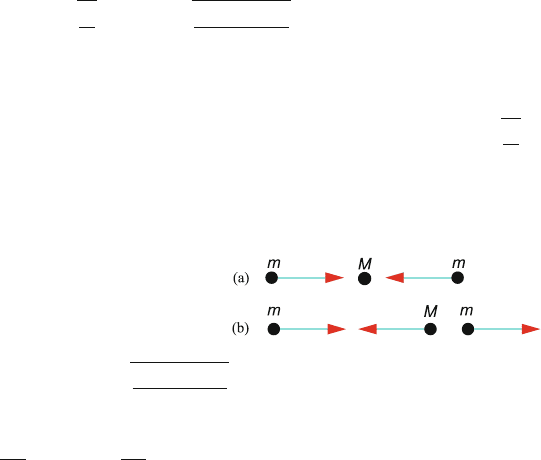
B = 0 is used in (11) we obtain C =−A. This mode of oscillation is depicted
in Fig. 7.27a.
Fig. 7.27
Substituting ω = ω
3
=
k(2m + M)
Mm
in (10) and (12) yields
B =−
2m
M
A =−
2m
M
C
Thus in this mode particles of mass m oscillate in phase with equal amplitude
but out of phase with the central particle.
This problem has a bearing on the vibrations of linear molecules such as
CO
2
. The middle particle represents the C atom and the particles on either side
represent O atoms. Here too there will be three modes of oscillations. One will
have a zero frequency, ω
1
= 0, and will correspond to a simple translation
of the centre of mass. In Fig. 7.27a the mode with ω
1
= ω
2
is such that the
carbon atom is stationary, the oxygen atoms oscillating back and forth in oppo-
site phase with equal amplitude. In the third mode which has frequency ω
3
,
the carbon atom undergoes motion with respect to the centre of mass and is
in opposite phase from that of the two oxygen atoms. Of these two modes

324 7 Lagrangian and Hamiltonian Mechanics
only ω
3
is observed optically. The frequency ω
2
is not observed because in
this mode, the electrical centre of the system is always coincident with the
centre of mass, and so there is no oscillating dipole moment er available.
Hence dipole radiation is not emitted for this mode. On the other hand in the
third mode characterized by ω
3
such a moment is present and radiation is
emitted.
7.25 (a)
y =
x
2
l
(1)
˙y =
2x ·˙x
l
(2)
v
2
=˙x
2
+˙y
2
=˙x
2
1 +
4x
2
l
2
T =
1
2
mv
2
=
1
2
m ˙x
2
1 +
4x
2
l
2
V = mgy =
mgx
2
l
L = T − V =
1
2
m ˙x
2
1 +
4x
2
l
2
−
mgx
2
l
(b)
L =
1
2
m( ˙r
2
+r
2
˙
θ
2
) −U(r)
p
r
=
∂ L
∂ ˙r
= m ˙r, ˙r =
p
r
m
p
θ
=
∂ L
∂
˙
θ
= mr
2
˙
θ,
˙
θ =
p
θ
mr
2
H =
1
2m
p
2
r
+
p
2
θ
r
2
+U(r)
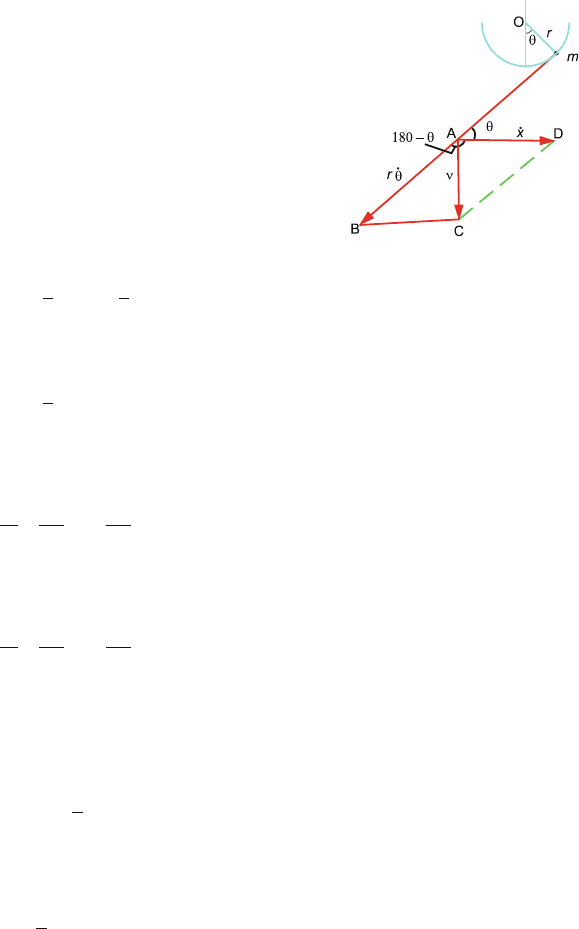
7.26 (a) At any instant the velocity of the block is ˙x on the plane surface. The
linear velocity of the pendulum with respect to the block is l
˙
θ, Fig. 7.28.
The velocity l
˙
θ must be combined vectorially with ˙x to find the velocity
v or the pendulum with reference to the plane:
v
2
=˙x
2
+l
2
˙
θ
2
+ 2 ˙xl
˙
θ cos θ (1)
The total kinetic energy of the system
T =
1
2
M ˙x
2
+
1
2
m( ˙x
2
+l
2
˙
θ
2
+ 2 ˙xl
˙
θ cos θ) (2)
Taking the zero level of the potential energy at the pivot of the pendulum,
the potential energy of the system which comes only from the pendulum is

7.3 Solutions 325
Fig. 7.28
V =−mgl cos θ (3)
∴ L = T − V =
1
2
(M + m) ˙x
2
+ ml cos θ ˙x
˙
θ +
1
2
ml
2
˙
θ
2
+ mgl cos θ
(4)
wherewehaveused(2)and(3).
(b) For small angles cos θ 1−
θ
2
2
, in the first approximation, and cos θ 1,
in the second approximation. Thus in this approximation (4) becomes
L =
1
2
(M + m) ˙x
2
+ ml ˙x
˙
θ +
1
2
ml
2
˙
θ
2
+ mgl
1 −
θ
2
2
(5)
(c) The Lagrange’s equations
d
dt
∂ L
∂
˙
θ
−
∂ L
∂θ
= 0,
d
dt
∂ L
∂ ˙x
−
∂ L
∂x
= 0(6)
lead to the equations of motion
¨x +l
¨
θ + gθ = 0(7)
(M + m) ¨x +ml
¨
θ = 0(8)
(d) Eliminating ¨x between (7) and (8) and simplifying
¨
θ +
(M + m)
M
g
l
θ = 0(9)
This is the equation for angular simple harmonic motion whose frequency
is given by
ω =
(M + m)g
Ml
(10)
326 7 Lagrangian and Hamiltonian Mechanics
7.27
(a) First, we assume that the bowl does not move. Both kinetic energy and
potential energy arise from the particle alone. Taking the origin at O, the
centre of the bowl, Fig. 7.29, the linear velocity of the particle is v = r
˙
θ.
There is only one degree of freedom:
Fig. 7.29
T =
1
2
mv
2
=
1
2
mr
2
˙
θ
2
(1)
V =−mgr cos θ (2)
L =
1
2
mr
2
˙
θ
2
+ mgr cos θ (3)
Lagrange’s equation
d
dt
∂ L
∂ ˙q
−
∂ L
∂q
= 0(4)
becomes
d
dt
∂ L
∂
˙
θ
−
∂ L
∂θ
= 0(5)
which yields the equation of motion
mr
2
¨
θ +mgr sin θ = 0
or
¨
θ +
g
r
sin θ = 0 (equation of motion) (6)
For small angles, sin θ θ . Then (6) becomes
¨
θ +
g
r
θ = 0(7)

7.3 Solutions 327
which is the equation for simple harmonic motion of frequency ω =
g
r
or time period
T =
2π
ω
= 2π
r
g
(8)
(b) (i) The bowl can now slide freely along the x-direction with velocity ˙x.
The velocity of the particle with reference to the table is obtained by
adding l
˙
θ to ˙x vectorially, Fig. 7.29. The total kinetic energy then comes
from the motion of both the particle and the bowl. The potential energy,
however, is the same as i n (a):
v
2
= r
2
˙
θ
2
+ x
2
− 2r
˙
θ ˙x cos(180 − θ) (9)
from the diagonal AC of the parallelogram ABCD
T =
1
2
M ˙x
2
+
1
2
m (r
2
˙
θ
2
+˙x
2
− 2r ˙x
˙
θ cos θ) (10)
V =−mgr cos θ (11)
L = T − V (Lagrangian)
=
1
2
M ˙x
2
+
1
2
m(r
2
˙
θ
2
+˙x
2
− 2r ˙x
˙
θ cos θ) + mgr cos θ (12)
(ii) and (iii).
In the small angle approximation the cos θ in the kinetic energy can be
neglected as cos θ → 1 but can be retained in the potential energy in order
to avoid higher order terms.
Equation (12) then becomes
L =
1
2
(M + m) ˙x
2
− mr ˙x
˙
θ +
1
2
mr
2
˙
θ
2
+ mgr cos θ (13)
We have now two degrees of freedom, x and θ , and the corresponding
Lagrange’s equations are
d
dt
∂ L
∂ ˙x
−
∂ L
∂x
= 0,
d
dt
∂ L
∂
˙
θ
−
∂ L
∂θ
= 0 (14)
