Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.

298 7 Lagrangian and Hamiltonian Mechanics
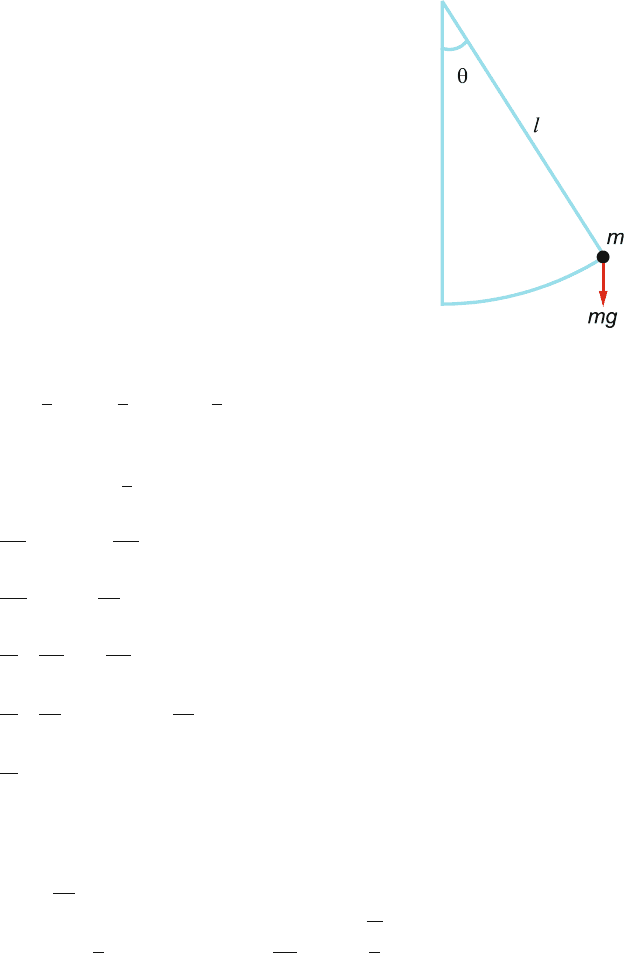
7.2 The position of the pendulum is determined by a single coordinate θ and so we
take q = θ . Then (Fig. 7.13)
Fig. 7.13
T =
1
2
mv
2
=
1
2
mω
2
l
2
=
1
2
ml
2
˙
θ
2
(1)
V = mgl(1 − cos θ) (2)
L = T − V =
1
2
ml
2
˙
θ
2
− mgl (1 −cos θ) (3)
∂T
∂
˙
θ
= ml
2
˙
θ,
∂T
∂θ
= 0(4)
∂V
∂
˙
θ
= 0,
∂
∂θ
= mgl sin θ (5)
d
dt
∂ L
∂
˙
θ
−
∂ L
∂θ
= 0(6)
d
dt
∂
∂
˙
θ
(T − V )
−
∂
∂θ
(T − V ) = 0
d
dt
(ml
2
˙
θ) + mgl sin θ = 0
or l
¨
θ + g sin θ = 0 (equation of motion)
For small oscillation angles sin θ → θ
¨
θ =−
gθ
l
(equation for angular SHM)
∴ ω
2
=
g
l
or time period T =
2π
ω
= 2π
l
g
7.3 Solutions 299
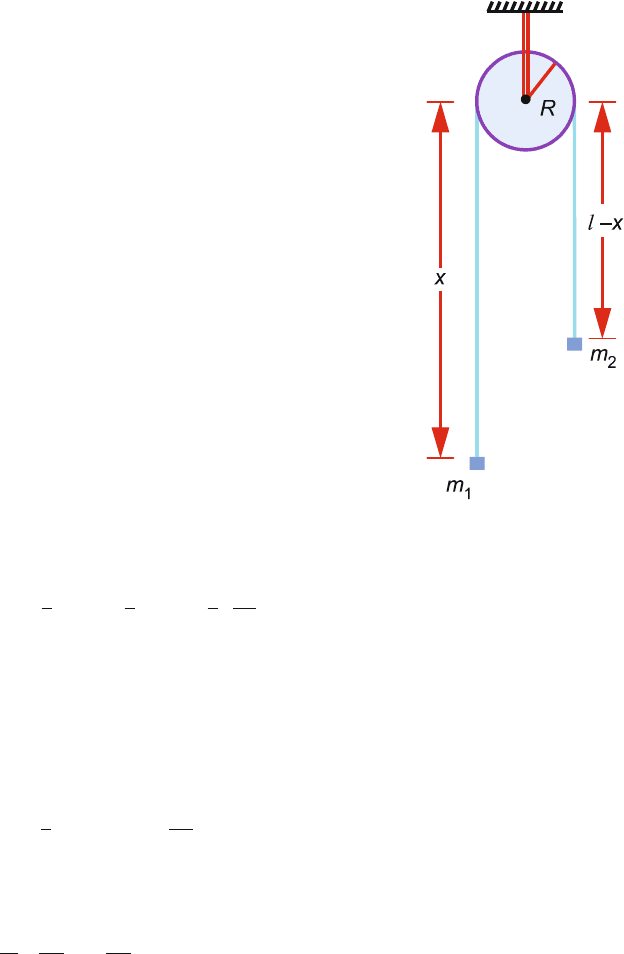
7.3 In this system there is only one degree of freedom. The instantaneous configu-
ration is specified by q = x. Assuming that the cord does not slip, the angular
velocity of the pulley is ˙x/R,Fig.7.14.
Fig. 7.14
The kinetic energy of the system is given by
T =
1
2
m
1
˙x
2
+
1
2
m
2
˙x
2
+
1
2
I
˙x
2
R
2
(1)
The potential energy of the system is
V =−m
1
gx −m
2
g(l − x) (2)
And the Lagrangian is
L =
1
2
m
1
+ m
2
+
I
R
2
˙x
2
+ (m
1
− m
2
)gx + m
2
gl (3)
The equation of motion
d
dt
∂ L
∂ ˙x
−
∂ L
∂x
= 0(4)
300 7 Lagrangian and Hamiltonian Mechanics
yields
m
1
+ m
2
+
I
R
2
¨x − g(m
1
− m
2
) = 0
or ¨x =
(m
1
− m
2
)g
m
1
+ m
2
+
I
R
2
(5)
which is identical with the one obtained by Newton’s mechanics.
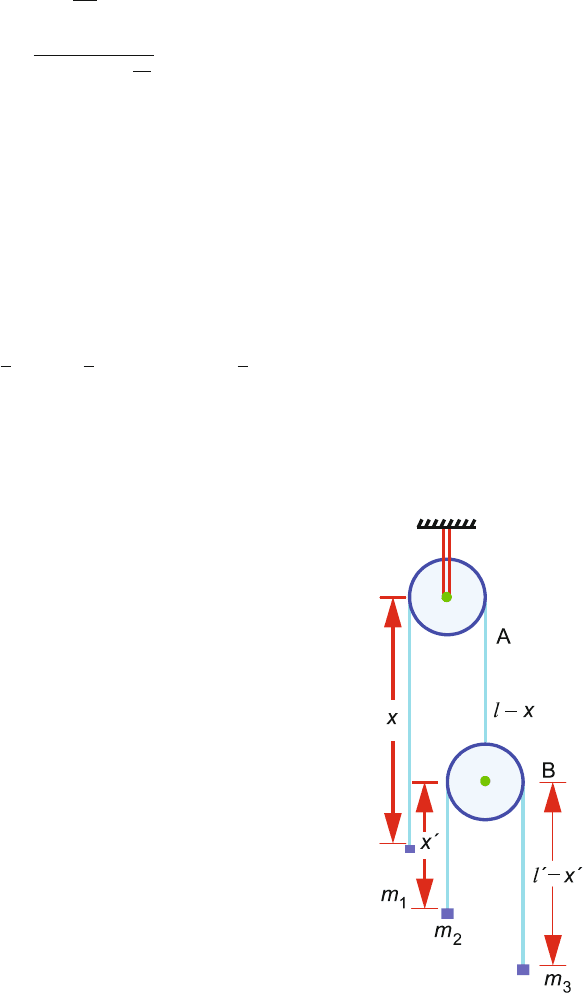
7.4 By problem the masses of pulleys are negligible. The double machine is an
Atwood machine in which one of the weights is replaced by a second Atwood
machine, Fig. 7.15. The system now has two degrees of freedom, and its instan-
taneous configuration is specified by two coordinates x and x
. l and l
denote
the length of the vertical parts of the two strings. Mass m
1
is at depth x below
the centre of pulley A, m
2
at depth l − x + x
and m
3
at depth l + l
− x − x
.
The kinetic energy of the system is given by
T =
1
2
m
1
˙x
2
+
1
2
m
2
(−˙x +˙x
)
2
+
1
2
m
3
(−˙x −˙x
)
2
(1)
while the potential energy is given by
V =−m
1
gx −m
2
g(l − x + x
) − m
3
g(l − x +l
− x
) (2)
Fig. 7.15
7.3 Solutions 301
The Lagrangian of the system takes the form
L =T − V =
1
2
m
1
˙x
2
+
1
2
m
2
(−˙x +˙x
)
2
+
1
2
m
3
(−˙x −˙x
)
2
+ (m
1
− m
2
− m
3
)gx + (m
2
− m
3
)gx + m
2
gl + m
3
g(l + l
) (3)
The equations of motion are then
d
dt
∂ L
∂ ˙x
−
∂ L
∂x
= 0(4)
d
dt
∂ L
∂ ˙x
−
∂ L
∂x
= 0(5)
which yield
(m
1
+ m
2
+ m
3
) ¨x + (m
3
− m
2
) ¨x
= (m
1
− m
2
− m
3
)g (6)
(m
3
− m
2
) ¨x + (m
2
+ m
3
) ¨x
= (m
2
− m
3
)g (7)
Solving (6) and (7) we obtain the equations of motion.
7.5
T = v
2
˙u
2
+ 2˙v
2
(1)
V = u
2
− v
2
(2)
L = T − V = v
2
˙u
2
+ 2˙v
2
− u
2
+ v
2
(3)
∂ L
∂ ˙u
= 2v
2
˙u,
∂ L
∂u
=−2u (4)
∂ L
∂ ˙v
= 4 ˙v,
∂ L
∂v
= 2v( ˙u
2
+ 1) (5)
The equations of motion
d
dt
∂ L
∂ ˙u
−
∂ L
∂u
= 0(6)
d
dt
∂ L
∂ ˙v
−
∂ L
∂v
= 0(7)
yield
2
d
dt
(v
2
˙u) + 2u = 0
or v
2
¨u + 2 ˙u ˙v + 2u = 0(8)
2¨v +v(˙u
2
+ 1) = 0(9)

302 7 Lagrangian and Hamiltonian Mechanics
7.6 Here we need a single coordinate q = x:
T =
1
2
m ˙x
2
, V =
1
2
kx
2
(1)
L =
1
2
m ˙x
2
−
1
2
kx
2
(2)
∂ L
∂ ˙x
= m ˙x,
∂ L
∂x
=−kx (3)
d
dt
∂ L
∂ ˙x
−
∂ L
∂x
= 0(4)
m ¨x +kx = 0(5)
Let x = A sin ωt(6)
¨x =−Aω
2
sin ωt(7)
Inserting (6) and (7) and simplifying
− mω
2
+ k = 0
ω =
k
m
or T
0
=
2π
ω
= 2π
m
k
where T
0
is the time period.
7.7 Only one coordinate q = x (distance on the surface of the incline) is adequate
to describe the motion:
T =
1
2
m ˙x
2
, V =−mgx sin α, L =
1
2
m ˙x
2
+ mgx sin α
∂ L
∂ ˙x
= m ˙x,
∂ L
∂x
= mg sin α
Equation of motion
d
dt
∂ L
∂ ˙q
−
∂ L
∂q
= 0
yields
d
dt
(m ˙x) −
∂
∂x
(mgx sin α) = 0
or ¨x = g sin α
7.8 This is a two degree of freedom system because both mass m and M are mov-
ing. The coordinate on the horizontal axis is described by x
for the inclined
plane and x for the block of mass m on the incline. The origin of the coordinate
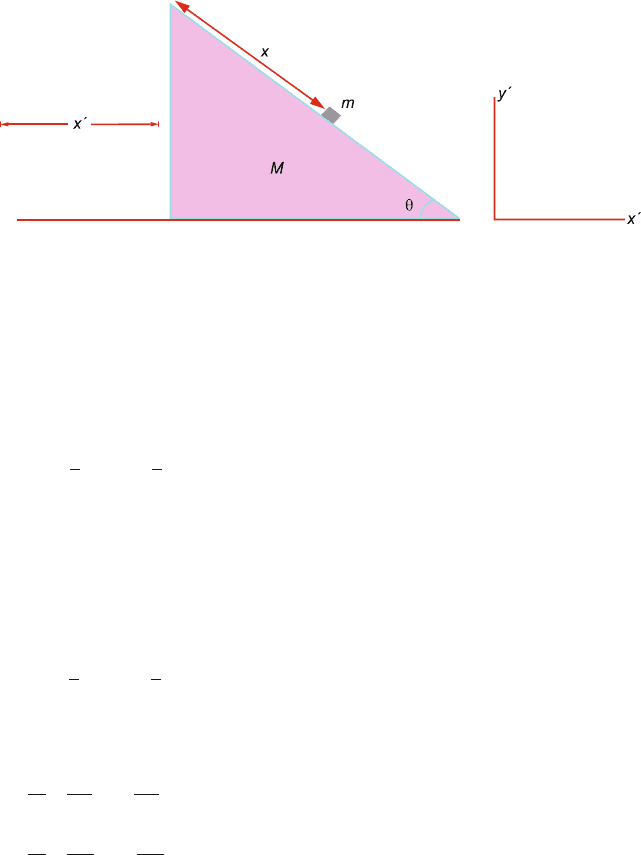
7.3 Solutions 303
system is fixed on the smooth table, Fig. 7.16.Thex- and y-components of the
velocity of the block are given by
Fig. 7.16
v
x
=˙x
+˙x cos θ (1)
v
y
=−˙x sin θ (2)
∴ v
2
= v
2
x
+ v
2
y
=˙x
2
+ 2 ˙x ˙x
cos θ +˙x
2
(3)
Hence, the kinetic energy of the system will be
T =
1
2
M ˙x
2
+
1
2
m( ˙x
2
+ 2 ˙x ˙x
cos θ +˙x
2
) (4)
while the potential energy takes the form
V =−mgx sin θ (5)
and the Lagrangian is given by
L =
1
2
M ˙x
2
+
1
2
m( ˙x
2
+ 2 ˙x ˙x
cos θ +˙x
2
) + mgx sin θ (6)
The equations of motion
d
dt
∂ L
∂ ˙x
−
∂ L
∂x
= 0(7)
d
dt
∂ L
∂ ˙x
−
∂ L
∂x
= 0(8)
yield
m( ¨x
cos θ +¨x) − mg sin θ = 0(9)
M ¨x
+ m( ¨x
+¨x cos θ) = 0 (10)
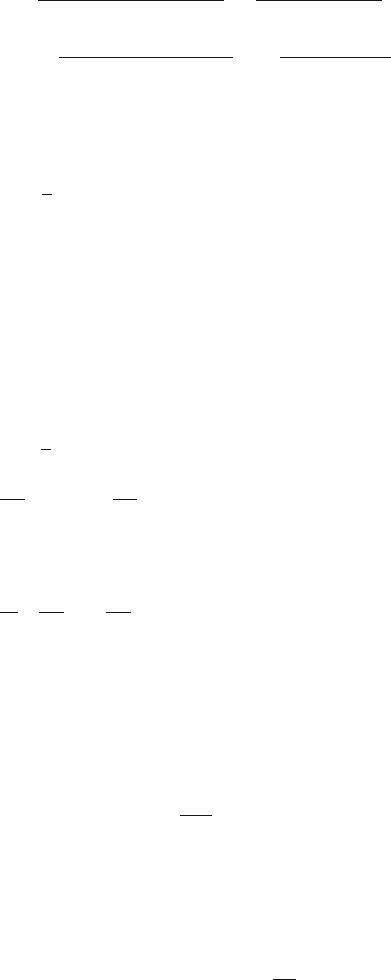
304 7 Lagrangian and Hamiltonian Mechanics
Solving (9) and (10)
¨x =
g sin θ
1 − m cos
2
θ/(M + m)
=
(M + m)g sin θ
M + m sin
2
θ
(11)
¨x
=−
g sin θ cos θ
(M + m)/m −cos
2
θ
=−
mg sin θ cos θ
M + m sin
2
θ
(12)
which are in agreement with the equations of prob. (2.14) derived from Newto-
nian mechanics.
7.9
T =
1
2
m( ˙x
2
+ ω
2
x
2
) (1)
because the velocity of the bead on the wire is at right angle to the linear veloc-
ity of the wire:
V = mgx sin ωt(2)
because ωt = θ, where θ is the angle made by the wire with the horizontal at
time t, and x sin θ is the height above the horizontal position:
L =
1
2
m( ˙x
2
+ ω
2
x
2
) − mgx sin ωt (3)
∂ L
∂ ˙x
= m ˙x,
∂ L
∂x
= mω
2
x − mg sin ωt (4)
Lagrange’s equation
d
dt
∂ L
∂ ˙x
−
∂ L
∂x
(5)
then becomes
¨x −ω
2
x + g sin ωt = 0 (equation of motion) (6)
which has the solution
x = Ae
ωt
+ Be
−ωt
+
g
2ω
2
sin ωt(7)
where A and B are constants of i ntegration which are determined from initial
conditions.
At t = 0, x = 0 and ˙x = 0(8)
Further ˙x = ω(Ae
ωt
− Be
−ωt
) +
g
2ω
cos ωt(9)
7.3 Solutions 305
Using (8) in (7) and (9) we obtain
0 = A + B (10)
0 = ω(A − B) +
g
2ω
(11)
Solving (10) and (11) we get A =−
g
4ω
2
, B =
g
4ω
2
(12)
The complete solution for x is
x =
g
4ω
2
(e
−ωt
− e
ωt
+ 2sinωt)
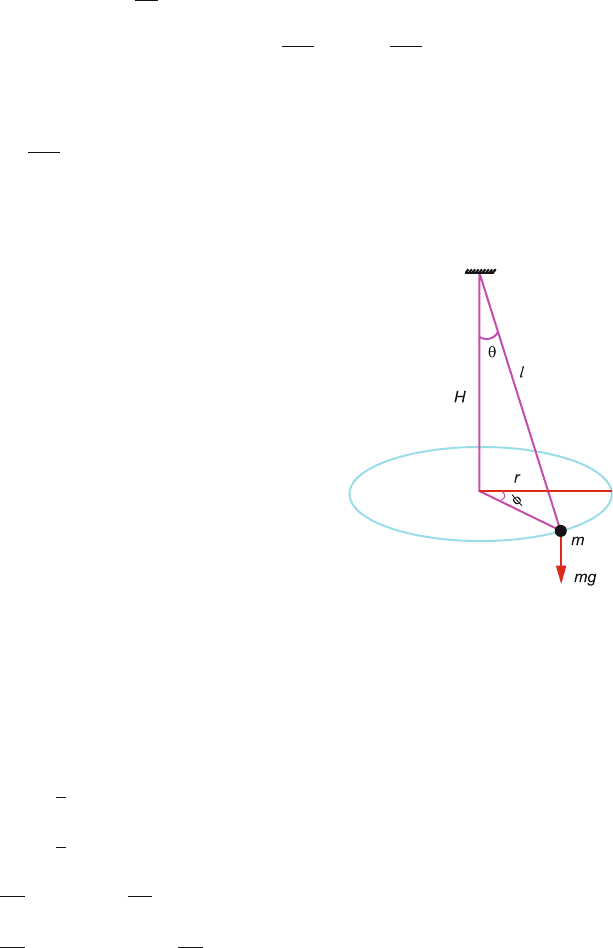
7.10 Let the length of the cord be l. The Cartesian coordinates can be expressed in
terms of spherical polar coordinates (Fig. 7.17)
Fig. 7.17
x = l sin θ cos φ
y = l sin θ sin φ
z =−l cos θ
V = mgz =−mgl cos θ (1)
v
2
=˙x
2
+˙y
2
+˙z
2
= l
2
(
˙
θ
2
+ sin
2
θ
˙
φ
2
)
T =
1
2
ml
2
(
˙
θ
2
+ sin
2
θ
˙
φ
2
) (2)
L =
1
2
ml
2
(
˙
θ
2
+ sin
2
θ
˙
φ
2
) + mgl cos θ (3)
∂ L
∂
˙
θ
= ml
2
˙
θ,
∂ L
∂θ
= ml
2
sin θ cos θ
˙
φ
2
− mgl sin θ (4)
∂ L
∂
˙
φ
= ml
2
sin
2
θ
˙
φ,
∂ L
∂φ
= 0(5)

306 7 Lagrangian and Hamiltonian Mechanics
The Lagrangian equations of motion
d
dt
∂ L
∂
˙
θ
−
∂ L
∂θ
= 0 and
d
dt
∂ L
∂
˙
φ
−
∂ L
∂φ
= 0(6)
give
¨
θ −sin θ cos θ
˙
φ
2
+
g
l
sin θ = 0(7)
ml
2
d
dt
(sin
2
θ
˙
φ) = 0(8)
Hence sin
2
θ
˙
φ = constant = C (9)
and eliminating
˙
φ in (7) with the use of (9) we get a differential equation in θ
only.
¨
θ +
g
l
sin θ − C
2
cos θ
sin
3
θ
= 0 (10)
The quantity P
φ
=
∂ L
∂
˙
φ
= ml
2
sin
2
θ
˙
φ (5)
is a constant of motion and is recognized as the angular momentum of the
system about the z-axis. It is conserved because torque is not produced either
by gravity or the tension of the cord about the z-axis. Thus conservation of
angular momentum is reflected in (5).
Two interesting cases arise. Suppose φ = constant. Then
˙
φ = 0 and C = 0.
In this case (10) reduces to
¨
θ +
g
l
sin θ = 0 (11)
which is appropriate for simple pendulum in which the bob oscillates in the
vertical plane.
Suppose θ = constant, then from (9)
˙
φ = constant. Putting
¨
θ = 0in(7)
we get
ω =
˙
φ =
g
l cos θ
=
g
H
(12)
and time period
T =
2π
ω
=
H
g
(13)
appropriate for the conical pendulum in which the bob rotates on horizontal
plane with uniform angular velocity with the cord inclined at constant angle θ
with the vertical axis.
7.3 Solutions 307
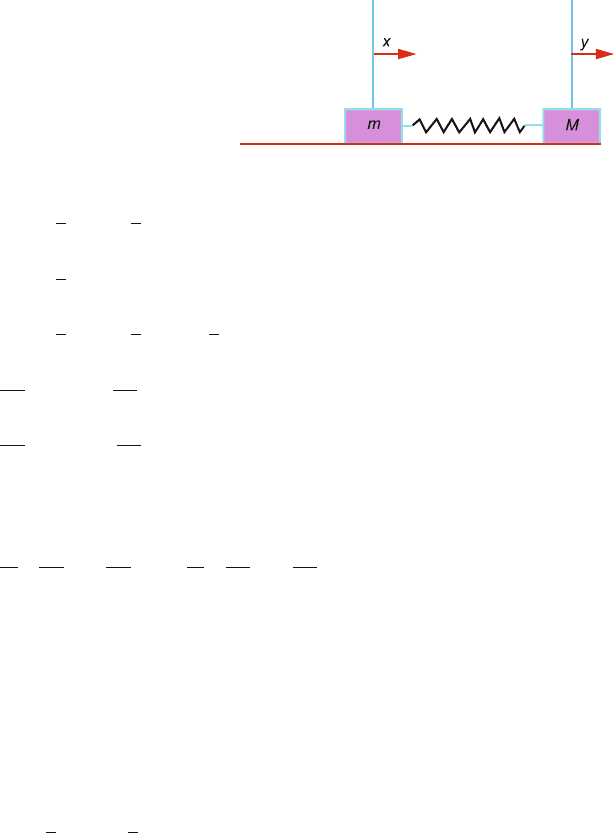
7.11 The two generalized coordinates x and y are indicated in Fig. 7.18. The kinetic
energy of the system comes from the motion of the blocks and potential energy
from the coupling spring:
Fig. 7.18
T =
1
2
m ˙x
2
+
1
2
M ˙y
2
(1)
V =
1
2
k(x − y)
2
(2)
L =
1
2
m ˙x
2
+
1
2
M ˙y
2
−
1
2
k(x − y)
2
(3)
∂ L
∂ ˙x
= m ˙x,
∂ L
∂x
=−k(x − y) (4)
∂ L
∂ ˙y
= M ˙y,
∂ L
∂y
= k(x − y) (5)
Lagrange’s equations are written as
d
dt
∂ L
∂ ˙x
−
∂ L
∂x
= 0,
d
dt
∂ L
∂ ˙y
−
∂ L
∂y
= 0(6)
Using (4) and (5) in (6) we obtain the equations of motion
m ¨x +k(x − y) = 0(7)
m ¨y + k(y − x) = 0(8)
7.12 This problem involves two degrees of freedom. The coordinates are θ
1
and θ
2
(Fig. 7.19)
T =
1
2
m
1
v
2
1
+
1
2
m
2
v
2
2
(1)
v
2
1
= (l
1
˙
θ
1
)
2
(2)
v
2
2
= (l
1
˙
θ
1
)
2
+ (l
2
˙
θ
2
)
2
+ 2l
1
l
2
˙
θ
1
˙
θ
2
cos(θ
2
− θ
1
) (by parallelogram law) (3)
For small angles, cos(θ
2
− θ
1
) 1
