Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.

268 6 Oscillations
d
2
θ
dt
2
+
MgD
I
θ = 0(3)
d
2
θ
dt
2
+
3
2
g
L
θ = 0
ω
2
=
3
2
g
L
T =
2π
ω
= 2π
2L
3g
(4)
For a simple pendulum
T = 2π
l
g
(5)
Comparing (4) and (5), the equivalent length of a simple pendulum is l =
2
3
L.
6.33 From the results of prob. (6.31) the time period of a physical pendulum is
given by
T = 2π
I
MgD
(1)
where I is the moment of inertia about the pivot A, Fig. 6.9.
Now I = I
C
+ MD
2
and I
C
= Mk
2
(2)
where k is the radius of gyration. Formula (1) then becomes
T = 2π
k
2
+ D
2
gD
(3)
and the length of the simple equivalent pendulum is D +
k
2
D
.
If a point B be taken on AG such that AB = D +
k
2
D
, A and B are known as
the centres of suspension and oscillation, respectively. Here G is the centre of
mass (CM) of the physical pendulum.
Suppose now the body is suspended at B, then the time of oscillation is
obtained by substituting
k
2
D
for D in the expression
6.3 Solutions 269
2π
k
2
+ D
2
gD
and is therefore 2π
k
2
+
k
4
D
2
g
k
2
D
i.e. 2π
D
2
+ k
2
gD
Thus the centres of suspension and oscillation are convertible, for if the
body be suspended from either it will make small vibrations in the same
time as a simple pendulum whose length L is the distance between these
centres.
T = 2π
L
g
or g =
4π
2
L
T
2
6.34
ω =
mgd
I
(1)
d =
4R
3π
(2)
the distance of the point of suspension from the centre of mass
I =
mR
2
2
(3)
Substituting (2) and (3) in (1) and simplifying
ω =
8g
3π R
6.35
T = 2π
I
mgd
T
1
= 2π
mr
2
+ mr
2
mgr
= 2π
2r
g
T
2
= 2π
1
2
mr
2
+ mr
2
mgr
= 2π
3
2
r
g
∴
T
1
T
2
=
4
3
=
2
√
3
6.36 In Fig. 6.20 OA is the reference line or the disc in the equilibrium position. If
the disc is rotated in the horizontal plane so that the reference line occupies
the line OB, the wire would have twisted through an angle θ. The twisted wire
will exert a restoring torque on the disc causing the reference line to move to
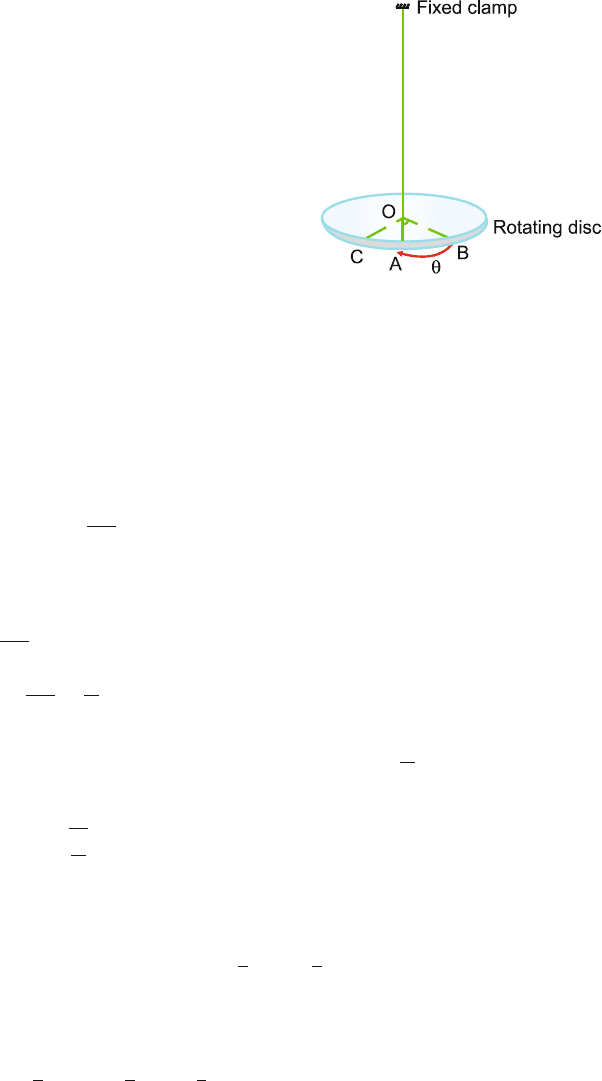
270 6 Oscillations
Fig. 6.20
its original position. For small twists the r estoring torque will be proportional
to the angular displacement in accordance with Hooke’s law.
τ =−Cθ (1)
where C is known as torsional constant. If I is the moment of inertia of the
disc about its axis, α the angular acceleration, the torque τ is given by
τ = Iα = I
d
2
θ
dt
2
(2)
Comparing (1) and (2)
I
d
2
θ
dt
2
=−Cθ
or
d
2
θ
dt
2
+
C
I
θ = 0(3)
which is the equation for angular SHM with ω
2
=
C
I
. Time period for small
oscillations is given by
T = 2π
I
C
(4)
6.37 Total kinetic energy of the system
K = K (mass) + K (pulley) =
1
2
m ˙x
2
+
1
2
I
˙
θ
2
Replacing x by rθ and ˙x by r
˙
θ
K =
1
2
mr
2
˙
θ
2
+
1
2
I
˙
θ
2
=
1
2
(mr
2
+ I)
˙
θ
2

6.3 Solutions 271
Potential energy of the spring
U =
1
2
kx
2
=
1
2
kr
2
θ
2
Total energy
E = K + U =
1
2
(mr
2
+ I)
˙
θ
2
+
1
2
kr
2
θ
2
= constant
Differentiating with respect to time
dE
dt
= (mr
2
+ I)
˙
θ ·
¨
θ +kr
2
θ ·
˙
θ = 0
Cancelling
˙
θ
¨
θ +
kr
2
θ
mr
2
+ I
= 0
which is the equation for angular SHM with
ω
2
=
kr
2
mr
2
+ I
. Therefore
ω =
kr
2
mr
2
+ I
6.38 Let at any instant the centre of the cylinder be displaced by x towards right.
Then the spring at C is compressed by x while the spring at P is elongated by
2x.Ifv =˙x is the velocity of the centre of mass of the cylinder and ω =
˙
θ its
angular velocity, the total energy in the displaced position will be
E =
1
2
m ˙x
2
+
1
2
I
C
˙
θ
2
+
1
2
k
1
x
2
+
1
2
k
2
(2x)
2
(1)
Substituting x = rθ, ˙x = r
˙
θ, and I
C
=
1
2
mr
2
, where r is the radius of the
cylinder, (1) becomes
E =
3
4
mr
2
˙
θ
2
+
1
2
r
2
(k
1
+ 4k
2
)θ
2
= constant
dE
dt
=
3
2
mr
2
˙
θ
¨
θ +r
2
(k
1
+ 4k
2
)θ
˙
θ = 0
∴
¨
θ +
2
3m
(k
1
+ 4k
2
)θ = 0
272 6 Oscillations
which is the equation for angular SHM with ω
2
=
2
3m
(k
1
+ 4k
2
).
T =
2π
ω
= 2π
3m
2(k
1
+ 4k
2
)
6.39
U(x) =
a
x
2
−
b
x
Equilibrium position is obtained by minimizing the function U(x).
dU
dx
=−
2a
x
3
+
b
x
2
= 0
x = x
0
=
2a
b
Measuring distances from the equilibrium position and replacing x by x +
2a
b
F =−
dU
dx
=
2a
x
3
−
b
x
2
F =
2a
(x + 2a/b)
3
−
b
(x + 2a/b)
2
=
2a
(2a/b)
3
1 +
bx
2a
−3
−
b
(2a/b)
2
1 +
bx
2a
−2
Since the quantity bx /2a is assumed to be small, use binomial expansion
retaining terms up to linear in x.
F =−
b
4
x
8a
3
Acceleration a =
F
m
=−
b
4
x
8a
3
m
=−ω
2
x
where ω =
b
4
8a
3
m
T =
2π
ω
= 4π
2ma
2
b
4
6.3 Solutions 273
6.3.3 Coupled Systems of Masses and Springs
6.40 Let spring 1 undergo an extension x
1
due to force F. Then x
1
=
F
k
1
. Similarly,
for spring 2, x
2
=
F
k
2
.
The force is the same in each spring, but the total displacement x is the sum
of individual displacements:
x = x
1
+ x
2
=
F
k
1
+
F
k
2
k
eq
=
F
x
=
F
x
1
+ x
2
=
F
F
k
1
+
F
k
2
=
1
1
k
1
+
1
k
2
=
k
1
k
2
k
1
+ k
2
∴ T = 2π
m
k
eq
= 2π
(k
1
+ k
2
)m
k
1
k
2
6.41 The displacement is the same for both the springs and the total force is the
sum of individual forces.
F
1
= k
1
x, F
2
= k
2
x
F = F
1
+ F
2
= (k
1
+ k
2
)x
k
eq
=
F
x
= k
1
+ k
2
T = 2π
m
k
eq
= 2π
m
k
1
+ k
2
6.42 Let the centre of mass be displaced by x. Then the net force
F =−k
1
x − k
2
x =−(k
1
+ k
2
)x
Acceleration a =
F
m
=−(k
1
+ k
2
)
x
m
=−ω
2
x
T =
2π
ω
= 2π
m
k
1
+ k
2
6.43 Spring constant of the wire is given by
k
=
YA
L
(1)
274 6 Oscillations
Since the spring and the wire are in series, the effective spring constant k
eff
is
given by
k
eff
=
k
k
k +k
(2)
The time period of oscillations is given by
T = 2π
m
k
eff
(3)
Combining (1), (2) and (3)
T = 2π
m(YA+kL)
YAk
6.44 In Fig. 6.15, C is the point of contact around which the masses M and m rotate.
As it is the instantaneous centre of zero velocity, the equation of motion is of
the form τ
c
= I
c
¨
θ, where I
c
is the moment of inertia of masses M and m
with respect to point C. Now
I
c
=
1
2
MR
2
+ MR
2
+ md
2
(1)
where d
2
= L
2
+ R
2
− 2RL cos θ. (2)
For small oscillations, sin θ θ , cos θ 1 and
I
c
=
3MR
2
2
+ m(L −d)
2
(3)
Therefore the equation of motion become
3MR
2
2
+ m(L − d)
2
¨
θ =−mg L sin θ =−mg Lθ
or
¨
θ +
mg L
3MR
2
/2 + m(L − d)
2
θ = 0
∴ ω =
mg L
3MR
2
/2 + m(L − d)
2
rad/s
6.45 Figure 6.21 shows the semicircular disc tilted through an angle θ compared to
the equilibrium position (b). G is the centre of mass such that a = OG =
4r
3π
,
where r is the radius.
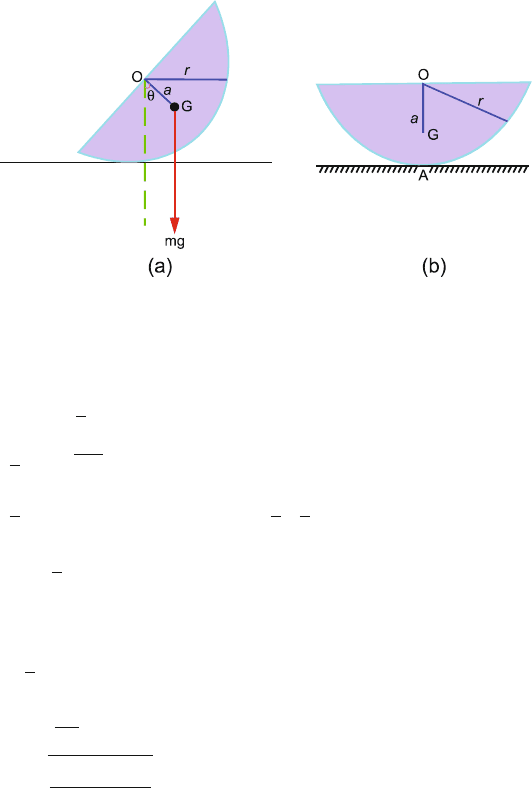
6.3 Solutions 275
Fig. 6.21
We use the energy method.
K (max) =
1
2
I
A
ω
2
=
1
2
(I
G
+ GA
2
)ω
2
=
1
2
[I
0
− ma
2
+ m(r − a)
2
]ω
2
=
1
2
1
2
mr
2
+ mr(r − 2a)
ω
2
= mr
3
4
r −a
ω
2
K
max
= U
max
mr
3
4
r −a
ω
2
= mga(1 − cos θ)
But a =
4r
3π
ω = 4
(1 − cos θ)g
(9π −16)r
6.46 Referring to Fig. 6.16, take torques about the two hinged points P and Q.
mb
2
¨
θ
1
=−mgbθ
1
− kb
2
(θ
1
− θ
2
)
The left side gives the net torque which is the product of moment of inertia
about P and the angular acceleration. The first term on the right side gives
the torque of the force mg, which is force times the perpendicular distance
from the vertical through P. The second term on the right side is the torque
produced by the spring which is k(x
1
− x
2
) times the perpendicular distance

276 6 Oscillations
from P, that is, k(x
1
− x
2
)b or k(θ
1
− θ
2
)b
2
. The second equation of motion
can be similarly written. Thus, the two equations of motion are
mb
¨
θ
1
+ mgθ
1
+ kb(θ
1
− θ
2
) = 0(1)
mb
¨
θ
2
+ mgθ
2
+ kb(θ
2
− θ
1
) = 0(2)
The harmonic solutions are
θ
1
= A sin ωt,θ
2
= B sin ωt (3)
¨
θ
1
=−Aω
2
sin ωt,
¨
θ
2
=−Bω
2
sin ωt (4)
Substituting (3) and (4) in (1) and (2) and simplifying
(mg +kb − mbω
2
)A − kb B = 0(5)
− kb A + (mg + kb − mbω
2
)B = 0(6)
The frequency equation is obtained by equating to zero the determinant
formed by the coefficients of A and B.
mg +kb − mbω
2
−kb
−kb
mg +kb − mbω
2
= 0
Expanding the determinant and solving for ω we obtain
ω
1
=
g
b
,ω
2
=
g
b
+
2k
m
6.47 In prob. (6.46) equations of motion (1) and (2) can be re-written in terms of
Cartesian coordinates x
1
and x
2
since x
1
= bθ
1
and x
2
= bθ
2
.
m ¨x
1
+
mgx
1
b
+ k(x
1
− x
2
) = 0(1)
m ¨x
2
+
mgx
2
b
+ k(x
2
− x
1
) = 0(2)
It is possible to make linear combinations of x
1
and x
2
such that a combination
involves but a single frequency. These new coordinates X
1
and X
2
, called
normal coordinates, vary harmonically with but a single frequency. No energy
transfer occurs from one normal coordinate to another. They are completely
independent.
x
1
=
X
1
+ X
2
2
, x
2
=
X
1
− X
2
2
(3)
6.3 Solutions 277
Substituting (3) in (1) and (2)
m
2
(
¨
X
1
+
¨
X
2
) +
mg
2b
(X
1
+ X
2
) + kX
2
= 0(4)
m
2
(
¨
X
1
−
¨
X
2
) +
mg
2b
(X
1
− X
2
) − kX
2
= 0(5)
Adding (4) and (5)
m
¨
X
1
+
mg
b
X
1
= 0(6)
which is a linear equation in X
1
alone with constant coefficients.
Subtracting (5) from (4), we obtain
m
¨
X
2
+
mg
b
+ 2k
X
2
= 0(7)
This is again a linear equation in X
2
as the single dependent variable. Since
the coefficients of X
1
and X
2
are positive, both (6) and (7) are differential
equations of simple harmonic motion having frequencies ω
1
=
g
b
and
ω
2
=
g
b
+
2k
m
. Thus when equations of motion are expressed in normal
coordinates, the equations are linear with constant coefficients and each con-
tains only one dependent variable.
We now calculate the energy in normal coordinates. The potential energy
arises due to the energy stored in the spring and due to the position of the
body.
V =
1
2
k(x
1
− x
2
)
2
+ mgb(1 − cos θ
1
) + mgb(1 − cos θ
2
) (8)
Now b(1 − cos θ
1
) = b
θ
2
1
2
=
x
2
1
2b
Similarly b(1 − cos θ
2
) =
x
2
2
2b
Hence V =
k
2
(x
1
− x
2
)
2
+
mgx
2
1
2b
+
mgx
2
2
2b
(9)
Kinetic energy T =
m
2
˙x
2
1
+˙x
2
2
(10)
Although there is no cross-product term in (10) for the kinetic energy, there
is one in the potential energy of the spring in (9). The presence of the cross-
product term means coupling between the components of the vibrating system.
However, in normal coordinates the cross-product terms are avoided. Using
(3) in (9) and (10)
