Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.


238 6 Oscillations
(a) Trolley moving horizontally with acceleration a
T
= T
g
g
2
+ a
2
(6.22)
(b) Trolley rolls down on a frictionless incline at an angle θ to the horizontal plane
T
= T/ cos θ (6.23)
Physical Pendulum
Any rigid body mounted such that it can swing in a vertical plane about some axis
passing through it is called a physical pendulum, Fig. 6.1.
Fig. 6.1
The body is pivoted to a horizontal frictionless axis through P and displaced from
the equilibrium position by an angle θ. In the equilibrium position the centre of mass
C lies vertically below the pivot P. If the distance from the pivot to the centre of mass
be d, the mass of the body M and the moment of inertia of the body about an axis
through the pivot I , the time period of oscillations is given by
T = 2π
1
Mgd
(6.24)
The equivalent length of simple pendulum is
L
eq
= I/Md (6.25)
The torsional oscillator consists of a flat metal disc suspended by a wire from a
clamp and attached to the centre of the disc. When displaced through a small angle
6.1 Basic Concepts and Formulae 239
about the vertical wire and released the oscillator would execute oscillations in the
horizontal plane. For small twists the restoring torque will be proportional to the
angular displacement
τ =−Cθ (6.26)
where C is known as torsional constant. The time period of oscillations is given by
T = 2π
l
C
(6.27)
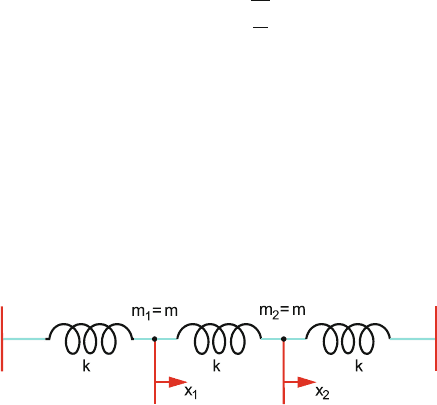
Coupled Harmonic Oscillators
Two equal masses connected by a spring and two other identical springs fixed to
rigid supports on either side, Fig. 6.2, permit the masses to jointly undergo SHM
along a straight line, so that the system corresponds to two coupled oscillators. The
equation of motion for mass m
1
is
m ¨x
1
+ k(2x
1
− x
2
) = 0 (6.28)
Fig. 6.2
and that for m
2
is
m ¨x
2
+ k(2x
2
− x
1
) = 0 (6.29)
Equations (6.28) and (6.29) are coupled equations.
Assuming x
1
= A
1
sin ωt and x
2
= A
2
sin ωt
(6.28) and (6.29) become
¨x
1
=−ω
2
A
1
sin ωt =−ω
2
x
1
(6.30)
¨x
2
=−ω
2
A
2
sin ωt =−ω
2
x
2
(6.31)
Inserting (6.30) and (6.31)in(6.28) and (6.29), we get on rearrangement
(2k −mω
2
)x
1
− kx
2
= 0 (6.32)
− kx
1
+ (2k −mω
2
)x
2
= 0 (6.33)

240 6 Oscillations
For a non-trivial solution, the determinant formed from the coefficients of x
1
and x
2
must vanish.
2k −mω
2
−k
−k 2k −mω
2
= 0
The expansion of the determinant gives a quadratic equation in ω whose solutions
are
ω
1
=
k/m (6.35)
ω
2
=
3k/m (6.36)
Normal coordinates: It is always possible to define a new set of coordinates called
normal coordinates which have a simple time dependence and correspond to the
excitation of various oscillation modes of the system. Consider a pair of coordinates
defined by
η
1
= x
1
− x
2
,η
2
= x
1
+ x
2
(6.37)
or x
1
=
1
2
(η
1
+ η
2
), x
2
=
1
2
(η
2
− η
1
) (6.38)
Substituting (6.38)in(6.28) and (6.29) we get
m( ¨η
1
+¨η
2
) + k(3η
1
+ η
2
) = 0
m( ¨η
1
−¨η
2
) + k(3η
1
− η
2
) = 0
which can be solved to yield
m ¨η
1
+ 3kη
1
= 0
m ¨η
2
+ kη
2
= 0 (6.39)
The coordinates η
1
and η
2
are now uncoupled and are therefore independent
unlike the old coordinates x
1
and x
2
which were coupled.
The solutions of (6.39)are
η
1
(t) = B
1
sin ω
1
t,η
2
(t) = B
2
sin ω
2
t (6.40)
where the frequencies are given by (6.35) and (6.36).
A deeper insight is obtained from the energies expressed in normal coordinates
as opposed to the old coordinates. The potential energy of the system
U =
1
2
kx
1
2
+
1
2
k(x
2
− x
1
)
2
+
1
2
kx
2
2
= k(x
1
2
− x
1
x
2
+ x
2
2
) (6.41)

6.1 Basic Concepts and Formulae 241
The term proportional to the cross-product x
1
x
2
is the one which expresses the cou-
pling of the system. The kinetic energy of the system is
K =
1
/
2
m ˙x
2
1
+
1
/
2
m ˙x
2
2
(6.42)
In terms of normal coordinates defined by (6.38)
U =
k
4
(η
2
1
+ 3η
2
2
) (6.43)
K =
m
4
( ˙η
2
1
+˙η
2
2
) (6.44)
Thus, the cross-product term has disappeared and the kinetic and potential energies
appear in quadratic form. Each normal coordinate corresponds to an independent
mode of vibration of the system, with its own characteristic frequency and the gen-
eral vibratory motion may be regarded as the superposition of some or all of the
independent normal vibrations.
Damped Vibrations
For small velocities the resisting force f
r
(friction) is proportional to the velocity:
f
r
=−r
dx
dt
(6.45)
where r is known as the resistance constant or damping constant. The presence of
the dissipative forces results in the loss of energy in heat motion leading to a gradual
decrease of amplitude. The equation of motion is written as
m
d
2
x
dt
2
+r
dx
dt
+ kx = 0 (6.46)
where m is the mass of the body and k is the spring constant.
Putting r/m = 2b and k/m = ω
0
2
,(6.46) becomes on dividing by m
d
2
x
dt
2
+ 2b
dx
dt
+ ω
2
0
x = 0 (6.47)
Let x = e
λt
so that dx/dt = λe
λt
and d
2
x/dt
2
= λ
2
e
λt
The corresponding characteristic equation is
λ
2
+ 2bλ +ω
0
2
= 0 (6.48)
The roots are
λ =−b ±
b
2
− ω
2
0
(6.49)

242 6 Oscillations
Calling R =
b
2
− ω
2
0
λ
1
=−b + R λ
2
=−b − R
Using the boundary conditions, at t = 0, x = x
0
and dx/dt = 0 the solution to
(6.47) is found to be
x =
1
2
x
0
e
−bt
(1 + b/R)e
Rt
+ (1 − b/R)e
−Rt
(6.50)
The physical solution depends on the degree of damping.
Case 1: Small frictional forces: b <ω
0
(underdamping)
b
2
< k/m or (r/2m)
2
< k/m
R is imaginary. R = jω
, where j =
√
−1
ω
2
= ω
2
0
− b
2
(6.51)
x = Ae
−bt
cos(ω
t + ε) (6.52)
where A = ω
0
x
0
/ω
and ε = tan
−1
(−b/ω
) (6.53)
Fig. 6.3 Underdamped
motion
Equation (6.52) represents damped harmonic motion of period
T
=
2π
ω
=
2π
ω
2
0
− b
2
(6.54)
T = 1/b is the time in which the amplitude is reduced to 1/e.
The logarithmic decrement is
= ln
A
Ae
−bT
= bT
(6.55)
Case 2: Large frictional forces (overdamping)
b >ω
0
. Distinct real roots.

6.1 Basic Concepts and Formulae 243
Both the exponential terms in (6.50) are negative and they correspond to expo-
nential decrease. The motion is not oscillatory. The general solution is of the form
x = e
−bt
(Ae
Rt
+ Be
−Rt
) (6.56)
Fig. 6.4 Overdamped motion
Case 3: Critical damping
b = ω, R = 0
Fig. 6.5 Criticallydamped
motion
The exponentials in the square bracket may be expanded to terms linear in Rt.The
solution is of the form
x = x
0
e
−bt
(1 + bt) (6.57)
The motion is not oscillatory and is said to be critically damped. It is a transition
case and the motion is just aperiodic or non-oscillatory. There is an initial rise in
the displacement due to the factor (1 + bt) but subsequently the exponential term
dominates.
Energy and Amplitude of a Damped Oscillator
E(t) = E
0
e
−t/t
c
(6.58)
244 6 Oscillations
where t
c
= m/r
A(t) = A
0
e
−t/2t
c
(6.59)
Quality factor
Q = ωt
c
= ωm/r (6.60)
ω
= ω
0
1 −
1
4Q
2
(6.61)
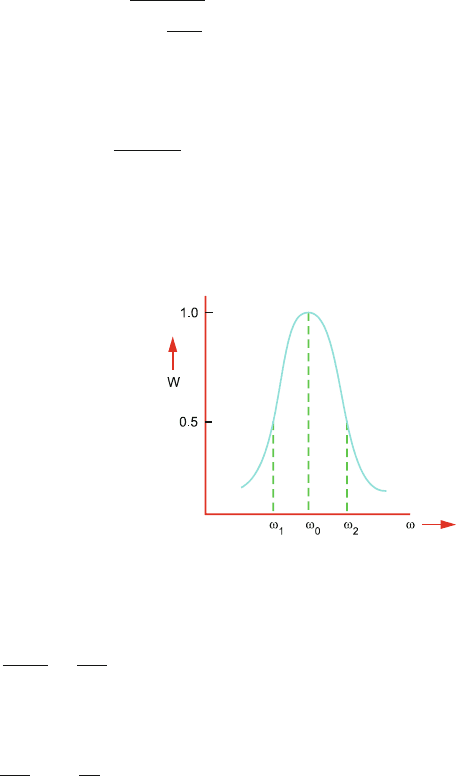
The value of quality factor indicates the sharpness of resonance.
Q =
ω
0
ω
2
− ω
1
(6.62)
where ω
0
is the resonance angular frequency and ω
2
and ω
1
are, respectively, the
two angular frequencies above and below resonance at which the average power has
dropped to one-half its resonance value. (Fig. 6.6).
Fig. 6.6 Resonance
frequency curve, ω
0
is the
resonance angular frequency.
ω
1
and ω
2
are defined in the
text
Forced vibrations are set up by a periodic force F cos ωt.
Equation of motion of a particle of mass m
md
2
x
dt
2
+
rdx
dt
+ kx = F cos ωt (6.63)
or
d
2
x
dt
2
+ 2b
dx
dt
+ ω
2
0
x = p cos ωt (6.64)
where
k/m = ω
2
0
, r/m = 2b and F/m = p (6.65)

6.2 Problems 245
ω
0
being the resonance frequency.
x = A cos(ωt −ε) (6.66)
tan ε =
2bω
ω
2
0
− ω
2
(6.67)
Mechanical impedance
Z
m
=
(ω
2
0
− ω
2
)
2
+ 4b
2
ω
2
(6.68)
A =
p
Z
m
(6.69)
Q =
ω
0
2b
(6.70)
Power
W =
F
2
− sin ε
2Z
m
(6.71)
6.2 Problems
6.2.1 Simple Harmonic Motion (SHM)
6.1 The total energy of a particle executing SHM of period 2π sis0.256J.The
displacement of the particle at π/4s is 8
√
2 cm. Calculate the amplitude of
motion and mass of the particle.
6.2 A particle makes SHM along a straight line and its velocity when passing
through points 3 and 4 cm from the centre of its path is 16 and 12 cm/s, respec-
tively. Find (a) the amplitude; (b) the time period of motion.
[Northern Universities of UK]
6.3 A small bob of mass 50 g oscillates as a simple pendulum, with amplitude 5 cm
and period 2 s. Find the velocity of the bob and the tension in the supporting
thread when velocity of the bob is maximum.
[University of Aberystwyth, Wales]

246 6 Oscillations
6.4 A particle performs SHM with a period of 16 s. At time t = 2 s, the particle
passes through the origin while at t = 4 s, its velocity is 4 m/s. Show that the
amplitude of the motion is 32
√
2/π.
[University of Dublin]
6.5 Show that given a small vertical displacement from its equilibrium position
a floating body subsequently performs simple harmonic motion of period
2π
√
V/Ag where V is the volume of displaced liquid and A is the area of
the plane of floatation. Ignore the viscous forces.
6.6 Imagine a tunnel bored along the diameter of the earth assumed to have constant
density. A box is thrown into the tunnel (chute). (a) Show that the box executes
SHM inside the tunnel about the centre of the earth. (b) Find the time period of
oscillations.
6.7 A particle which executes SHM along a straight line has its motion represented
by x = 4sin(πt/3 + π/6).Find(a) the amplitude; (b) time period; (c) fre-
quency; (d) phase difference; (e) velocity; (f) acceleration, at t = 1s, x being
in cm.
6.8
(a) At what distance from the equilibrium position is the kinetic energy equal
to the potential energy for a SHM?
(b) In SHM if the displacement is one-half of the amplitude show that the
kinetic energy and potential energy are in the ratio 3:1.
6.9 AmassM attached to a spring oscillates with a period 2 s. If the mass is
increased by 2 kg, the period increases by 1 s. Assuming that Hooke’s law is
obeyed, find the initial mass M.
6.10 A particle vibrates with SHM along a straight line, its greatest acceleration is
5π
2
cm/s
2
, and when its distance from the equilibrium is 4 cm the velocity of
the particle is 3π cm/s. Find the amplitude and the period of oscillation of the
particle.
6.11 If the maximum acceleration of a SHM is α and the maximum velocity is
β, show that the amplitude of vibration is given by β
2
/α and the period of
oscillation by 2πβ/α.
6.12 If the tension along the string of a simple pendulum at the lowest position is
1% higher than the weight of the bob, show that the angular amplitude of the
pendulum is 0.1 rad.
6.13 A particle executes SHM and is located at x = a, b and c at time t
0
,2t
0
and
3t
0
, respectively. Show that the frequency of oscillation is
1
2πt
0
cos
−1
a + c
2b
.
6.14 A 4 kg mass at the end of a spring moves with SHM on a horizontal frictionless
table with period 2 s and amplitude 2 m. Determine (a) the spring constant;
(b) maximum force exerted on the spring.
6.2 Problems 247
6.15 A particle moves in the xy-plane according to the equations x = a sin ωt;
y = b cos ωt. Determine the path of the particle.
6.16 (a) Prove that the force F =−kx
´
i acting in a SHO is conservative. (b) Find
the potential energy of an SHO.
6.17 A 2 kg weight placed on a vertical spring stretches it 5 cm. The weight is
pulled down a distance of 10 cm and released. Find (a) the spring constant;
(b) the amplitude; (c) the frequency of oscillations.
6.18 Amassm is dropped from a height h on to a scale-pan of negligible weight,
suspended from a spring of spring constant k. The collision may be considered
to be completely inelastic in that the mass sticks to the pan and the pan begins
to oscillate. Find the amplitude of the pan’s oscillations.
6.19 A particle executes SHM along the x-axis according to the law x = A sin ωt.
Find the probability dp(x) of finding the particle between x and x +dx.
6.20 Using the probability density distribution for the SHO, calculate the mean
potential energy and the mean kinetic energy over an oscillation.
6.21 A cylinder of mass m is allowed to roll on a smooth horizontal table with a
spring of spring constant k attached to it so that it executes SHM about the
equilibrium position. Find the time period of oscillations.
6.22 Two simple pendulums of length 60 and 63 cm, respectively, hang vertically
one in front of the other. If they are set in motion simultaneously, find the time
taken for one to gain a complete oscillation on the other.
[Northern Universities of UK]
6.23 A pendulum that beats seconds and gives correct time on ground at a certain
place is moved to the top of a tower 320 m high. How much time will the
pendulum lose in 1 day? Assume earth’s radius to be 6400 km.
6.24 Taking the earth’s radius as 6400 km and assuming that the value of g inside
the earth is proportional to the distance from the earth’s centre, at what depth
below the earth’s surface would a pendulum which beats seconds at the earth’s
surface lose 5 min in a day?
[University of London]
6.25
A U-tube is filled with a liquid, the total length of the liquid column being
h. If the liquid on one side is slightly depressed by blowing gently down, the
levels of the liquid will oscillate about the equilibrium position before finally
coming to rest. (a) Show that the oscillations are SHM. (b) Find the period of
oscillations.
6.26 A gas of mass m is enclosed in a cylinder of cross-section A by means of a
frictionless piston. The gas occupies a length l in the equilibrium position and
is at pressure P. (a) If the piston is slightly depressed, show that it will execute
SHM. (b) Find the period of oscillations (assume isothermal conditions).
