Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.


5.3 Solutions 217
Fig. 5.16
At the apogee (farthest point), the velocity of the satellite is perpendic-
ular to the radius vector. Therefore, the angular momentum at the apogee
= (mv)(5R/2).
Conservation of angular momentum gives
5
2
mv R =
m
2
v
0
R
or v =
v
0
5
(1)
The kinetic energy at the surface K
0
=
1
2
mv
2
0
and potential energy U
0
=
−
GMm
R
.
Therefore, the total mechanical energy at the surface is
E
0
=
1
2
mv
2
0
−
GMm
R
(2)
At the apogee kinetic energy K =
1
2
mv
2
and the potential energy U =
−
2GMm
5R
.
Therefore, the total mechanical energy at the apogee is
E =
1
2
mv
2
−
2
5
GMm
R
(3)
Conservation of total energy requires that E = E
0
. Eliminating v in (3) with
the aid of (1) and simplifying we get
v
0
=
5GM
4R
218 5 Gravitation
5.31 For an elliptic orbit
v =
GM
2
r
−
1
a
∴ v
max
=
GM
2
r
min
−
1
a
=
GM(2a −r
min
)
ar
min
=
GMr
max
ar
min
(1)
as r
max
+r
min
= 2a
v
min
=
GM
2
r
max
−
1
a
=
GM(2a −r
max
)
ar
max
=
GMr
min
ar
max
(2)
Multiplying (1) and (2)
v
max
v
min
=
GM
a
or
√
v
max
v
min
=
GM
a
= a
GM
a
3
=
2πa
T
as T = 2π
a
3
GM
∴ a =
T
2π
√
v
max
v
min
5.32
T = 2π
r
3
GM
(1)
But r = a + b + c (2)
Combining (1) and (2)
M =
4π
2
(a + b + c)
3
GT
2
5.33 L =|r × p|=rp sin θ
L per unit mass = rv sin θ
= (1.75 ×1.5 × 10
11
)(3 × 10
4
) sin 30
◦
= 3.9375 ×10
15
m
2
/s
When the comet is closest to the sun its velocity will be perpendicular to
the radius vector. The angular momentum L
= r
v
. Angular momentum
conservation requires
5.3 Solutions 219
L
= L
∴ v
=
L
r
=
L
r
=
3.9375 × 10
15
0.39 × 1.5 × 10
11
= 6.73 ×10
4
m/s = 67.3km/s
Total energy per unit mass
E =
1
2
v
2
−
GM
r
=
1
2
(3×10
4
)
2
−
6.67 × 10
−11
× 2 × 10
30
1.75 × 10
11
=−3.12×10
8
J
a negative quantity. Therefore the orbit is bound.
5.34
(a) The centripetal force is provided by the gravitational force.
GM
E
M
S
R
2
=
M
E
v
2
R
or GM
S
= v
2
R (1)
(b) Total energy of the comet when it is closest to the sun
E =
1
2
M
C
(2v)
2
−
GM
C
M
S
R/2
(2)
Using (1) in (2) we find E = 0.
(c) At the distance of the closest approach, the comet’s velocity is perpendic-
ular to the radius vector. Therefore the angular momentum
L = M
C
(2v)
R
2
= M
C
v R (3)
Let v
t
be the comet’s velocity which is tangential to the earth’s orbit at P.
Then the angular momentum at P will be
L
= M
c
v
t
R (4)
Angular momentum conservation gives
M
C
v
t
R = M
C
v R (5)
or v
t
= v (6)
(d) The total energy of the comet at P is
E
=
1
2
M
C
(v
)
2
−
GM
S
M
C
R
= 0(7)
where v
is the comet’s velocity at P, because E
= E = 0, by energy
conservation.

220 5 Gravitation
Using (1) in (7) we find
v
=
√
2v (8)
If θ is the angle between v
and the radius vector R angular momentum
conservation gives
M
C
v R = M
C
v
R sin θ = M
C
√
2v R sin θ
or sin θ =
1
√
2
θ = 45
◦
5.35 At both perigee and apogee the velocity of the satellite is perpendicular to the
radius vector. In order to show that the angular momentum is conserved we
must show that
mv
p
r
p
= mv
A
r
A
or v
p
r
p
= v
A
r
A
where m is the mass of the satellite.
v
p
r
p
= 10.25 ×6570 = 67342.5
v
A
r
A
= 1.594 ×42250 = 67346.5
The data are therefore consistent with the conservation of angular momentum.
5.36
(a)
v
0
=
GM
2
r
−
1
a
(1)
GM = (6.67 × 10
−11
)(6 × 10
24
) = 4 × 10
14
r = R = 6.4 × 10
6
a = 8 × 10
7
m
v
0
= 1.095 ×10
4
m/s = 10.095 km/s
(b)
ε =
1 +
2EJ
2
G
2
M
2
m
3
(2)
J = mRv
0
sin 45
◦
=
mRv
0
√
2
(3)
E =−
GMm
2a
(4)
Combining (1), (2), (3) and (4)
5.3 Solutions 221
ε =
1 −
R
a
+
1
2
R
2
a
2
(5)
Now
R
a
=
6400
80000
= 0.08
∴ ε = 0.96
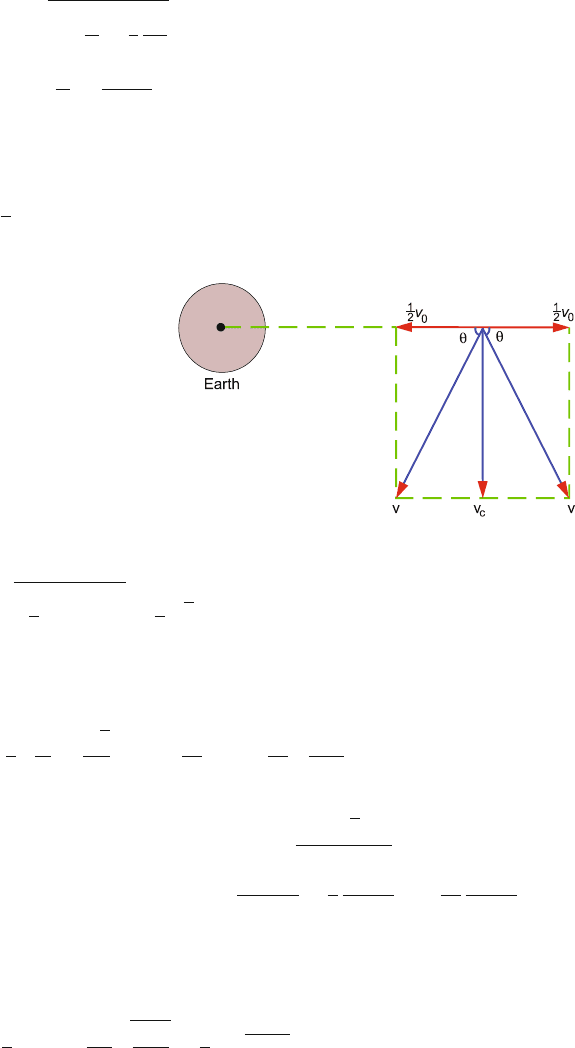
5.37 The resultant velocity v of each fragment is obtained by combining the veloc-
ities
1
2
v
0
and v
0
vectorially, Fig. 5.17.
Fig. 5.17
v =
1
2
v
0
2
+ v
2
0
=
1
2
√
5v
0
Kinetic energy of each fragment
K =
1
2
m
2
√
5
2
v
0
2
=
5
16
mv
2
0
=
5
16
m
GM
r
Potential energy of each fragment U =−
GM
1
2
m
r
∴ Total energy E = K +U =
5GMm
16r
−
1
2
GMm
r
=−
3
16
GMm
r
If v makes on angle θ with the radius vector r, then v sin θ = v
0
. The angular
momentum of either fragment about the centre of the earth is
J =
1
2
mv
0
r =
mr
2
GM
r
=
1
2
m
√
GMr
222 5 Gravitation
5.38 Velocity at the nearer apse is given by
v
2
= GM
2
a(1 − ε)
−
1
a
=
GM
a
1 + ε
1 − ε
(1)
as there is no instantaneous change of velocity. If a
1
is the semi-major axis for
the new orbit
v
2
= GM
2
a(1 − ε)
−
1
a
1
(2)
As the nearer and farther apses are inter-changed
a
1
(1 − ε
1
) = a(1 + ε) (3)
Equating the right-hand side of (1) and (2) and eliminating a
1
from (3) and
solving for ε
1
we get
ε
1
=
ε(3 + ε)
1 − ε
5.39
(a)
1
T
dt
r
=
1
T
d θ
r
˙
θ
(1)
Now, J = mr
2
˙
θ(constant) (2)
∴
1
T
dt
r
=
m
TJ
r d θ (3)
r =
a(1 − ε
2
)
1 + ε cos θ
(4)
Using (4) in (3)
1
T
dt
r
=
ma(1 −ε
2
)
TJ
2π
0
d θ
1 + ε cos θ
=
ma(1 −ε
2
)
TJ
2π
√
1 − ε
2
(5)
where we have used the integral
2π
0
d θ
a + b cos θ
=
2π
√
a
2
− b
2
Further T =
2πma
2
√
1 − ε
2
J
(6)
Using (6) in (5)
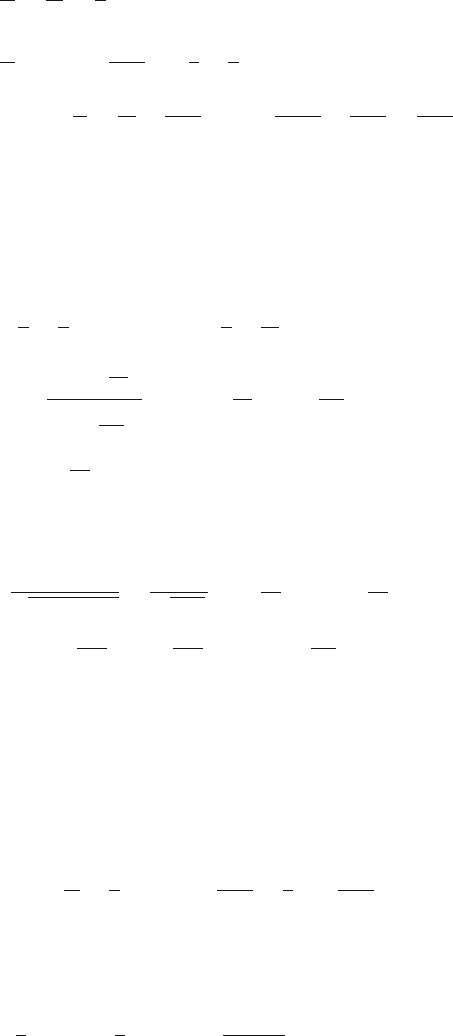
5.3 Solutions 223
1
T
dt
r
=
1
a
(7)
(b)
1
T
v
2
dt =
GM
T
2
r
−
1
a
dt
= 2GM
1
T
dt
r
−
GM
Ta
dt =
2GM
a
−
GM
a
=
GM
a
where we have used (7) and put
dt = T .
5.40 The distance between the focus and the end of minor axis is a.Letthenew
semi-major axis be a
1
. Since the instantaneous velocity does not change
GM
2
a
−
1
a
= G(M +m)
2
a
−
1
a
1
or a
1
=
a
1 +
m
M
1 +
2m
M
≈ a
1 +
m
M
1 −
2m
M
a
1
= a
1 −
m
M
(1)
The new time period
T
1
=
2πa
3/2
1
√
G(M +m)
=
2πa
3/2
√
GM
1 −
m
M
3/2
1 +
m
M
−1/2
≈ T
1 −
3m
2M
1 −
m
2M
≈ T
1 −
2m
M
where we have used binomial expansion and the value of the old time period.
5.41 Case 1: Apse is farther
It is sufficient to show that the total energy is zero.
r
1
= a(1 + ε) = a(1 + 0.5) = 1.5a
v
2
1
= GM
2
r
1
−
1
a
= GM
2
1.5a
−
1
a
=
GM
3a
New velocity v
1
= 2v
1
.
New kinetic energy
K
1
=
1
2
m(v
1
)
2
=
1
2
m(2v
1
)
2
=
2GMm
3a

224 5 Gravitation
The potential energy is unaltered and is therefore
U
1
=−
GMm
r
1
=−
2GMm
3a
Total energy E
1
= K
+U
1
=
2GMm
3a
−
2GMm
3a
= 0
Case 2: Apse is nearer
It is sufficient to show that the total energy is positive.
r
2
= a(1 − ε) = a(1 − 0.5) = 0.5a
v
2
2
= GM
2
r
2
−
1
a
= GM
2
0.5a
−
1
a
=
3GM
a
New velocity v
2
= 2v
2
.
New kinetic energy K
2
=
1
2
m
v
2
2
=
1
2
m(2v
2
)
2
=
6GMm
a
Potential energy is unaltered and is given by
U
2
=−
GMm
r
2
=−
GMm
0.5a
=−
2GMm
a
Total energy E
2
= K
2
+U
2
=
6GMm
a
−
2GMm
a
=+
4GMm
a
,
which is a positive quantity.
5.42 The velocity of the particle in the orbit is given by
v
2
= GM
2
r
−
1
a
When the particle is at one extremity of the minor axis, r = a
v
2
= GM
2
a
−
1
a
=
GM
a
Let the new axes be 2a
1
and 2b
1
. By problem the force is increased by half,
but the velocity at r = a is unaltered.
v
2
= 1.5 GM
2
a
−
1
a
1
=
GM
a
∴ 2a
1
=
3a
2

5.3 Solutions 225
As v is unaltered in both magnitude and direction, the semi-latus rectum l =
b
2
a
= a(1 − ε
2
). The constant h
2
= (GM) (semi-latus rectum) is unchanged.
∴ GM
b
2
a
=
3
2
GM
b
2
1
a
1
∴ b
2
1
=
2b
2
3
a
1
a
=
2
3
·
3
4
b
2
∴ 2b
1
=
√
2b
5.43
(a) The forces acting on the satellite are gravitational force and centripetal
force.
(b) Equating the centripetal force and gravitational force
mv
2
R
= mg
∴ v =
gR =
2π R
T
∴ T = 2π
R
g
= 2π
R
3
GM
(1)
(c) The geocentric satellite must fly in the equatorial plane so that its cen-
tripetal force is entirely used up by the gravitational force. Second, it must
fly at the right altitude so that its time period is equal to that of the diurnal
rotation of the earth.
(d) 24 h.
(e) Using (1)
r =
T
2
GM
4π
2
1/3
Using T = 86, 400 s, G = 6.67×10
−11
kg
−1
m
3
/s
2
, M = 6.4 ×10
24
kg,
we find r = 4.23 × 10
7
m or 42,300 km.
5.44 At both perigee and apogee v is perpendicular to r. Angular momentum con-
servation gives mv
A
r
A
= mv
p
r
p
r
A
= 2a −r
p
= 4r −r = 3r
v
A
=
vr
3r
=
v
3
5.45 The orbit of the small body will be a hyperbola with the heavy body at the
focus F,Fig.5.18.

226 5 Gravitation
Fig. 5.18
r =
a(ε
2
− 1)
ε cos θ − 1
(1)
As r →∞, the denominator on the right-hand side of (1) becomes zero and
the limiting angle θ
0
is given by
cos θ
0
=
1
ε
or cot θ
0
=
1
√
ε
2
− 1
The complete angle of deviation
φ = π − 2θ
0
or
φ
2
=
π
2
− θ
0
tan
φ
2
= cot θ
0
=
1
√
ε
2
− 1
But ε =
1 +
2Eh
2
G
2
M
2
where h = pv and E =
1
2
v
2
∴ tan
φ
2
=
1
√
ε
2
− 1
=
GM
h
√
2E
=
GM
pv
2
5.46 In Fig. 5.19
r =
2a
1 + cos θ
r
2
˙
θ = h (constant, law of areas)
