Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book

Подождите немного. Документ загружается.

4.3 Solutions 187

Integrating (11)

˙z



=−gt (12)

and z



=−

(13)

with the initial condition that at t = 0, ˙z



= 0, z



= 0.

Using (12) in (10) and integrating twice

˙y



= ω gt

cos λ (14)

because ( ˙y



)

= 0.



ω gt

cos λ (15)

because (y



)

= 0.

Setting −z



= h =

(

1/2

)

,ort =

√

2h/g, in (15) the body undergoes

eastward deviation through a distance

d = y



ω cos λ



(16)

4.68

coriolis

=−2mω × v

cor

= 2mωv

sin θ = 2 × 5 × 10

× 7.27 × 10

−5

8000

86, 400

(∵ θ = 90

◦

)

= 6730 N due north

4.69 Coriolis action on a mass m of water towards the eastern side (Fig. 4.35)is

m ¨y



= 2mvω sin λ (1)

Fig. 4.35

West

188 4 Rotational Dynamics

Let N be the normal reaction and let the water level be tilted through an angle

θ. Resolve N into horizontal and vertical components and balance them with

the Coriolis force and the weight, respectively.

N sin θ = 2m vω sin λ

N cos θ = mg

Dividing the equations, tan θ =

= 2 vωsin λ

or d =

2bvω

sin λ

4.70 By eqn. (15) prob. (4.67)



ωgt

cos λ (1)



(2)

Eliminate t between (1) and (2) to ﬁnd

2

3

cos

or y

2

= Cz

3

(semi-cubical parabola)

where C = constant.

4.71

cor

= 2m vω sin λ

= 2 ×10

× 15 × 7.27 × 10

−5

sin 60

◦

= 1889 N on the right rail.

4.72 The difference between the lateral forces on the rails arises because when

the train reverses its direction of motion Coriolis force also changes its sign,

the magnitude remaining the same. Therefore, the difference between the lat-

eral force on the rails will be equal to 2m vω cos λ − (−2m vω cos λ) or

4mvω cos λ.

4.73 The displacement from the vertical is given by



− ut



ω cos λ



× 9.8 × 10

− 100 × 10



× 7.27 × 10

−5

cos 60

◦

=−0.245 m =−24.5cm

Thus the body has a displacement of 24.5 cm on the west.

Chapter 5

Gravitation

Abstract Chapter 5 involves problems on gravitational ﬁeld and potential for

various situations variation of g, rocket motion, orbital motion of planets, satellites

and meteorites, circular and elliptic motion, bound and unbound orbits, Kepler’s

laws, equation of motion under various types of forces.

5.1 Basic Concepts and Formulae

F =−Gm

(gravitational force) (5.1)

The negative sign shows that the force is attractive.

When SI units are used the gravitational constant

G = 6.67 ×10

−11

−1

−2

The intensity or ﬁeld strength g of a gravitational ﬁeld is equal to the force exerted

on a unit mass placed at that point.

g =−Gm/r

(5.2)

The (negative) gravitational potential at a given point, due to any system of

masses, is the work done in bringing a unit mass from inﬁnity up to that point.

The zero potential is chosen conventionally at inﬁnity. Symbolically

g =−

∂V

∂r

(5.3)

V =−Gm/r (5.4)

The potential energy

U =−GMm/r (5.5)

189

190 5 Gravitation

Spherical Shell

The gravitational intensity due to a spherical shell of radius a.

g(r) = 0 (r < a)

=−GM/r

(r > a) (5.6)

where r is measured from the centre of the shell. The potential

V (r) =−GM/a (r < a)

=−GM/r (r > a) (5.7)

Uniform Solid Sphere

g(r) =−GMr/a (r ≤ a)

=−GM/r

(r ≥ a) (5.8a)

V (r) =−



3 −



(r ≤ a)

=−GM/r (r ≥ a) (5.8b)

Potential energy of a uniform sphere

U =−3GM

/5a (5.9)

Variation of g on Earth

(a)

Altitude: g = g

/(1 + h/R)

(5.10)

g = g



1 −



(h << R)(5.10a)

(b) Latitude ( λ) (at sea level)

= 9.83215 −0.05178 cos

λ (5.11)

Formula (5.11) is accurate to better than two parts in a million.



= g − Rω

cos

λ (5.12)

where ω = 7.27 ×10

−5

/s and R = 6.4 × 10

(d) Depth (d) (constant density model)

g = g

(1 − d/R) (5.13)

5.1 Basic Concepts and Formulae 191

Relation Between g and G

g = GM/r

where M is the mass of parent body and r ≥ R.

Kepler’s Laws

(i) All planets move in an elliptic path, with the sun at one focus. This is a conse-

quence of inverse square law of gravitation and the constancy of total energy

and angular momentum.

(ii) A line drawn from the sun to the planet sweeps out equal areas in equal times.

This is a consequence of the constancy of angular momentum.

(iii) The squares of the period of rotation of planets about the sun are proportional

to the cubes of the semi-major axes of the ellipses. This is a consequence of

the inverse square law of gravitation for circular orbits.

Central force is a conservative force which acts along a line connecting the cen-

tres of particles.

If F is a central force then curl F = 0.

Areal velocity (C) and the angular momentum (J):

J = 2mC (5.14)

where m is the mass of the orbiting body.

Orbits of Planets and Satellites

Circular orbits:

Orbital velocity v



GM/r =

√

gr (5.15)

Escape velocity v

√



2GM/R =



R (5.16)

Time period

T = 2π



/GM (5.17)

If the planet’s mass cannot be ignored in comparison with the sun’s mass then

(5.17) is modiﬁed as

T = 2π



/G(M +m) (5.18)

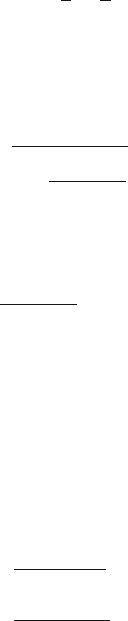
192 5 Gravitation

Total energy:

E =−GMm/2r (5.19)

Elliptic Orbits

Orbital velocity

= GM



−



(5.20)

where r is the distance of the planet/satellite from the centre of parent body and a is

the semi-major axis.

The eccentricity

ε =



1 +

2EJ

(5.21)

Total energy

E =−

(1 − ε

) (5.22)

E =−GMm/2a (5.23)

When the orbiting body is at the maximum distance from the parent body then

r = r

max

is called aphelion and the minimum distance r = r

min

is called perihe-

lion for the planetary motion. For the satellites the corresponding terms are apogee

and perigee. At both perigee (perihelion) and apogee (aphelion) the velocity of the

orbiting body is perpendicular to the radius vector and they constitute the turning

points.

ε =

max

−r

min

max

min

(5.24)

ε =

max

− v

min

max

+ v

min

(5.25)

Classiﬁcation of Orbits

Circle: ε = 0 E < 0

Ellipse: 0 <ε<1 E < 0

Parabola: ε = 1 E = 0

Hyperbola: ε>1 E > 0

To determine the law of force, given the orbit by (r, θ) equation. Let f represent

force per unit mass. Using the formula

5.2 Problems 193



d θ



(5.26)

f =−

(5.27)

where p is the impact parameter and h is the angular momentum per unit mass.

5.2 Problems

5.2.1 Field and Potential

5.1 Calculate the gravitational force between two lead spheres of radius 10 cm in

contact with one another, G = 6.67 × 10

−11

MKS units. Density of lead =

11,300 kg/m

[University of Dublin]

5.2 Considering Fig. 5.1, what is the magnitude of the net gravitational force

exerted on the uniform sphere, of mass 0.010 kg, at point P by the other two

uniform spheres, each of mass 0.260 kg, that are ﬁxed at points A and B as

shown.

[The University of Wales, Aberystwyth 2005]

Fig. 5.1

5.3 Two bodies of mass m and M are i nitially at rest in an inertial reference frame at

a great distance apart. They start moving towards each other under gravitational

attraction. Show that as they approach a distance d apart (d << r), their rela-

tive velocity of approach will be



2G(M + m)

, where G is the gravitational

constant.

194 5 Gravitation

5.4 If the earth suddenly stopped in its orbit assumed to be circular, ﬁnd the time

that would elapse before it falls into the sun.

5.5 Because of the rotation of the earth a plumb bob when hung may not point

exactly in the direction of the earth’s gravitational force on the plumb bob. It

may slightly deviate through a small angle.

(a) Show that at latitude λ, the deﬂection angle θ in radians is given by

θ =



2π



sin 2λ

where R is the radius of earth and T is the period of the earth’s rotation.

(b) At what latitude is the deﬂection maximum?

5.6 Show that the gravitational energy of earth assumed to be the uniform sphere

of radius R and mass M is 3GM

/5R. What is the potential energy of earth

assuming it to be a uniform sphere of radius R = 6.4 × 10

m and of mass

M = 6.0 × 10

kg.

5.7 Assuming that the earth has constant density, at what distance d from the earth’s

surface the gravity above the earth is equal to that below the surface.

5.8 Assuming the radius of the earth to be 6.38×10

cm, the gravitational constant

to be 6.67 ×10

−8

g/m/s

, acceleration due to gravity on the surface to be

980 cm/s

, ﬁnd the mean density of the earth.

[University of Cambridge]

5.9 How far from the earth must a body be along a line towards the sun so that the

sun’s gravitational pull balances the earth? The sun is about 9.3 ×10

km away

and its mass is 3.24 × 10

, where M

is the mass of the earth.

5.10 Assuming the earth to be a perfect sphere of r adius 6.4 × 10

cm, ﬁnd the

difference due to the rotation of the earth in the value of g at the poles and at

the equator.

[Northern Universities of UK]

5.11 Derive an expression for the gravitational potential V (r) due to a uniform

solid sphere of mass M and radius R when r < R.

5.12 Derive an expression for the potential due to a thin uniform rod of mass M

and length L at a point distant d from the centre of the rod on the axial line of

the rod.

5.13 Show that for a satellite moving close to the earth’s surface along the equator,

moving in the western direction will require launching speed 11% higher than

that moving in the eastern direction.

5.2 Problems 195

5.14 A thin wire of linear mass density λ is bent in the form of a quarter circle of

radius R (Fig. 5.2). Calculate the gravitational intensity at the centre O.

Fig. 5.2

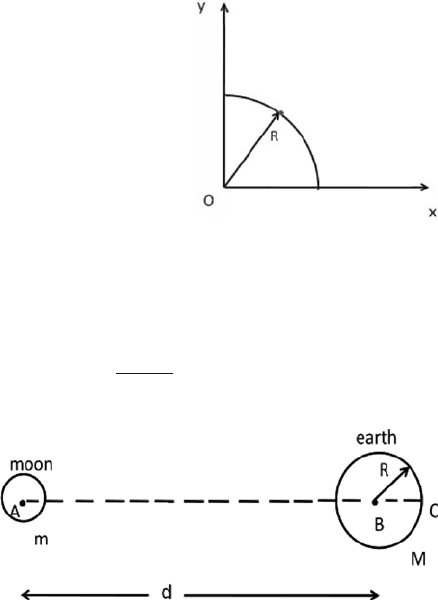
5.15 A tidal force is exerted on the ocean by the moon. This is estimated by the

differential (g) which is the difference of the acceleration at B and that at C

due to the moon (Fig. 5.3). If R is the radius of the earth, d the distance of

separation of the centre of earth and moon, M and m the mass of the earth and

moon, respectively, show that g ≈

2GmR

Fig. 5.3

5.16 Assume that a star has uniform density. Show that the gravitational pressure

P ∝ V

−4/3

, where V is the volume.

5.17 Find the gravitational ﬁeld due to an inﬁnite line mass of linear density λ,at

distance R.

5.18 If the earth–moon distance is d and the mass of earth is 81 times that of the

moon, locate the neutral point on the line joining the centres of the earth and

moon.

5.19 A particle of mass m was taken from the centre of the base of a uniform

hemisphere of mass M and radius R to inﬁnity. Calculate the work done in

overcoming gravitational force due to the hemisphere.

5.20 The cross-section of a spherical shell of uniform density and mass M and of

radii a and b is shown in Fig. 5.4. How does the gravitational ﬁeld vary in the

region a < r < b?

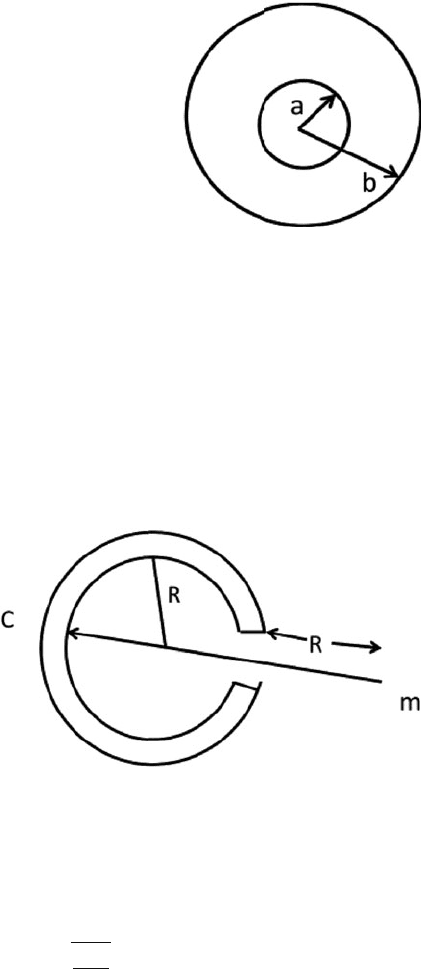
196 5 Gravitation

Fig. 5.4

5.21 Find the variation of the magnitude of gravitational ﬁeld along the z-axis due

toadiscofradius‘a’ and surface density σ , lying in the xy-plane.

5.22 Figure 5.5 shows a spherical shell of mass M and radius R in a force-free

region with an opening. A particle of mass m is released from a distance R in

front of the opening. Calculate the speed with which the particle will hit the

point C on the shell, opposite to the opening.

Fig. 5.5

5.2.2 Rockets and Satellites

5.23 A particle of mass m is ﬁred upwards from the surface of a planet of mass M

and radius R with velocity v =



. Show that the maximum height which

the particle attains is R/3.

5.24 Consider a nebula in the form of a ring of radius R and mass M. A star of

mass m(m << M) is located at distance r from the centre of the r ing on its