Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.

4.3 Solutions 167
The first term in square brackets is the M.I. of the bar, the second and the
third terms are for the M.I. of the particles which stick to the bar.
Thus ω =
v
5a
(d) E =
1
2
Iω
2
=
1
2
30 ma
2
v
5a
2
=
3
5
mv
2
4.33 Let the potential energy be zero when the rod is in the horizontal position. In
the vertical position the loss in potential energy of the system will be mg(d +
2d) = 3mgd . The gain in rotational kinetic energy will be
1
2
Iω
2
=
1
2
(I
1
+ I
2
)ω
2
=
1
2
md
2
+ m(2d)
2
ω
2
=
5
2
md
2
ω
2
Gain in kinetic energy = loss of potential energy
5
2
md
2
ω
2
= 3mgd
∴ ω =
6g
5α
The linear velocity of the lower mass in the vertical position will be
v = (ω)(2d) =
24
5
gd
4.34 Conservation of J gives
I
1
ω
1
= I
2
ω
2
2
5
MR
2
2π
T
1
=
2
5
M
R
2
2
2π
T
2
∴ T
2
=
T
1
4
=
24
4
= 6h
4.35 The moment of inertia of the pole of length L and mass M about O is
(Fig. 4.26)
I =
ML
2
3
(1)
The torque τ = Iα = Mgx (2)
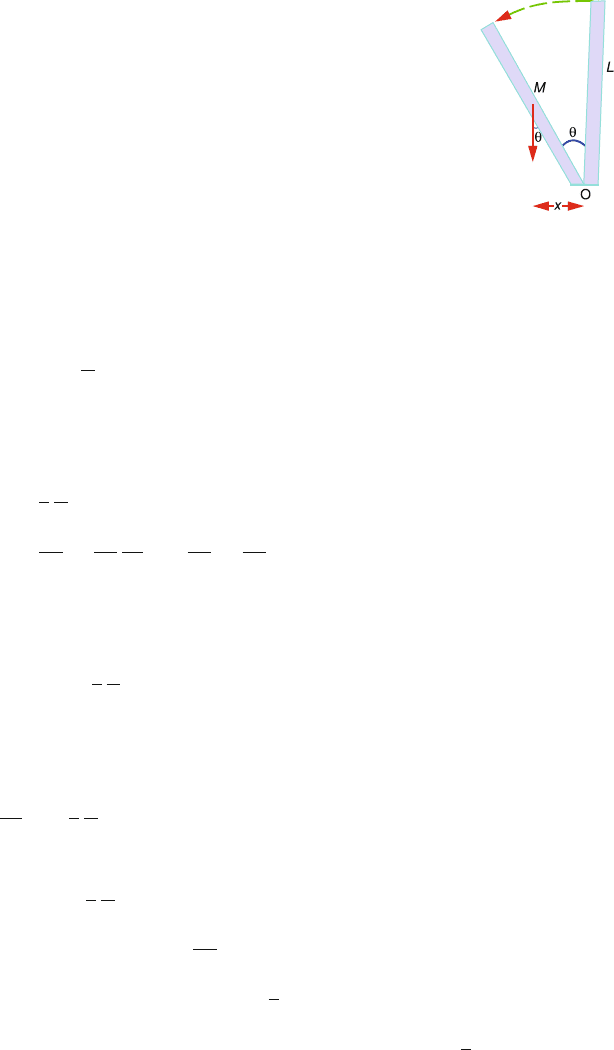
168 4 Rotational Dynamics
Fig. 4.26
where x is the projection of the centre of mass on the ground from the point
O and α is the angular acceleration.
Now x =
L
2
sin θ (3)
Using (1) and (3) in (2)
α =
3
2
g
L
sin θ (4)
α =
dω
dt
=
dω
dθ
dθ
dt
= ω
dω
dθ
=
3g
2L
sin θ
Integrating
ω dω =
3
2
g
L
sin θ dθ +C
where C = constant.
ω
2
2
=−
3
2
g
L
cos θ + C (5)
When θ = 0,ω= 0
∴ C =
3
2
g
L
(6)
Using (6) in (5) ω
2
=
3g
2L
(1 − cos θ)
Radial acceleration a
R
= ω
2
L =
3
2
g(1 − cos θ)
Tangential acceleration of the top of the pole a
T
= α L =
3
2
g sin θ

4.3 Solutions 169
4.36
J = at
2
ˆ
i
+ b
ˆ
j
(1)
∴ τ =
dJ
dt
= 2at
ˆ
i (2)
Take the scalar product of J and τ .
J · τ = 2a
2
t
3
=
a
2
t
4
+ b
2
(2at ) cos 45
◦
Simplify and solve for t. We get
t =
b
a
(3)
Using (3) in (2),
|
τ
|
= 2
√
ab
Using (3) in (1),
|
J
|
=
√
2b
4.37 Consider a ring of r adii r and r +dr, concentric with the disc (r < R).Ifthe
surface density is σ , the mass of the ring is dm = 2πrdrσ . The moment of
inertia of the ring about the central axis will be
dI = (2πr drσ)r
2
= 2πσr
3
dr (1)
and the corresponding torque will be
dτ = αdI = 2πσαr
3
dr (2)
The frictional force on the ring is μdmg= μ(2πr drσ)g and the correspond-
ing torque will be
dτ = μ(2πr drσ)gr = 2πσμgr
2
dr (3)
Calculating the torques from (2) and (3) for the whole disc and equating them
R
0
2πσαr
3
dr =
R
0
2πσμgr
2
dr
∴ α =
4μg
3R
(4)
but 0 = ω − αt
∴ t =
ω
α
=
3ωR
4μg
170 4 Rotational Dynamics
4.38 The horizontal component of force at Q is mv
2
/R. The drop in height in com-
ingdowntoQis
(6R − R) = 5R
Gain in kinetic energy = loss in potential energy
7
10
mv
2
= (mg)(5R)
∴
mv
2
R
=
50
7
mg
4.39 Let the velocity on the top be v. Energy conservation gives
1
2
mv
2
0
= mgr cos θ
0
+
1
2
mv
2
(1)
where r cos θ
0
is the height to which the particle is raised. Angular momentum
conservation gives
mvr = mv
0
r sin θ
0
(2)
Eliminating v between (1) and (2) and simplifying
v
0
=
2gr
cos θ
0
4.40 Equation of motion is
ma = mg sin θ − T (1)
Torque τ = TR = Iα =
1
2
mR
2
a
R
∴ T =
1
2
ma (2)
Using (2) in (1)
a =
2
3
g sin θ =
2
3
g sin 30
◦
=
g
3
4.41
<ω>=
ωdt
dt
(1)
τ = I α = C
√
ω
where C is a constant.

4.3 Solutions 171
∴ α = C
1
√
ω
where C
1
= constant
α =
dω
dt
= C
1
√
ω
∴ dt =
dω
C
1
√
ω
(2)
Using (2) in (1)
<ω>=
ω
0
0
√
ωdω
ω
0
0
dω
√
ω
=
ω
0
3
4.42 OC = L is the length of the rod with the centre of mass G at the midpoint,
Fig. 4.27. As the rod rotates with angular velocity ω it makes an angle θ with
the vertical OA through O. Drop a perpendicular GD = r on the vertical OA
and a perpendicular GB on OC.
r =
L
2
sin θ
The acceleration of the rod at G at any instant is ω
2
r = ω
2
(
L/2
)
sin θ , hori-
zontally and in the plane containing the rod and OA. The component at right
angles to OG is ω
2
(
L/2
)
sin θ cos θ and the angular acceleration α about O in
the vertical plane containing the rod and OA will be ω
2
sin θ cos θ
Torque mgr= mg
L
2
sin θ = Iα = m
L
2
3
ω
2
sin θ cos θ
mL
2
sin θ
g −
2L
3
ω
2
cos θ
= 0
θ = 0 or cos
−1
3g
2ω
2
L
If 3g > 2ω
2
L, i.e. ω
2
<
3g
2L
, the only possible solution is θ = 0, i.e. the rod
hangs vertically. If ω
2
>
3g
2L
, then θ = cos
−1
3g
2ω
2
L
.
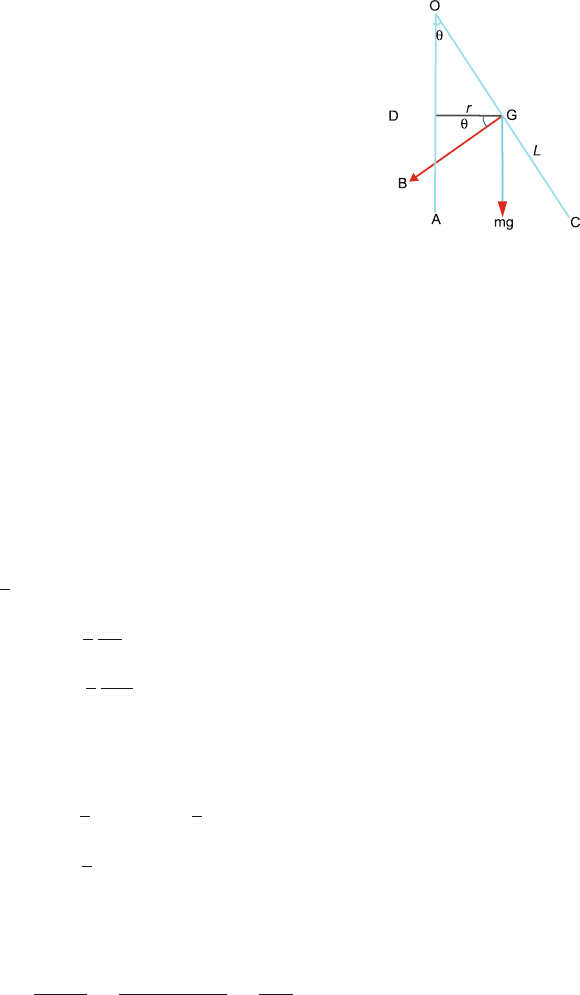
172 4 Rotational Dynamics
Fig. 4.27
4.43
(a) For pure sliding equation of motion is
ma =−μmg
or a =−μg (1)
v = v
0
− μgt (2)
At the instant pure rolling sets in
Torque Iα = FR (3)
2
5
mR
2
α = μmg R
∴ α =
5
2
μg
R
(4)
ω = αt =
5
2
μgt
R
(5)
Using (5) in (2)
v = v
0
−
2
5
ωR = v
0
−
2
5
v
∴ v =
5
7
v
0
(b) v = v
0
− μgt
t =
v
0
− v
μg
=
v
0
−
(
5/7
)
v
0
μg
=
2v
0
7μg
(c) v
2
= v
2
0
+ 2as

4.3 Solutions 173
= v
2
0
− 2μgs
5
7
v
0
2
= v
2
0
− 2μgs
s =
12
49
v
2
0
μg
The assumption made is that we have either pure sliding or pure rolling.
Actually in the transition both may be present.
4.44 L = r × p
Differentiating
dL
dt
= r ×
d p
dt
+ p ×
dr
dt
= r × F + p ×v = τ + 0 = τ
because the momentum and velocity vectors are in the same direction.
Angular momentum conservation requires that
|
L
i
|
=
|
L
f
|
= mv
l
2
L = (l/2)mv is not correct because L is perpendicular to v.
L conservation gives
mv
l
2
=
1
3
Ml
2
ω + mω
l
2
4
∴ ω =
6mv
(4M + 3m)l
(1)
K
rot
=
1
2
Iω
2
+
1
2
m
ωl
2
2
=
3m
2
v
2
2(4M + 3m)
wherewehaveused(1).
∴
K
rot
1
2
mv
2
=
3m
4M + 3m
=
3
23
where we have used M = 5m (by problem).
4.45 Let the small sphere break off from the large sphere at angle θ with the verti-
cal, Fig. 4.28. At that point the component of (gravitational force) – (centrifu-
gal force) = reaction = 0
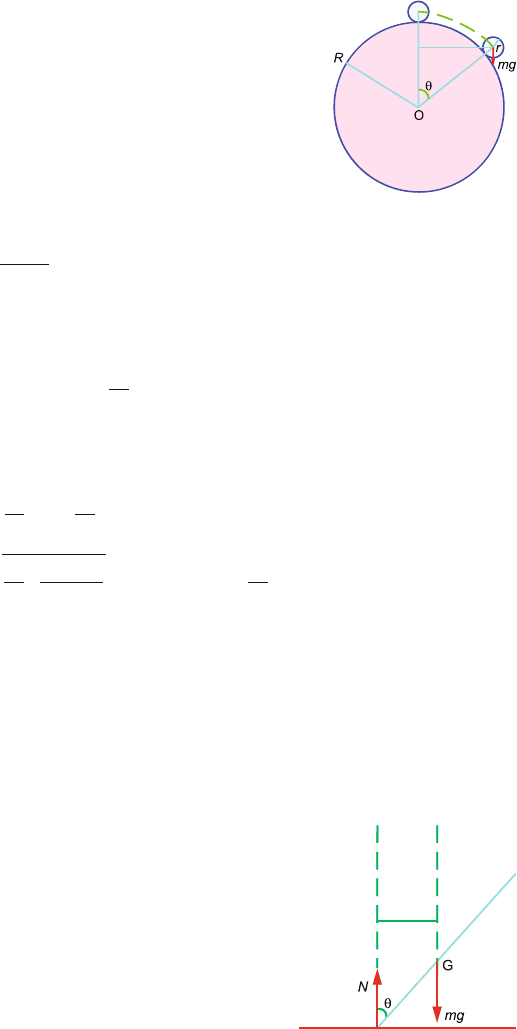
174 4 Rotational Dynamics
Fig. 4.28
mg cos θ =
mv
2
R +r
(1)
Loss in potential energy = gain in kinetic energy
mg(R + r)(1 − cos θ) =
7
10
mv
2
(2)
Solving (1) and (2)
g(R +r) =
17
10
v
2
=
17
10
ω
2
r
2
∴ ω =
10
17
g
(R +r)
r
2
and θ = cos
−1
10
17
4.46 Let N be the reaction of the floor and θ the angle which the r od makes with
the vertical after time t,Fig.4.29. The only forces acting on the rod are the
weight and the reaction which act vertically and consequently the centre of
mass moves in a straight line vertically downwards.
Equation of motion for the centre of mass is
Fig. 4.29
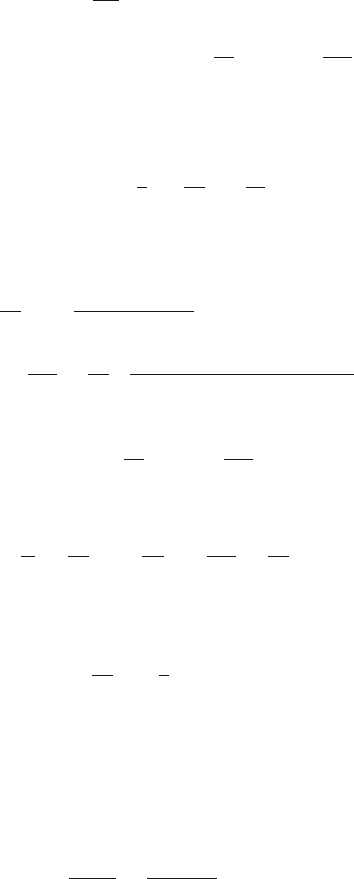
4.3 Solutions 175
mg − N = m
d
2
dt
2
(a − a cos θ)
or mg − N = ma
cos θ
dθ
dt
2
+ sin θ
d
2
θ
dt
2
!
(1)
The work–energy theorem gives
mga(1 −cos θ) =
1
2
m
dθ
dt
2
a
2
3
+ a
2
sin
2
θ
where the square bracket has been written using the parallel axis theorem.
dθ
dt
2
=
6g(1 − cos θ)
a(1 + 3sin
2
θ)
(2)
∴
d
2
θ
dt
2
=
3g
a
sin θ(7 − 6 cos θ −3sin
2
θ)
(1 + 3sin
2
θ)
2
!
(3)
By substituting
dθ
dt
2
and
d
2
θ
dt
2
from (2) and (3) in (1), the reaction N is
obtained as a function of θ . When the rod is about to strike the floor,
θ =
π
2
;
dθ
dt
2
=
3g
2a
and
d
2
θ
dt
2
=
3g
4a
Thus the reaction from (1) will be
N = m
g −
3g
4
or
1
4
mg
4.47
(a) For α
net
= 0, the two torques which act in the opposite sense must be
equal (Fig. 4.30), i.e.
τ
1
= τ
2
or m
1
gR
1
= m
2
gR
2
m
2
=
m
1
R
1
R
2
=
25 × 1.2
0.5
= 60 kg
(b)
(i)
a
1
= α R
1
, a
2
= α R
2
(1)
as R
1
> R
2
, a
1
> a
2
(ii) Equations of motion are
176 4 Rotational Dynamics
m
1
a
1
= m
1
g − T
1
(2)
m
2
a
2
= T
2
− m
2
g (3)
T
1
R
1
− T
2
R
2
= I α (4)
Combining (1), (2), (3) and (4) and substituting m
1
= 35 kg, m
2
= 60 kg,
R
1
= 1.2m, R
2
= 0.5m, I = 38 kg m
2
and g = 9.8m/s
2
, we find
a
1
=
(m
1
R
1
− m
2
R
2
)R
1
g
m
1
R
2
1
+ m
2
R
2
2
+ I
=
(35 × 1.2 − 60 × 0.5)1.2g
35 × 1.2
2
+ 60 × 0.5
2
+ 38
= 0.139g
a
2
= a
1
R
2
R
1
= 0.139 ×
0.5
1.2
= 0.058 g
T
1
= m
1
(g −a
1
) = 35g(1 − 0.139) = 295.3N
T
2
= m
2
(g +a
2
) = 60g(1 + 0.058) = 622.1N
α =
T
1
R
1
− T
2
R
2
I
=
295.3 × 1.2 − 622.1 × 0.5
38
= 1.14 rad/s
2
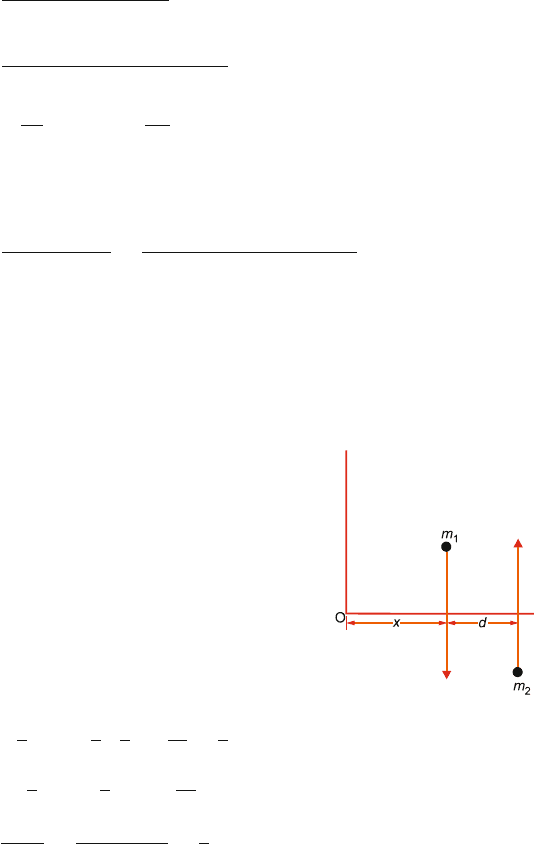
4.48
J = J
1
+ J
2
= x
ˆ
i ×(−mv
ˆ
j) + (x + d)
ˆ
i ×(mv
ˆ
j)
= mvd
ˆ
i ×
ˆ
j = mvd
ˆ
k
which is independent of x and therefore independent of the origin.
Fig. 4.30
4.49
(a)
K
rot
=
1
2
Iω
2
=
1
2
·
2
5
mr
2
v
2
r
2
=
1
5
mv
2
K
total
=
1
2
mv
2
+
1
5
mv
2
=
7
10
mv
2
∴
K
rot
K
total
=
(
1/5
)
mv
2
(
7/10
)
mv
2
=
2
7
