Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book

Подождите немного. Документ загружается.

4.2 Problems 147

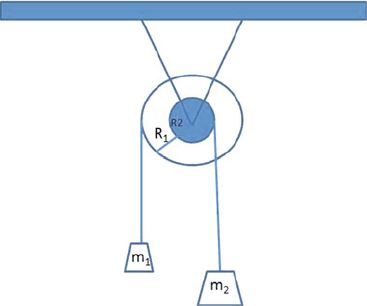
(i) For each mass, write down the relationship between its linear acceleration

and the angular acceleration of the pulley. Which mass has the greater

linear acceleration?

(ii) Determine the angular acceleration of the double pulley and the tensions

in both ropes.

[University of Manchester 2008]

Fig. 4.12

4.48 Two particles, each of mass m and speed v, travel in opposite directions along

parallel lines separated by a distance d. Show that the vector angular momen-

tum of this system of particles is independent of origin.

4.49 A small sphere of mass m and radius r rolls without slipping on the inside of

a large hemisphere of radius R, the axis of symmetry being vertical. It starts

from rest. When it arrives at the bottom show that

(a) the fraction K(rot)/K (total) = 2/7

(b) the normal force exerted by the small sphere is given by N = 17mg/7

4.50 A solid sphere, a hollow sphere, a solid disc and a hoop with the same mass

and radius are spinning freely about a diameter with the same angular speed

on a table. For which object maximum work will have to be done to stop it?

4.51 In prob. (4.50) the four objects have the same angular momentum. For which

object maximum work will have to be done to stop it?

4.52 In prob. (4.50) the four objects have the same angular speed and same angular

momentum. Compare the work to be done to stop them.

4.53 A solid sphere, a hollow sphere, a solid cylinder and a hollow cylinder roll

down an incline. For which object the torque will be least?

4.54 A particle moves with the position vector given by r = 3t

i + 2

j. Show that

the angular momentum about the origin is constant.

148 4 Rotational Dynamics

4.55 A metre stick of length l and mass M is placed on a frictionless horizontal

table. A hockey ball of mass m sliding along the table perpendicular to the

stick with speed v strikes the stick elastically at distance d from the centre of

the metre stick. Find d if the ball is to be brought to rest immediately after the

collision (Fig. 4.13).

Fig. 4.13

4.56 A uniform solid cylinder of mass m and radius R is set in rotation about its

axis and lowered with the lateral surface on to the horizontal plane with initial

centre of mass velocity v

. If the coefﬁcient of friction between the cylinder

and the plane is μ, ﬁnd

(a) how long the cylinder will move with sliding friction.

(b) the total work done by the sliding friction force on the cylinder.

4.57 Two identical cylinders, each of mass m, on which light threads are wound

symmetrically are arranged as in Fig. 4.14. Find the tension of each thread in

the process of motion. Neglect the friction in the axle of the upper cylinder.

Fig. 4.14

4.58 A uniform circular disc of radius r and mass m is spinning with uniform

angular velocity ω in its own plane about its centre. Suddenly a point on its

circumference is ﬁxed. Find the new angular speed ω



and the impulse of the

blow at the ﬁxed point.

4.2 Problems 149

4.59 A uniform thin rod of mass m and length L is rotating on a smooth horizontal

surface with one end ﬁxed. Initially it has an angular velocity  and the motion

slows down only because of air resistance which is k dx times the square of

the velocity on each element of the rod of length dx. Find the angular velocity

ω after time t.

4.60 A sphere of radius a oscillates at the bottom of a hollow cylinder of radius b

in a plane at right angles to the axis which is horizontal. If the cylinder is ﬁxed

and the sphere does not slide, ﬁnd T , the time period of oscillations in terms

of a, b and g, the acceleration due to gravity.

4.61

(a) Show that the moment of inertia of a disc of radius R and mass M about

an axis through the centre perpendicular to its plane is

I =

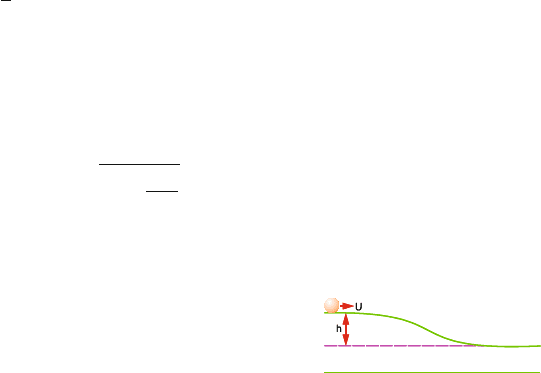
(b) A disc rolls without slipping along a horizontal surface with velocity u.

The disc then encounters a smooth drop of height h, after which it con-

tinues to move with velocity v. At all times the disc remains in a vertical

plane (Fig. 4.15).

Show that v =



4gh

[University of Manchester 2008]

Fig. 4.15

4.62 A circular ring of mass m and radius r lies on a smooth horizontal surface. An

insect of mass m sits on it and crawls round the ring with a uniform speed v

relative to the ring. Obtain an expression for the angular velocity of the ring.

[With courtesy from R.W. Norris and W. Seymour, Longmans,

Green and Co., 1923]

4.2.3 Coriolis Acceleration

4.63

(a) Given that earth rotates once every 23 h 56 min around the axis from the

North to South Pole, calculate the angular velocity, ω, of the earth. When

viewed from above the North Pole, the earth rotates counterclockwise

(west to east). Which way does ω point?

150 4 Rotational Dynamics

(b) Foucault’s pendulum is a simple pendulum suspended by a long string

from a high ceiling. The effect of Coriolis force on the motion of the

pendulum is to produce a precession or rotation of the plane of oscillation

with time. Find the time for one rotation for the plane of oscillation of the

Foucault pendulum at 30

◦

latitude.

4.64 An object is dropped at the equator from a height of 400 m. How far does it

hit the earth’s surface from a point vertically below?

4.65 An object at the equator is projected upwards with a speed of 20 m/s. How far

from its initial position will it land?

4.66 With what speed must an object be thrown vertically upwards from the surface

of the earth on the equator so that it returns to the earth 1 m away from its

original position?

4.67 A body is dropped from a height at latitude λ in the northern hemisphere.

Show that it strikes the ground a distance d =

ω cos λ



to the west,

where ω is the earth’s angular velocity.

4.68 An iceberg of mass 5 × 10

tons near the North Pole moves west at the rate

of 8 km/day. Neglecting the curvature of the earth, ﬁnd the magnitude and

direction of the Coriolis force.

4.69 A tidal current is running due north in the northern latitude λ with velocity

v in a channel of width b. Prove that the level of water on the east coast is

raised above that on the western coast by (2bvω sin λ)g where ω is the earth’s

angular velocity.

4.70 If an object is dropped on the earth’s surface, prove that its path is a semicu-

bical parabola, y

= z

4.71 A train of mass 1000 tons moves in the latitude 60

◦

north. Find the magnitude

and direction of the lateral force that the train exerts on the rails if it moves

with a velocity of 15 m/s.

4.72 Atrainofmassm is travelling with a uniform velocity v along a parallel

latitude. Show that the difference between the lateral force on the rails when

it travels towards east and when it travels t owards west is 4mvω cos λ, where

λ is latitude and ω is the angular velocity of the earth.

4.73 A body is thrown vertically upwards with a velocity of 100 m/s at a 60

◦

lati-

tude. Calculate the displacement from the vertical in 10 s.

4.3 Solutions 151

4.3 Solutions

4.3.1 Moment of Inertia

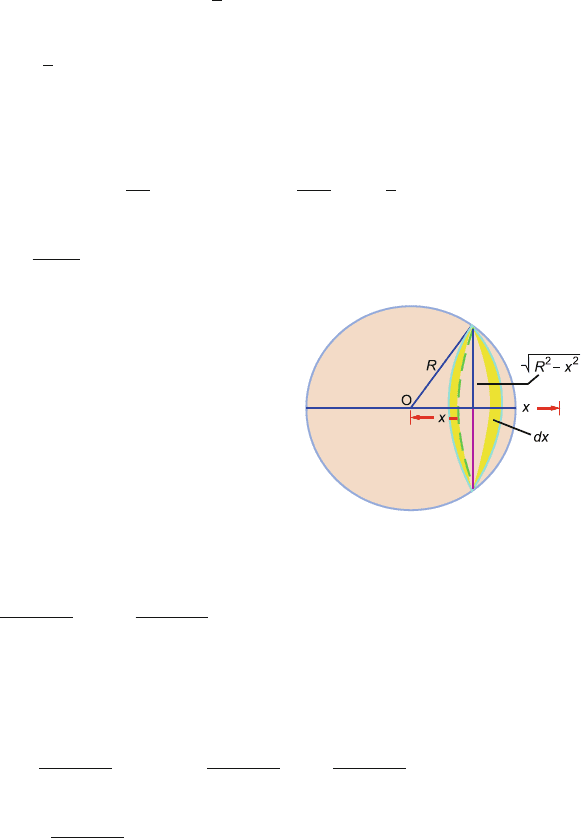
4.1 Imagine the sphere of mass M and radius R to be made of a series of circu-

lar discs, a typical one being of thickness dx at distance x from the centre,

Fig. 4.16. The area of the disc is π(R

−x

), and if the density of the sphere is

ρ, the mass of the disc is ρπ(R

− x

) dx. The elementary moment of inertia

of the disc about the axis OX is

(mass)(radius)

∴ dI =

πρ (R

− x

)dx(R

− x

)

Hence the moment of inertia of the sphere is

I =



dI =



πρ

− x

)

dx =

8πρ

as ρ =

4π R

Fig. 4.16

4.2 Let the mass m

and m

be at distance r

and r

, respectively, from t he centre

of mass. Then

+ m

, r

+ m

Moment of inertia of the masses about the centre of mass is given by

I = m

+ m

= m



+ m



+ m



+ m



+ m

= μ r

where μ =

+ m

152 4 Rotational Dynamics

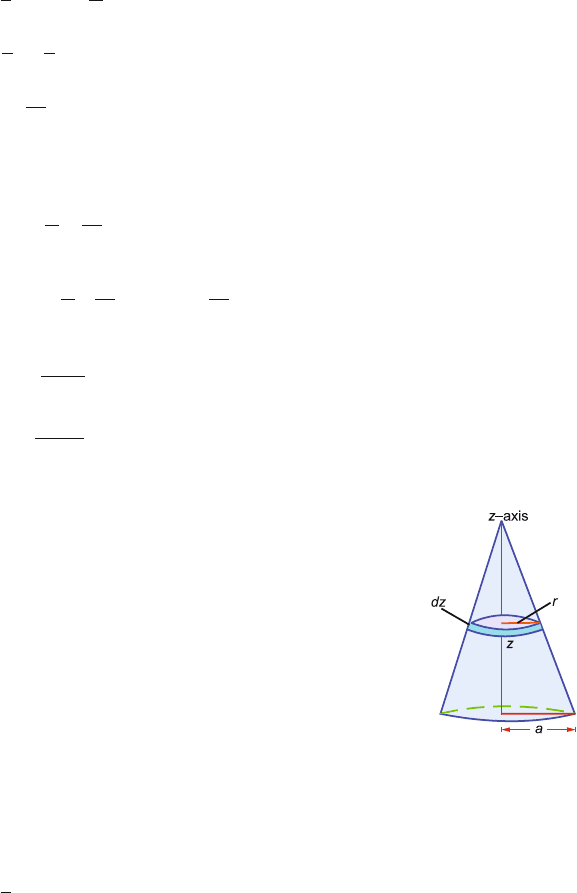
4.3 Consider the cone to be made up of a series of discs, a typical one of radius r

and of thickness dz at distance z from the apex. Volume of the disc is dV =

πr

dz. Its mass will be dm = ρdV = πρr

dz, where ρ is the mass density

of the cone. The moment of inertia dI of the disc about the z-axis is given by

(Fig. 4.17)

dI =

dm =

ρr

But

(from the geometry of the ﬁgure)

or r =

where h is the height of the cone and a is the radius of the base

∴ dI =

I =



dI =



dz =

ρ a

But ρ =

πa

∴ I =

3Ma

Fig. 4.17

4.4 Consider a slice of the cylinder of thickness dz at distance z from the centre of

mass of cylinder O. The moment of inertia about an axis passing through the

centre of the slice and perpendicular to z-axis will be

dI =

dmR

4.3 Solutions 153

Fig. 4.18

Then the moment of inertia about an axis parallel to the slice and passing

through the centre of mass is given by the parallel axis theorem, Fig. 4.18.

dmR

+ dmz

= π R



+ z



where dm = π R

ρdz is the mass of the slice and ρ is the density.

∴ I



= π R

+h/2



−h/2



+ z



= π R



h +



But ρ =

π R

∴ I



+ h



4.5 The moment of inertia of the larger solid sphere of mass M

(1)

The moment of inertia of the smaller solid sphere of mass m, which is removed

to hollow the sphere, is

(2)

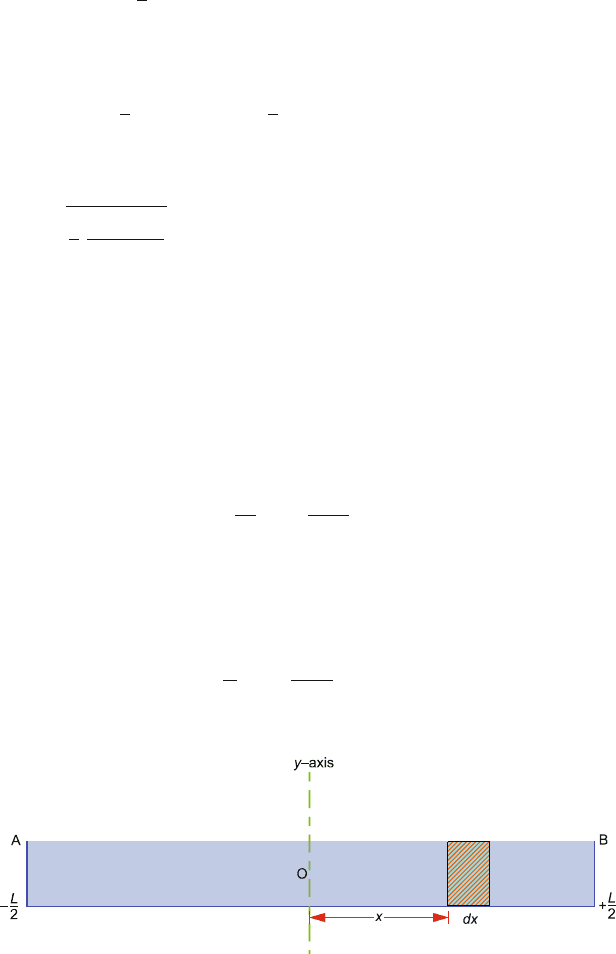
154 4 Rotational Dynamics

As the axis about which the moment of inertia is calculated is common to both

the spheres, the moment of inertia of the hollow sphere will be

I = I

− I

(Ma

− mb

) = (M −m)k

(3)

where (M −m) is the mass of the hollow sphere and k is the radius of gyration.

Now M =

π a

ρ and m =

π b

ρ (4)

Using (4) in (3) and simplifying we get

k =



− b

)

− b

)

4.6

(a) Let AB represent a thin rod of length L and mass M,Fig.4.19. Choose the

x-axis along length of the rod and y-axis perpendicular to it and passing

through its centre of mass O. Consider a differential element of length dx

at a distance x from O. The mass associated with it is M

(

dx/L

)

.The

contribution to moment of inertia about the y-axis by this element of length

will be M

(

dx/L

)

. The moment of inertia of the rod about y-axis passing

through the centre of mass is



+L/2



−L/2

(b) Moment of inertia about y-axis passing through the end of the rod (A or B)

is given by the parallel axis theorem:

= I

+ M





Fig. 4.19

4.3 Solutions 155

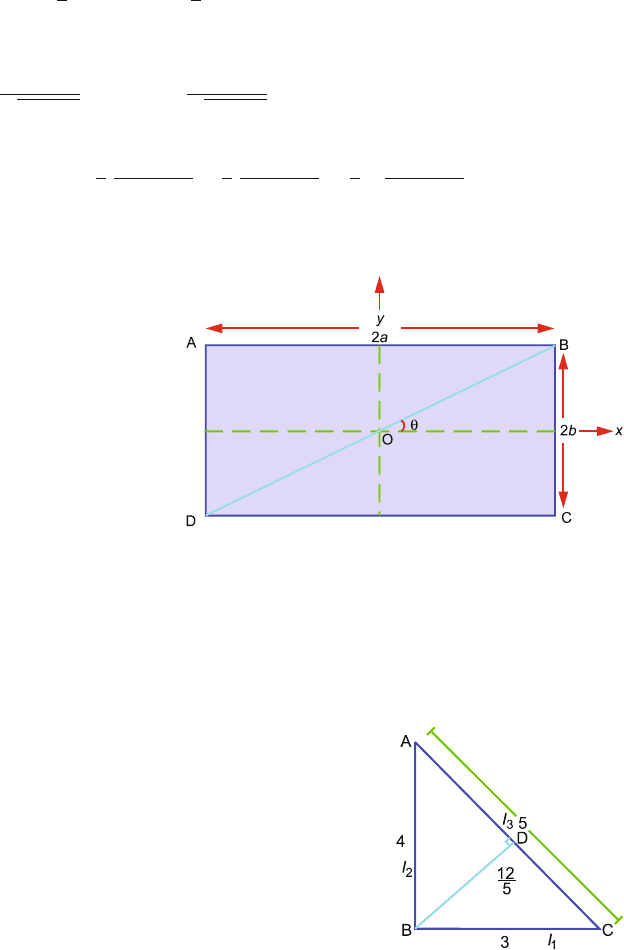
4.7 The moment of inertia of the plate about x-axis is I

(

1/3

)

and about

y-axis is I

(

1/3

)

. It can be shown that the moment of inertia about the

line BD is

cos

θ +

sin

θ (1)

where θ is the angle made by BD with the x-axis. From Fig. 4.20, cos θ =

√

+ b

and sin θ =

√

+ b

∴ I



+ b





+ b





+ b



Fig. 4.20

4.8 The moment of inertia about any side of a triangle is given by the product of

the one-sixth mass m of the triangle and the square of the distance (p) from the

opposite vertex, i.e. I = mp

/6. The perpendicular BD on AC is found to be

equal to 12/5 from the geometry of Fig. 4.21.

Fig. 4.21

156 4 Rotational Dynamics

(AB)

(BC)

(BD)





24m

∴ I

> I

4.9 If the radius of the sphere is r then the volume of the sphere must be equal to

that of the disc:

π r

= π R

∴ r =

The moment of inertia of the disc I = I

(

1/2

)

The moment of inertia of the sphere

4.10 Consider a strip of radius r on the surface of the sphere symmetrical about the

z-axis and width Rdθ, where R is the radius of the hollow sphere, Fig. 4.22.

Fig. 4.22

Area of the strip is 2πr · Rd θ = 2π R

sin θ d θ.Ifσ is the surface mass den-

sity (mass per unit area) then the mass of the strip is dm = 2π R

σ sin θ d θ .

Moment of inertia of the elementary strip about the z-axis

dI = dmr

= 2π R

σ sin

θ d θ

Moment of inertia contributed by the entire surface will be