Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book

Подождите немного. Документ загружается.

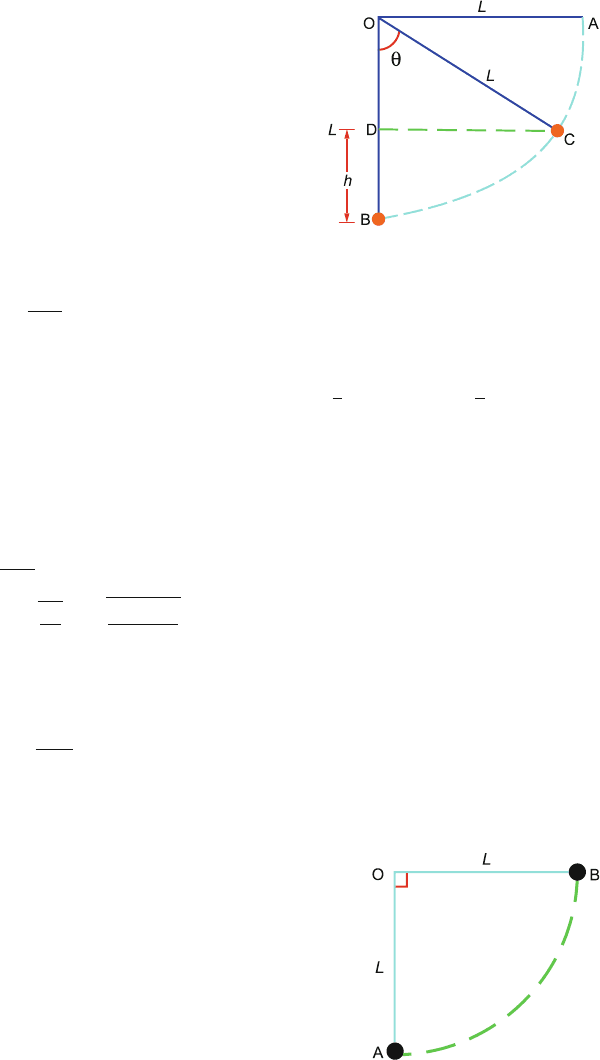
126 3 Rotational Kinematics

Fig. 3.17

The tension in the string at C will be

T =

+ mg cos θ (3)

By problem, T = mg (4)

Combining (2), (3) and (4) we get cos θ =

or θ = cos

−1





3.29 At the top of the sphere, v is in the horizontal direction and the frictional force

acts upwards. The condition that the motorcyclist may not fall is

Friction force = Weight

= mg

v =



9.8 × 10

0.8

= 11 m/s

3.30 At the lowest point A, Fig. 3.18, the tension in the string is

+ mg (1)

where v

is the velocity at point A.

Fig. 3.18

3.3 Solutions 127

Measure potential energy with respect to A, the equilibrium position. At the

point B, at height L the mechanical energy is entirely potential energy as the

bob is at rest. As the vertical height is L, the potential energy will be mgL.

When the bob is released, at the point A, the energy is entirely kinetic, poten-

tial energy being zero, and is equal to

Conservation of mechanical energy requires that

= mg L

or v

= 2 gL (2)

Using (2) in (1)

= 2mg + mg = 3mg

Thus the minimum strength of the string that it may not break upon passing

through the lowest point is three times the weight of the bob.

3.31 Let the ball be deﬂected through a small angle θ from the equilibrium

position A, Fig. 3.19.

θ =

(1)

Fig. 3.19

where s is the corresponding arc. Drop a perpendicular BC on AO, so that the

height through which the bob is raised is AC = h.

Now, h = AC = OA − OC = L − L cos θ = L(1 −cos θ)

= L



1 − 1 +

+···



∴ h =

Lθ

(2)

where we have used (1).

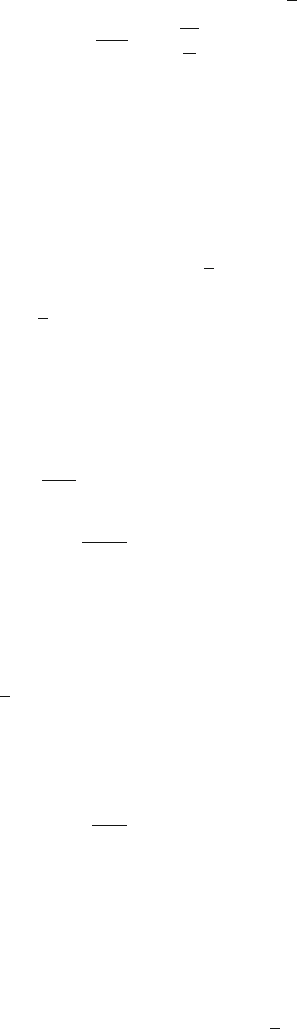
128 3 Rotational Kinematics

From energy conservation, mgh =

∴ v =



2gh = s



3.32 In coming down from angular displacement of 60

◦

to 45

◦

, loss of potential

energy is given by

mg(h

− h

) = mg L(1 −cos 60

◦

) − mg L(1 −cos 45

◦

)

= 0.207 mg L

Gain in kinetic energy =

∴

= 0.207 mg L = 0.207 mg (∵ L = 1m)

or v = 2.014 m/s

The tension in the string would be

T =

+ mg cos 45

◦

= mg



4.056

+ 0.707



N = 1.12 mg N

3.33 When the bob is displaced through angle θ, the potential energy is mg L(1 −

cos θ). At the lowest position the energy is entirely kinetic

= mg L (1 −cos θ) (1)

The tension in the string will be

T = mg +

= mg + 2mg (1 −cos θ) (2)

where we have used (1)

By problem

T = 2mg (3)

From (2) and (3) we ﬁnd cos θ =

or θ = 60

◦

3.3 Solutions 129

3.3.3 Loop-the-Loop

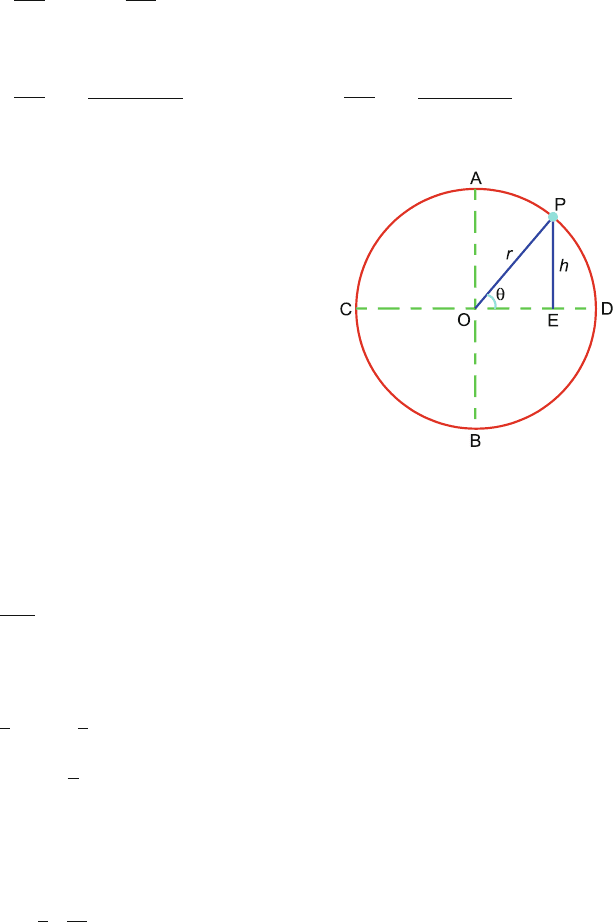
3.34 If the bob of the pendulum has velocity u at B, the bottom of the vertical circle

of radius r such that



2gr < u <



5gr (1)

then the bob would leave some point P on the are DA (Fig. 3.20). Here



2gr =

√

2 × 9.8 × 1 = 4.427 m/s and



5gr =

√

5 × 9.8 × 1 = 7m/s

Fig. 3.20

Therefore (1) is satisﬁed for u = 6m/s.

Drop a perpendicular PE on the horizontal CD. Let PE = h and PO make an

angle θ with OD. When the bob leaves the point P, the normal reaction must

vanish.

− mg sin θ = 0(2)

Loss in kinetic energy = gain in potential energy

−

= mg(h +r) (3)

sin θ =

(4)

Eliminating v

between (2) and (3) and using (3), with u = 6m/s and

r = 1.0m,

h =



− 2r



= 0.558 m

130 3 Rotational Kinematics

3.35 Let the height of the incline be h. Then the velocity of the block at the bottom

of the vertical circle will be v =

√

2gh . Minimum height is given by the

condition that v =

√

5gr which is barely needed for the completion of the

loop.



2gh =



5gr

or h =

r =

× 12 = 30 cm

3.36 The analysis is similar to that of prob. (2.34). The velocity of the particle at

the bottom of the circular groove will be given by

v =



(2g)(2r) =



4gr (1)

which satisﬁes the condition



2gr < u <



5gr

The particle leaves the circular groove at a height h above the centre of the

circle, Fig. 3.20.

h =



− 2r



(2)

But u

= 4gr (1)

∴ h =

Thus, the particle leaves the circular groove at a height of h + r =

r above

the lowest point.

3.37 Let the velocity at B be v.

Kinetic energy gained = potential energy lost

= mg(5R − R)

∴ m

= 8 mg

which is the centrifugal force acting on the track horizontally. The weight acts

vertically down. Hence the resultant force

F =



(8 mg)

+ (mg)

√

65 mg

3.3 Solutions 131

3.38 Gain in kinetic energy = loss of potential energy

= mg(h −2R)

= 2g (h − 2R) (1)

The force exerted on the track at the top

F =

− mg (2)

By problem

F = mg (3)

∴

− mg = mg

or v

= 2gR (4)

Using (4) in (1) we ﬁnd h = 3R.

3.39 Let the particle velocity at the lowest position be u = 0.8944

√

5gR and v at

point P.

Loss in kinetic energy = gain in potential energy

−

= mg(R + R sin θ)

or v



0.8944



5gR



− 2 gR(1 + sin θ) (1)

The particle would leave at P (Fig. 3.7) when

= mg sin θ

or v

= gR sin θ (2)

Using (2) in (1) and solving

sin θ = 2/3orθ = 41.8

◦

3.40 Let the minimum height be h. The velocity of the block at the beginning of

the circular track will be

v =



2gh (1)

For completing the circular track

v =



5gR (2)

132 3 Rotational Kinematics

From (1) and (2)

h = 2.5R

3.41 Let the nail be located at D at distance x vertically below A, the point of

suspension, Fig. 3.21. Initially the bob of the pendulum is positioned at B at

height h above the equilibrium position C.

h = L(1 − cos θ) = L(1 −cos 60

◦

) =

L (1)

Fig. 3.21

where L = 1 m is the length of the pendulum. When the pendulum is released

its velocity at C will be

v =



2gh =



gL (2)

The velocity needed at C to make complete revolution in the vertical circle

centred at the nail and radius r is

v =



5gr (3)

From (2) and (3)

r =

L (4)

Therefore x = AD = AC − DC = L −

= 0.8 L

= 0.8 ×1m= 80 cm

3.42 If M and m are the mass of the test tube and cork, respectively, and their

velocity V and υ respectively, momentum conservation gives

3.3 Solutions 133

MV = mv (1)

or v =

V =

V = 10 V (2)

Condition for describing a full vertical circle is that the minimum velocity of

the test tube should be

V =



5gr =

√

5 × 980 × 5 = 156.5cm/s

Therefore the minimum velocity of the cork which ﬂies out ought to be

v = 10 V = 1565 cm/s = 15.65 m/s

3.43 Equating centripetal force to frictional force

= μ mg

μ =

(14)

9.8 × 45

Chapter 4

Rotational Dynamics

Abstract Chapter 4 is concerned with the moment of inertia and rotational motion

on horizontal and inclined planes and Coriolis acceleration.

4.1 Basic Concepts and Formulae

Moment of Inertia/Rotational Inertia (M.I.) or (I)

Table 4.1 Moments of inertia (M.I.) of some regular bodies

Body Axis M.I.

Thin rod of length L Perpendicular to length through centre mL

/12

Perpendicular to length at one end mL

Thin rectangular sheet of sides

a and b

Through centre parallel to side bma

/12

Through centre perpendicular to sheet m(a

+ b

)/12

Thin hoop Through centre perpendicular to plane

of ring

Through centre along diameter mr

Thin circular disc Through centre perpendicular to disc mr

Solid sphere of radius r About any diameter 2mr

Thin spherical shell About any diameter 2mr

Right cone of radius of base r Along axis of cone 3mr

/10

Circular cylinder of length L

and radius R

Through centre perpendicular to axis m





Table 4.2 Translational and rotational analogues

Quantity Translation Rotation

Displacement s θ

Velocity v = ds/dt ω = dθ/dt

Acceleration a = dv/dt α = dω/dt

Mass/inertia mI

Momentum p = mv J = I ω

Impulse J = Ft J = τ t

Work W = Fs W = τθ

135

136 4 Rotational Dynamics

Table 4.2 (continued)

Quantity Translation Rotation

Kinetic energy K =

K =

Iω

Power P = Fv P = τω

Newton’s second law F = ma τ = I α

Equilibrium condition



ext

= 0



ext

= 0

Kinematics v = u + at ω = ω

+ αt

= u

+ 2as ω

= ω

+ 2αθ

s = ut +

θ = θ

t +

αt

s =

(u + v)t θ =

(ω

+ ω)t

The Perpendicular Axes Theorem

The sum of the moments of inertia of a plane lamina about any two perpendicular

axes in its plane is equal to its moment of inertia about an axis perpendicular to its

plane and passing through the point of intersection of the ﬁrst two axes:

= I

+ I

(4.1)

The theorem is valid for plane lamina only.

The Parallel Axes Theorem

The M.I. of a body about any axis is equal to the sum of its M.I. about a parallel axis

through the centre of mass and the product of its mass and the square of the distance

between the two axes.

Conservation of angular momentum (J) implies

J = I

= I

(4.2)

Motion of a body rolling down an incline of angle θ:

a =

g sin θ

1 +

(4.3)

where I = Mk

and k is known as the radius of gyration.

t =



(4.4)

total

= K

trans

+ K

rot



1 +



(4.5)