Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.


4.3 Solutions 177
(b) In coming down to the bottom of the hemisphere loss of potential
energy = mgh = mg R. Gain in kinetic energy =
(
7/10
)
mv
2
.
∴
7
10
mv
2
= mgR
or
mv
2
R
=
10mg
7
The normal force exerted by the small sphere at the bottom of the large
sphere will be
N = mg +
mv
2
R
= mg +
10mg
7
=
17mg
7
4.50 Work done W = τθ = I αθ =
Iω
2
2
Along the diameter for hoop, I = mR
2
/2, while for the solid sphere, hollow
sphere and the disc, I =
(
2/5
)
mR
2
,
(
2/3
)
mR
2
and
(
1/4
)
mR
2
, respectively,
maximum work will have to be done to stop the hollow sphere, ω being iden-
tical as it has the maximum moment of inertia.
4.51 Work done W = τθ = I αθ =
Iω
2
2
=
J
2
2I
where we have used the formula J = I ω. Maximum work will have to be
done for the disc since I is the least, τ being identical.
4.52
W =
1
2
Iω
2
=
1
2
(I ω)ω =
1
2
Jω
Since J and ω are the same for all the four objects, work done is the same.
4.53
τ = Iα = I
a
R
=
MgR sin θ
1 +
R
2
/k
2
For solid sphere, hollow sphere, solid cylinder and hollow cylinder the quan-
tity 1 + (R
2
/k
2
) is 7/2, 5/2, 3, 2, respectively. Therefore τ will be least for
solid sphere.
178 4 Rotational Dynamics
4.54 r = 3t
ˆ
i +2
ˆ
j
v =
dr
dt
= 3
ˆ
i
L = r × p = m(r × v) = m(3t
ˆ
i +2
ˆ
j) × 3
ˆ
i
= 6 m(
ˆ
j ×
ˆ
i) =−6 m
ˆ
k (constant)
4.55 Angular momentum conservation gives
J = mvd = I ω (1)
Linear momentum conservation gives
mv = Mv
c
(2)
Energy conservation gives
1
2
mv
2
=
1
2
Iω
2
+
1
2
Mv
2
c
(3)
I =
Ml
2
12
(4)
Eliminating ω and v
c
from (1) and (2) and using (3)
1
2
mv
2
=
1
2
m
2
v
2
d
2
I
+
1
2
m
2
v
2
M
(5)
Simplifying and using (4) in (5)
d =
l
2
M − m
3m
4.56
(a) Let the initial velocity be v
0
, then at instant t the velocity
v = v
0
− at = v
0
− μgt (1)
Torque τ = Iα = FR
1
2
mR
2
α = μ mg R
α =
2μg
R
μgt =
α Rt
2
=
ωR
2
4.3 Solutions 179
Therefore (1) becomes
v = v
0
−
ωR
2
= v
0
−
v
2
∴ v =
2
3
v
0
(2)
Using (2) in (1)
2
3
v
0
= v
0
− μ gt
or t =
v
0
3 μg
(b) Work done W = K =
1
2
mv
2
−
1
2
mv
2
0
=
1
2
m
4
9
v
2
0
− v
2
0
=−
5
18
mv
2
0
4.57 Equation of motion is
ma = mg −2T (1)
where ‘a’ is the linear acceleration and T the tension in each thread.
Torque Iα = 2Tr (∵ there are two threads)
1
2
mr
2
α = 2Tr
or α =
4T
mr
(2)
As both the cylinders are rotating,
a = 2αr =
8T
m
(3)
or ma = 8T (4)
Using (4) in (1) we get
T =
1
10
mg

180 4 Rotational Dynamics
Note that if the lower cylinder is not wound then
a =
4T
m
and T =
1
6
mg
4.58 C is the centre of the disc and A the point which is fixed, Fig. 4.31. The forces
acting at A have no torque at A, so that the angular momentum is conserved.
Initially the moment of inertia of the disc about the axis passing through its
centre and perpendicular to its plane is
I
c
= I =
1
2
mr
2
(1)
When the point A is fixed the moment of inertia about an axis parallel to t he
central axis and passing through A will be
I
A
= I
c
+ mr
2
= m
1
2
r
2
+r
2
=
3
2
mr
2
(2)
by parallel axis theorem.
Angular momentum conservation requires
I
A
ω
= I
c
ω (3)
Substituting (1) and (2) in (3) we obtain
ω
=
ω
3
(4)
If X and Y are the impulses of the forces at A perpendicular and along
CA, then
X = mrω
= mr
ω
3
and Y = 0
Thus the impulse of the blow at A is mr
ω
3
at right angles to CA.
Fig. 4.31
4.3 Solutions 181
4.59 The torque of the air resistance on an element dx at distance x from the fixed
end, about this end, will be
dτ = k(ωx)
2
x dx = kω
2
x
3
dx
τ =
dτ =−kω
2
L
0
x
3
dx = Iα
i.e. −
kω
2
L
4
4
=
1
3
mL
2
dω
dt
∴ −3kL
2
dt = 4m
dω
ω
2
∴ −3kL
2
t =−
4m
ω
+C
where C is the constant of integration. Initial condition: when t = 0, ω = .
Therefore C =
4m
∴ −3kL
2
t = 4m
1
−
1
ω
∴ ω =
4m
4m + 3kL
2
t
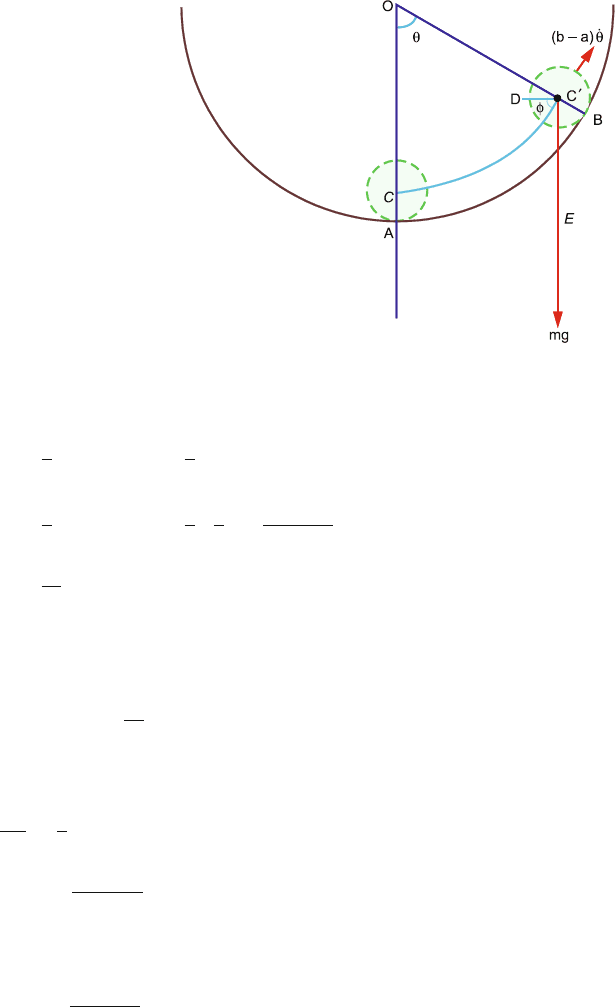
4.60 OA is the vertical radius b of the cylinder and a the radius of the sphere which
is vertical in the lowest position and shown as CA, Fig 4.32.
In the time the centre of mass of the sphere C has moved to C
through an
angle θ, the sphere has rotated through φ so that the reference lime CA has
gone into the place of C
D.
If there i s no slipping
a(φ +θ) = bθ (1)
The velocity of the centre of mass is (b −a)
˙
θ and the angular velocity of the
sphere about its centre is
˙
φ =
(b − a)
a
˙
θ (2)
Taking A as zero level, the potential energy
U = mg(b − a)(1 − cos θ) (3)
182 4 Rotational Dynamics
Fig. 4.32
The kinetic energy = T (trans) + T (rot)
T =
1
2
m(b − a)
2
˙
θ
2
+
1
2
I
˙
φ
2
=
1
2
m(b − a)
2
˙
θ
2
+
1
2
·
2
5
ma
2
(b − a)
2
a
2
˙
θ
2
=
7
10
m(b − a)
2
˙
θ
2
(4)
where we have used (2).
Total energy
E = T +U =
7
10
m(b − a)
2
˙
θ
2
+ mg(b − a)(1 − cos θ) = constant (5)
Differentiating with respect to time and cancelling common factors
dE
dt
=
7
5
m(b − a)
¨
θ ·
˙
θ + g sin θ ·
˙
θ = 0(6)
or
¨
θ +
5g
7(b − a)
sin θ = 0(7)
For small oscillation angles sin θ → θ.
∴
¨
θ +
5g θ
7(b − a)
= 0(8)
which is the equation for simple harmonic motion with frequency

4.3 Solutions 183
ω =
5g
7(b − a)
(9)
and time period
T = 2π
7(b − a)
5g
(10)
4.61 (a) Let the disc be composed of a number of concentric rings of infinitesi-
mal width. Consider a ring of radius r, width dr and surface density σ
(mass per unit area). Then its mass will be (2πrdr)σ . The moment of
inertia of the ring about an axis passing through the centre of the ring and
perpendicular to its plane will be
dI = (2πr dr)σ r
2
Then the moment of inertial of the disc
I =
dI = 2πσ
R
0
r
3
dr =
1
2
πσ R
4
(1)
If M is the mass of the disc, then
σ =
M
π R
2
(2)
∴ I =
1
2
MR
2
(3)
(b) The total kinetic energy T of the disc on the horizontal surface is
T (initial) =
1
2
Mu
2
+
1
2
Iω
2
=
1
2
Mu
2
+
1
2
·
1
2
MR
2
u
2
R
2
=
3
4
Mu
2
(4)
T (final) =
3
4
Mv
2
=
3
4
Mu
2
+ Mgh
by energy conservation
Solving,v=
u
2
+
4
3
gh
4.62 In Fig. 4.33, O is the centre of the ring, P the instantaneous position of the
insect and G the centre of mass of the system. Suppose the insect crawls

184 4 Rotational Dynamics
Fig. 4.33
around the ring in the counterclockwise sense. The only forces acting in a
horizontal plane are the reactions at P which are equal and opposite. Conse-
quently G will not move and the angular momentum about G which was zero
initially will remain zero throughout the motion due to its conservation.
m · PG(v − PGω) − I
G
ω = 0(1)
where ω is the angular velocity of the ring.
Now PG =
Mr
M + m
, OG =
mr
M + m
(2)
I
ω
= I
CM
+ M(OG)
2
= Mr
2
+ M
m
2
r
2
(M + m)
2
(3)
Using (2) and (3) in (1) and simplifying we obtain
ω =
mv
(M + 2m)r
(4)
4.3.3 Coriolis Acceleration
4.63
(a) ω points in the south to north direction along the rotational axis of the
earth.
ω =
2π
T
=
2π
86, 160
= 7.292 ×10
−5
rad/s
(b) The period of rotation of the plane of oscillation is given by
T
=
2π
ω
=
2π
ω sin λ
=
T
0
sin λ
=
24
sin 30
◦
= 48 h
4.3 Solutions 185
4.64 The object undergoes an eastward deviation through a distance
d =
1
3
ω cos λ
8h
3
g
=
1
3
× 7.29 × 10
−5
× cos 0
◦
8 × 400
3
9.8
= 0.1756 m
= 17.56 cm
4.65
y
=
4
3
u
3
g
2
ω cos λ
=
4
3
×
(20)
3
(9.8)
2
× 7.29 × 10
−5
cos 0
◦
= 0.0081 m = 8.1mm
4.66
y
=
4
3
u
3
g
2
ω cos λ, λ = 0
◦
u =
3y
g
2
4ω cos λ
1/3
=
3
4
×
1 × (9.8)
2
7.27 × 10
−5
1/3
= 99.7m/s
4.67 Consider two coordinate systems, one inertial system S and the other rotating
one S
, which are rotating with constant angular velocity ω
Acceleration in Acceleration in Coriolis centrifugal
inertial frame = rotating frame + acceleration + acceleration
d
2
r
dt
2
=
d
2
r
dt
2
+ 2ω ×
dr
dt
+ ω × ω × r
(1)
Let the k axis in the inertial frame S be directed along the earth’s axis. Let
the rotating frame S
be rigidly attached to the earth at a geographical lati-
tude λ in the northern hemisphere. Let the k
axis be directed outwards at the
latitude λ along the plumb line, whose direction is that of the resultant pass-
ing through the earth’s centre. With the choice of a right-handed system, the
i
-axis is in the southward direction and the j
-axis in the eastward direction,
Fig. 4.34. Assume g the acceleration due to gravity to be constant. It includes
the centrifugal term ω ×(ω × r) since g is supposed to represent the resultant
acceleration of a falling body at the given place.
d
2
r
dt
2
= g − 2ω × v
R
(2)
Since we are considering the fall of a body in the northern hemisphere, the
components of angular velocity are
ω
x
=−ω cos λ
ω
y
= 0
ω
z
= ω sin λ
⎫
⎬
⎭
(3)
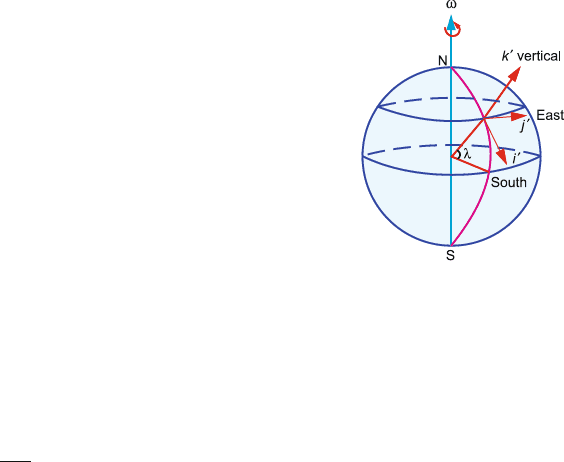
186 4 Rotational Dynamics
Fig. 4.34
ω × v
R
=
i
j
k
−ω cos λ 0 ω sin λ
˙x
˙y
˙z
=−ω sin λ ˙y
i
+ (ω sin λ ˙x
+ ω cos λ˙z
) j
− (ω cos λ ˙y
)k
But
d
2
r
dt
2
= g − 2(ω × v)
∴ ¨x
i
+¨y
j
+¨z
k
=−gk
+ 2ω sin λ ˙y
i
− 2(ω sin λ ˙x
+ ω cos λ˙z
) j
+ 2ω cos λ ˙y
k
(4)
Equating coefficients of i
, j
and k
on both sides of (4), we obtain the equa-
tions of motion
¨x
= 2ω sin λ ˙y
(5)
¨y
=−2(ω sin λ ˙x
+ ω cos λ˙z
) (6)
¨z
=−g + 2ω cos λ (7)
Now the quantities ˙x
and ˙y
are small compared to ˙z
. To the first approxima-
tion we can write
(v
R
)
x
= 0; (v
R
)
y
= 0; (v
R
)
z
=˙z
=−g (8)
Setting ˙x
=˙y
= 0 in (5), (6) and (7), we obtain the equations for the com-
ponents of a
R
:
(a
R
)
x
=¨x
= 0(9)
(a
R
)
y
=¨y
=−2ω ˙z
cos λ (10)
(a
R
)
z
=¨z
=−g (11)
Equation (9) shows that no deviation occurs in the north–south direction.
