Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.


5.3 Solutions 207
V (r) = V
1
+ V
2
(1)
The potential V
1
at P is the same as due to the mass of the sphere of radius r
concentrated at the centre O and is given by
V
1
=−G
4πr
3
3
ρ
r
=−
4
3
π Gr
2
ρ (2)
For the mass outside r, consider a typical shell at distance x from the centre
O and of thickness dx.
Volume of the shell = 4π x
2
dx
Mass of the shell = (4π x
2
dx)ρ
Potential due to this shell at the centre or at any point inside the shell, including
at P, will be
dV
2
=−
4πρx
2
dx
x
=−4π Gρx dx (3)
Potential V
2
at P due to the outer shells (x > r) is obtained by integrating (3)
between the limits r and a.
V
2
=
dV
2
=−4π Gρ
a
r
x d x =−2π Gρ(a
2
−r
2
) (4)
Using (2) and (4) in (1) and using ρ =
3M
4πa
3
V (r) =−
GM
2a
3 −
r
2
a
2
(5)
The potential (5) is that of a simple harmonic oscillator as the force
F =−
dV
dr
=−
GMr
a
3
i.e. the force is opposite and proportional to the distance.
5.12 Consider a length element dx of a thin rod of length L, at distance x from P
(Fig. 5.11). The mass element is
(
M/L
)
dx. The potential at P due to this mass
length will be
dV =−
GM
L
dx
x

208 5 Gravitation
Fig. 5.11
The potential at p from the entire r od is given by
V =
dV =−
GM
L
d+
L
2
d−
L
2
dx
x
=−
GM
L
ln
2d + L
2d − L
5.13 The linear speed of an object on the equator
v = ωR = (7.27 × 10
−5
)(6.4 × 10
6
) = 465.3m/s
The orbital velocity of a surface satellite is
v
0
=
√
gr =
9.8 × 6.4 × 10
6
= 7920 m/s
When launched in the westerly direction the launching speed v
0
will be added
to v as the earth rotates from west to east, while in the easterly direction it will
be subtracted.
westerly launching speed
easterly launching speed
=
7920 + 465
7920 − 465
= 1.125
or 11%.
5.14 Consider an element of arc of length ds = R dθ ,Fig.5.12. The corresponding
mass element dm = λds = λR dθ .
The intensity at the origin where λ is the linear density (mass per unit
length) due to dm will be
GλR dθ
R
2
or
Gλ dθ
R
The x-component of intensity at the origin due to dm will be
dE
x
=
Gλ
R
dθ sin θ

5.3 Solutions 209
Fig. 5.12
Therefore, the x-component of intensity due to the quarter of circle at the
origin will be
E
x
=
Gλ
R
π/2
0
sin θ dθ =
Gλ
R
Similarly, the y-component of intensity due to the quarter of circle at the origin
will be
E
y
=
Gλ
R
π/2
0
cos θ dθ =
Gλ
R
∴ E =
E
2
x
+ E
2
y
=
√
2
Gλ
R
5.15
g
B
=
F
B
M
=
Gm M
d
2
M
=
Gm
d
2
g
C
=
F
c
M
=
Gm M
(d + R)
2
M
=
Gm
(d + R)
2
g = g
B
− g
C
=
Gm
d
2
−
Gm
(d + R)
2
=
Gm(2Rd + R
2
)
d
2
(d + R)
2
Since d >> R, g ≈
2GmR
d
3
5.16 By problem (5.6) the gravitational energy is given by
U =−
3
5
GM
2
R
(1)
The volume of the star

210 5 Gravitation
V =
4π R
3
3
(2)
∴ R =
3V
4π
1/3
(3)
∴ U =−
3
5
4π
3V
1/3
GM
2
(4)
P =−
∂U
∂V
=−
1
5
4π
3
GM
2
V
4/3
∴ P ∝ V
−4/3
5.17 Consider a line element dx at A distance x from O, Fig. 5.13. The field point
P is at a distance R from the infinite line. Let PA = r.Thex-component of
gravitational field at P due to this line element will get cancelled by a sym-
metric line element on the other side. However, the y-component will add up.
If λ is the linear mass density, the corresponding mass element is λdx
dE = dE
y
=−
Gλdx sin θ
r
2
(1)
Now, r
2
= x
2
+ R
2
(2)
x = R cot θ (3)
∴ r
2
= R
2
cosec
2
θ (4)
dx = R cosec
2
θd θ (5)
Using (4) and (5) in (1)
dE =−
Gλ
R
sin θ dθ
Fig. 5.13

5.3 Solutions 211
Integrating from 0 to π/2 for the contribution from the line elements on the
left-hand side of O and doubling the result for taking into account contribu-
tions on the right-hand side
E =−
2λ
R
π/2
0
sin θ dθ =−
2Gλ
R
5.18 Let the neutral point be located at distance x from the earth’s centre on the
line joining the centres of the earth and moon. If M
e
and M
m
are the masses
of the earth and the moon, respectively, and m the mass of the body placed
at the neutral point, then the force exerted by M
e
and M
m
must be equal and
opposite to that of M
m
on m.
GM
e
m
x
2
=
GM
m
m
(d − x)
2
∴
M
e
M
m
= 81 =
x
2
(d − x)
2
Since d > x, there is only one solution
x
d − x
=+9
or x =
9
10
d
5.19 For a homogeneous sphere of mass M the potential for r ≤ R is given by
V (r) =−
1
2
GM
R
3 −
r
2
R
2
. At the centre of the sphere V (0) =−
3
2
GM
R
.
For a hemisphere at the centre of the base V (0) =−
3
4
GM
R
. The work done
to move a particle of mass m to infinity will be
3
4
GMm
R
.
5.20 Let the point P be at distance r from the centre of the shell such that
a < r < b. The gravitational field at P will be effective only from matter
within the sphere of radius r. The mass within the shell of radii a and r is
4π
3
(r
3
− a
3
)ρ. Assume that this mass is concentrated at the centre. Then the
gravitational field at a point distance r from the centre will be
g(r) =−
4π
3
(r
3
− a
3
)
r
2
ρG
But ρ =
3M
4π(b
3
− a
3
)
212 5 Gravitation
∴ g(r) =−
GM(r
3
− a
3
)
r
2
(b
3
− a
3
)
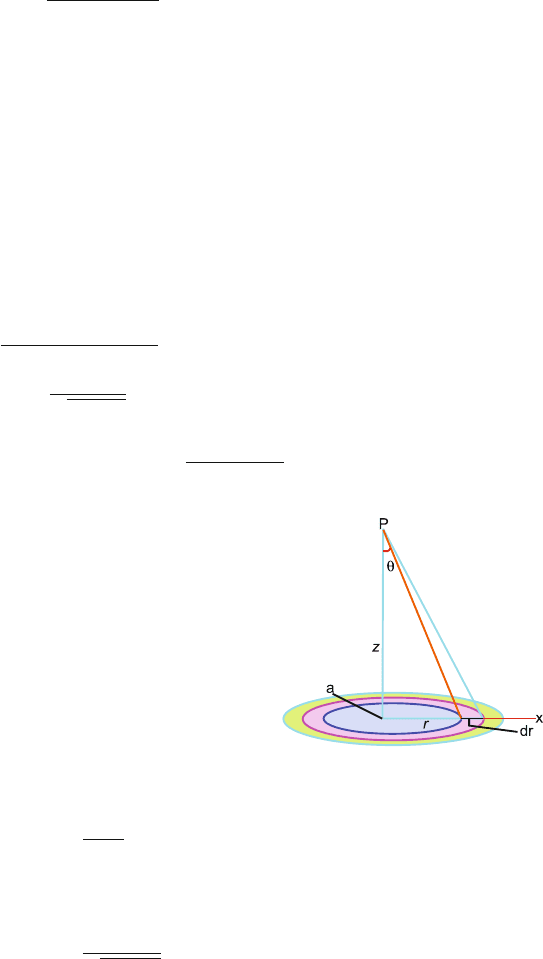
5.21 Let the disc be located in the xy-plane with its centre at the origin. P is a point
on the z-axis at distance z from the origin. Consider a ring of radii r and r +dr
concentric with the disc, Fig. 5.14. The mass of the ring will be
dm = 2πrdrσ (1)
The horizontal component of the field at P will be zero because f or each point
on the ring there will be another point symmetrically located on the ring which
will produce an opposite effect. The vertical component of the field at P will
be
dg
z
=−
G ×2πr dr σ cos θ
(r
2
+ z
2
)
(2)
But cos θ =
z
√
r
2
+ z
2
(3)
g = g
z
=
dg
z
=−2πσG
a
0
zr dr
(r
2
+ z
2
)
3/2
(4)
Fig. 5.14
Put r = z tan θ ,dr = z sec
2
θd θ
g =−2π G =
z/
√
a
2
+z
2
0
sin θ dθ
=−2πσG
1 −
z
√
z
2
+ a
2
5.22 Initially the particle is located at a distance 2R from the centre of the spherical
shell and is at rest. Its potential energy is −GMm/2R. When the particle

5.3 Solutions 213
arrives at the opening the potential energy will be −GMm/R and kinetic
energy
1
2
mv
2
.
Kinetic energy gained = potential energy lost
1
2
mv
2
=−
GMm
2R
−
−
GMm
R
=
1
2
GMm
R
∴ v =
GM
R
After passing through the opening the particle traverses a force-free region
inside the shell. Thus, within the shell its velocity remains unaltered. There-
fore, it hits the point C with velocity v =
GM
R
.
5.3.2 Rockets and Satellites
5.23 Energy conservation gives
1
2
mv
2
−
Gm M
R
=−
Gm M
r
+ 0
where r is the distance from the earth’s centre.
Using v =
GM
2R
, we find r =
4
3
R
Maximum height attained
h = r − R =
R
3
5.24 In Fig. 5.15, total energy at P = total energy at O.
Fig. 5.15

214 5 Gravitation
−
Gm M
√
2R
=
1
2
mv
2
−
Gm M
R
∴ v =
(2 −
√
2)
GM
R
5.25 The potential energy of the satellite on the earth’s surface is
U(R) =−
GMm
R
(1)
where M and m are the mass of the earth and the satellite, respectively, and R
is the earth’s radius.
The potential energy at a height h = 0.5R above the earth’s surface will be
U(R + h) =−
GMm
R + h
=−
GMm
1.5R
(2)
Gain in potential energy
U =−
GMm
1.5R
−
−
GMm
R
=
GMm
3R
(3)
Thus the work done W
1
in taking the satellite from the earth’s surface to a
height h = 0.5 r
W
1
=
GMm
3R
(4)
Extra work W
2
required to put the satellite in the orbit at an attitude h = 0.5R
is equal to the extra energy that must be supplied:
W
2
=
1
2
mv
0
=
1
2
m
GM
R + h
=
GMm
3R
(5)
where v
0
is the satellite’s orbital velocity.
Thus from (4) and (5),
W
1
W
2
= 1.0.
5.26 The initial angular momentum of the asteroid about the centre of the planet is
L = mv
0
d.
At the turning point the velocity v of the asteroid will be perpendicular to
the radial vector. Therefore the angular momentum L
= mv R if the asteroid
is to just graze the planet. Conservation of angular momentum requires that
L
= L. Therefore
5.3 Solutions 215
mv R = mv
0
d (1)
or v =
v
0
d
R
(2)
Energy conservation requires
1
2
mv
2
0
=
1
2
mv
2
−
GMm
R
(3)
or v
2
= v
2
0
+
2GM
R
(4)
Eliminating v between (2) and (4) the minimum value of v
0
is obtained.
v
0
=
2GMR
d
2
− R
2
5.27 According to Kepler’s third law
T
2
∝ r
3
(i)
T
2
E
r
3
E
=
(365.3)
2
(1.5 × 10
11
)
3
= 3.9539 ×10
−29
days
2
/m
3
T
2
v
r
2
v
=
(224.7)
2
(1.08 × 10
11
)
3
= 4.0081 ×10
−29
days
2
/m
3
Thus Kepler’s third law is verified
(ii)
T = 2π
r
3
GM
(1)
where M is the mass of the parent body.
M =
4π
2
G
r
3
T
2
(2)
From (i) the mean value,
%
T
2
r
3
&
= 3.981 × 10
−29
days
2
/m
3
= 2.972 ×
10
−19
s
2
/m
3
M =
4π
2
6.67 × 10
−11
×
1
2.972 × 10
−19
= 1.99 ×10
30
kg
5.28 At the perihelion (nearest point from the focus) the velocity (v
p
)ismaximum
and at the aphelion (farthest point) the velocity (v
A
) is minimum. At both these

216 5 Gravitation
points the velocity is perpendicular to the radius vector. Since the angular
momentum is constant
mv
A
r
A
= mv
p
r
p
or r
A
=
v
p
r
p
v
A
(1)
where r
A
= r
max
and r
p
= r
min
The eccentricity
ε =
r
max
−r
min
r
max
+r
min
=
r
A
−r
p
r
A
+r
p
=
v
p
− v
A
v
p
+ v
A
(2)
where we have used (1)
ε =
30.0 − 29.2
30.0 + 29.2
= 0.0135
A small value of eccentricity indicates that the orbit is very nearly circular.
5.29
(a) For circular orbit,
T =
2πa
v
T = 14.4 days = 1.244 × 10
6
s
2a =
vT
π
=
2.2 × 10
5
× 1.244 × 10
6
3.1416
= 8.7 ×10
10
m
(b) Since the velocity of each component is the same, the masses of the com-
ponents are identical.
v
2
=
G(M +m)
a
=
2GM
a
(∵ m = M)
∴ M =
av
2
2G
=
(4.35 × 10
10
)(2.2 × 10
5
)
2
2 × 6.67 × 10
−11
= 1.58 ×10
31
kg
5.30 At the s urface, the component of velocity of the satellite perpendicular to the
radius R is
v
0
sin 30
◦
=
v
0
2
(Fig. 5.16)
Therefore, the angular momentum at the surface =
mv
0
R
2
