Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.

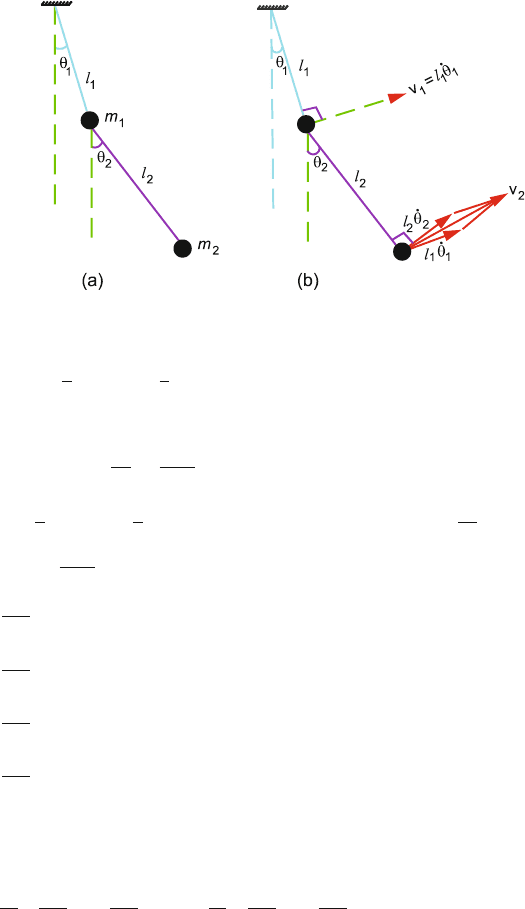
308 7 Lagrangian and Hamiltonian Mechanics
Fig. 7.19
T
1
2
m
1
l
2
1
˙
θ
2
1
+
1
2
m
2
l
2
1
˙
θ
2
1
+l
2
2
˙
θ
2
2
+ 2l
1
l
2
˙
θ
1
˙
θ
2
(4)
V = m
1
gl
1
(1 − cos θ
1
) + m
2
gl
1
(1 − cos θ
1
) + m
2
gl
2
(1 − cos θ
2
)
m
1
gl
1
θ
2
1
2
+
m
2
g
2
l
1
θ
2
1
+l
2
θ
2
2
(5)
L =
1
2
m
1
l
2
1
˙
θ
2
1
+
1
2
m
2
l
2
1
˙
θ
2
1
+l
2
2
˙
θ
2
2
+ 2l
1
l
2
˙
θ
1
˙
θ
2
− m
1
gl
1
θ
2
1
2
−
m
2
g
2
l
1
θ
2
1
+l
2
θ
2
2
(6)
∂ L
∂
˙
θ
1
= m
1
l
2
1
˙
θ
1
+ m
2
l
2
1
˙
θ
1
+ m
2
l
1
l
2
˙
θ
2
(7)
∂ L
∂θ
1
=−m
1
gl
1
θ
1
− m
2
gl
1
θ
1
=−(m
1
+ m
2
)gl
1
θ
1
(8)
∂ L
∂
˙
θ
2
= m
2
l
2
2
˙
θ
2
+ m
2
l
1
l
2
˙
θ
1
(9)
∂ L
∂θ
2
=−m
2
gl
2
θ
2
(10)
Lagrange’s equations are
d
dt
∂ L
∂
˙
θ
1
−
∂ L
∂θ
1
= 0,
d
dt
∂ L
∂
˙
θ
2
−
∂ L
∂θ
2
= 0, (11)
using (7, (8), (9) and 10) in (11) we obtain the equations of motion
(m
1
+ m
2
)l
1
¨
θ
1
+ m
2
l
2
¨
θ
2
+ (m
1
+ m
2
)gθ
1
= 0 (12)
l
2
¨
θ
2
+ gθ
2
+l
1
¨
θ
1
= 0 (13)
7.3 Solutions 309
7.13 Writing p
θ
and p
φ
for the generalized momenta, by (4) and (5) and V by (1)
of prob. (7.10)
∂ L
∂
˙
θ
= P
θ
= ml
2
˙
θ,
˙
θ =
P
θ
ml
2
(1)
∂ L
∂
˙
φ
= p
φ
= ml
2
sin
2
θ
˙
φ,
˙
φ =
p
φ
ml
2
sin
2
θ
(2)
H = ˙q
i
∂ L
∂ ˙q
i
− L or H + L = 2T = ˙q
i
∂ L
∂ ˙q
i
2T =
˙
θ
∂ L
∂
˙
θ
+
˙
φ
∂ L
∂
˙
φ
=
1
ml
2
p
2
θ
+ cosec
2
θ p
2
φ
(3)
∴ H = T + V =
1
2ml
2
p
2
θ
+ cos ec
2
θ p
2
φ
− mgl cos θ (4)
The coordinate φ is ignorable, and therefore p
φ
is a constant of motion deter-
mined by the initial conditions. We are then left with only two canonical equa-
tions to be solved. The canonical equations are
˙q
j
=
∂ H
∂p
j
, ˙p
j
=−
∂ H
∂q
j
˙
θ =
∂ H
∂p
θ
=
p
θ
ml
2
(5)
˙p
θ
=−
∂ H
∂θ
=
p
2
φ
ml
2
cos θ
sin
3
θ
− mgl sin θ (6)
where p
φ
is a constant of motion. By eliminating p
θ
we can immediately
obtain a second-order differential equation in θ as in prob. (7.10).
7.14
H =
1
2
p
2
+
1
2
ω
2
q
2
(1)
∂ H
∂p
=˙q = p (2)
∂ H
∂q
=−˙p = ω
2
q (3)
Differentiating (2)
¨q =˙p =−ω
2
q (4)
Let q = x, then (4) can be written as
¨x +ω
2
x = 0(5)

310 7 Lagrangian and Hamiltonian Mechanics
This is the equation for one-dimensional harmonic oscillator. The general
solution is
x = A sin(ωt + ε) + B cos(ωt + ε) (6)
which can be verified by substituting (6) in (5). Here A, B and ε are constants
to be determined from initial conditions.
7.15 Let r, θ be the instantaneous polar coordinates of a planet of mass m revolving
around a parent body of mass M:
T =
1
2
m( ˙r
2
+r
2
˙
θ
2
) (1)
V = GMm
1
2a
−
1
r
(2)
where G is the gravitational constant and 2a is the major axis of the ellipse:
p
r
=
∂T
∂ ˙r
= m ˙r, ˙r =
p
r
m
(3)
p
θ
=
∂T
∂
˙
θ
= mr
2
˙
θ,
˙
θ =
p
θ
mr
2
(4)
H =
1
2m
p
2
r
+
p
2
θ
r
2
+ GMm
1
2a
−
1
r
(5)
and the Hamiltonian equations are
∂ H
∂p
r
=
p
r
m
=˙r,
∂ H
∂r
=−
p
2
θ
mr
3
+
GMm
r
2
=−˙p
r
(6)
∂ H
∂p
θ
=
p
θ
mr
2
,
∂ H
∂θ
= 0 =−˙p
θ
(7)
Two equations in (7) show that
p
θ
= constant = mr
2
˙
θ (8)
meaning the constancy of angular momentum or equivalently the constancy
of areal velocity of the planet (Kepler’s second law of planetary motion).
Two equations in (6) yield
¨r =
˙p
r
m
=
p
2
θ
m
2
r
3
−
GMm
r
2
= r
˙
θ
2
−
GMm
r
2
(9)
7.3 Solutions 311
Equation (9) describes the orbit of the planet (Kepler’s first law of planetary
motion)
7.16
T =
1
2
m
1
˙x
2
1
+
1
2
m
2
˙x
2
2
(1)
V =
1
2
k(x
1
− x
2
)
2
(2)
L =
1
2
m
1
˙x
2
1
+
1
2
m
2
˙x
2
2
−
1
2
k(x
1
− x
2
)
2
(3)
Equations of motion are
d
dt
∂ L
∂ ˙x
1
−
∂ L
∂x
1
= 0(4)
d
dt
∂ L
∂ ˙x
2
−
∂ L
∂x
2
= 0(5)
Using (3) in (4) and (5)
m
1
¨x
1
+ k(x
1
− x
2
) = 0(6)
m
2
¨x
2
− k(x
1
− x
2
) = 0(7)
It is assumed that the motion is periodic and can be considered as superposi-
tion of harmonic components of various amplitudes and frequencies. Let one
of these harmonics be represented by
x
1
= A sin ωt, ¨x
1
=−ω
2
A sin ωt (8)
x
2
= B sin ωt, ¨x
2
=−ω
2
B sin ωt (9)
Substituting (8) and (9) in (6) and (7) we obtain
(k −m
1
ω
2
) A − kB = 0
− kA+(k − m
2
ω
2
)B = 0
The frequency equation is obtained by equating to zero the determinant
formed by the coefficients of A and B:
(k −m
1
ω
2
) −k
−k (k − m
2
ω
2
)
= 0
Expansion of the determinant gives
m
1
m
2
ω
4
− k(m
1
+ m
2
)ω
2
= 0
312 7 Lagrangian and Hamiltonian Mechanics
or
ω
2
[m
1
m
2
ω
2
− k(m
1
+ m
2
)]=0
which yields the natural frequencies of the system:
ω
1
= 0 and ω
2
=
k(m
1
+ m
2
)
m
1
m
2
=
k
μ
where μ is the reduced mass. The frequency ω
1
= 0 implies that there is no
genuine oscillation of the block but mere translatory motion. The second fre-
quency ω
2
is what one expects for a simple harmonic oscillator with a reduced
mass μ.
7.17 Let x(t) be the displacement of the block and θ(t) the angle through which
the pendulum swings. The kinetic energy of the system comes from the
motion of the block and the swing of the bob of the pendulum. The potential
energy comes from the deformation of the spring and the position of the bob,
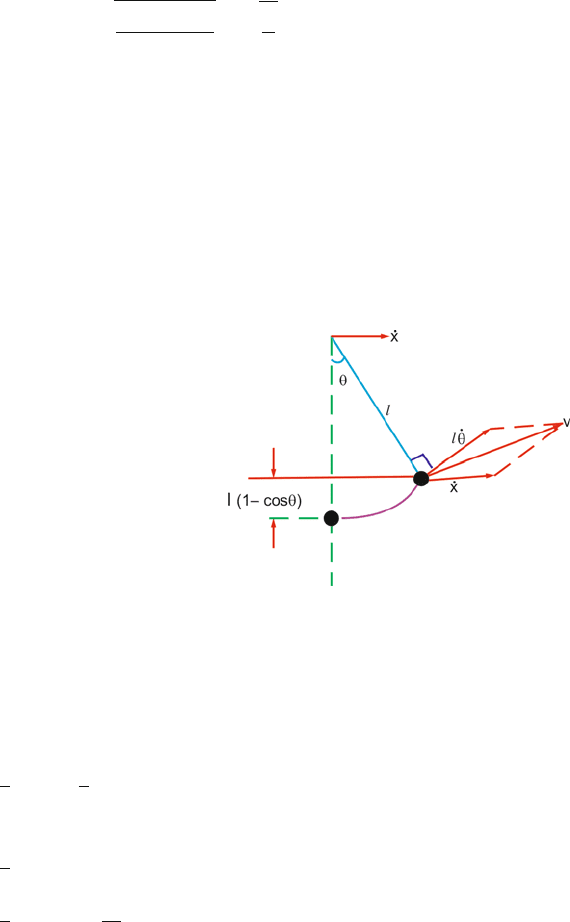
Fig. 7.20.
Fig. 7.20
The velocity v of the bob is obtained by combining vectorially its linear
velocity (l
˙
θ) with the velocity of the block ( ˙x). The height through which the
bob is raised from the equilibrium position is l(1−cos θ), where l is the length
of the pendulum:
v
2
=˙x
2
+l
2
˙
θ
2
+ 2l ˙x
˙
θ cos θ (1)
T =
1
2
M ˙x
2
+
1
2
m( ˙x
2
+l
2
˙
θ
2
+ 2l ˙x
˙
θ) (2)
(∵ for θ → 0, cos θ → 1)
V =
1
2
kx
2
+ mgl (1 −cos θ)
=
1
2
kx
2
+ mgl
θ
2
2
(3)

7.3 Solutions 313
L =
1
2
M ˙x
2
+
1
2
m( ˙x
2
+l
2
˙
θ
2
+ 2l ˙x
˙
θ) −
1
2
kx
2
− mgl
θ
2
2
(4)
Applying Lagrange’s equations
d
dt
∂ L
∂ ˙x
−
∂ L
∂x
= 0,
d
dt
∂ L
∂
˙
θ
−
∂ L
∂θ
= 0(5)
we obtain
(M + m) ¨x + ml
¨
θ +kx = 0(6)
l
¨
θ +¨x + gθ = 0(7)
7.18 Considering that at t = 0 the insect was in the middle of the rod, the coordi-
nates of the insect x, y, z at time t are given by
x = (a +vt) sin θ cos φ
y = (a + vt) sin θ sin φ
z = (a + vt) cos θ
and the square of its velocity is
˙x
2
+˙y
2
+˙z
2
= v
2
+ (a + vt)
2
(
˙
θ
2
+
˙
φ
2
sin
2
θ)
∴ T =
2
3
Ma
2
(
˙
θ
2
+
˙
φ
2
sin
2
θ) +
m
2
{v
2
+ (a + vt)
2
(
˙
θ
2
+
˙
φ
2
sin
2
θ)}
V =−Mga cos θ −mg(a +vt) cos θ +constant
L = T − V
The application of the Lagrangian equations to the coordinates θ and φ yields
d
dt
4
3
Ma
2
˙
θ +m(a +vt)
2
˙
θ
−
4
3
Ma
2
+ m(a + vt)
2
˙
φ
2
sin θ cos θ
=−{Ma + m(a +vt)}g sin θ (1)
and
d
dt
4
5
Ma
2
+ m(a + vt)
2
˙
φ sin
2
θ
= 0(2)
Equation (2) can be integrated at once as it is free from φ:
4
5
Ma
2
+ m(a + vt)
2
˙
φ sin
2
θ = constant = C (3)

314 7 Lagrangian and Hamiltonian Mechanics
Equation (3) is the equation for the constancy of angular momentum about the
vertical axis.
When
˙
φ in (2) is eliminated with the aid of (3) we obtain a second-order
differential equation in θ.
7.19 Let ρ be the linear density of the rod, i.e. mass per unit length. Consider an
infinitesimal element of length of the rod
Fig. 7.21
dT = ρω
2
(l sin θ + x sin φ)
2
dx
T =
dT = ρω
2
2a
0
(l
2
sin
2
θ +2lx sin θ sin φ + x
2
sin
2
φ)dx
= ω
2
Ml
2
sin
2
θ +2Mla sin θ sin φ +
4
3
Ma
2
sin
2
φ
(1)
where we have substituted ρ = M/2a:
V =−Mg(l cos θ + a cos φ) (2)
L = ω
2
Ml
2
sin
2
θ +2Mla sin θ sin φ +
4
3
Ma
2
sin
2
φ
+ Mg(l cos θ + a cos φ) (3)
∂ L
∂
˙
θ
= 0,
∂ L
∂θ
= ω
2
(2Ml
2
sin θ cos θ + 2Mla cos θ sin φ) − Mgl sin θ (4)
∂ L
∂
˙
φ
= 0,
∂ L
∂φ
= ω
2
2Mla sin θ cos φ +
8
3
Ma
2
sin φ cos φ
−Mgasin φ (5)
The Lagrange’s equations
d
dt
∂ L
∂
˙
θ
−
∂ L
∂θ
= 0,
d
dt
∂ L
∂
˙
φ
−
∂ L
∂φ
= 0(6)
7.3 Solutions 315
yield
2ω
2
(l sin θ + a sin φ) = g tan θ (7)
2ω
2
(l sin θ +
4
3
a sin φ) = g tan φ (8)
Equation (7) and (8) can be solved to obtain θ and φ.
7.20 Express the Cartesian coordinates in terms of plane polar coordinates (r, θ)
x = r cos θ, y = r sin θ (1)
˙x =˙r cos θ −r
˙
θ sin θ (2)
˙y =˙r sin θ +r
˙
θ cos θ (3)
Square (2) and (3) and add
v
2
=˙x
2
+˙y
2
=˙r
2
+r
2
˙
θ
2
(4)
T =
1
2
mv
2
=
1
2
m( ˙r
2
+r
2
˙
θ
2
) (5)
V = U(r) (6)
∴ L = T − V =
1
2
m( ˙r
2
+r
2
˙
θ
2
) −U(r)(Lagrangian) (7)
Generalized momenta:
p
k
=
∂ L
∂ ˙q
k
, p
r
=
∂ L
∂ ˙r
= m ˙r, p
θ
=
∂ L
∂
˙
θ
= mr
2
˙
θ (8)
Hamiltonian:
H = T + V =
1
2
m( ˙r
2
+r
2
˙
θ
2
) + V (r) (9)
Conservation of Energy: In general H may contain an explicit time depen-
dence as in some forced systems. We shall therefore write H = H(q, p, t).
Then H varies with time for two reasons: first, because of its explicit depen-
dence on t, second because the variable q and p are themselves functions of
time. Then the total time derivative of H is
dH
dt
=
∂ H
∂t
+
n
β=1
∂ H
∂q
β
˙q
β
+
n
β=1
∂ H
∂p
β
˙p
β
(10)

316 7 Lagrangian and Hamiltonian Mechanics
Now Hamilton’s equations are
∂ H
∂p
β
=˙q
β
,
∂ H
∂q
β
=−˙p
β
(11)
Using (11) in (10), we obtain
dH
dt
=
∂ H
∂t
+
n
β=1
∂ H
∂q
β
∂ H
∂p
β
−
∂ H
∂p
β
∂ H
∂q
β
(12)
whence
dH
dt
=
∂ H
∂t
(13)
Equation (13) asserts that H changes with time only by virtue of its explicit
time dependence. The net change is induced by the fact that the variation of q
and p with time is zero.
Now in a conservative system, neither T nor V contains any explicit depen-
dence on time.
Hence
∂ H
∂t
= 0. It follows that
dH
dt
= 0 (14)
which leads to the law of conservation of energy
H = T + V = E = constant (15)
The Hamiltonian formalism is amenable for finding various conservation
laws.
Conservation of angular momentum: The Hamiltonian can be written as
H =
n
β=1
p
β
˙q
β
− L (16)
Using the polar coordinates (r, θ)
H = p
r
˙r + p
θ
˙
θ −
1
2
m ˙r
2
+
1
2
mr
2
˙
θ
2
−U(r)
(17)
Using (7) and (8) in (17)

7.3 Solutions 317
H =
p
2
r
2m
+
p
2
θ
2mr
2
+U(r) (18)
Now the second equation in (11) gives
−˙p
θ
=
∂ H
∂θ
= 0 (∵ θ is absent in(18)) (19)
This leads to the conservation of angular momentum
p
θ
= J = constant (20)
7.21 Let each mass be m.
(a)
T =
1
2
m ˙x
2
+
1
2
m ˙y
2
=
1
2
m( ˙x
2
+˙y
2
) (1)
V =
1
2
kx
2
+
1
2
3k(x − y)
2
+
1
2
ky
2
= k(2x
2
− 3xy + 2y
2
) (2)
L = T − V =
1
2
m( ˙x
2
+˙y
2
) − k(2x
2
− 3xy + 2y
2
) (3)
(b)
d
dt
∂ L
∂ ˙x
−
∂ L
∂x
= 0(4)
and
d
dt
∂ L
∂ ˙y
−
∂ L
∂y
= 0(5)
yield
m ¨x =−4kx + 3ky (6)
m ¨y = 3kx − 4ky (7)
(c)
Let x = A sin ωt and y = B sin ωt(8)
¨x =−Aω
2
sin ωt and ¨y =−Bω
2
sin ωt(9)
Substituting (8) and (9) in (6) and (7) and simplifying we obtain
(4k −ω
2
m) A − 3kB = 0 (10)
− 3kA+(4k − ω
2
m)B = 0 (11)
The frequency equation is obtained by equating to zero the determinant
formed by the coefficients of A and B:
(4k −ω
2
m) −3k
−3k (4k −ω
2
m)
= 0 (12)
