Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.

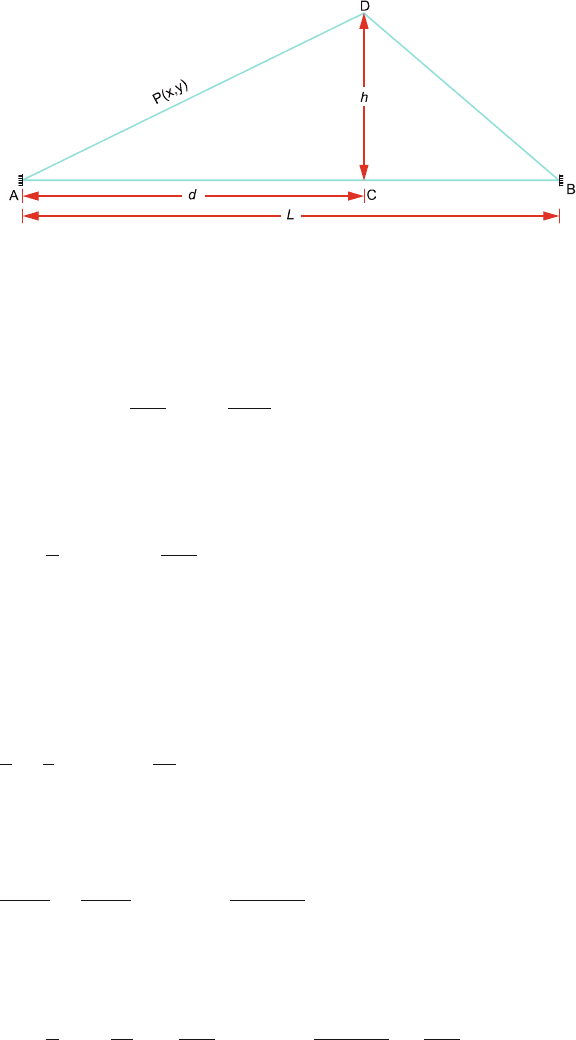
358 8Waves
P′(x,y)
Fig. 8.4
The general form of the displacement at any point x and time t is given by the
Fourier expansion
y =
∞
n=1
a
n
sin
nπ x
L
cos
nπvt
L
(1)
The coefficient a
n
is obtained from
a
n
=
2
L
L
0
y
0
sin
nπ x
L
dx (2)
where y
0
= y(x, 0).
We break the integral into two parts, one from 0 to d and the other from d to L.
In the interval from 0 to d the equation of the initial configuration of the string
for a typical point p(x, y) is
y
x
=
h
d
or y =
hx
d
for o < x < d
and in the interval d to L, the equation for P
(x, y) is
y
L − x
=
h
L − d
or y =
h(L − x)
L − d
for d < x < L
so that by substituting (1) into (2) with t = 0
a
n
=
2
L
d
0
hx
d
sin
πnx
L
dx +
L
d
h(L − x)
L − d
sin
πnx
L
dx
(3)

8.3 Solutions 359
Integrating by parts
a
n
=
2hL
2
n
2
π
2
d(L − d)
sin
nπd
L
(4)
Here d =
1
2
L, so that (4) becomes
a
n
=
8h
n
2
π
2
sin
nπ
2
If n is an even integer then the corresponding a
n
is zero. If n is an odd integer,
then the sine term alternates in sign as sin
π
2
= 1, sin
3π
2
=−1, sin
5π
2
= 1 ...,
so that we may write
a
n
=
8h
π
2
n
2
(−1)
(n−1)/2
(5)
Using (5) in (1)
y =
8h
π
2
sin
π x
L
cos
πvt
L
−
1
9
sin
3π x
L
cos
3πvt
L
+
1
25
sin
5π x
L
cos
5πvt
L
−
1
49
sin
7π x
L
cos
7πvt
L
+···
Note that the even harmonics are absent. Since the intensity of a wave is pro-
portional to the square of its amplitude, then for the sound emitted by the string,
the fundamental would have an intensity of 81 times the third harmonic and 625
times the fifth harmonic, etc.
Formula (4) shows that the nth harmonic will be absent if sin
nπd
L
=
0. a
n
= 0ifd = L/n,2L/n,3L/n, i.e. nd/L is any integer or whenever
there is any node of the nth harmonic situated at D, Fig. 8.4. If the string is
divided into n equal parts and is plucked at any dividing point, the nth harmonic
will disappear from the resultant vibration. In particular, any force applied at
the midpoint of the string cannot produce even harmonics. Further after the
application of force at the midpoint of the string, if this point be lightly touched
the string ceases to vibrate. This is because odd harmonics cannot be sustained
with a node at the midpoint, and the even harmonics are already absent for
reasons discussed above.
8.4
y = y
1
+ y
2
= A sin(kx − ωt) + 3A sin(kx +ωt)
=[A sin(kx −ωt) + A sin(kx +ωt)]+2A sin(kx +ωt)
= 2A sin kx cos ωt + 2A sin(kx +ωt)
where we have used the identity
sin C +sin D = 2sin
C + D
2
cos
C − D
2

360 8Waves
Thus the resultant wave = standing wave + travelling wave in the negative
direction.
The amplitudes are (a) 2A (b) 2A
8.5
(a) The wave number k =
2π
λ
=
2π
2
= π/m
Frequency f =
v
λ
=
8
2
= 4Hz
Angular frequency ω = 2π f = (2π)(4) = 8π rad/s
(b) y = A sin(kx − ωt) = A sin π(x −8t)
8.6 Let y = A sin(kx −ωt + φ)
At x = 0, t = 0, the wave has the maximum displacement and y = A:
A = A sin(0 − 0 +φ)
or sin φ = 1 → φ =
π
2
∴ y = A sin
kx − ωt +
1
2
π
= A cos(kx − ωt)
∴ y = 0.2 cos(3x −20t)
8.7
y = 2A sin kx cos ωt (standing wave)
∂y
∂t
=−2Aω sin kx sin ωt
Acceleration, a =
∂
2
y
∂t
2
=−ω
2
2A sin kx cos ωt =−ω
2
y.
This is the defining equation for the SHM.
8.8
f
N
=
Nv
2L
f
1
=
1 × 120
2 × 2
= 30 Hz
f
2
=
2 × 120
2 × 2
= 60 Hz
f
3
=
3 × 120
2 × 2
= 90 Hz
f
4
=
4 × 120
2 × 2
= 120 Hz
8.3 Solutions 361
8.9
f
1
=
1
2L
1
F
μ
1
f
2
=
1
2L
2
F
μ
2
∴
μ
2
μ
1
=
(L
1
f
1
)
2
(L
2
f
2
)
2
=
(0.05 × 4800)
2
(2.0 × 32)
2
14
8.10
y = 5sinπ(0.02x −4.00t) = 5sin2π(0.01x −2.00t) (given equation) (1)
y = A sin 2π
x
λ
− ft
(standard equation) (2)
Comparing (1) and (2)
A = 5cm, f = 2Hz
1
λ
= 0.01 or λ = 100 cm
v = f λ = 2 × 100 = 200 cm/s
8.11
y = 4sin
1
2
π x cos 20π t (standing wave) (1)
y = 2A sin kx cos ωt (standard equation) (2)
Comparing (1) and (2)
(a) 2A = 4orA = 2cm,k =
π
2
, ω = 20π
v =
ω
k
=
20π
π/2
= 40 cm/s
(b) λ =
2π
k
=
2π
π/2
= 4cm
Distance between nodes =
λ
2
=
4
2
= 2cm
(c)
∂y
∂t
=−(4)(20π)sin
1
2
π x sin 20πt
∂y
∂t
x=1.0, t=9/4
=−80π sin
π
2
sin 45π = 0
8.12 Thewaveisoftheform
y = A sin(kx − ωt + φ)
(a) ω = 2π f = (2π)(250) = 500π rad/s
k =
ω
v
=
500π
375
=
4π
3
m
−1
362 8Waves
φ = 60
◦
=
π
3
rad
x =
φ
k
=
π/3
4π/3
= 0.25 m
(b) φ = ωt = (500π)(10
−3
) =
π
2
rad = 90
◦
8.13
y
1
= A
1
sin(kx − ωt)
y
2
= A
2
sin
kx − ωt +
π
2
= A
2
cos(kx − ωt)
y = y
1
+ y
2
= A
1
sin(kx − ωt) + A
2
cos(kx − ωt)
=
A
2
1
+ A
2
2
⎡
⎣
A
1
A
2
1
+ A
2
2
sin(kx − ωt) +
A
2
A
2
1
+ A
2
2
cos(kx − ωt)
⎤
⎦
Put
A
1
A
2
1
+ A
2
2
= cos α. Then
A
2
A
2
1
+ A
2
2
= sin α
∴ y =
A
2
1
+ A
2
2
[sin(kx − ωt) cos α + cos(kx − ωt) sin α]
=
A
2
1
+ A
2
2
sin(kx − ωt + α)
which has the amplitude A =
A
2
1
+ A
2
2
=
√
6
2
+ 8
2
= 10 cm.
Graphical Method
This method was outlined in prob. (6.50). The waves are represented as vectors, the
magnitudes being proportional to the amplitudes, the orientation according to the
phase difference. Here the vectors OAand AB are laid in the head-to-tail fashion,
Fig. 8.5. The amplitude of the resultant wave is given by OB which is found to be
10 cm from the right angle triangle OAB
Fig. 8.5
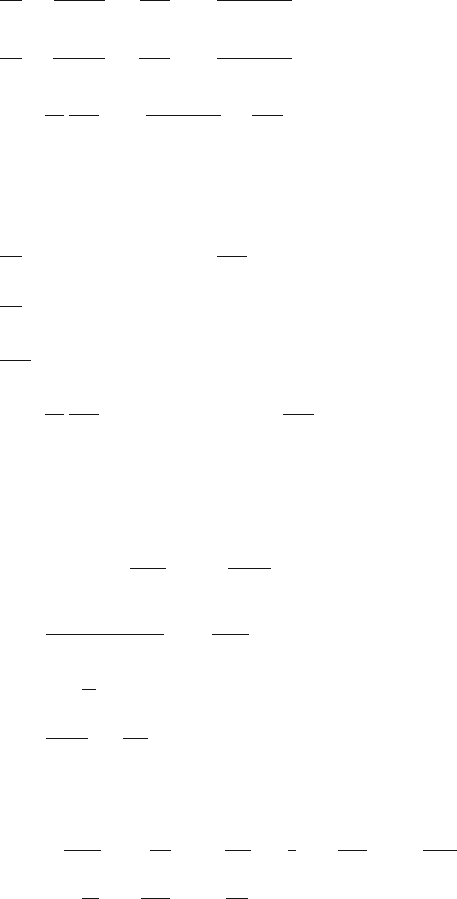
8.3 Solutions 363
8.14
(a) y = A ln(x + vt)
∂y
∂x
=
A
x + vt
,
∂
2
y
∂x
2
=−
A
(x + vt)
2
∂y
∂t
=
Av
x + vt
,
∂
2
y
∂t
2
=−
Av
2
(x + vt)
2
∴
1
v
2
∂
2
y
∂t
2
=−
A
(x + vt)
2
=
∂
2
y
∂x
2
Thus the wave equation is satisfied.
(b) y = A cos(x + vt)
∂y
∂x
=−A sin(x +vt)
∂
2
y
∂x
2
=−A cos(x +vt)
∂y
∂t
=−v A sin(x + vt)
∂
2
y
∂t
2
=−v
2
A cos(x + vt)
∴
1
v
2
∂
2
y
∂t
2
=−A cos(x +vt) =
∂
2
y
∂x
2
Thus the wave equation is satisfied.
8.15 (a) By prob. (8.3)
y =
∞
n=1
a
n
sin
nπ x
L
cos
nπvt
L
(1)
a
n
=
2hL
2
n
2
π
2
d(L − d)
sin
nπd
L
(2)
Here d =
L
3
and (2) becomes
a
n
=
9h
n
2
π
2
sin
nπ
3
(3)
Inserting (3) in (1)
∴ y =
3
5/2
h
2π
2
sin
π x
L
cos
πvt
L
+
1
4
sin
2π x
L
cos
2πvt
L
−
1
16
sin
4π x
L
cos
4vt
L
...
(4)
(b) For n = 3, 6 or 9, the sine term in (3) becomes zero. Therefore, the t hird,
sixth and ninth harmonics will be absent.

364 8Waves
8.16 General equation for a progressive wave in the negative x-direction is
y = A sin(kx + ωt)
ω = 2π f = 2π × 170 = 340π rad/s
k =
ω
v
=
340π
340
= π/m
∴ y = 0.01 sin π(x +340t)
8.17 (a)
y
1
= A sin(kx − ωt)
y
2
= A sin(kx + ωt)
y = y
1
+ y
2
= 2A sin kx cos ωt
where we have used the identity stated in prob. (8.4).
(b) The nodes are formed when kx = nπ or
2π
λ
x = nπ
or x =
nλ
2
x = 0,
λ
2
,λ,...
The antinodes are formed when kx =
nπ
2
or x =
nλ
4
x =
1
4
,
3
4
,
5
4
...
8.18
y
1
= A sin(kx − ωt)
y
2
= A sin(kx − ωt + δ)
y = y
1
+ y
2
= A[sin(kx −ωt) + sin(kx −ωt + δ)]
= 2A cos
1
2
δ sin
kx − ωt +
δ
2
Thus the amplitude of the resultant wave is 2A cos
1
2
δ.
For A = 6 cm and δ =
π
2
, the amplitude of the resultant wave will be 2 ×
6 cos
π
4
or 6
√
2cm.
For 2A cos
1
2
δ = 6
cos
1
2
δ =
6
2A
=
6
2 × 6
=
1
2
= cos
π
3
∴
1
2
δ =
π
3
or δ =
2π
3
8.3 Solutions 365
If two sound waves with slightly different frequencies are produced then beats
are heard. These consist of regular swelling and fading of the sound. In one
set of waves compressions and rarefactions will be spaced further apart, in
another they will be close enough. At some instant, two compressions arrive
together at the ear of the listener and the sound is loud. At a later time, the
compression of one wave arrives with the rarefaction of the other and the
sound will be faint. Beats are thus caused due to interference of sound waves
of neighbouring frequencies in time. The beat frequency is equal to the differ-
ence f
1
∼ f
2
for the two component waves. Beats between two tones can be
detected by the ear up to a frequency of about 7/s.
8.19 Consider an infinitesimal element of length dx of the string of linear mass
density μ. The mass element μdx will execute SHM with amplitude A.The
maximum kinetic energy will be
1
2
(μdx)ω
2
A
2
.
Energy transmitted across the string per second, i.e. power
P =
1
2
μ
dx
dt
ω
2
A
2
=
1
2
μvω
2
A
2
8.20 Let the fork of frequency f be in unison with 99 cm of the string. Then
f =
1
2 × 99
F
μ
(1)
When the length of the string was 100 cm the frequency must have been less
by 4 beats. Thus
f − 4 =
1
2 × 100
F
μ
(2)
Dividing (1) by (2) and solving
f
f − 4
=
100
99
We get f = 400/s.
8.21
y(x, t) =
0.10
(2x − t)
2
+ 4
∴ y(0, 0) =
0.10
4
= 0.025
Let y(x, t) = 0.025 =
0.10
4 + (2x − t)
2

366 8Waves
Solving we find
v =
x
t
= 0.5 m/s along the + x − direction.
Now, y(−x, t) =
0.10
4 + (2x + t)
2
= y(x, t)
Therefore, the pulse is not symmetric.
8.22
(a) f =
N
2l
F
μ
(N = 1)
μ =
F
4 f
2
L
2
=
300
(4)(660)
2
(0.6)
2
= 4.78 ×10
−4
kg/m
(b) The frequencies of the first two harmonics are f
2
= 2 f = 1320 Hz and
f
3
= 3 f = 1980 Hz.
(c) For open pipe length is
L =
λ
2
=
v
2 f
=
340
2 × 660
= 0.2576 m
8.23
(a) First harmonic – second harmonic (Fig. 8.6)
Fig. 8.6
v =
F
μ
,λ=
2L
N
f
N
=
v
λ
N
f
N
=
N
2L
F
μ
, N = 1, 2, 3,...
(b) The standard equation for the standing wave is
y(x, t) = 2A sin kx cos ωt (1)
Given equation is
y(x, t) = 0.024 sin(62.8x) cos(471t) (2)
Comparison shows that
k = 62.8 and ω = 471
8.3 Solutions 367
Wave velocity v =
ω
k
=
471
62.8
= 7.5m/s
λ =
2π
k
=
2π
62.8
= 0.1m
Distance between nodes =
λ
2
=
0.1
2
= 0.05 m
8.24 y = A sin(kx + ωt)
(i) y = 8.2 × 10
−2
sin(22x + 100t)(negative x-direction)
(ii) y = 8.2 × 10
−2
sin(100t − 22x)(positive x-direction)
(iii) λ =
2π
k
=
2π
22
= 0.2856 m
T =
2π
ω
=
2π
100
= 0.0628 m
v =
ω
k
=
100
22
= 4.545 m/s
(iv)
y = 8.2 × 10
−2
× sin(22 × 3.2 + 100 × 2.5)
= 8.2 ×10
−2
× sin(51 × 2π) = 0
8.25
F
μ
1/2
=
MLT
−2
ML
−1
1/2
=
LT
−1
=[v]
8.26 Let the travelling wave be represented by
y = A sin(kx − ωt)
Then
∂y
∂x
= kAcos(kx − ωt) (1)
∂y
∂t
=−ω A cos(kx −ωt)
=−vkAcos(kx − ωt) =−v
∂y
∂x
(2)
Combining (1) and (2),
∂y
∂x
=−
∂y
∂t
/v.
8.27
(a) Let a long string of linear density μ be stretched by a force F. Assume that
the damping is negligible. Take the x-axis in the direction of the undis-
placed string and y-axis in the direction perpendicular to it. If θ is the
angle between the tangent to the string and the x-axis, the tension in the
horizontal direction (x-axis) would be T cos θ and in the vertical direction
(y-axis) it would be T sin θ . Assuming that θ is very small, cos θ 1 and
consequently the x-component of the tension remains constant. We are
therefore concerned only with the y-component of the tension.
