Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.

368 8Waves
Referring to Fig. 8.1 note that the forces across x the element of length
of the string make angles θ
1
and θ
2
with the x-axis. Let θ
2
= θ and θ
1
=
θ +dθ. To find the equation of motion of this element subject to these
forces, the difference in tension acting across x in the y-direction is
dF
y
= F{sin(θ +dθ) − sin θ }
= F{sin θ cos(dθ) + cos θ sin(dθ) − sin θ}
but cos(dθ) 1 and sin(dθ) dθ, since dθ is small :
∴ dF
y
= F cos θ dθ = Fd(sin θ)
In the small angle approximation
sin θ tan θ =
∂y
∂x
this last quantity being the gradient of the curve
∴ dF
y
= F
∂
∂x
∂
∂y
dx = F
∂
2
y
∂x
2
dx (1)
The mass of the element x is μ dx, and its acceleration in the y-direction
is d
2
y/dt
2
. Hence by Newton’s second law of motion
μdx
∂
2
y
∂t
2
= F
∂
2
y
∂x
2
dx
or
∂
2
y
∂x
2
=
μ
F
∂
2
y
∂t
2
(2)
(b) Let y(x − vt) be a solution of (2)
∂y
∂t
(x − vt) = y
(x − vt)
∂
∂t
(x − vt) =−vy
(x − vt)
where y
is another function of (x − vt) defined by y
(x − vt) =
dy(x −vt)
d(x − vt)
.
The second derivative with respect to time gives
∂
2
y(x −vt)
∂t
2
= v
2
y
(x − vt) (3)
where y
(x − vt) is yet another function of (x −vt) defined by
y
(x − vt) =
dy
(x − vt)
d(x − vt)
=
d
2
y
(x − vt)
d(x − vt)
2

8.3 Solutions 369
proceeding along similar lines, differentiation of the function y(x − vt)
with respect to x yields
∂y(x −vt)
∂x
= y
(x − vt)
∂
∂x
(x − vt) = y
(x − vt)
∂
2
y(x −vt)
∂x
2
= f
(x − vt) (4)
where y(x −vt) and y
(x − vt) are the same functions of (x −vt) as in
(3). Substitution of (3) and (4) into (2) shows that y(x −vt) is a solution,
provided we set
v
2
=
F
μ
8.28
(a) The incident wave has the form
y
1
= A
1
sin(ωt −k
1
x) (1)
The reflected wave has the form
y
2
= A
2
sin(ωt +k
1
x) (2)
The transmitted wave has the form
y
3
= A
3
sin(ωt −k
2
x) (3)
The boundary conditions at the boundary (x = 0) are that the displace-
ment and its first derivative be single valued:
y
1
|
x =0
+ y
2
|
x =0
= y
3
|
x =0
A
1
+ A
2
= A
3
(4)
∂y
1
∂x
|
x =0
+
∂y
2
∂x
|
x =0
=
∂y
3
∂x
|
x =0
− k
1
A
1
+ k
1
A
2
=−k
2
A
3
(5)
Solving (4) and (5)
A
2
=
(k
1
− k
2
)A
1
k
1
+ k
2
; A
3
=
2k
1
A
1
k
1
+ k
2
(6)
(b) A
2
is negative when k
2
> k
1
or
ω
v
2
>
ω
v
1
or μ
2
>μ
1
, i.e. wire 2 has
greater linear density than wire 1.
370 8Waves
8.29
5
2
λ = 15 cm
∴ λ = 6cm
f =
v
λ
=
2400
6
= 400 Hz
ω = 2π f = 2512 rad/s
k =
2π
λ
= 1.047/cm
A = 6cm
y = A sin(ωt − kx) = 6sin(2512t −1.047x) cm
8.30
P =
1
2
ω
2
A
2
μv = 2π
2
f
2
A
2
μv
= 2π
2
× (400)
2
(0.06)
2
(2.5 × 10
−4
)(24) = 68.2W
8.31
(a) The amplitude of any point of the plucked string at time t may be
written as
y =
∞
n=1
a
n
cos ω
n
t sin
nπ x
L
+
∞
n=1
b
n
sin ω
n
t sin
nπ x
L
(1)
The kinetic energy of vibration of an element of length of string dx in the
nth mode is given by
dK
n
=
1
2
(μdx)( ˙y)
2
=
1
2
μω
2
n
(−a
n
sin ω
n
t + b
n
cos ω
n
t)
2
sin
2
(k
n
x)dx (2)
where we have used the value of velocity ˙y by differentiating (1) for the
nth mode with respect to t.
The potential energy of an element of string of length dx is
dU
n
=
1
2
ky
2
dx
=
1
2
μω
2
n
(a
n
cos ω
n
t + b
n
sin ω
n
t)
2
sin
2
k
n
x d x (3)
wherewehaveused(1).
Adding (2) and (3), the total energy
dE
n
= dK
n
+ dU
n
=
1
2
μω
2
n
(a
2
n
+ b
2
n
) sin
2
k
n
x d x (4)
8.3 Solutions 371
The total energy of the entire string is obtained by integrating from 0 to L
E
n
=
dE
n
=
1
2
μω
2
n
(a
2
n
+ b
2
n
)
L
0
sin
2
(k
n
x)dx
Now
L
0
sin
2
(k
n
x)dx =
L
0
sin
2
nπ x
L
dx =
L
2
∴ E
n
=
1
4
μLω
2
n
(a
2
n
+ b
2
n
) =
1
4
Mω
2
n
(a
2
n
+ b
2
n
)
where M is the total mass of the string.
(b) For the string plucked at the centre a
n
=
8h
n
2
π
2
(see prob. 8.3). Further
ω
n
= k
n
v =
nπv
L
and b
n
= 0. Thus the energy of vibration
E
n
=
M
4
nπv
L
2
8h
n
2
π
2
2
=
16Mh
2
v
2
n
2
π
2
L
2
∴
E
1
E
3
=
9
1
8.3.2 Waves in Solids
8.32
(a) For the rod clamped at one end and free at the other (fixed–free)
f
n
=
n
4L
γ
ρ
(n = 1, 3, 5,...)
f
1
=
1
4L
γ
ρ
=
1
4 × 0.25
2 × 10
11
7860
= 5044 Hz
(b) (i) For the rod free at both ends (free–free)
f
n
=
n
2L
Y
ρ
(n = 1, 2, 3,...)
(ii) For the rod clamped at the midpoint
f
n
=
n
2L
Y
ρ
(n = 1, 3, 5,...)
(iii) For the bar clamped at both ends (fixed–fixed)
f
n
=
n
2L
Y
ρ
(n = 1, 2, 3,...)

372 8Waves
For the case (a) (bar clamped at one end only) the frequency of the fundamen-
tal is half that of a similar free–free (case (b) (i)) or fixed–fixed (case (b) (iii))
bar and only the odd-numbered harmonic overtones are present. This is to be
expected since the effect of clamping a free–free bar at its centre is to suppress
all its even harmonics.
For case (b) (ii) rod clamped at the midpoint only odd partials are present
similar to case (a) (fixed–free) and differs from case (b) (i) (free–free) where
all the partials are present. However the fundamental has the same frequency
in cases (b) (ii) and (b) (i).
8.33
(a) f =
1
2π
k
m
Now k =
F
x
and Y =
F/A
x/L
=
FL
xA
=
kL
A
∴ f =
1
2π
AY
mL
=
1
2π
1 × 10
−5
× 2 × 10
11
2 × 1.0
= 159 c/s
(b) For the given system
kL tan(kL) =
M
m
Mass of the bar, M = ρ AL = 7800 × 1 × 10
−5
× 1.0 = 0.078 kg. The
frequency condition becomes
kL tan(kL) =
0.078
2.0
= 0.039
The solution to the above equation is
kL = 0.196
∴
ωL
v
= 0.196
or f =
ω
2π
=
1
2π
0.196
L
Y
ρ
=
0.196
2π ×1.0
2 × 10
11
7800
= 158 c/s
Observe that the results of (b) are nearly the same as those for (a), showing
thereby for small values of kL, the mass loaded system approximates that of
a simple harmonic oscillator with the mass fixed at the end.
8.34 The frequency condition for this system is
kL tan(kL) =
M
m
8.3 Solutions 373
Expanding tan (kL)byseries
kL
kL +
(kL)
3
3
+ 2
(kL)
5
15
+···
=
M
m
If kL < 0.2, we may retain only the first term within the brackets:
k
2
L
2
=
M
m
ω
2
L
2
v
2
=
M
m
f =
ω
2π
=
1
2π
v
L
M
m
=
1
2π L
Y
ρ
M
m
But Y =
kL
A
and M = ALρ
∴ f =
1
2π
k
m
8.3.3 Waves in Liquids
8.35
(a) v
2
=
g
k
tanh(kh) =
gλ
2π
tanh
2π
λ
λ
4
=
gλ
2π
tan h
π
2
=
9.8
2π
× 0.917 λ
v = 1.2
√
λ m/s
(b) v =
g
k
=
gλ
2π
= 1.25
√
λ m/s
(c) v =
gh =
gλ
4
=
9.8λ
4
= 1.56
√
λ m/s
8.36 The fractional error introduced by the use of the f ormula v =
√
gh is
√
gh −
g
k
tanh(kh)
g
k
tanh(kh)
= 0.01
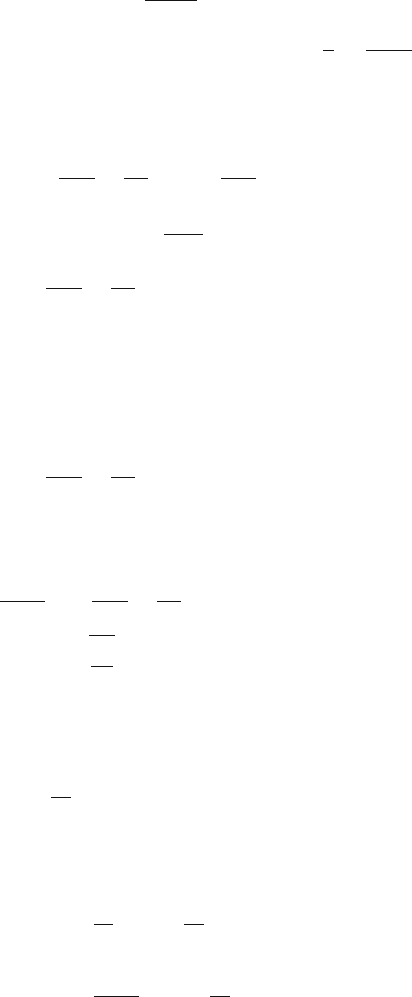
374 8Waves
Put kh = x, then
tanhx
x
= 0.96
This gives the solution x = 0.25 or h =
x
k
=
0.25λ
2π
= 0.04λ.
8.37 Surface conditions are modified by the surface tension S. For the capillary
waves
v
2
=
2π S
ρλ
+
gλ
2π
tanh
2πh
λ
(1)
If h >> λ, tanh
2π h
λ
→ 1, and
v
2
=
2π S
ρλ
+
gλ
2π
(2)
Substituting λ = 0.366 cm, ρ = 1.0g/cm
3
, g = 980 cm/s
2
and v = f λ =
100 × 0.366 = 36.6cm/s in (2) we find S = 74.7 dynes/cm.
8.38 For capillary waves when h >> λ
v
2
=
2π S
ρλ
+
gλ
2π
(1)
The minimum value of the wavelength λ
m
can be found out by minimizing (1):
∂(v
2
)
∂λ
=−
2πS
ρλ
2
m
+
g
2π
= 0
λ
m
= 2π
S
gρ
(2)
Ignoring the second term in the right-hand side of (1) and using (2)
v =
gs
ρ
1/4
For mercury and water
v
1
: v
2
=
S
1
ρ
1
1/4
:
S
2
ρ
2
1/4
=
544
13.56
1/4
:
74
1
1/4
= 0.858 : 1

8.3 Solutions 375
8.39
ω
2
k
2
=
F
μ
+ αk
2
(1)
The phase velocity v
p
=
ω
k
=
F
μ
+ αk
2
=
F
μ
1 +
αμk
2
F
1/2
=
F
μ
1 + α
k
2
μ
2F
+···
(for small α) (2)
Since k = 2π/λ, v
p
increases as λ decreases.
The group velocity is given by
v
g
= v
p
+
k dv
p
dk
= v
p
+ αk
2
μ
F
8.40
(a)
ω =
S
ρ
k
3/2
v
p
=
ω
k
=
S
ρ
√
k
(b)
v
g
= v
p
+
k dv
p
dk
=
S
ρ
√
k +
kS
2ρ
√
k
=
3
2
S
ρ
√
k
(c) From (a) and (b) v
g
>v
p
8.41
(a)
ω
2
=
gk +
S
ρ
k
3
tanh(kh) (1)
If kh << 1, then tanh (kh) = kh and (1) becomes
ω
2
=
gk +
S
ρ
k
3
kh (2)
If the second term in the brackets is smaller than the first one
S
ρ
k
2
<< g
ω
2
= ghk
2
∴ ω = k
gh (3)
v
p
=
ω
k
=
gh (4)
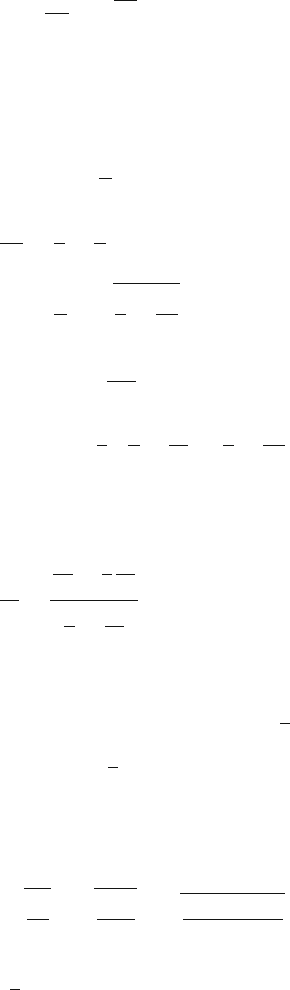
376 8Waves
v
g
=
dω
dk
=
gh (5)
∴ v
g
= v
p
(b) kh >> 1, tanh(kh) = 1 and (1) becomes
ω
2
= gk +
S
ρ
k
3
ω
2
k
2
=
g
k
+
S
ρ
k
v
p
=
ω
k
=
g
k
+
Sk
ρ
(6)
v
g
= v
p
+ k
dv
p
dk
= v
p
+
k
2
S
ρ
−
g
k
2
g
k
+
Sk
ρ
−1/2
Using (6)
v
g
v
p
=
g
2k
+
3
2
ks
ρ
g
k
+
ks
ρ
(7)
For short wavelengths k is larger, the first term in both the numerator and
denominator will be smaller and v
g
=
3
2
v
p
, while for long wavelengths, k is
smaller and v
g
=
1
2
v
p
.
8.42 With reference to prob. (8.41) for small ripples, λ is small and k is large so
that the second term in (6) dominates over the first term in the radical.
v
p
=
Sk
ρ
=
2π S
λρ
=
2π ×0.075
0.01 × 1000
= 0.217 m/s
v
g
=
3
2
v
p
= 0.325 m/s

8.3 Solutions 377
For large waves, first term in (6) is important:
v
p
=
g
k
=
gλ
2π
=
9.8 × 1.0
2π
= 1.25 m/s
v
g
=
1
2
v
p
= 0.625 m/s
8.43 E
2
= c
2
p
2
+ m
2
c
4
¯
h
2
ω
2
= c
2
¯
h
2
k
2
+ m
2
c
4
∴ ω =
c
2
k
2
+
m
2
c
4
¯
h
2
v
p
=
ω
k
=
c
2
+
m
2
c
4
¯
h
2
k
2
v
g
=
dω
dk
=
c
2
k
c
2
k
2
+
m
2
c
4
¯
h
2
=
c
2
c
2
+
m
2
c
4
¯
h
2
k
2
∴ v
p
v
g
= c
2
8.44
v
p
=
gλ
2π
+
2πS
ρλ
(1)
Substituting v
p
= 30 cm/s, g = 980 cm/s
2
, S = 75 dynes/cm and ρ =
1g/cm
3
, on simplification (1) reduces to the quadratic equation in λ:
λ
2
− 5.767λ + 1.153 = 0
The two roots are λ
1
= 5.56 cm and λ
2
= 0.207 cm.
In determining surface tension it is preferable to use the shorter wavelength
because the surface effect will dominate over gravity:
8.45
v
p
=
ω
k
=
g
k
v
g
=
dω
dk
=
1
2
g
k
∴ v
g
=
1
2
v
p
