Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.


398 9 Fluid Dynamics
9.29 In prob. (9.28) if the tubes are connected in series then what quantity will flow
through the composite tube?
9.3 Solutions
9.3.1 Bernoulli’s Equation
9.1 From continuity equation
A
1
v
1
= A
2
v
2
∴ v
2
=
A
1
v
1
A
2
=
πr
2
1
v
1
πr
2
2
=
10
2
× 4
5
2
= 16 m/s
9.2
v
x
= 3x
2
− xy + 2z
2
v
y
= 2x
2
− 6xy + y
2
v
z
=−2xy − yz +2y
2
∴
∂v
x
∂x
= 6x − y;
∂v
y
∂y
=−6x + 2y;
∂v
z
∂z
=−y
∇·v =
∂v
x
∂x
+
∂v
y
∂y
+
∂v
z
∂z
= (6x − y) + (−6x +2y) − y = 0
Thus the continuity equation for steady incompressible flow is satisfied.
9.3 Pressure difference across the wing
p =
1
2
ρ(v
2
1
− v
2
2
)
=
1
2
× 1.293 × (70
2
− 55
2
) = 1212 Pa
(a) Lift = (pressure difference) (area)
= 1212 ×4 = 4848 N
(b) Net force = Lift − Weight of plane
= 4848 −(300 × 9.8)
= 1908 N in the upward direction
9.4
P =
1
2
ρv
2
A
2
a
2
− 1
A
a
=
π R
2
πr
2
=
10
5
2
= 4
9.3 Solutions 399
60,000 − 45,000 =
1
2
× 1000 × 15v
2
or v = 1.414 m / s (throat)
Rate of flow of water
Q = v A = (1.414)(π ×0.01
2
) = 0.0444 m
3
/s
9.5
v =
2ghρ
ρ
=
2 × 9.8 × 0.15 × 810
1.293
= 42.9m/s = 154.5km/h
9.6 Total area of the holes
A = 80 ×2.5 × 10
−6
m
2
= 2 ×10
−4
m
2
Q = Av
v =
Q
A
=
2 × 10
−3
2 × 10
−4
= 10 m/s
9.7
(a)
v
x
= 3xy + y
2
v
y
= 5xy + 2x
∂v
x
∂x
= 3y;
∂v
y
∂y
= 5x
∂v
x
∂x
+
∂v
y
∂y
= 3y + 5x = 0
Therefore, steady incompressible flow is not possible.
(b)
v
x
= 3x
2
+ y
2
v
y
=−6xy
∂v
x
∂x
= 6x;
∂v
y
∂y
=−6x
∂v
x
∂x
+
∂v
y
∂y
= 6x −6x = 0
Thus, steady incompressible flow is possible.
9.8
P =
1
2
ρ(v
2
1
− v
2
2
)
v
1
=
2P
ρ
+ v
2
2
=
2 × 1000
1.293
+ 100
2
= 107.45 m/s

400 9 Fluid Dynamics
9.9
(a)
Q = v
throat
a = v
pipe
A
∴ v
throat
= v
pipe
A
a
= v
pipe
D
2
d
2
= 10 ×
4
2
2
2
= 40 m/s
(b)
p =
1
2
ρv
2
A
2
a
2
− 1
=
1
2
× 1000 × 40
2
4
4
2
4
− 1
= 12 ×10
6
Pa
9.10 Reynold’s number R =
ρ Dv
η
, where ρ is density, D diameter, v velocity and
η coefficient of viscosity.
(a) R =
1 × 0.1 × 300
0.018
= 1667
Flow is steady because R < 2200
(b) R =
1 × 0.1 × 300
0.008
= 3750
Flow is turbulent because R > 2200
(c) R =
1 × 0.1 × 300
0.004
= 7500
Flow is turbulent because R > 2200
9.11 Consider a mass element dm of the fluid at distance x from the vertical axis.
The centrifugal force on dm is
dF = dm ω
2
x = dm
dv
dt
= dm
dv
dx
v
vdv = ω
2
x dx
v dv = ω
2
x d x
v
2
2
=
ω
2
2
x
2
L
L–l
∴ v = ωl
2L
l
− 1
9.12 Applying Bernoulli’s equation to points A and B,
p
A
+
1
2
ρ
g
v
2
= P
B
(1)
p
A
+ ρ
L
gh = P
B
(2)
9.3 Solutions 401
Comparing (1) and (2)
v =
2ghρ
L
ρ
g
9.13 Apply Bernoulli’s equation at the sections A
1
and A
2
:
P
1
+
1
2
ρv
2
1
= P
2
+
1
2
ρv
2
2
(1)
∴ p
2
− p
1
= p = hρg =
1
2
ρ(v
2
1
− v
2
2
)
∴ 2gh = v
2
1
− v
2
2
(2)
Q = v
1
A
1
= v
2
A
2
(3)
v
2
=
v
1
A
1
A
2
(4)
Using (4) in (2)
2gh = v
2
1
(A
2
2
− A
2
1
)
A
2
2
v
1
= A
2
2gh
A
2
2
− A
2
1
Q = A
1
v
1
= A
1
A
2
2gh
A
2
2
− A
2
1
9.14 Volume of water flowing out per second
Q = sv (1)
where v is the speed and s is the cross-sectional area.
Volume flowing out
V = Qt = svt (2)
1
2
ρv
2
= P =
F
A
=
FL
AL
=
W
V
(3)
where L is the length of the cylinder and W is the work done.
∴ W =
1
2
ρV
3
s
2
t
2
(4)
where we have used (2).

402 9 Fluid Dynamics
9.15
(a) The components of mω
2
r parallel to the x-axis and z-axis are mω
2
x and
mω
2
z, respectively. Taking y in the upward direction
dp = ρ(ω
2
xdx +ω
2
zdz − gdy) (1)
In the x − z-plane, y = constant. Hence dy = 0.
Integrating (1)
p =
ρω
2
x
2
2
+
ρω
2
z
2
2
+C
where C is the constant of integration.
p =
ρω
2
2
(x
2
+ z
2
) + C
=
1
2
ω
2
r
2
+ C
p = p
0
at r = 0, then C = p
0
∴ p = p
0
+
1
2
ρω
2
r
2
(b) Particle at P is in equilibrium under centrifugal force and gravity, Fig. 9.6.
Let PM be tangent at P(r, y) making an angle θ with the r-axis. PN is
normalatP.IfN is the normal reaction
N cos θ = mg
N sin θ = mω
2
r
∴ tan θ =
ω
2
r
g
Fig. 9.6
9.3 Solutions 403
∴
dy
dr
=
ω
2
r
g
y =
dy =
ω
2
g
rdr + c
y =
ω
2
r
2
2g
+ c
y = 0, r = 0, c = 0
y =
1
2
ω
2
r
2
g
Figure of revolution of the curve is a paraboloid.
9.3.2 Torricelli’s Theorem
9.16 Using Bernoulli’s equation
P
2
+
1
2
ρv
2
2
= P
1
+
1
2
ρv
2
1
3.1 × 10
5
+
1
2
× 1000v
2
2
= 3.5 ×10
5
+ 0
v
2
= 8.94 m/s
9.17 (a) Use Bernoulli’s equation at two points A and B at height h
A
and h
B
,
respectively, Fig. 9.7.
P + ρgh
A
= P + ρgh
B
+
ρv
2
2
(1)
where P is the atmospheric pressure, ρ is the density of water and v is the
efflux velocity.
Fig. 9.7

404 9 Fluid Dynamics
Calling h
A
− h
B
= h (2)
v =
2gh (3)
Using simple kinematics, the range
R = vt =
2gh
2(H − h)
g
R = 2
h(H −h) (4)
(b) In (4) R is unchanged if we replace h by H − h. Therefore, the second
hole must be punched at a depth H −h to get the same range.
9.18 From prob. (9.17)
R = 2
h(H −h) (1)
Maximum range is obtained by setting dR/dh = 0 and holding H as constant.
This gives h = H/2 and substituting this value in (1), we get R
max
= H.
9.19 For the water level to remain stationary volume efflux = rate of filling = x
v A =
2gh
A = x = 70 cm
3
/s
h =
x
2
2gA
2
=
(70)
2
2 × 980 × (0.25)
2
= 40 cm
9.20 Let the water level be at a height x at any instant. The efflux velocity will be
v =
√
2gx . As the water flows out, the level of water comes down, Fig. 9.8.
Fig. 9.8
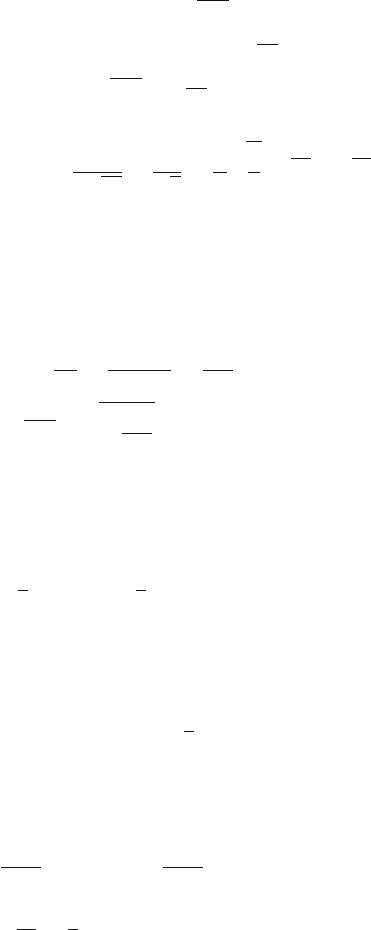
9.3 Solutions 405
Volume flux, Q = av = a
√
2gx
Volume flux is also equal to Q = A
dx
dt
We then have a
√
2gx = A
dx
dt
t =
dt =
A
a
√
2g
h
1
h
2
dx
√
x
=
A
a
2
g
h
1
−
h
2
9.21 Pressure at the bottom due to water column = (3 − 1) atm = 2atm= 2 ×
10
5
Pa.
P = hρg
∴ h =
P
ρg
=
2 × 10
5
1000g
=
200
g
v =
2gh =
2g
200
g
= 20 m/s
Second method
Apply Bernoulli’s equation
P
1
+
1
2
ρv
2
1
= P
2
+
1
2
ρv
2
2
where the left side refers to the point inside the tank and right side to a point
outside the tank.
3 × 10
5
+ 0 = 1 × 10
5
+
1
2
× 1000v
2
2
∴ v
2
= 20 m/s
9.22 Q = v
1
A
1
= v
2
A
2
2gh
1
(2A
2
) =
2gh
2
A
2
∴
h
1
h
2
=
1
4
9.23 Apply Bernoulli’s equation to a point just outside the hole and a point at the
top of the kerosene surface. If P is the atmospheric pressure, h
1
and h
2
the
heights of water and kerosene columns, respectively, ρ
1
and ρ
2
the respective
densities,
406 9 Fluid Dynamics
P +
1
2
ρ
1
v
2
1
= P + h
1
ρ
1
g + h
2
ρ
2
g
∴ v
1
=
2g
h
1
+
h
2
ρ
2
ρ
1
Substituting h
1
= 60 cm, h
2
= 40 cm, ρ
1
= 1, ρ
2
= 0.8 and g = 980, we
find v
1
= 425 cm/s or 4.25 m/s.
9.24 Volume efflux at A and B, Fig. 9.9
Fig. 9.9
Q
A
= v
A
S
Q
B
= v
B
S
(Mass efflux)
A
= ρv
A
S
(Mass efflux)
B
= ρv
B
S
Force F
A
= (rate of change of momentum)
A
= ρv
A
Sv
A
= ρ Sv
2
A
= ρ S(2gh) = 2ρSgh
F
B
= 2ρ Sg(h + h)
F
B
− F
A
= 2 ρ Sg h
(because the vector force is in the opposite direction)
= 2 ×1000 × 1.0 × 10
−4
× 9.8 × 0.51 = 1.0N
9.3.3 Viscosity
9.25 Volume of liquid flowing per second
V =
πr
4
P
8ηl
9.3 Solutions 407
P =
8ηlV
πr
4
=
8 × 0.001 × 4000 × 0.002
3.14 × (0.04)
4
= 0.0796 ×10
5
Pa
Pressure head h =
P
ρg
=
0.0796 × 10
5
1000 × 9.8
= 0.8m
9.26
P
A
− P
B
=
8ηl
1
Q
π r
4
=
8ηQ
π
(0.16)
(2 × 10
−3
)
4
=
8ηQ (0.01)
π ×10
−12
(1)
P
B
− P
0
=
8ηQ × (0.04)
π ×10
−12
(2)
Adding (1) and (2)
P
A
− P
0
=
8ηQ × 0.05
π ×10
−12
(3)
Dividing (2) by (3)
P
B
− P
0
P
A
− P
0
= 0.8
∴ P
B
− P
0
= 0.8 ×(P
A
− P
0
) = 0.8 × 3 = 2.4 cm of water.
9.27 The terminal velocity v
T
is given by
v
T
=
2
9
r
2
g
(ρ
1
− ρ
2
)
η
(1)
where r is the radius of the drop, ρ
1
and ρ
2
are the densities of the drop and
air, respectively, g is the gravity and η is the coefficient of viscosity. If the new
radius is r
and the new terminal velocity v
T
, then
v
T
v
T
=
r
2
r
2
(2)
Under the assumption that the drops are incompressible, the volume remains
constant:
4π
3
(r
)
3
= 2 ×
4π
3
r
3
∴ r
= 2
1/3
r (3)
Using (3) in (2)
v
T
= 2
2/3
v
T
= 4
1/3
v
T
