Кадомская К.П. Перенапряжения в электрических сетях различного назначения и защита от них
Подождите немного. Документ загружается.


[]
).cos(
22
0
2
0
sinsincoscos
22
0
2
0
)(
вын
ψ+ω
ω−ω
ω
=ωψ−ωψ
ω−ω
ω
= t
m
E
tt
m
E
t
C
u (2.4)
[][]
)()0()0()(
пер0
2
вын0
2
2
вын0пер
ψ−ω−+−= tсоsiiZuutu
C
. (2.5)
В выражениях (2.4) и (2.5) применены следующие обозначения:
ψ
ω−ω
ω
= cos)0(
22
0
2
0
вын
m
E
u ,
ψ
ω−ω
ω
ω
−= sin)0(
22
0
0
вын
m
E
Zi ,
C
L
Z = ,
[]
)0(
)0(
вын0
вын0
пер
uu
iiZ
arctg
−
−
=ψ
.
При частоте собственных колебаний контура, существенно
превышающей промышленную частоту (
)
0
ω
>>
ω
максимум напряжения
на емкости наступает примерно в момент времени
0
пер
ω
ψ
+
π
=
m
t .
К этому моменту времени вынужденная составляющая практически
будет равна своему начальному значению, т.е.
)0()(
вынвын
utu
mC
≅
.
Переходная же составляющая в этот момент времени будет иметь
максимальное значение, совпадающее по знаку с вынужденной
составляющей напряжения на емкости. Поэтому при пренебрежении
затуханием переходной составляющей к этому моменту времени максимум
напряжения на емкости можно оценить как:
[][]
2
вын0
2
2
вын0)0(вынmax
)0()0( iiZuuuU
C
−+−+= . (2.6)
В случае учета затухания переходной составляющей максимум
перенапряжений можно оценить с помощью выражения:
[][]
)1()0()0(
уд
2
вын0
2
2
вын0)0(вынmax
−−+−+= kiiZuuuU
C
. (2.7)
В (2.7) k
уд
– ударный коэффициент, обычно принимаемый при
реальных потерях в элементах электропередачи в диапазоне 1,7…1,9.
Из выражения (2.7) видно, что переходная составляющая а,
следовательно, и максимум перенапряжений зависят как от момента
шунтирования резистора, характеризуемого углом
ψ, так и от величины

энергии, запасенной в индуктивности и емкости перед началом
коммутации, характеризуемой начальными значением тока i
0
и
напряжения на емкости u
0
, соответственно. В случае i
0
=0 и k
уд
=2 максимум
напряжения на емкости можно оценить как:
0вынmax
)0(2 uuU
C
−
=
. (2.8)
В приведенных выражениях (2.6)-(2.8) вынужденная составляющая
может быть определена с учетом распределенности параметров ВЛ.
Так, например, при включении холостой заряженной линии
вынужденная составляющая напряжения в конце холостой линии при t=0
определится как:
)cos(
cos
/)0(
вын
s
s
m
Eu
α+λ
α
=
,
где
)5.0()/(
В
arctgZLarctg
s
=ω=α
, λ - волновая длина ВЛ на частоте
50 Гц.
При длине линии 300 км, внутреннем сопротивлении системы равным
половине волнового сопротивления ВЛ (
2/
В
ZL
=
ω
) и включении ВЛ в
момент максимума э.д.с. (
ψ= 0)
=
m
Eu /)0(
вын
1,26. В случае же включения
ВЛ, заряженной до напряжения –0,5E
m
, максимум напряжения в конце ВЛ
при её включении в случае пренебрежения затуханием переходной
составляющей составит – U
max
/E
m
=3,02.
2.2 УРАВНЕНИЯ ЛИНИИ ЭЛЕКТРОПЕРЕДАЧИ
И ИХ РЕШЕНИЕ
Процессы, сопровождающиеся перенапряжениями грозового и
коммутационного происхождения, происходят в схемах, как правило,
содержащих элементы с распределенными параметрами – надземные и
подземные линии электропередачи. Переходные процессы в этих
элементах описываются уравнениями в частных производных,
гиперболического типа относительно независимых переменных времени t
и координаты по трассе линии x. В случае линейной постановки задачи
(первичные
погонные параметры линий не зависят от тока и напряжения),
а также при пренебрежении зависимостью этих параметров от частоты,
уравнения гиперболического типа, описывающие волновые процессы в
однопроводной линии, имеют вид:
),(
),(
)(
),(1),(
2
2
22
2
txRGu
t
txu
CRGL
t
txu
v
x
txu
+
∂
∂
+=
∂
∂
−
∂
∂
, (2.9)
txRGi
t
txi
CRGL
t
txi
v
x
txi
,(
),(
)(
),(1),(
2
2
22
2
+
∂
∂
+=
∂
∂
−
∂
∂
). (2.10)
где ),(
t
x
u и ),(
t
x
i - напряжение и ток в точке линии с координатой x в
момент времени t, L, R, C, G – погонные индуктивность, активное
сопротивление, емкость и активная проводимость линии,
00
/1 μεε=v
-
скорость распространения волны по линии,
ε
0
– диэлектрическая
постоянная,
ε - диэлектрическая проницаемость изоляционной среды, в
которой распространяются волны,
μ
0
– магнитная постоянная.
В случае пренебрежения потерями в канале передачи энергии
решение уравнений (2.9) и (2.10) представляет собой сумму двух волн,
движущихся в направлении возрастания [)( v
t
x
f
−
] и убывания [)( v
t
x
+ψ ]
координаты x по характеристикам
cons
t
v
t
x
=
−
и cons
t
v
t
x
=
+
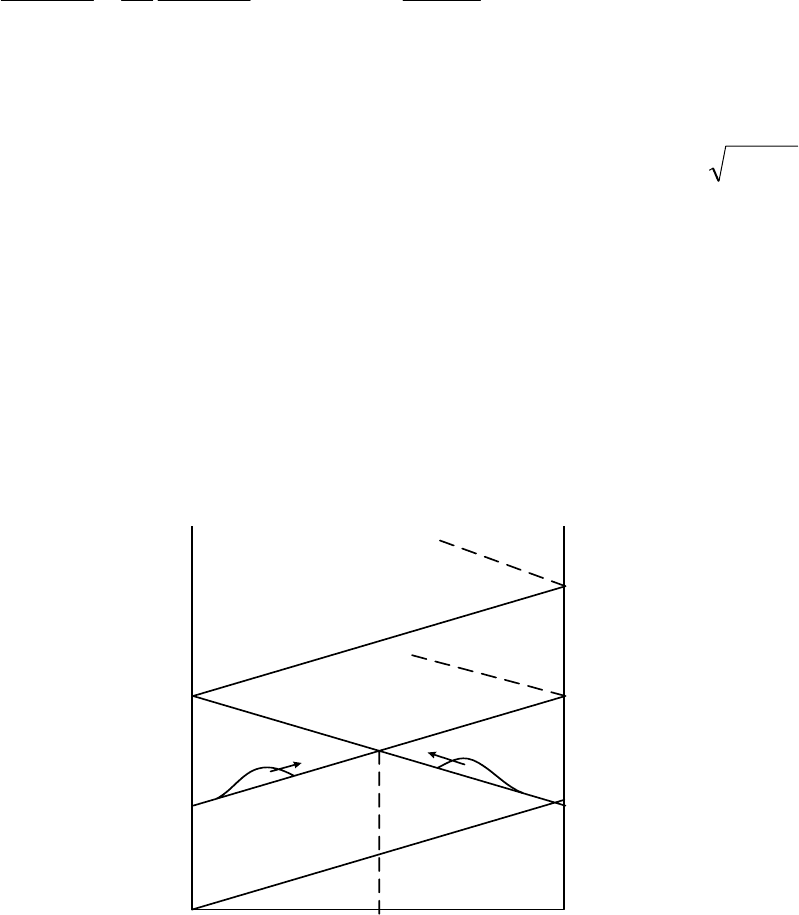
(рис.2.3):
+
−
= )(),( c
t
x
f
t
x
u )( с
t
x
+
ψ
. (2.11)
τ
2τ
τ
2τ
3τ
t
t
0 xl
f(x-vt)
ψ(x+vt)
t
Рис.2.3 Характеристическая сетка
2.3 МЕТОД БЕГУЩИХ И СТОЯЧИХ ВОЛН
Приведенный выше метод характеристик решения уравнения в
частных производных гиперболического типа приводит к решению в виде
бегущих волн. Вместе с тем в ряде случаев можно получить решение и в
виде стоячих волн, т.е. в каждой точке линии решение может быть
представлено не в виде бегущих волн, распространяющихся в начало и
конец линии, а в виде разложения решения в бесконечный ряд по
составляющим различных частот (стоячих волн).
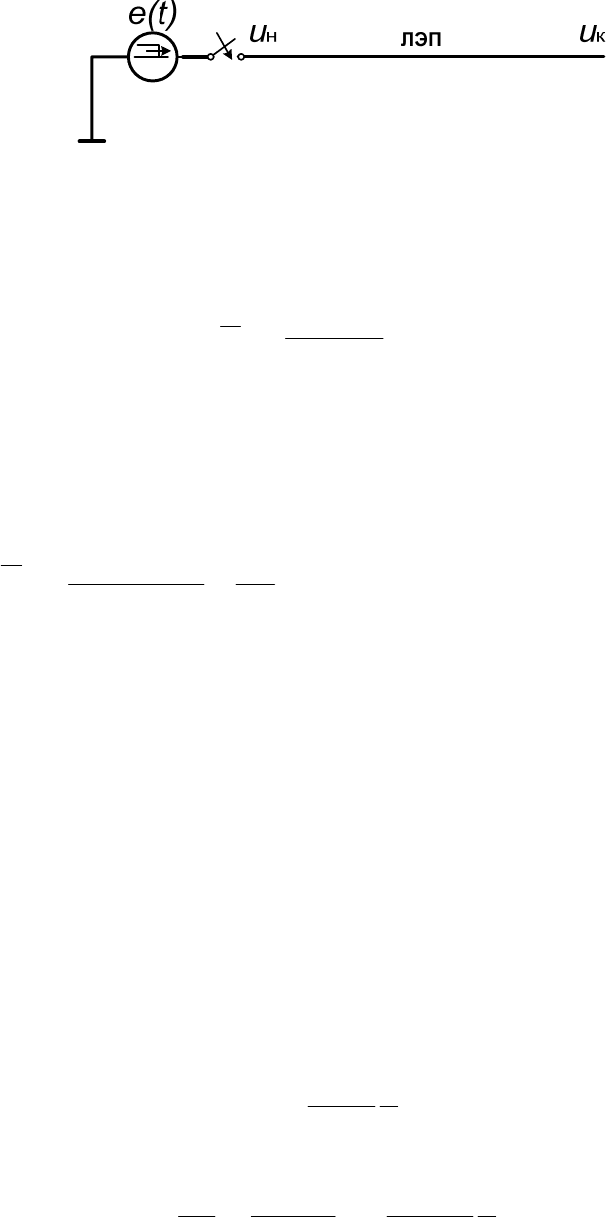
Поясним эти методы решения на простейшем примере включения
прямоугольной э.д.с. на холостую линию при неучете потерь. (рис.2.4).
Рис.2.4. Расчетная схема
При включении прямоугольной единичной э.д.с. операторное
изображение напряжения в конце ЛЭП запишется в виде:
=
к
U
)( τppch
E
, (2.12)
где
τ - время пробега волны по ЛЭП.
Для того, чтобы получить оригинал в виде бегущих волн, перепишем
выражение (2.12) в виде:
....)(
2
)1(
2
53
2
к
−+−=
+
=
τ−τ−τ−
τ−
τ−
ppp
p
p
eee
p
E
ep
Ee
U
. (2.13)
Оригинал выражения (2.13), полученный с помощью теоремы
запаздывания, записывается в виде:
[]
...)7()5()3()(2)(
0000
+
τ
−
δ
−
τ
−
δ
+
τ
−
δ
−τ−δ= ttttEtu
k
, (2.14)
где
))12((
0
τ−−δ kt
=
⎩
⎨
⎧
δ )(
0
0
t
при
при
τ−≥
τ
−
<
)12(
)12(
kt
kt
- обобщенная единичная
функция.
Решение (2.14) записано в форме бегущих волн.
Оригинал от (2.12) можно взять, воспользовавшись второй теоремой
разложения Хевисайда. Корни знаменателя при этом будут:
0
=
p
и
2
12
π
τ
−
±=
k
jp
k
, где
∞
=
...1k .
В этом случае оригинал записывается в виде:
)
2
)12(
cos(
12
)1(4
)(
1
1
к
t
k
k
E
Etu
k
k
π
τ
−
−
−
π
−=
∑
∞
=
+
. (2.15)
Решение представлено в виде бесконечного ряда составляющих
различных частот. Причем первая частота собственных колебаний (при
k=1) обратно пропорциональна двойному времени пробега волны по ЛЭП.
С увеличением частоты амплитуды составляющих уменьшаются обратно
пропорционально частоте. На рис. 2.5 приведены результаты расчетов при
включении воздушной линии длиной 300 км при удержании 13 членов
ряда в (2.15). Решение же
в виде бегущих волн (2.13) представляет собой
ряд прямоугольников с амплитудой 2E (рис.2.6). Из приведенного примера
видно, что в случае существенного веса высших гармоник в кривой
напряжения решение в виде стоячих волн требует учета большого числа
гармоник. Поэтому целесообразно использовать этот метод в случае
несущественного вклада в решение высших гармоник: например, при
включении
холостой ЛЭП с волновым сопротивлением w на шины,
моделируемые в виде источника синусоидальной э.д.с. с внутренним
индуктивным сопротивлением. Расчетная схема в этом случае приведена
на рис. 2.7.
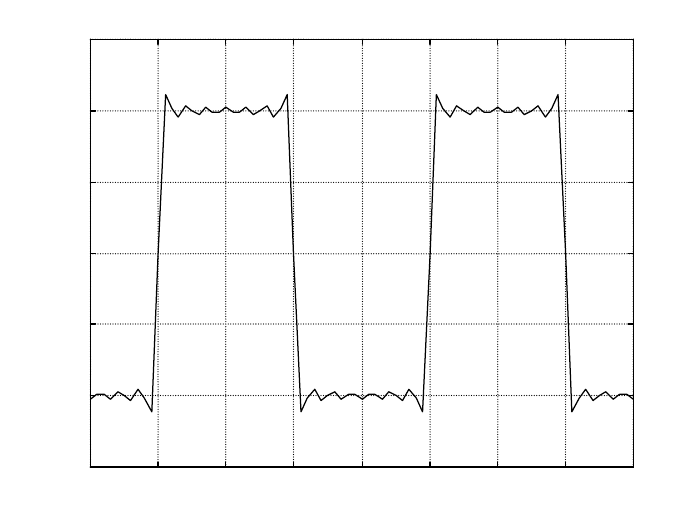
Рис.2.5 Решение методом стоячих волн (учтено 13 гармоник)
0 1 2 3 4 5 6 7 8
x 10
-3
-1.5
-1
-0.5
0
0.5
1
1.5
s
u/Em
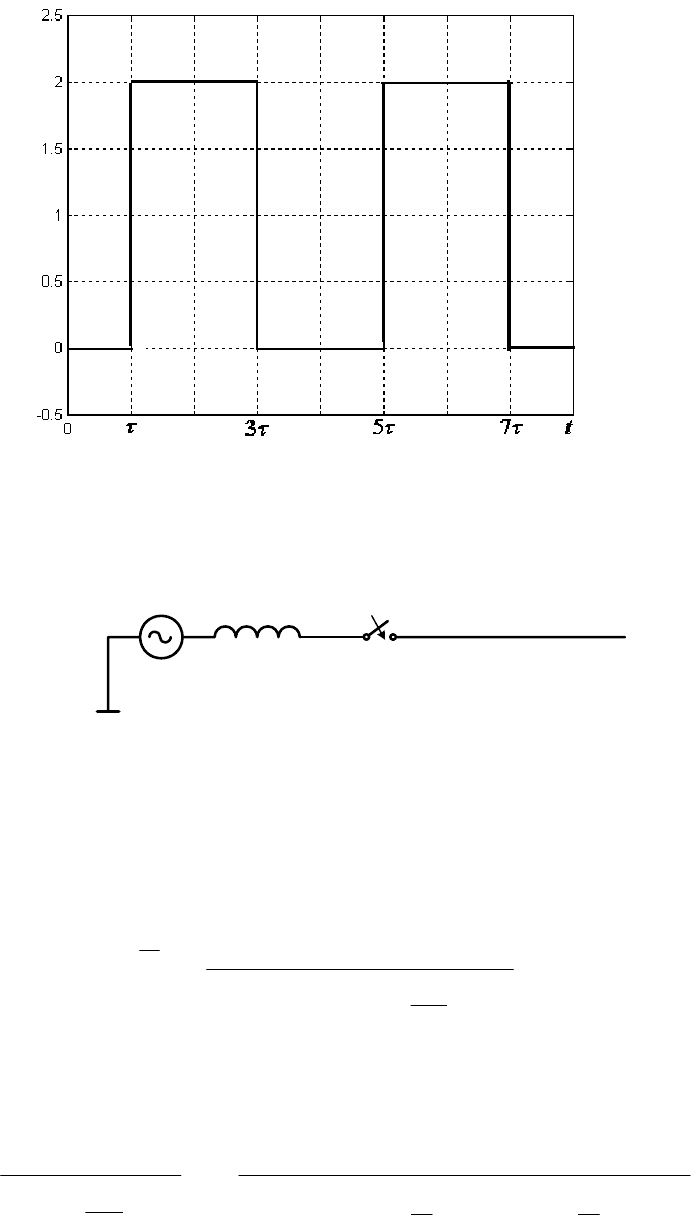
Рис.2.6. Решение методом бегущих волн
L
e(t)
u
к
w, τ
Рис.2.7 Расчетная схема при включении холостой ВЛ
на шины системы
Операторное изображение напряжения в конце холостой линии без
потерь при
ψ =0 имеет вид:
))((
22
к
τ+τω+
=
shp
w
pL
chpp
pE
U
m
, (2.16)
Применяя вторую теорему разложения, получим оригинал в виде:
,
cossin)()(
cos2
sincos
cos
)(
22
к
∑
⎥
⎦
⎤
⎢
⎣
⎡
λλ+λ+τβ−ω
β
β
+
λ
ω
−λ
ω
=
k
kkkk
kkmm
w
L
w
L
tE
w
L
tE
tu
(2.17)
где
λ= ωτ - волновая длина линии на промышленной частоте,

λ
k
= β
к
τ - волновая длина линии на частоте собственных колебаний β
k
.
Частоты собственных колебаний определяются из
характеристического уравнения
0=τ+τ shp
w
pL
chp при p
k
=±jβ
k
(корни
являются сопряженными мнимыми, так как не учтены активные
сопротивления элементов схемы рис.2.7). Уравнение для определения
β
k
имеет вид:
kк
w
L
ctg
λ
λ
ω
=λ . (2.18)
Напряжение в конце линии длиной 300 км при её включении на шины
системы (x/w=0.5) при учете первых трех свободных составляющих
записывается в виде:
t
t
t
t
t
u ω
−
ω
+
ω
−
ω= 3.20cos025.046.10cos110.029.2cos341.1cos255.1)(.
Из приведенного выражения видно, что при подключении ВЛ к
источнику конечной мощности можно при приемлемой точности решения
учесть лишь три свободных составляющих. Напряжение в конце ВЛ в виде
графика приведено на рис.2.8. Из рисунка видно, что с
помощью метода
стоячих волн достаточно точно получено запаздывание напряжения в
конце ВЛ (при длине ВЛ 300 км запаздывание составляет 1 мс). Cледует
отметить, что метод стоячих волн позволяет получить частотный спектр
исследуемых процессов.
Рис.2.8. Напряжение в конце ВЛ при её включении на шины
системы конечной мощности
0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018 0.02
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
s
u/Em

2.4 МЕТОД ОБОБЩЕННЫХ БЕГУЩИХ ВОЛН
Метод обобщенных бегущих волн целесообразно использовать в
схемах, содержащих несколько узловых точек, соединенных между собой
линиями с распределенными параметрами. Конечное время
распространения волн по ЛЭП позволяет решать уравнения, описывающие
процессы в узлах (рис.2.9), независимо друг от друга.
i
x
z
x
x
i
k
z
k
k
V
kx
V
xk
W
xk
W
kx
w
kx
τ
kx
Рис.2.9 К расчету схемы методом обобщенных бегущих волн
Для всех узлов сети составляются уравнения вида:
)()()( tVtiwtu
эxxэxx
=
+
, (2.19)
[
]
)()( tiNtu
xx
=
.
где
∑
=
k
kx
эx
kxэx
w
w
VV - эквивалентная волна в узле "x",
эx
w
- параллельное соединение волновых сопротивлений в узле "х",
[]
)(tiN
x
- линейный или нелинейный оператор.
Из уравнений (2.19) в момент времени t определяются напряжения и
токи. Затем во всех узлах и для всех линий определяются обобщенные
отраженные волны:
).()(2)()(2)( tVtiwtVtutW
kxxэxxkxxk
−
=
−
=
(2.20)
При неучете потерь в ВЛ волны, отраженные от узла "х", будут
падающими для узлов "k" через времена, равные временам пробега от узла
"х" до узла "k". В случае учета затухания волны эти волны можно
определить как:
)()()(
0
xkxkxkxkxk
tmtWtV
τ
−
δ
τ
−
=
, (2.21)

где m
xk
– коэффициент затухания обобщенной волны.
2.5 УЧЕТ ИСКАЖЕНИЯ ВОЛН ПРИ ИХ ПРОБЕГЕ ПО ЛЭП
2.5.1 УРАВНЕНИЯ КАНАЛА ЛЭП ПРИ ЧАСТОТНО ЗАВИСИМЫХ
ПРОДОЛЬНЫХ ПАРАМЕТРАХ И ИХ РЕШЕНИЕ
В приведенные выше методах бегущих и стоячих волн не
учитывалось то обстоятельство, что продольные параметры ЛЭП являются
частотно-зависимыми. При исследовании ряда электромагнитных
процессов, например, при диагностике ЛЭП или при передаче аналоговой
или цифровой информации по каналам воздушных или кабельных линий
такой учет необходим. Рассмотрим учет частотных зависимостей
параметров ЛЭП на
примере задачи импульсной диагностики таких
неоднородностей, как коррозия металлической оболочки и водные триинги
в кабельных линиях высокого напряжения однофазного исполнения с
пластмассовой изоляцией. Анализ показывает, что для эффективного
распознавания указанных неоднородностей диагностические импульсы
должны быть по-возможности прямоугольными и иметь конечную
длительность, измеряемую наносекундами и десятками наносекунд.
Прямоугольный импульс напряжения
конечной длительности может быть
получен наложением двух прямоугольных импульсов бесконечной
длительности:
()
(
)
(
)
[
]
τ
−
δ
−
δ
=
τ ttUu
00
, (2.22)
где
()
t
0
δ
- единичная функция,
(
)
τ
−
δ
t
0
- обобщенная единичная функция:
()
⎩
⎨
⎧
τ>
τ
<
=τ−δ
. tпри ,1
, tпри ,0
0
t
Следовательно, для анализа искажения прямоугольного импульса
конечной длительности при распространении его по каналу ЛЭП следует
рассмотреть искажение прямоугольного импульса бесконечной
длительности.
Уравнения длинной линии относительно комплексных амплитуд
напряжений и токов запишутся в виде:
⎪
⎪
⎭
⎪
⎪
⎬
⎫
=−
=−
,
,
UY
dx
Id
IZ
dx
Ud
&
&
&
&
, (2.23)
где Z и Y – погонные продольное и поперечное сопротивления линии.
Решение системы уравнений (2.23) относительно комплексной
амплитуды напряжения будет:
xx
Be
A
eU
⋅
γ
⋅
γ
−
+
=
&
, (2.24)
где
ZY=γ - коэффициент распространения волны, зависящий от
частоты.
Решение для волны, движущейся в прямом направлении (в сторону
возрастания координаты x), запишется как:
()
x
AexU
⋅
γ
−
=
&
. (2.25)
При включении ВЛ на шины источника прямоугольного импульса с
амплитудой U
0
(при пренебрежении внутренним сопротивлением этого
источника), получим:
() ()
xx
eUeUxU
⋅γ−
⋅
⋅γ−
==
0
0
&&
. (2.25)
Перепишем решение (2.25), записанное в частотной области, в
операторной форме:
()
(
)
(
)
xp
epUpxU
⋅
γ
−
= ,0,
, (2.26)
где
() ()
(
)
pYpZp =γ
- операторный коэффициент распространения.
Операторный коэффициент распространения может быть записан как в
[2]:
()
(
)
(
)
ppp
*
0
γ+γ=γ
, (2.27)
()
000
εεμμ=γ
rr
pp
- операторный коэффициент распространения,
характеризующий распространение волны в диэлектрике,
()
p
*
γ - составляющая операторного коэффициента распространения,
характеризующая искажение сигнала при пробеге по ЛЭП.
Подставляя (2.27) в (2.26), получим
() ()
(
)
xp
epUpxU
⋅γ−
=
*
*
, , (2.28)
где
()
(
)
(
)
xp
epUpU
0
0
*
γ−
=
.
Если принять, что посылается прямоугольный сигнал бесконечной
длительности, то
