К компетенциям - через инноватику

Подождите немного. Документ загружается.

и здоровья людей. Для своевременного обнаружения дефектов машин

и прогнозирования ресурса работы требуются эффективные системы

диагностирования, интегрированные в систему управления и осна-

щенные развитой системой интеллектуальных датчиков с беспровод-

ными технологиями передачи информации.

В настоящее время происходит «революция» в системах диагно-

стирования машин, которая обусловлена развитием широкого спек-

тра интеллектуальных датчиков с передачей информации по беспро-

водным технологиям, появлением высокопроизводительных вычис-

лительных систем и развитием методов искусственного интеллекта

на основе нейронных сетей.

В связи с повышением требований к качеству, точности и надеж-

ности станков с ЧПУ возрастает роль технической диагностики на

стадиях производства, эксплуатации, текущего и капитального ре-

монта станков.

Диагностика требуется при приемо-сдаточных испытаниях

станков на заводе-изготовителе. Диагностика станков является

основной процедурой для определения необходимости и возмож-

ности проведения ремонта станков. Большинство станков на тер-

ритории России находятся в эксплуатации не менее десяти лет, что

приводит к естественному износу деталей и узлов механической

структуры.

С целью выявления узла, который в первую очередь нуждается

в диагностировании, был проведен анализ влияния узлов токарного

станка ИТ-42 на качество обработки деталей и частоты появления

дефектов в данных узлах на заводе «Ижмаш» в соответствии с мето-

дикой обработки значений экспертных оценок.

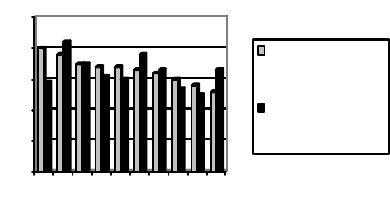
Результаты обработки значений экспертных оценок приведены

на рис. 1, где оценки экспертов по существенности влияния узлов

станка на качество обработки деталей приведены на диаграмме:

4 – очень существенная роль, 3 – существенная роль, 2 – малосу-

щественная роль, 1 – несущественная роль; оценки экспертов по

частоте появления дефектов узлов: 5 – дефекты встречаются очень

часто, 4 – часто, 3 – иногда, 2 – редко, 1 – очень редко. Узлы стан-

ка: шпиндельный узел, УЧПУ – устройство ЧПУ, ПВГ – передача

винт – гайка, РГ – револьверная головка, ПП – привода подач,

ПГД – привод главного движения, СС – система смазки, ЗБ – зад-

няя бабка, П – патрон, СОЖ – смазочно-охлаждающая жидкость.

1 2 3 4 5 6 7 8 9 10

влияние на

качество обработки

деталей

частота появления

дефектов узлов

Рис. 1. Оценка экспертов по влиянию узлов токарных станков на качество

обработки деталей и по частоте появления дефектов: 1 – ШУ, 2 – ПВГ,

3 – ПП, 4 – ЗБ, 5 – ПГД, 6 – ЗБ, 7 – П, 8 – СС, 9 – СОЖ, 10 – УЧПУ

В связи с тем, что шпиндельный узел в наибольшей степени влия-

ет на качество обрабатываемых деталей, он был выбран как объект

диагностирования.

Существует несколько способов диагностирования:

– по вибрации,

– по температуре,

– по анализу частиц металла в масле,

– по мощности.

В данной работе используется диагностика по вибрации, исходя

из того, что:

– колебательные силы возникают непосредственно в месте появ-

ления дефекта;

– вибрация содержит максимальный объем диагностической ин-

формации;

– диагностировать можно на месте, без разборки и остановки обо-

рудования.

Устройство диагностирования состоит из датчика ускорения со

встроенным усилителем, цифрового сигнального процессора со встро-

енным аналого-цифровым преобразователем и персонального компью-

тера.

В качестве преобразователя механических колебаний в электриче-

ский сигнал используется датчик ускорений MMA6333Q. Этот датчик

имеет надежный корпус, в котором находятся емкостной чувствитель-

ный элемент, встроенный усилитель сигнала, фильтр низких частот,

схема температурной компенсации. В роли преобразователя данных

выступает быстродействующий цифровой сигнальный процессор

TMS320F2808. Он выполняет преобразование сигнала из аналоговой

формы в цифровую, накопление и передачу данных в персональный

компьютер, где происходит обработка на базе нейронной сети.

Для диагностирования шпиндельного узла выбрана сеть обратно-

го распространения ошибки, так как она позволяет минимизировать

ошибку работы многослойного перцептрона. В качестве алгоритма

обучения используется алгоритм обучения Уидроу – Хоффа.

В качестве входных данных нейронной сети используется частота

вибрационного сигнала и амплитуда этого сигнала. Наличие той или

иной частотной составляющей в спектре вибрации говорит о возник-

новении соответствующего дефекта, а амплитуда – о глубине дефекта.

Частоты проявления различных дефектов шпиндельного узла опре-

деляются по известным выражениям, приведенным в литературе [3].

Для построения системы диагностики на базе нейронной сети вы-

браны следующие параметры нейронной сети.

Менее всего, сравнительно с другими сигмоидами, процессорно-

го времени требует расчет рациональной сигмоиды. Для вычисле-

ния гиперболического тангенса требуется больше всего тактов ра-

боты процессора. Если же сравнивать с пороговыми функциями

активаций, то сигмоиды рассчитываются очень медленно. Если по-

сле суммирования в пороговой функции сразу можно начинать

сравнение с определенной величиной (порогом), то в случае сиг-

моидальной функции активации нужно рассчитать сигмоид (затра-

тить время в лучшем случае на три операции: взятие модуля, сло-

жение и деление), и только потом сравнивать с пороговой величи-

ной (например, нулем). Если считать, что все простейшие операции

рассчитываются процессором за примерно одинаковое время, то

работа сигмоидальной функции активации после произведенного

суммирования (которое займет одинаковое время) будет медленнее

пороговой функции активации как 1 : 4.

Выбрана экспоненциальная сигмоида (функция Ферми), так как

она работает с непрерывными значениями от [–1; 1], и требует не

много времени на расчет функции.

Быстродействие нейронной сети по обработке диагностической

информации зависит от числа нейронов в слоях нейронной сети. Для

оценки числа нейронов в скрытых слоях однородных нейронных се-

тей использовалась формула для определения необходимого числа

синаптических весов

в многослойной нейронной сети с сигмо-

видными передаточными функциями [1]:

1 1

(1 log ) (1 )( 1) ,

mN n L m Nm n m m

− −

+ ≤ ≤ + + + +

где n – размерность входного сигнала; m – размерность выходного

сигнала; N – число элементов обучающей выборки.

Если в сети слишком мало нейронов или слоев, то сеть не обучит-

ся и ошибка при работе сети останется большой. Если нейронов или

слоев слишком много, то быстродействие сети будет низким, потре-

буется много памяти, сеть переобучится, т. е. выходной вектор будет

передавать незначительные и несущественные детали на выходе, на-

пример, шум или ошибочные данные, зависимость выхода от входа

окажется резко нелинейной, сеть будет неспособна к обучению.

Для подготовки данных для входа и выхода используется масшта-

бирование, чтобы привести данные в допустимый диапазон. Если

отсутствует масштабирование, то нейроны входного слоя окажутся

в постоянном насыщении или все время будут заторможены, что

сильно снижает точность.

Разработанная нейронная сеть состоит из слоев – входного, вы-

ходного и скрытых. Чем более нелинейная задача, тем больше долж-

но быть скрытых слоев. В нашем случае задача однозначна, на вход

подаются информативные данные – на выходе получаем процент

ошибки, необходимы вычисления только весовых коэффициентов.

Выбрано четыре слоя: один входной, два скрытых для присвоения

весовых коэффициентов и вычисления выходных параметров с уче-

том весовых коэффициентов, один выходной.

В нейросети, как правило, все элементы предыдущего слоя связа-

ны со всеми элементами последующего. Количество нейронов в пер-

вом и последнем слое зависит от того, сколько полей указано, как

входных, так и выходных. В нашем случае их пять. Входные характе-

ристики заданы парами – это частота и амплитуда. Общих правил

определения количества нейронов нет, но необходимо, чтобы число

связей между нейронами было меньше количества примеров в обу-

чающей выборке. Иначе нейросеть потеряет способность к обобще-

нию, а просто «запомнит» все приметы из обучающей выборки. То-

гда при тестировании на примерах, присутствующих в обучающей

выборке, она будет демонстрировать прекрасные результаты, а на

реальных данных – очень плохие. Заданы пять нейронов в скрытом

слое, так как в этом слое формируются веса для каждого нейрона, то

пяти нейронов для полной работы сети достаточно [2].

Коэффициент скорости обучения нейронной сети a определяет

амплитуду коррекции весов на каждом шаге обучения.

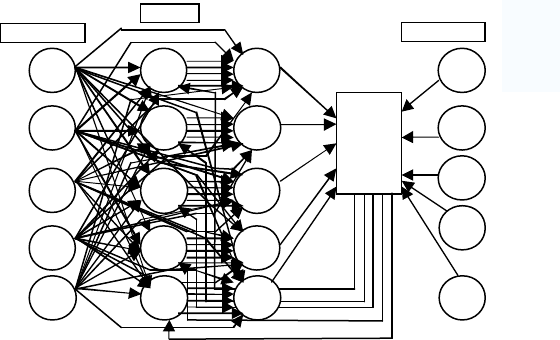
На рис. 2 представлена нейронная сеть, определяющая состояние

шпиндельного узла.

Рис. 2. Нейронная сеть диагностики шпиндельного узла

Слой Х – входной слой.

Слой S – слой формирования весовых коэффициентов.

Слой А – слой нейронной сети, где высчитываются значения, учи-

тывая полученные веса.

Слой Y – выходной слой.

Входной слой содержит входные данные, заданные в виде двумер-

ного массива амплитуды и частоты составляющей спектра вибрации.

W1, W2, W3, W4, W5 – веса, присвоенные нейронной сетью.

d(W1)/dt=a*X1*err1; d(W2)/dt=a*X2*err2; d(W3)/dt=a*X3*err3;

d(W4)/dt=a*X4*err4; d(W5)/dt=a*X5*err5;

err1, err2, err3, err4, err5 – ошибка сети; err1=Y1-A1, err2=Y2-A2,

err3=Y3-A3, err4=Y4-A4; err5=Y5-A5;

A1 = W1*X1+W2*X2+W3*X3+W4*X4+W5*X5,

A2 = W1*X1+W2*X2+W3*X3+W4*X4+W5*X5,

A3 = W1*X1+W2*X2+W3*X3+W4*X4+W5*X5,

A4 = W1*X1+W2*X2+W3*X3+W4*X4+W5*X5,

A5 = W1*X1+W2*X2+W3*X3+W4*X4+W5*X5.

Диагностика шпиндельных узлов станка с применением нейрон-

ных сетей дает:

– уменьшение времени простоя станка;

– снижение доли брака;

– повышение производительности, эффективности, надежности,

срока эксплуатации оборудования;

– уменьшение времени ремонта, улучшение его планирования.

Блок

ошибки

слой

Выхо дной

Входной слой

Список литературы

1. Круглов В. В., Борисов В. В. Искусственные нейронные сети. Теория

и практика. – М. : Горячая линия. Телеком, 2001. – 382 с.

2. Заенцев И. В. Нейронные сети: основные модели. – Воронеж : Изд-во

ВГУ, 1999. – 76 с.

3. Мэтью Д., Альфредсон Р. Применение вибрационного анализа для кон-

троля технического состояния подшипников качения // Конструирование

и технология машиностроения. – М. : Мир, 1984. – Т. 106, № 3. – С. 100–108.

Ю. Л. Караваев, П. В. Лекомцев,

аспиранты кафедры «Мехатронные системы»

Ижевский государственный технический университет

Определение силы резания на главной режущей кромке сверла©

В настоящее время имеется большое количество эмпирических

формул для расчета крутящего момента М и осевой силы P

при свер-

лении различных материалов [2, 4]. Данные зависимости с опреде-

ленной точностью позволяют подобрать оптимальные режимы реза-

ния при сверлении по мощности шпинделя и механизма главной осе-

вой подачи конкретного станка. Расчет общей силы резания F

рез

на

одной режущей кромке сверла по известным значениям крутящего

момента и осевой силы является актуальным, к примеру, для иссле-

дования процессов высокоскоростного сверления, а также количест-

венного сравнения силовых параметров сверления с такими видами

обработки, как точение и фрезерование.

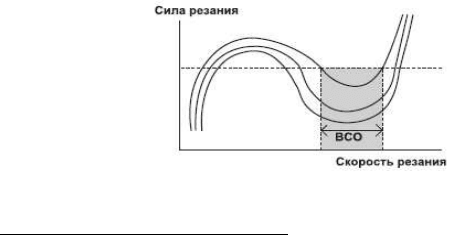
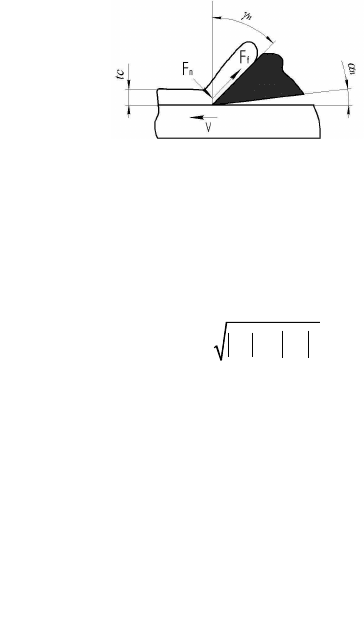
Как известно, в зоне высокоскоростной обработки металлов на-

блюдается эффект снижения сил резания (рис. 1).

Рис. 1. Характерные зависимости сил резания от скорости [1]

При сверлении различных материалов на практике с увеличением

скорости резания [3] наблюдались снижение крутящего момента

и повышение осевой силы. В таком случае сложно говорить об эф-

фекте ВСО, поскольку суммарная сила резания не оценивалась.

В статье предложен метод расчета силы резания на главной ре-

жущей кромке при сверлении по известным значениям крутящего

момента и осевой силы для стандартного спирального сверла. В ос-

нову метода положена модель элементарных сил при косоугольном

резании [5].

Распределение сил по режущим кромкам сверла

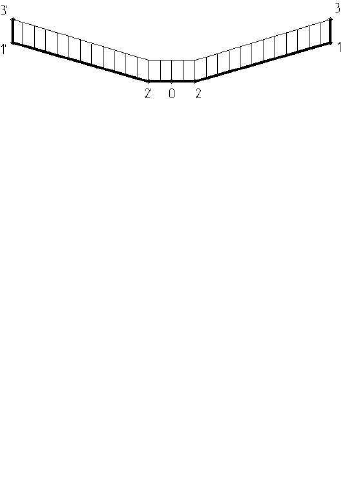
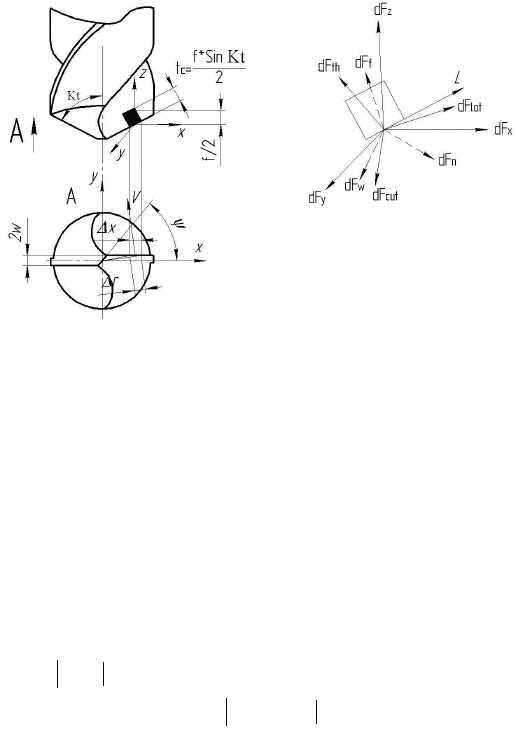
На рис. 2 схематично представлен слой материала, срезаемый ре-

жущими кромками стандартного сверла: перемычкой 0-2, главной

режущей кромкой 1-2 и вспомогательной режущей кромкой 1-3.

Рис. 2. Слой срезаемого сверлом материала

На каждый из этих участков приходится определенная доля в об-

щей величине крутящего момента и осевой силы. По эксперимен-

тальным данным [2], между этими составляющими существуют при-

мерно следующие закономерности:

0 2

2 1

1 3

2 0,08

;

2 0,57

2 0,8

;

2 0,4

2 0,12

;

2 0,03 ,

z z

M M

P P

M M

P P

M M

P P

−



⋅ ≈ ⋅





⋅ ≈ ⋅







⋅ ≈ ⋅





⋅ ≈ ⋅







⋅ ≈ ⋅





⋅ ≈ ⋅





(1)

где

0 2 2 1 1 3

2 , 2 , 2M M M

− − −

⋅ ⋅ ⋅

– крутящий момент на поперечной кром-

ке, на главных режущих кромках и на вспомогательных режущих

кромках соответственно;

0 2 2 1 1 3

2 , 2 , 2

z z z

P P P

− − −

⋅ ⋅ ⋅ – осевая сила на по-

перечной кромке, на главных режущих кромках и на вспомогатель-

ных режущих кромках соответственно;

– крутящий момент

и осевая сила, действующие на сверло.

Силы резания на главной режущей кромке

На инструмент в двухмерной эквивалентной системе передней

поверхности инструмента (рис. 3) действуют две силы: нормальная

сила F

и сила трения F

. F

действует по нормали к передней поверх-

ности инструмента, F

действует на передней поверхности инстру-

мента вдоль направления схода стружки.

Рис. 3. Плоская модель стружкообразования

Таким образом, две силы на передней поверхности и направление

схода стружки полностью определяют систему сил сверла, могут

быть взяты за основу при переходе к другим системам сил, в направ-

лении которых возможны экспериментальные измерения, а также

позволяют определить суммарную силу резания на кромке:

рез n f

F F F

= + . (2)

Поскольку процесс сверления осложнен не только различными

скоростями резания вдоль режущих кромок, отводом стружки и пр.,

но и геометрическими параметрами, изменяющимися вдоль главной

режущей кромки, разобьем главную режущую кромку сверла на эле-

ментарные участки, на каждый из которых действует элементарная

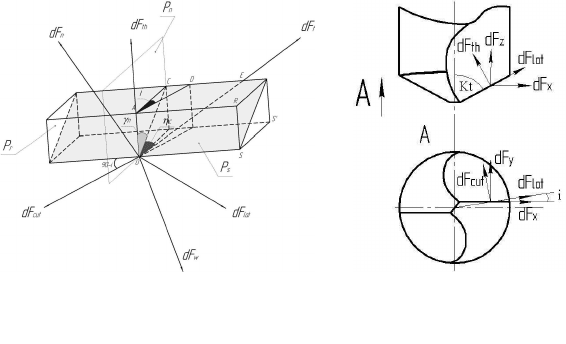
система сил (рис. 4).

Для перехода от направлений нормальной силы и силы трения

к направлениям тех сил, величины которых возможно измерить, не-

обходимо ввести три системы координат (рис. 4, б).

Первая система координат (СК) — СК передней поверхности

сверла

n f w

dF dF dF

, которая определяется направлениями элементар-

ной силы трения dF

, элементарной нормальной силы dF

и направ-

лением, перпендикулярным двум названным, dF

, в котором сила не

действует (|dF

|=0).

Рис. 4. Элементарный участок главной режущей кромки сверла (а)

и система элементарных сил, действующих на него (б)

Вторая СК – СК сверла

th cut lat

dF dF dF

– определяется как систе-

ма сил при косоугольном резании: элементарная осевая сила dF

элементарная сила резания dF

cut

и элементарная радиальная сила

lat

. Эти три компоненты силы могут быть выражены через эле-

ментарную нормальную силу и элементарную силу трения. Эле-

ментарная сила резания dF

cut

действует в направлении вектора

скорости резания V.

Направление элементарной косоугольной осевой силы dF

опре-

деляется векторным произведением единичных векторов в направле-

нии скорости резания и в направлении элемента режущей кромки,

т. е.

V L V L

× ×

. Направление элементарной радиальной силы dF

lat

определяется как

cut th cut th

dF dF dF dF

− × ×

Обе системы координат представлены на рис. 5.

Третья СК – базовая СК – определяется элементарной осевой силой

сверла dF

и элементарными радиальными силами dF

и dF

(рис. 6).

Величины сил |dF

|, |dF

| и |dF

| являются x, y, z – компонента-

ми результирующей трехмерной элементарной силы, действую-

щей на каждый элементарный участок. Элементарный момент

|dM

рассчитывается как произведение радиального расстояния до

рассматриваемого элементарного участка на элементарную силу

резания |dF

cut

Рис. 5. Системы координат

wfn

dFdFdF

latcutth

dFdFdF

в центре

элементарного участка главной режу-

щей кромки сверла

Рис. 6. Системы координат

latcutth

dFdFdF

ZYX

dFdFdF

Элементарные силы dF

, действующие в СК передней по-

верхности инструмента, можно представить в базовой СК

ZYX

dFdFdF

выразить через элементарную осевую силу сверла и элементарный

момент и, просуммировав данные величины всех элементарных уча-

стков вдоль режущей кромки, получить значения нормальной силы

резания F

и силы трения о переднюю поверхность F

Для этого необходимо осуществить переход от СК

n f w

dF dF dF

к СК

X Y Z

dF dF dF

в соответствии с представленными рис. 5 и 6. На рис. 5

изображен элемент косоугольного резания с углом наклона главной

режущей кромки i. СК передней поверхности

n f w

dF dF dF

соответствует

эффективной позиции резания. СК сверла

th cut lat

dF dF dF

представляет

элементарное косоугольное резание. Точка О является началом этих

систем координат и расположена в центре элемента режущей кромки.

Плоскость oce является передней поверхностью, P

(oars) – основной

плоскостью режущего инструмента, P

(oss) – инструментальной плос-

костью резания, P

(oac) – нормальной секущей плоскостью. Угол γ

(aoc) – нормальный передний угол, η

n f w

dF dF dF

(coe) – угол схода

стружки, i – угол наклона главной режущей кромки. Осуществим пере-

ход от СК к СК

th cut lat

dF dF dF

Для этого первую СК надо повернуть на

угол

вокруг оси