Jan Svoboda. Magnetic Techniques for the Treatment of Materials
Подождите немного. Документ загружается.

270 CHAPTER 4. DESIGN OF MAGNETIC SEPARATORS
Pole
Pole-piece
Coil
Yoke
L
g
Path of integration
B
A
C
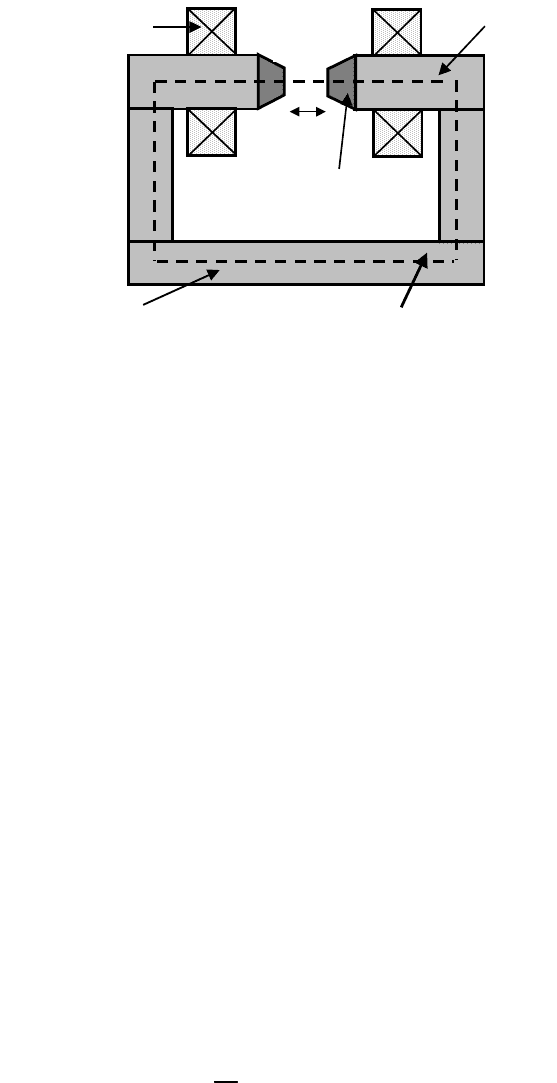
Figure 4.15: Schematic diagram of an electromagnet with iron yoke.
rare-earth magnets, with ( 100×10
8
m, pose a problem and a pulse width
of at least 10 ms must be used [P4].
4.3 Design of iron-core electromagnets
In section 1.7.2 the position of electromagnets with an iron yoke as a source
of magnetic field in magnetic separation was outlined. Although the iron-core
electromagnets have been recently replaced by rare-earth permanent magnets
in several types of magnetic separators, they still play an important role in
various designs of magnetic separators. In those applications where variable
magnetic field of moderate strength in a relatively large volume is required,
electromagnets with an iron yoke are the field source of choice.
In spite of availability of powerful modelling techniques for optimization of
electromagnet design, the initial design ought to be created based on experience
and, to some degree, on guesswork. In this section general principles of design
of electromagnetic circuits with an iron core will be described. The design of
such a circuit, schematically shown in Fig. 4.15, is governed by Ampere’s law
given by eq. (4.3). If we suppose that coils with a total number of turns Q are
wound onto the circuit, then Ampere’s law can be re-written as
I
F
K · g
o = QL (4.37)
The path of integration extends around the magnetic circuit as shown in Fig.
4.15. The magnetic induction E
j
in the air gap of length O
j
is, therefore, given
by
E
j
=
0
O
j
(QL
Z
EFD
Kgo) (4.38)

4.3. DESIGN OF IRON-CORE ELECTROMAGNETS 271
By calculating the actual field E inside the iron part of the circuit, we can
then determine the magnetic induction in the air gap from the value of the
magnetomotive force (or number of ampere-turns) QL=
We can define reluctances of the air gap
j
and of the iron part of the circuit
p
as
j
=
O
j
0
D
j
(4.39)
p
=
1
Z
EFD
go
D
p
(4.40)
where D
j
and D
p
are cross-sectional areas of the air gap and iron and is the
permeability of iron.
If the magnetization of the iron is much less than saturation, then AA
0
and
j
AA
p
= Then we have
E
0
=
0
QL
O
j
(4.41)
This equation expresses a linear relationship between E
0
and L,whichisob-
served for any type of electromagnet at low magnetic fields. If, however, the
magnetization of the iron approaches saturation, the permeability of the iron
is greatly reduced. Under these conditions eq. (4.41) is not valid and we must
use the following, more general equation to calculate E
j
E
j
=
QL
(
j
+
p
)D
j
(4.42)
For this purpose we must calculate
p
from eq. (4.40), which is a di!cult task
as we have no straightforward way of determining the value of as a function
of position o= Furthermore, the leakage of the flux will increase as becomes
small [I1].
4.3.1 Calculation of the magnetic field
The magnetic field produced in an air gap of an electromagnet can be calculated
by integrating contributions of the magnetic charges on the pole surface. For
cylindrical flat poles, as shown in Fig. 4.16, the magnetic induction in the gap
is given by [M21]
E
j
= M
v
f
(1 cos )=M
v
f
·
1
{
(u
2
2
+ {
2
)
1@2
¸
(4.43)
where
f
is a correction factor.
For tapered poles with coinciding apexes (Fig. 4.16) the magnetic induction
becomes
E
j
= M
v
f
(1 cos +cos sin
2
ln
u
2
u
1
)= (4.44)
M
v
f
·
1
{
(u
2
1
+ {
2
)
1@2
+
{u
2
1
(u
2
1
+ {
2
)
2@3
ln
u
2
u
1
¸
(4.45)
272 CHAPTER 4. DESIGN OF MAGNETIC SEPARATORS
L
p
x
r
2
ș
ș
r
1
r
2
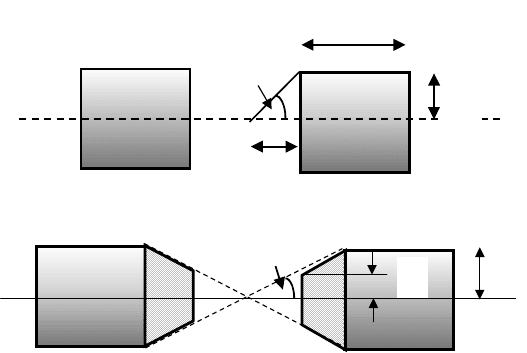
Figure 4.16: Cylindrical flat poles and tapered poles with coinciding apexes.
It can be seen that in this case the magnetic induction consists of two terms, the
first term being the magnetic induction for cylindrical flat poles. The second
term is greater than zero (provided that ?90
0
and u
2
Au
1
), and magnetic
induction generated by tapered poles, therefore, generates a greater magnetic
field than flat poles. This second term achieves its maximum for = 54.7
0
.
It was shown by Montgomery [M21] that eq. (4.43) gives good results if
f
=
0=7 for 1, while for
=
0=5 the correction factor
f
=1gives a good
agreement between calculated and measured values of magnetic induction.
is a geometrical factor defined as = O
s
@2u
2
and O
s
is defined in Fig. 4.16. In
magnets with tapered pole-pieces eq. (4.45) has very good predictive capability
for
f
=
1.
4.3.2 Shape of iron parts of the circuit
The yoke, as shown in Fig. 4.15, serves to transport the magnetic flux from
the end of one pole to the end of the other pole. The presence of iron permits
useful values of the magnetic induction (for example, up to 2 T) to be reached
with modest investments in ampere-turns. The iron yoke also confines the stray
flux to the immediate vicinity of the magnet gap. The yoke should, therefore,
have reasonably high permeability, even when the poles and pole pieces are
saturated. Since the magnetization curve of soft iron has a knee at M@M
v
= 70%
to 80%, it is recommended to make the cross section of the yoke about 1.2 to
1.4 times that of the poles [I1]. In modern magnets the yokes and the poles are
made of laminations.
In order to attain the strongest possible magnetic field, the shape of the poles
and pole pieces must be determined to satisfy the following two requirements:
4.3. DESIGN OF IRON-CORE ELECTROMAGNETS 273
x
1
x
2
r
2
r
3
r
1
ș
2
x
3
ș
1
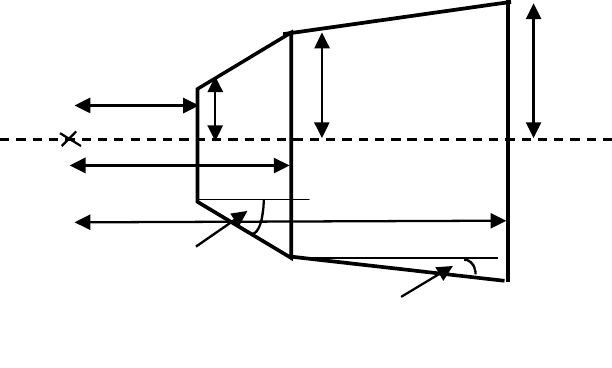
Figure 4.17: Shape of a pole with two conical pole-pieces.
(a) The magnetization of the poles and pole pieces must produce the maxi-
mum possible field when they are saturated.
(b) Saturation should be achieved simultaneously throughout the volume of
the poles and the pole pieces.
In view of increasing leakage from the poles, as their magnetization ap-
proaches saturation, the cross-section of the poles must be reduced as the tip of
the pole is approached. The flux density will thus be maintained constant and
the requirement (b) will be met.
In order to satisfy the requirement (a), Ewing [E2] showed, as early as the
end of the nineteenth century, that the shapes of the pole pieces must be conical,
preferably with the vortex angle of 54.7
0
. In an actual electromagnet, however,
this conical shape must be modified, in order to secure homogeneity of the field
in the air gap and to ensure that permeability is constant throughout the pole
and the pole piece [I2].
Analyzing eqs. (4.43) and (4.45), Ishikawa and Chikazumi [I2] showed that
the pole shape that satisfies the above requirements can be approximated by
the shape shown in Fig. 4.17. This shape is composed of a pole-tip of radius
u
1
, a conical part of radius u
2
and another conical part of radius u
3
. Analysis
of this shape indicates that that the maximum field in the air gap depends
on the value of u
2
@{
1
and not on u
1
@{
1
> while the homogeneity of the field
is determined by the value of u
1
@{
1
. The issue of the field homogeneity is
not critically important in magnetic separation and the parameter u
1
@{
1
is,
therefore, of limited relevance for the design of a circuit of a magnetic separator.
274 CHAPTER 4. DESIGN OF MAGNETIC SEPARATORS
A
B
C
B
0
NI
(NI)
A
(NI)
c
(NI)
B
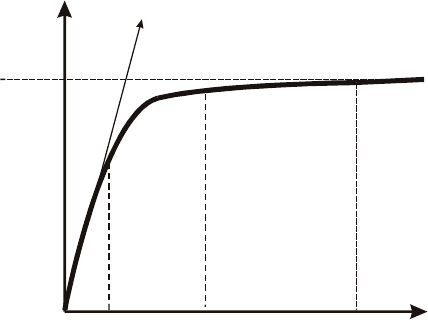
Figure 4.18: The excitation curve of an electromagnet showing the unsaturated
zone (A), transition zone (B) and saturated zone (C).
4.3.3 Practical procedure for design of the poles
The design of an electromagnet for a magnetic separator is based on two fun-
damental specifications, namely the required magnetic field strength E
j
and
the length (2{
1
) and the depth (2u
1
) of the air gap. The former parameter is
determined by the required separation e!ciency while the latter mainly by the
desired throughput of the separator. In wet high intensity magnetic separators
the depth of the air gap determines the depth of the matrix bed, which in turn
also aects the eectiveness of separation.
From an economic point of view, the size and thus the price of the magnet
depends strongly on the length of the air gap O
j
=2{
1
= The volume of the
magnet is approximately proportional to (2{
1
)
3
.
Contribution of iron to the magnetic field
The contribution of the iron circuit to the magnetic induction in the air gap
can be divided into three regions, as illustrated by the excitation curve shown
in Fig. 4.18. In the unsaturated zone D the reluctance of the air gap is much
greater than the reluctance of the rest of the circuit so that almost the entire
magnetomotive force appears across the gap. Once the transition zone sets in,
the flux that reaches the air gap is reduced. In order to achieved the desired
magnetic induction, the number of ampere-turns must be increased, as shown
in Fig. 4.18.
It was reported by Montgomery [M21] that usually (QL)
E
@(QL)
D
1.1 at
60% of the maximum magnetic field, while a typical value of this ratio at 85%
of the maximum field is about 2. A plot of this ratio against the percentage

4.3. DESIGN OF IRON-CORE ELECTROMAGNETS 275
Figure 4.19: Ampere-turns needed to achieve a required magnetic field.
of the maximum induction, for a typical magnet, is shown in Fig. 4.19. With
the number of ampere-turns known at 60% and 85% of the maximum field, a
satisfactory curve can be drawn representing the magnetization of iron from 0 to
100% [M21]. Figure 4.20 shows the number of ampere-turns required to obtain
85% of the maximum field, as a function of the geometry of the magnet.
Design of coils
Coils in an iron-core electromagnet serve two functions: they provide the elec-
tromagnetic force to magnetize the iron, and they contribute a certain magnetic
field in the air gap. The magnetic induction generated by a coil, the geometry
of which is shown in Fig. 4.21, at the centre of the coil, is given by [M22]:
E
j
=
QL
2
0
d
1
( 1)
I (> ) (4.46)
where = d
2
@d
1
, = e@d
1
and I (> ) is the field factor defined (in SI units)
as
I (> )= ln
+(
2
+
2
)
1@2
1+(1+
2
)
1@2
(4.47)
The field along the axis } of a coil of axially uniform excitation can be written
[M22]:
E
}
(
}
d
1
)=E
}
(0)
·
I (> + }@d
1
)+I(> }@d
1
)
2I (> )
¸
(4.48)

276 CHAPTER 4. DESIGN OF MAGNETIC SEPARATORS
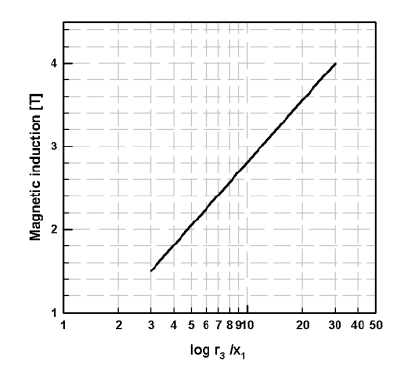
Figure 4.20: Ampere-turns required to reach 85% of the maximum magnetic
field in the air gap, as a function of the ratio of the pole face
diameter and the gap length, u
1
/{
1
, for several u
3
@u
1
ratios (adapted
from [M21]).
z
a
1
a
2
2b
Figure 4.21: Definition of geometrical parameters of a solenoid coil.
4.3. DESIGN OF IRON-CORE ELECTROMAGNETS 277
Figure 4.22: Empirically obtained curve expressing the maximum magnetic field
as a function of ratio of the pole diameter to air gap length (adapted
from [I1]).
If the point at which this field is measured lies outside the coil (e.g. in the air
gap of an electromagnet) the following relationship should be used in eq. (4.48):
I (> }@d
1
)=I (> }@d
1
) (4.49)
Practical rules for the design
Taking into account the above analysis, the following rules should be followed
in the design of an electromagnet:
(1) Although the field homogeneity is not critical in magnetic separation,
a suitable choice of the pole radius u
1
,insuchawaythatu
1
=2{
1
, usually
ensures the field homogeneity within 10
3
=
(2) The maximum magnetic field is a function of the maximum pole diameter
2u
3
, irrespective of dierences in pole shapes [I1]. Using Figs. 4.20 and 4.22,
approximate value of the maximum diameter of the pole from the selected values
of E
j
and {
1
can be determined.
(3) The optimum value of angle
1
depends on the value of u
1
@{
1
which
again is not of major importance in magnetic separators.
1
usually ranges from
50
0
to 60
0
.
(4) A generally accepted rule is that u
3
= 1.2u
2
to 1.4u
2
=
(5) The number of ampere-turns should be selected in such a way that
(QL)
E
=1=1(QL)
D
or 2(QL)
D
, if 60% or 85% of the maximum field is to be
achieved, respectively.
Figure 4.23 illustrates modelling of the magnetic flux in a iron-core electro-
magnet.
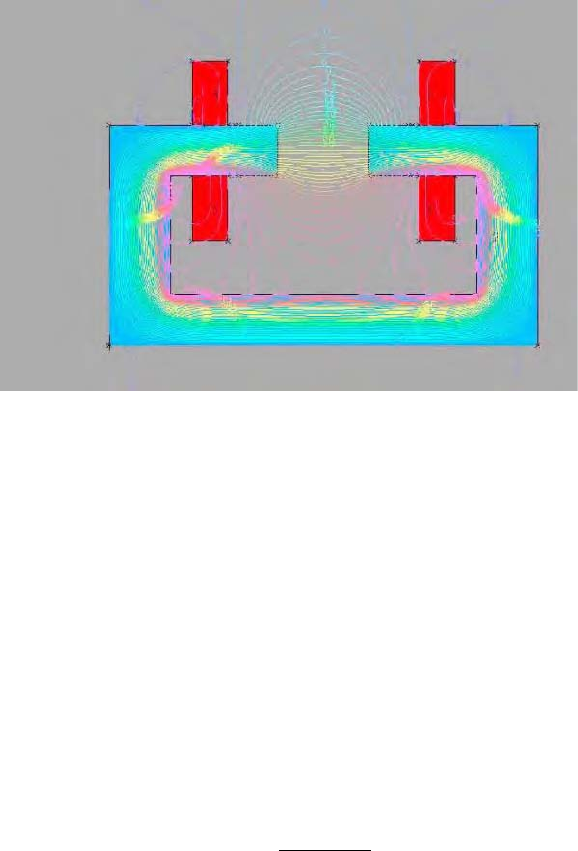
278 CHAPTER 4. DESIGN OF MAGNETIC SEPARATORS
Figure 4.23: Modelling of an iron-core electromagnet.
4.4 Design of solenoid magnets
As has already been discussed in Section 1.7.3, generation of magnetic induction
by iron-core electromagnets is limited by the saturation of the iron. In order to
overcome this limitation, Bitter [B24] proposed the use of a magnetizing solenoid
surrounded by steel cladding. The magnetic induction in the working volume
of such a magnet is given by the sum of the contribution from the coil and
from the magnetized iron, as expressed by eq. (1.50). Figure 1.40 illustrates the
relative contributions from these two components of the magnet.
The idealized circuit of the iron-clad solenoid is shown in Fig. 4.24. The
magnetic induction in the air gap is given by Ampere’s law (eq. (4.41)). If the
magnetic reluctance of the iron frame cannot be neglected, eq. (4.42) must be
used. In a more practical form, a leakage factor N canbeincludedineq. (4.42),
and we can write:
E
j
=
0
QL
O
j
(1 + N)
(4.50)
The leakage factor N is often taken equal to 0.2 [T6, M23].
It transpires from eq. (4.50) that the number of ampere-turns required to
generate a given magnetic induction is determined solely by the length of the
field (or the length of the air gap) O
j
and is independent of the radius d
1
of
the working volume. Solenoids shown in Fig. 4.25 have the same length of the
air gap, while their radii dier, and the number of ampere-turns required to
generate a required magnetic induction is the same for both solenoids. This
feature is extremely useful in the scale-up of magnetic separators. In iron-core
electromagnets a higher throughput of separators is achieved by increasing the

4.4. DESIGN OF SOLENOID MAGNETS 279
L
g
a
1
a
2
t
Figure 4.24: Schematic diagram of an iron-clad solenoid.
length of the air gap. This requires an increased number of ampere-turns, as
follows from eq. (4.41). This, in turn, results in an increase in the mass, size
and cost the magnet.
On the other hand, the scale-up of a magnetic separator based on an iron-
clad solenoid is achieved by increasing the diameter of the solenoid, keeping the
length of the air gap constant. The number of ampere-turns will be constant,
only the length of the conductor, and thus its resistance will increase.
L
g
2a
1
Figure 4.25: Two iron-clad solenoids having the same length of the air gap and
dierent radii.
