Jan Svoboda. Magnetic Techniques for the Treatment of Materials

Подождите немного. Документ загружается.

240 CHAPT ER 3. THEORY OF MAGNETIC SEPARATION

pmb

net

Rotatin

ferrofluid

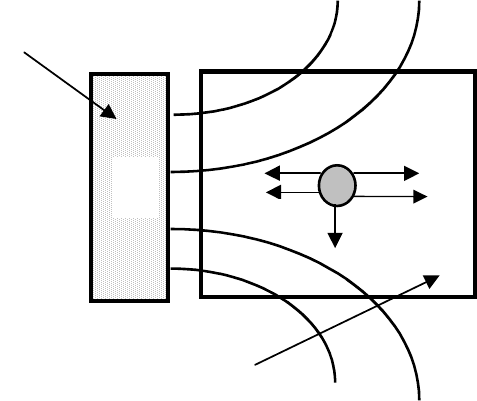
Figure 3.65: Forces acting on a particle in a rotating ferroﬂuid in a non-

homogeneous external magnetic ﬁeld.

3.8.6 Separation in a rotating ferroﬂuid

In order to overcome certain practical limitations of gravity-based ferrohydro-

static separation, particularly treatment of ﬁne particles, several proposals were

made [R11, A14, W7] to replace the force of gravity by the centrifugal force.

Work carried out at Intermagnetic Corp.(USA) in early nineteen eighties re-

sulted in a new rotation-based separation process called Magstream.

The theory and the practice of separation in a rotating ferroﬂuid have been

described in several publications [W20, W21, W22, B22, B23, S44]. Forces act-

ing on a particle suspended in a rotating ferroﬂuid exposed to a non-homogeneous

magnetic ﬁeld are illustrated in Fig. 3.65. Walker and Devernoe [W22] assumed

that the axis of the separator was vertical and ignored the force of gravity and

the hydrodynamic drag acting on the particle. In this scenario only the radi-

ally outward centrifugal force I

, magnetic traction force I

and the inward

buoyancy force I

spe

resulting from the outward attraction of the magnetic ﬂuid

by the magnetic ﬁeld were included. The centrifugal force can be written

= Y

(

 

u (3.171)

where u is the radial position of the particle and $ is the rotational velocity of

the ferroﬂuid. The magnetic buoyancy force is given by eq. (3.150) while the

magnetic traction force is given by eq. (3.148).

The total force I

acting on a particle in the horizontal direction, along the

3.8. SEPARATION IN MAGNETIC FLUIDS 241

radius of the rotating device, can be expressed as:

= Y

(

 

u +





EuE 



uE (3.172)

In equilibrium I

= 0 and the cut-point density for non-magnetic particles

(

= 0) can be determined from the above equation as:



= 

uE (3.173)

where Q is the number of revolutions of the rotating device per minute (Q

=60$/2), and N is a parameter determined by the design of the magnetic

system of the rotating separator:

N =15



1@2

(3.174)

Equation (3.173) is used to calculate the operating conditions in the Magstream

separator [W22]. It is apparent from eqs. (3.173) and (3.174) that if the pattern

of the magnetic ﬁeld is designed in such a way that the ﬁeld gradient is a linear

function of the radial position u,thenN = const. and the cut-point density is

determined solely by the polarization and the rotational velocity of the ferroﬂuid.

This condition is satisﬁed, for instance, for the magnetic ﬁeld generated by a

sextupole magnet, such that the ﬁeld magnitude is given by E = E

(u@u

)

q1

where 2q =6,andE

is the magnetic induction at u

, the outside wall of the

separation annulus [W20].

Equation (3.173) is equivalent to eq. (3.154) derived for ferrohydrostatic

separation. It can, therefore, be seen that the cut-point density in a rotating

ferroﬂuid can be controlled, in a wide range, by varying the rotational velocity

and the ﬁeld gradient. The operating density range of the ﬂuid in a ferrohydro-

static separator is, in contrast, controlled by adjusting the ﬁeld gradient only.

However, in most Magstream models the magnetic ﬁeld is generated by per-

manent magnets and the ﬁeld gradient is given by the design of the magnetic

system. For instance, in Magstream Model 200 the ﬁeld gradient is equal to

uE = 13.2u T/m (1320u G/cm).

Simplifying assumptions introduced by Walker and Devernoe [W22], when

deriving eq. (3.173), reﬂect themselves in limited accuracy of determination of

the cut-point density and thus in reduced e!ciency of separation. Bunge and

Fuerstenau [B22], in order to account for the dispersion component of particle

behaviour, developed a diusion model of separation. They concluded that the

primary cause of non-ideal separation in a rotating ferroﬂuid is the dispersion

of the settling particles. This fuzzy behaviour was ascribed to the eect of tur-

bulence, particle shape and interparticle interactions. The model of Bunge and

Fuerstenau, however, was not able to explain the dependence of the separation

e!ciency on particle size and ﬂuid viscosity [B22, B23].

242 CHAPT ER 3. THEORY OF MAGNETIC SEPARATION

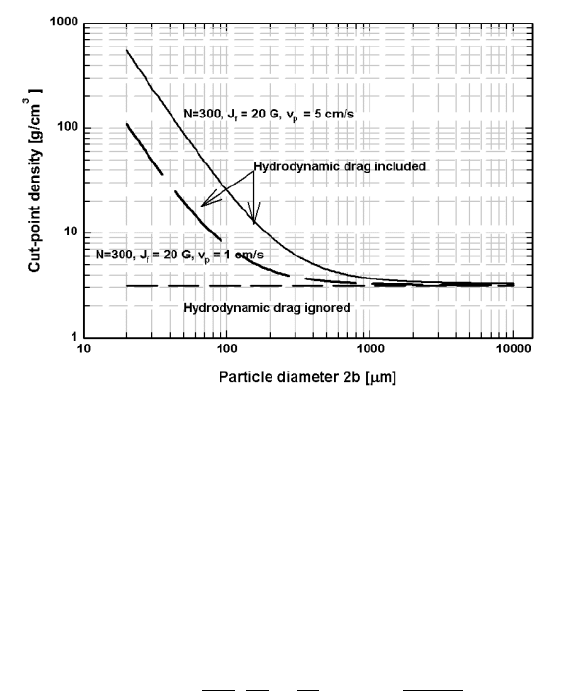
Figure 3.66: The cut-point density of non-magnetic particles in Magstream, as

afunctionofdensity.u = 2.1 cm,  =5×10

3

Pa×s, 

(no drag)

= 3130 kg/m

(adapted from [S44]).

Svoboda [S44] included the horizontal hydrodynamic drag (eq. (1.16)) into

the balance of forces and obtained, for the cut-point density,



= 

(









E)uE +

9y

(3.175)

This more general expression shows that the hydrodynamic interaction of parti-

cles with the ferroﬂuid contributes to the determination of the cut-point density.

The most signiﬁcant consequence of the hydrodynamic contribution is that the

cut-point density depends on particle size, in contrast to eq. (3.173). It tran-

spires from eq. (3.175) that the correction hydrodynamic term gains importance

for weakly magnetic and/or highly viscous ferroﬂuids (low M

and high ), and

for small particles. In addition, the hydrodynamic term depends on the position

of a particle within the separation space.

The eect of particle size on the cut-point density of non-magnetic particles

is illustrated in Fig. 3.66. It can be seen, for example, that a cut-point density of

3130 kg/m

, determined by ignoring the hydrodynamic drag, is accurate down

to particle size of 2 mm. For particle diameters smaller than 2 mm the relative

importance of the hydrodynamic interaction steeply increases and separation

becomes inaccurate.

3.9. EDDY-CURRENT SEPARATION 243

3.9 Eddy-current separation

It has been stated in Section 2.7 that when conducting particles move through

a region of spatially varying magnetic ﬁeld, then an electromagnetic force, and

hence eddy currents, are induced in such particles. The eddy currents are caused

by time-dependent changes of the magnetic induction acting on a particle and

are given by the Faraday induction law:



u ×



m = 



(3.176)

where m is the current density and 

is the speciﬁc electrical conductivity of

the particle.

These eddy currents generate a magnetic ﬁeld opposed to the external mag-

netic ﬁeld. This opposite ﬁeld then produces a repulsive Lorentz force on a

linear element gv of the conductor [S47]



= Lgv ×



E (3.177)

where L is the current carried by the conductor.

This force can be made lateral to the motion of the particles and so to

deﬂect them. Negligible eddy currents develop in non-conducting elements,

which, therefore, experience no deﬂection. In this way it is possible to separate

conducting particles from non-conducting and this method has been developed

into an e!cient technique for the recovery of non-ferrous metals from streams

of industrial or municipal waste.

The varying magnetic ﬁelds can be generated in several ways. In linear

motors, the magnetic ﬁelds are generated by electromagnets with alternating

currents. The repulsive force can also be generated by moving particles through

a non-homogeneous static or rotating magnetic ﬁelds. These ﬁelds can be con-

veniently generated by permanent magnets.

3.9.1 Static ramp eddy-current separator.

The simplest design of an eddy-current separator (ECS) proposed by Schloe-

mann [S45] comprises a long ramp, as shown in Fig. 3.67. The ramp consists

of permanent magnet strips of alternating polarity, mounted on a mild steel

base plate inclined at an angle of about 45

to the ramp axis. A stream of

particles is allowed to slide down the ramp. The non-conducting particles are

not aected by the magnetic ﬁeld and travel straight down the ramp. The

conducting particles, under the inﬂuence of the eddy-current-induced repulsive

Lorentz force perpendicular to the magnet strips, are deﬂected from the stream

of non-conducting particles, as shown in Fig. 3.67. The magnitude of the lateral

deﬂection depends, among other things, on the electrical conductivity, density,

size and shape of the particles and the strength and the periodicity of the mag-

netic ﬁeld.

244 CHAPT ER 3. THEORY OF MAGNETIC SEPARATION

Magnet strips

alternating

polarity

Non-conducting

particles

Conducting

particles

Feed

Mild steel

base

Figure 3.67: Schematic diagram of a ramp eddy-current separator (adapted from

Schloemann [S45]).

Schloemann [S45] found that the component of the repulsive force in |-

direction acting on a conducting particle is given by:

= p

{

(3.178)

where p

and y

{

are the mass and velocity in the { - direction of the particle,

respectively. The coe!cient  is a function of particle shape, and for a thin disc

of diameter g

, it is given by [S45]:

 =





(

}

)

(3.179)

and approximate expression for the repulsive force (eq. (2.6)) is quoted by

Schubert [S22]:

' p





{

(3.180)

where i is the period of the magnetic ﬁeld. This equation, supported by ad-

ditional calculations of the repulsive force on particles of various shapes [S46,

V3, V4] shows that the repulsion force is a function of the material parameter



@

, given in Table 2.1, and of the square of the magnetic induction.

Schloemann [S45] calculated trajectories of disc-shaped particles in a ramp

eddy-current separator from the following equations of motion:

{

= j sin  and

= y

{

(3.181)

3.9. EDDY-CURRENT SEPARATION 245

It follows from eqs. (3.181) that

{(w)=

j sin  + y

w (3.182)

|(w)=(

j sin  +

) (3.183)

where y

{

(0) = y

The particle trajectory, in a frictionless situation, is then:

|({)=



{

3@2

(j sin )

1@2

1  2

{

´³

{

1@2

{

3@2

(3.184)

where {

is the distance along the ramp after which a particle starting at rest

has attained the velocity y

= Therefore, {

= y

@2j sin . A more detailed

analysis of the eect of friction on particle motion can be found in [S45].

Although ramp eddy-current separators were used in several industrial in-

stallations [S46], their commercial success was limited. Poor selectivity, partic-

ularly for small particles, and low throughput were responsible for the failure of

ramp separators to ﬁnd a long-term production application.

Further development of the ramp concept resulted in the design of a vertical

eddy-current separator [V4, V3], in which the deﬂection occurred in a vertical

channel between two arrays of magnet strips mounted on the inside of two

vertical parallel mild steel plates. The strips of alternating polarity were also

oriented at an angle to the base plate and, in addition, the magnets on the

opposite plate were also arranged with opposite polarity. These static gravity-

based separators also failed to gain industrial acceptance and were replaced by

dynamic rotating drum eddy-current separators.

A detailed study of the separating Lorentz force, by eliminating the compet-

ing forces such as gravity and frictional forces, was conducted theoretically by

Fletcher et al. [F15, F16, F17]. These idealized physical models of separation of

conducting and non-conducting elements moving in a horizontal plane and inci-

dent on a single boundary of a semi-inﬁnite magnetic ﬁeld were compared with

the experimental results. Theoretical trends of the metal recovery with par-

ticle size, splitter position and boundary ﬁeld proﬁle were in good agreement

with experimental observations. Although the ﬁeld geometry and the separation

arrangement in these studies diered from those used in practical applications,

the methodology used can serve as a starting point for more fundamental re-

search into the mechanisms of eddy-current separation.

3.9.2 Rotating drum eddy-current separators

Presently, the eddy-current separators most frequently used in industrial prac-

tice are based on a rotating drum concept. The active part of such a separator

is a drum containing rapidly rotating magnetic system. Permanent magnets

are arranged, with alternating polarity, along the circumference of the magnetic

system. This concept is schematically described in Figs. 2.100 and 3.68.

246 CHAPT ER 3. THEORY OF MAGNETIC SEPARATION

SSSNNN

Belt

Drum rotation

Eddy current

Lorentz

force

Particle

Figure 3.68: A top view of an eddy-current separator based on a rotating drum.

The particles are expelled by the Lorentz force in the direction of

the direction of drum rotation (adapted from [R17]).

In order to calculate the forces acting on particles due to eddy current, a

dipole model was developed by Rem et al. [R17, R18]. It was assumed that the

magnetic ﬁeld induces eddy currents within a particle, which in turn generate

a magnetic moment in that particle. The interaction between the magnetic

moment 

and the external magnetic ﬁeld E results in eddy current forces.

The force can then be expressed as:



= 

uE (3.185)

where 

= P

. The torque on the particle is given by eq. (3.48).

In order to determine the force acting on a particle, given by eq. (3.185),

a magnetic ﬁeld generated by the magnetic system must be calculated. Rem

et al. [R17] have shown that the components of the magnetic induction in the

cylindrical coordinate system (u> !> }) relative to the drum axis can be written:

q=0

(u@U

guxp

)

(2q+1)n1

sin[(2q +1)n(!  $

guxp

w)] (3.186)

q=0

e

(u@U

guxp

)

(2q+1)n1

cos[(2q +1)n(!  $

guxp

w)] (3.187)

where e

are the Fourier coe!cients, U

guxp

the radius of the drum, n the number

of pairs of the magnets used in the drum and $

guxp

the angular velocity of the

drum. The Fourier coe!cients can be determined by measuring the magnetic

ﬁeld strength as a function of distance from the magnetic pole surface.

Based on eqs. (3.186) and (3.187), Zhang et al. [Z4] obtained the following

expressions for the tangential I

and radial I

eddy-current forces acting on

the particle:

Osw

2vY



(n$

guxp

+ )

1+(n$

guxp

+ )



(3.188)

3.9. EDDY-CURRENT SEPARATION 247

Osu

2vY



(n$

guxp

+ )



1+(n$

guxp

+ )



(3.189)

where z is the width of one pair of magnets, v is the shape factor of the particle

and  is the angular velocity of particle rotation.  is a characteristic time with

which the induced magnetic ﬁeld decays in the particle given by [Z4]:

 = 



(3.190)

where e is the particle radius.

The torque on the particle was found to be [Z4]:

W =



(n$

guxp

+ )

1+(n$

guxp

+ )



(3.191)

It can be seen that the eddy-current forces and the torque depend on the square

of the magnetic ﬁeld strength. By replacing ceramic ferrite permanent magnets

by rare-earth magnets, a considerable increase in the separating force can be,

therefore, achieved.

Competing forces

Gravitational, centrifugal, frictional and aerodynamic forces compete with eddy-

current forces and their relationship determines the particle trajectories in an

eddy-current separator. Eddy current forces and a wide spectrum of compet-

ing forces and their various dependencies on particle size and shape, electrical

conductivity, magnetic ﬁeld strength and its frequency (or the angular velocity

of the rotating drum) make the determination of particle trajectories and thus

the e!ciency of separation a problem of considerable complexity. Only rudi-

mentary eorts have been made the develop the balance of forces in a rotating

drum eddy-current separator [Z4, R17, R18].

Rem et al. [R18] developed a model for simulation of such a rotating drum

ECS. The eddy-current forces and some of the competing forces were included in

the model and particle trajectories were calculated. Typical trajectories, shown

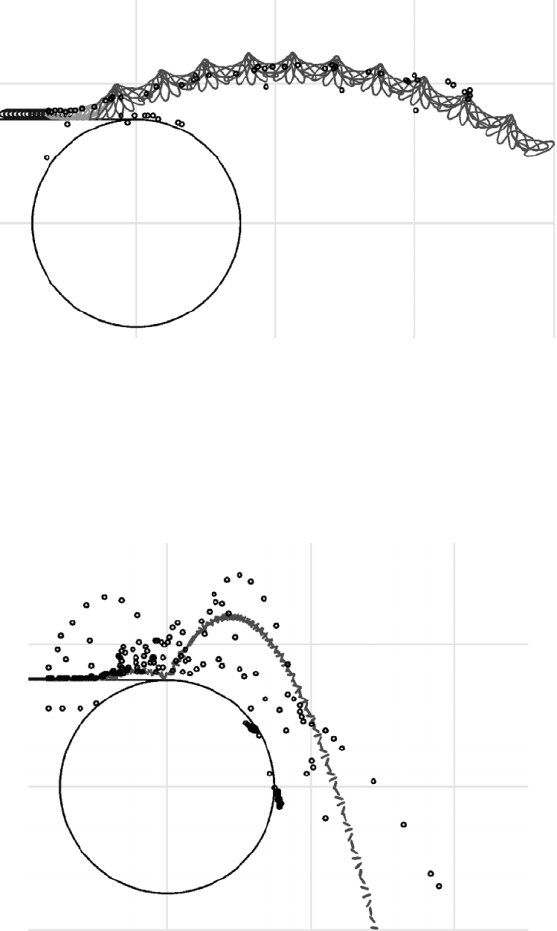
in Figs. 3.69 and 3.70, comprise the rolling, sliding and ﬁnally ﬂying stages. It

can be seen that at low belt velocities (Fig. 3.70) light particles tend to lose

contact with the belt at an early stage and they collide with the belt at a later

stage.

As a result of the dependence of the eddy-current forces and other forces

on the cube of the particle size, the particle size is the most signiﬁcant variable

aecting the performance of a separator. It transpires from the above equations

that also the particle shape plays an important role in the separation process.

For instance, it was observed that ﬂat particles exhibit much greater displace-

ment by eddy-current forces than spherical particles. In spite of considerable

complexity of the process, some general rules that govern the e!ciency of sep-

aration in a drum ECS can be formulated. In order to achieve a high recovery

of conducting particles, the eddy-current separating force must be greater than

248 CHAPT ER 3. THEORY OF MAGNETIC SEPARATION

Figure 3.69: Particle trajectories in a rotating drum ECS. Three stages of par-

ticle motion, namely rolling, sliding and ﬂying are apparent. Op-

erating conditions: belt speed: 1.5 m/s, drum angular velocity: 35

1

, material: aluminium particles 15 mm in diameter, 45 mm long

(courtesy of P.C. Rem).

Figure 3.70: Particle trajectories in a rotating drum ECS, at low belt velocity.

Belt speed: 0.5 m/s, drum angular velocity: 35 s

1

, material: alu-

minium particles of diameter of 10 mm, 2 mm thick (courtesy of

P.C. Rem).

3.9. EDDY-CURRENT SEPARATION 249

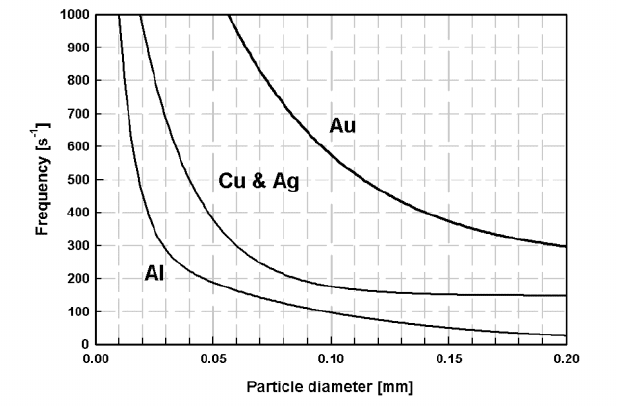
Figure 3.71: Frequencies required to rotate metal particles of various diameters

(adapted from Allen [A21]).

the sum of the competing forces:

vhsdu

frps

(3.192)

If, however, I

vhsdu

AA I

frp

, selectivity of separation will be low, as no dis-

tinction will be made between various classes of conducting particles. Selective

separation of one metal from another is determined by the interplay between

corresponding eddy-current and competing forces. Selective separation of metal

(1) from metal (2) will be achieved when the following relationship is met:

(1)

vhsdu

frps

(2)

vhsdu

(3.193)

However, when I

vhsdu

frps

, no separation based on the characteristic prop-

erty, such as electrical conductivity in ECS, will take place.

3.9.3 Eddy-current separation by particle rotation

With decreasing particle size, the torque on the particle become an important

separating force. Also, when the particle size becomes much smaller than the

width of the magnet strips used in the rotating drum eddy-current separators,

the particles increasingly respond to the ﬁeld changes by rotation rather than

by repulsion [A21]. As a result of decrease in the particle throw and increase

of particle rotation as particle size decreases, Allen [A21, A22] proposed to use

particle rotation as the separating mechanism of conducting particles.