Jacques I. Mathematics for Economics and Business
Подождите немного. Документ загружается.


7 Verify that the points (0, b) and (1, a + b) lie on the line
y = ax + b
Hence show that this line has slope a.
8 Sketch the graph of the function
f(x) = 5
Explain why it follows from this that
f ′(x) = 0
9 Differentiate the function
f(x) = x
7
Hence calculate the slope of the graph of
y = x
7
at the point x = 2.
10 Differentiate
(a)
y = x
8
(b) y = x
50
(c) y = x
19
(d) y = x
999
11 Differentiate the following functions, giving your answer in a similar form, without negative or frac-
tional indices.
(a)
f(x) = (b) f(x) =
3
x (c) f(x) = (d) y = xx
12 Complete the following table of function values for the function, f(x) = x
2
− 2x:
x −1 −0.5 0 0.5 1 1.5 2 2.5
x
2
− 2x
Sketch the graph of this function and, by measuring the slope of this graph, estimate
(a)
f ′(−0.5) (b) f ′(1) (c) f ′(1.5)
13 For each of the graphs
(a)
y = x (b) y = xx (c) y =
A is the point where x = 4, and B is the point where x = 4.1. In each case find
(i) the y coordinates of A and B.
(ii) the gradient of the chord AB
(iii) the value of at A.
Compare your answers to parts (ii) and (iii).
14 Find the coordinates of the point(s) at which the curve has the specified gradient.
(a)
y = x
2/3
, gradient = 1/3 (b) y = x
5
, gradient = 405
(c) y = , gradient = 16 (d) y = , gradient =−
3
64
1
x
x
1
x
2
dy
dx
1
x
1
4
x
1
x
3
Differentiation
250
MFE_C04a.qxd 16/12/2005 11:09 Page 250

section 4.2
Rules of differentiation
Objectives
At the end of this section you should be able to:
Use the constant rule to differentiate a function of the form cf(x).
Use the sum rule to differentiate a function of the form f(x) + g(x).
Use the difference rule to differentiate a function of the form f(x) − g(x).
Evaluate and interpret second-order derivatives.
Advice
In this section we consider three elementary rules of differentiation. Subsequent sections
of this chapter describe various applications to economics. However, before you can tackle
these successfully, you must have a thorough grasp of the basic techniques involved.
The problems in this section are repetitive in nature. This is deliberate. Although the rules
themselves are straightforward, it is necessary for you to practise them over and over again
before you can become proficient in using them. In fact, you will not be able to get much
further with the rest of this book until you have mastered the rules of this section.
Rule 1 The constant rule
If h(x) = cf (x) then h′(x) = cf ′(x)
for any constant c.
This rule tells you how to find the derivative of a constant multiple of a function:
differentiate the function and multiply by the constant
MFE_C04b.qxd 16/12/2005 11:11 Page 251

Differentiation
252
Example
Differentiate
(a) y = 2x
4
(b) y = 10x
Solution
(a) To differentiate 2x
4
we first differentiate x
4
to get 4x
3
and then multiply by 2. Hence
if y = 2x
4
then = 2(4x
3
) = 8x
3
(b) To differentiate 10x we first differentiate x to get 1 and then multiply by 10. Hence
if y = 10x then = 10(1) = 10
dy
dx
dy
dx
Practice Problem
1 Differentiate
(a)
y = 4x
3
(b) y = 2/x
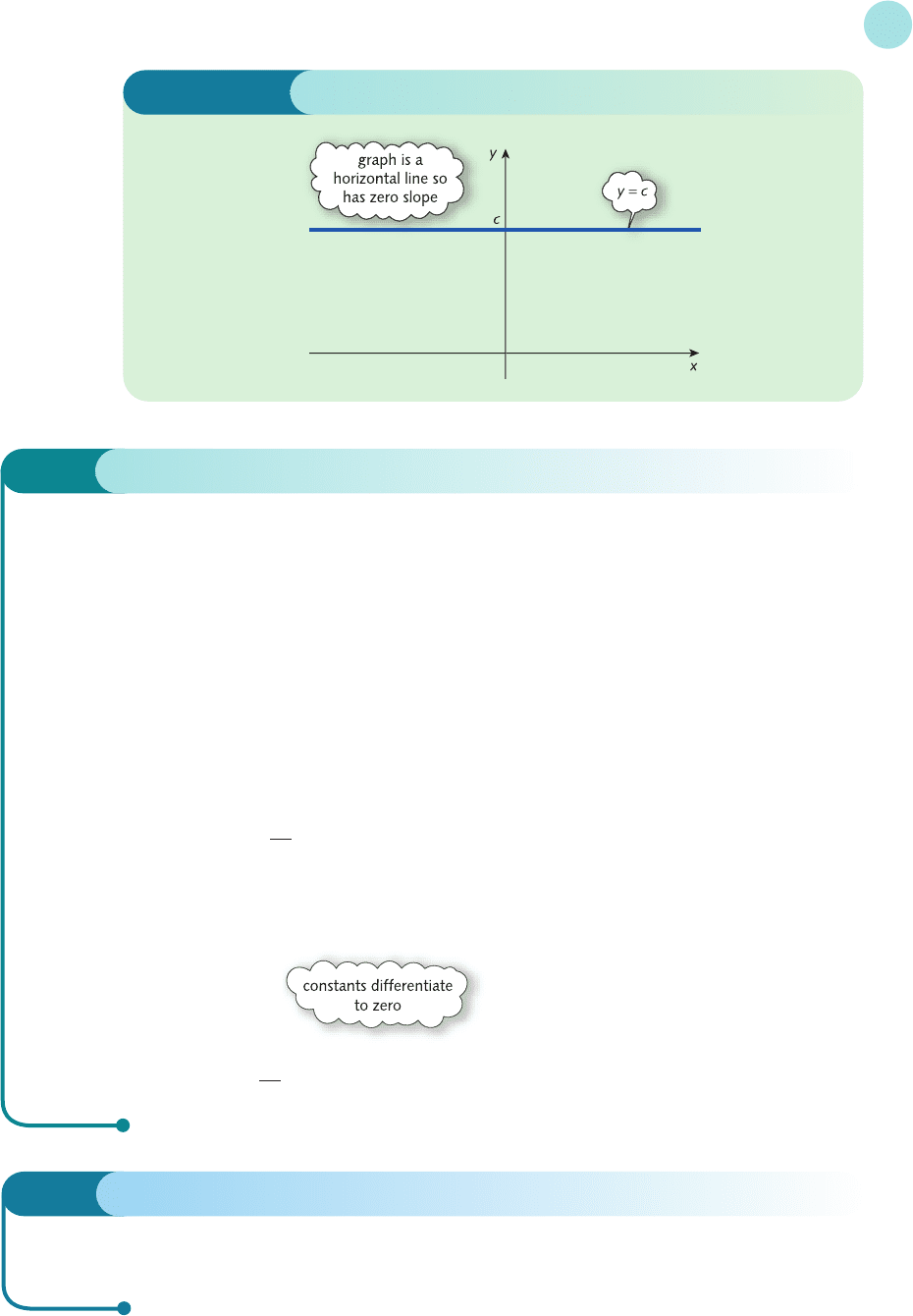
The constant rule can be used to show that
constants differentiate to zero
To see this, note that the equation
y = c
is the same as
y = cx
0
because x
0
= 1. By the constant rule we first differentiate x
0
to get 0x
−1
and then multiply by c.
Hence
if y = c then = c(0x
−1
) = 0
This result is also apparent from the graph of y = c, sketched in Figure 4.12, which is a
horizontal line c units away from the x axis. It is an important result and explains why lone
constants lurking in mathematical expressions disappear when differentiated.
Rule 2 The sum rule
If h(x) = f(x) + g(x) then h′(x) = f ′(x) + g′(x)
This rule tells you how to find the derivative of the sum of two functions:
differentiate each function separately and add
dy
dx
MFE_C04b.qxd 16/12/2005 11:11 Page 252
4.2 • Rules of differentiation
253
Figure 4.12
Example
Differentiate
(a) y = x
2
+ x
50
(b) y = x
3
+ 3
Solution
(a) To differentiate x
2
+ x
50
we need to differentiate x
2
and x
50
separately and to add. Now
x
2
differentiates to 2x
and
x
50
differentiates to 50x
49
so
if y = x
2
+ x
50
then = 2x + 50x
49
(b) To differentiate x
3
+ 3 we need to differentiate x
3
and 3 separately and to add. Now
x
3
differentiates to 3x
2
and
3 differentiates to 0
so
if y = x
3
+ 3 then = 3x
2
+ 0 = 3x
2
dy
dx
dy
dx
Practice Problem
2 Differentiate
(a)
y = x
5
+ x (b) y = x
2
+ 5
MFE_C04b.qxd 16/12/2005 11:11 Page 253

Differentiation
254
Practice Problem
3 Differentiate
(a)
y = x
2
− x
3
(b) y = 50 −
1
x
3
Example
Differentiate
(a) y = x
5
− x
2
(b) y = x −
Solution
(a) To differentiate x
5
− x
2
we need to differentiate x
5
and x
2
separately and to subtract. Now
x
5
differentiates to 5x
4
and
x
2
differentiates to 2x
so
if y = x
5
− x
2
then = 5x
4
− 2x
(b) To differentiate x − we need to differentiate x and separately and subtract. Now
x differentiates to 1
and
differentiates to −
so
if y = x − then = 1 −− =1 +
2
x
3
D
F
2
x
3
A
C
dy
dx
1
x
2
2
x
3
1
x
2
1
x
2
1
x
2
dy
dx
1
x
2
It is possible to combine these three rules and so to find the derivative of more involved
functions, as the following example demonstrates.
Rule 3 The difference rule
If h(x) = f(x) − g(x) then h′(x) = f ′(x) − g′(x)
This rule tells you how to find the derivative of the difference of two functions:
differentiate each function separately and subtract
MFE_C04b.qxd 16/12/2005 11:11 Page 254

4.2 • Rules of differentiation
255
Example
Differentiate
(a) y = 3x
5
+ 2x
3
(b) y = x
3
+ 7x
2
− 2x + 10 (c) y = 2 x +
Solution
(a) The sum rule shows that to differentiate 3x
5
+ 2x
3
we need to differentiate 3x
5
and 2x
3
separately and
to add. By the constant rule
3x
5
differentiates to 3(5x
4
) = 15x
4
and
2x
3
differentiates to 2(3x
2
) = 6x
2
so
if y = 3x
5
+ 2x
3
then = 15x
4
+ 6x
2
With practice you will soon find that you can just write the derivative down in a single line of work-
ing by differentiating term by term. For the function
y = 3x
5
+ 2x
3
we could just write
= 3(5x
4
) + 2(3x
2
) = 15x
4
+ 6x
2
(b) So far we have only considered expressions comprising at most two terms. However, the sum and dif-
ference rules still apply to lengthier expressions, so we can differentiate term by term as before. For the
function
y = x
3
+ 7x
2
− 2x + 10
we get
= 3x
2
+ 7(2x) − 2(1) + 0 = 3x
2
+ 14x − 2
(c) To differentiate
y = 2 x +
we first rewrite it using the notation of indices as
y = 2x
1/ 2
+ 3x
−1
Differentiating term by term then gives
= 2 x
−1/2
+ 3(−1)x
−2
= x
−1/2
− 3x
−2
which can be written in the more familiar form
=−
3
x
2
1
x
D
F
1
2
A
C
dy
dx
3
x
dy
dx
dy
dx
dy
dx
3
x
MFE_C04b.qxd 16/12/2005 11:11 Page 255

Whenever a function is differentiated, the thing that you end up with is itself a function. This
suggests the possibility of differentiating a second time to get the ‘slope of the slope function’.
This is written as
f ″(x)
or
For example, if
f(x) = 5x
2
− 7x + 12
then differentiating once gives
f ′(x) = 10x − 7
and if we now differentiate f ′(x) we get
f ″(x) = 10
The function f ′(x) is called the first-order derivative and f ″(x) is called the second-order
derivative.
d
2
y
dx
2
Differentiation
256
Practice Problem
4 Differentiate
(a)
y = 9x
5
+ 2x
2
(b) y = 5x
8
−
(c) y = x
2
+ 6x + 3 (d) y = 2x
4
+ 12x
3
− 4x
2
+ 7x − 400
3
x
Example
Evaluate f ″(1) where
f(x) = x
7
+
Solution
To find f ″(1) we need to differentiate
f(x) = x
7
+ x
−1
twice and to put x = 1 into the end result. Differentiating once gives
f ′(x) = 7x
6
+ (−1)x
−2
= 7x
6
− x
−2
and differentiating a second time gives
f ″(x) = 7(6x
5
) − (−2)x
−3
= 42x
5
+ 2x
−3
1
x
MFE_C04b.qxd 16/12/2005 11:11 Page 256

Finally, substituting x = 1 into
f ″(x) = 42x
5
+
gives
f ″(1) = 42 + 2 = 44
2
x
3
4.2 • Rules of differentiation
257
Practice Problem
5 Evaluate f″(6) where
f(x) = 4x
3
− 5x
2
It is possible to give a graphical interpretation of the sign of the second-order derivative.
Remember that the first-order derivative, f ′(x), measures the gradient of a curve. If the deriva-
tive of f ′(x) is positive (that is, if f ″(x) > 0) then f ′(x) is increasing. This means that the graph
gets steeper as you move from left to right and so the curve bends upwards. On the other hand,
if f ″(x) < 0, the gradient, f ′(x) must be decreasing, so the curve bends downwards. These
two cases are illustrated in Figure 4.13. For this function, f ″(x) < 0 to the left of x = a, and
f ″(x) > 0 to the right of x = a. At x = a itself, the curve changes from bending downwards to
bending upwards and at this point, f ″(a) = 0.
Figure 4.13
Example
Use the second-order derivative to show that the graph of the quadratic
y = ax
2
+ bx + c
bends upwards when a > 0 and bends downwards when a < 0.
MFE_C04b.qxd 16/12/2005 11:11 Page 257

Throughout this section the functions have all been of the form y = f(x), where the letters
x and y denote the variables involved. In economic functions, different symbols are used. It
should be obvious, however, that we can still differentiate such functions by applying the rules
of this section. For example, if a supply function is given by
Q = P
2
+ 3P + 1
and we need to find the derivative of Q with respect to P then we can apply the sum and dif-
ference rules to obtain
= 2P + 3
dQ
dP
Differentiation
258
Advice
Differentiation is a purely mechanical process that depends on the layout of the function
and not on the labels used to identify the variables. Problem 14 contains some additional
examples involving a variety of symbols. It is designed to boost your confidence before
you work through the applications described in the next section.
First-order derivative The rate of change of a function with respect to its independent
variable. It is the same as the ‘derivative’ of a function, y = f(x), and is written as f ′(x) or
dy/dx.
Second-order derivative The derivative of the first-order derivative. The expression
obtained when the original function, y = f(x), is differentiated twice in succession and is
written as f ″(x) or d
2
y/dx
2
.
Key Terms
Solution
If y = ax
2
+ bx + c then = 2ax + b and = 2a
If a > 0 then = 2a > 0 so the parabola bends upwards
If a < 0 then = 2a < 0 so the parabola bends downwards
Of course, if a = 0, the equation reduces to y = bx + c, which is the equation of a straight line, so the graph
bends neither upwards nor downwards.
d
2
y
dx
2
d
2
y
dx
2
d
2
y
dx
2
dy
dx
MFE_C04b.qxd 16/12/2005 11:11 Page 258

4.2 • Rules of differentiation
259
Practice Problems
6 Differentiate
(a)
y = 5x
2
(b) y = (c) y = 2x + 3
(d) y = x
2
+ x + 1 (e) y = x
2
− 3x + 2 (f) y = 3x −
(g) y = 2x
3
− 6x
2
+ 49x − 54 (h) y = ax + b (i) y = ax
2
+ bx + c
(j) y = 4 x −+
7 Evaluate f ′(x) for each of the following functions at the given point
(a)
f(x) = 3x
9
at x = 1
(b) f(x) = x
2
− 2x at x = 3
(c) f(x) = x
3
− 4x
2
+ 2x − 8 at x = 0
(d) f(x) = 5x
4
− at x =−1
(e) f(x) = x − at x = 4
8 By writing x
2
x
2
+ 2x −=x
4
+ 2x
3
− 5 differentiate x
2
x
2
+ 2x −
Use a similar approach to differentiate
(a)
x
2
(3x − 4) (b) x(3x
3
− 2x
2
+ 6x − 7) (c) (x + 1)(x − 6)
(d) (e) (f)
9 Find expressions for d
2
y/dx
2
in the case when
(a)
y = 7x
2
− x
(b) y =
(c) y = ax + b
10 Evaluate f ″(2) for the function
f(x) = x
3
− 4x
2
+ 10x − 7
11 Use the second-order derivative to show that the graph of the cubic,
f(x) = ax
3
+ bx
2
+ cx + d (a > 0)
bends upwards when x >−b/3a and bends downwards when x <−b/3a.
12 If f(x) = x
2
− 6x + 8, evaluate f′(3). What information does this provide about the graph of y = f(x) at
x = 3?
13 By writing 4x = 4 × x = 2 x, differentiate 4x.
Use a similar approach to differentiate
(a)
25x (b)
3
27x (c)
4
16x
3
(d)
25
x
1
x
2
x
2
− 3x + 5
x
2
x − 4x
2
x
3
x
2
− 3
x
D
F
5
x
2
A
C
D
F
5
x
2
A
C
2
x
4
x
4
7
x
2
3
x
7
x
3
x
MFE_C04b.qxd 16/12/2005 11:11 Page 259
