Jacques I. Mathematics for Economics and Business

Подождите немного. Документ загружается.

Notice that the values of MP

decline with increasing L. Part (a) shows that if the workforce consists of only

one person then to employ two people would increase output by approximately 146. In part (b) we see

that to increase the number of workers from 9 to 10 would result in about 46 additional units of output. In

part (c) we see that a 1 unit increase in labour from a level of 100 increases output by only 11. In part (d)

the situation is even worse. This indicates that to increase staff actually reduces output! The latter is a rather

surprising result, but it is borne out by what occurs in real production processes. This may be due to prob-

lems of overcrowding on the shopﬂoor or to the need to create an elaborate administration to organize the

larger workforce.

Differentiation

270

This example illustrates the law of diminishing marginal productivity (sometimes called the

law of diminishing returns). It states that the increase in output due to a 1 unit increase in

labour will eventually decline. In other words, once the size of the workforce has reached a cer-

tain threshold level, the marginal product of labour will get smaller. In the previous example,

the value of MP

continually goes down with rising L. This is not always so. It is possible for the

marginal product of labour to remain constant or to go up to begin with for small values of L.

However, if it is to satisfy the law of diminishing marginal productivity then there must be

some value of L above which MP

decreases.

A typical product curve is sketched in Figure 4.17, which has slope

= MP

Between 0 and L

the curve bends upwards, becoming progressively steeper, and so the slope

function, MP

, increases. Mathematically, this means that the slope of MP

is positive: that is,

> 0

Now MP

is itself the derivative of Q with respect to L, so we can use the notation for the sec-

ond derivative and write this as

> 0

d(MP

)

MFE_C04c.qxd 16/12/2005 11:12 Page 270

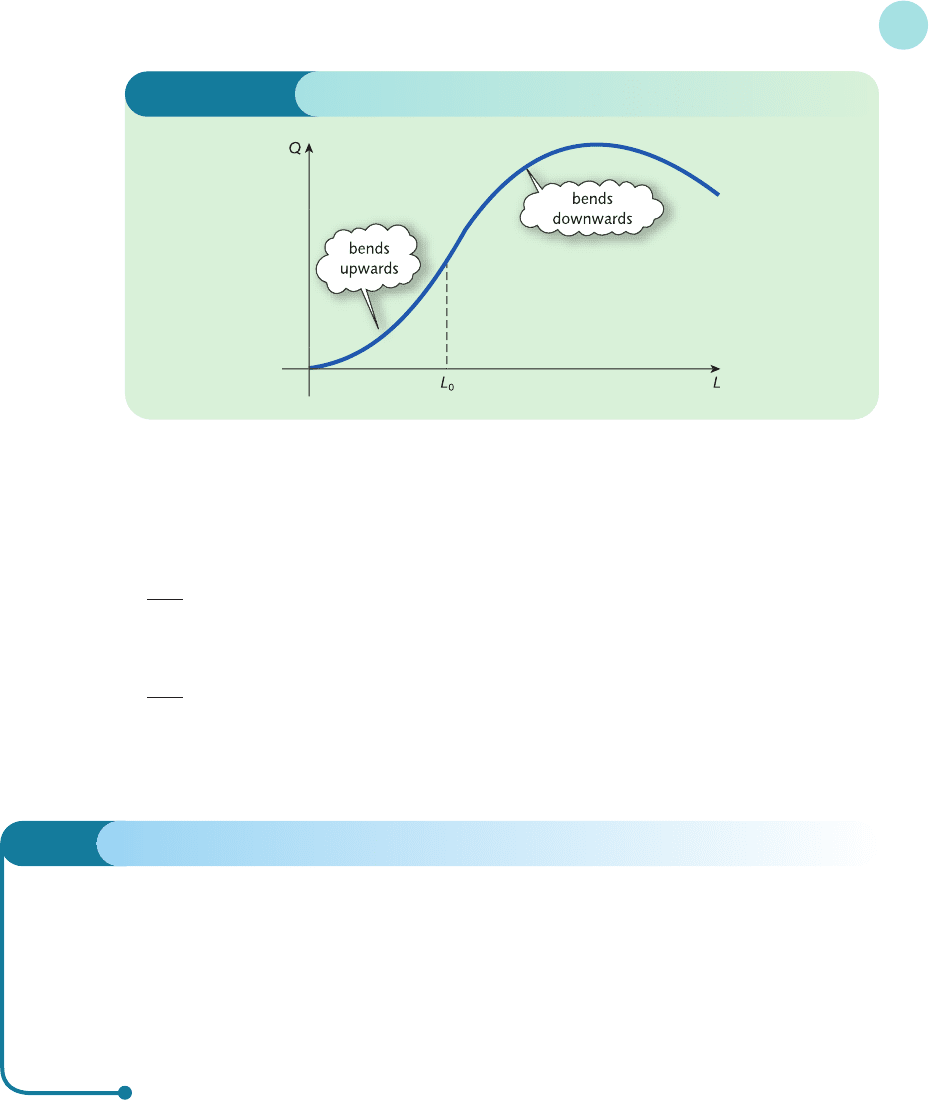
Similarly, if L exceeds the threshold value of L

, then Figure 4.17 shows that the product curve

bends downwards and the slope decreases. In this region, the slope of the slope function is neg-

ative, so that

< 0

The law of diminishing returns states that this must happen eventually: that is,

< 0

for sufﬁciently large L.

4.3 • Marginal functions

271

Figure 4.17

Practice Problem

4 A Cobb–Douglas production function is given by

Q = 5L

1/ 2

Assuming that capital, K, is fixed at 100, write down a formula for Q in terms of L only. Calculate the

marginal product of labour when

(a)

L = 1 (b) L = 9 (c) L = 10 000

Verify that the law of diminishing marginal productivity holds in this case.

4.3.3 Consumption and savings

In Chapter 1 the relationship between consumption, C, savings, S, and national income, Y, was

investigated. If we assume that national income is only used up in consumption and savings

then

Y = C + S

MFE_C04c.qxd 16/12/2005 11:12 Page 271

Differentiation

272

Example

If the consumption function is

C = 0.01Y

+ 0.2Y + 50

calculate MPC and MPS when Y = 30.

Solution

In this example the consumption function is given, so we begin by ﬁnding MPC. To do this we differenti-

ate C with respect to Y. If

Of particular interest is the effect on C and S due to variations in Y. Expressed simply, if national

income rises by a certain amount, are people more likely to go out and spend their extra income

on consumer goods or will they save it? To analyse this behaviour we use the concepts marginal

propensity to consume, MPC, and marginal propensity to save, MPS, which are deﬁned by

MPC = and MPS =

marginal propensity to consume is the derivative of

consumption with respect to income

marginal propensity to save is the derivative of savings with respect to income

These deﬁnitions are consistent with those given in Section 1.6, where MPC and MPS were

taken to be the slopes of the linear consumption and savings curves, respectively. At ﬁrst sight

it appears that, in general, we need to work out two derivatives in order to evaluate MPC

and MPS. However, this is not strictly necessary. Recall that we can do whatever we like to

an equation provided we do the same thing to both sides. Consequently, we can differentiate

both sides of the equation

Y = C + S

with respect to Y to deduce that

=+=MPC + MPS

Now we are already familiar with the result that when we differentiate x with respect to x the

answer is 1. In this case Y plays the role of x, so

= 1

Hence

1 = MPC + MPS

This formula is identical to the result given in Section 1.6 for simple linear functions. In

practice, it means that we need only work out one of the derivatives. The remaining derivative

can then be calculated directly from this equation.

MFE_C04c.qxd 16/12/2005 11:12 Page 272

C = 0.01Y

+ 0.2Y + 50

then

= 0.02Y + 0.2

so, when Y = 30,

MPC = 0.02(30) + 0.2 = 0.8

To ﬁnd the corresponding value of MPS we use the formula

MPC + MPS = 1

which gives

MPS = 1 − MPC = 1 − 0.8 = 0.2

This indicates that when national income increases by 1 unit (from its current level of 30) consumption

rises by approximately 0.8 units, whereas savings rise by only about 0.2 units. At this level of income the

nation has a greater propensity to consume than it has to save.

4.3 • Marginal functions

273

Practice Problem

5 If the savings function is given by

S = 0.02Y

− Y + 100

calculate the values of MPS and MPC when Y = 40. Give a brief interpretation of these results.

Average revenue Total revenue per unit of output: AR = TR/Q = P.

Law of diminishing marginal productivity or law of diminishing returns Once the size of

the workforce exceeds a particular value, the increase in output due to a 1 unit increase in

labour will decline: d

Q/dL

< 0 for sufﬁciently large L.

Marginal cost The cost of producing 1 more unit of output: MC = d(TC)/dQ.

Marginal product of labour The extra output produced by 1 more unit of labour:

= dQ/dL.

Marginal propensity to consume The fraction of a rise in national income which goes on

consumption: MPC = dC/dY.

Marginal propensity to save The fraction of a rise in national income which goes into

savings: MPS = dS/dY.

Marginal revenue The extra revenue gained by selling 1 more unit of a good:

MR = d(TR)/dQ.

Monopolist The only ﬁrm in the industry.

Perfect competition A situation in which there are no barriers to entry in an industry

where there are many ﬁrms selling an identical product at the market price.

Key Terms

MFE_C04c.qxd 16/12/2005 11:12 Page 273

Differentiation

274

Practice Problems

6 If the demand function is

P = 100 − 4Q

find expressions for TR and MR in terms of Q. Hence estimate the change in TR brought about by a

0.3 unit increase in output from a current level of 12 units.

7 If the demand function is

P = 80 − 3Q

show that

MR = 2P − 80

8 A monopolist’s demand function is given by

P + Q = 100

Write down expressions for TR and MR in terms of Q and sketch their graphs. Find the value of Q

which gives a marginal revenue of zero and comment on the significance of this value.

9 The fixed costs of producing a good are 100 and the variable costs are 2 + Q/10 per unit.

(a) Find expressions for TC and MC.

(b) Evaluate MC at Q = 30 and hence estimate the change in TC brought about by a 2 unit increase

in output from a current level of 30 units.

10 If the average cost function of a good is

AC =+2Q + 9

find an expression for TC. What are the fixed costs in this case? Write down an expression for the

marginal cost function.

11 A firm’s production function is

Q = 50L − 0.01L

where L denotes the size of the workforce. Find the value of MP

in the case when

(a)

L = 1 (b) L = 10 (c) L = 100 (d) L = 1000

Does the law of diminishing marginal productivity apply to this particular function?

12 Show that the law of diminishing marginal productivity holds for the production function

Q = 6L

− 0.2L

13 If the consumption function is

C = 50 + 2 Y

calculate MPC and MPS when Y = 36 and give an interpretation of these results.

14 The consumption function is

C = 0.01Y

+ 0.8Y + 100

(a) Calculate the values of MPC and MPS when Y = 8.

(b) Use the fact that C + S = Y to obtain a formula for S in terms of Y. By differentiating this expres-

sion find the value of MPS at Y = 8 and verify that this agrees with your answer to part (a).

MFE_C04c.qxd 16/12/2005 11:12 Page 274

section 4.4

Further rules of

differentiation

Section 4.2 introduced you to the basic rules of differentiation. Unfortunately, not all functions

can be differentiated using these rules alone. For example, we are unable to differentiate the

functions

x√(2x − 3) and

using just the constant, sum or difference rules. The aim of the present section is to describe

three further rules which allow you to ﬁnd the derivative of more complicated expressions.

Indeed, the totality of all six rules will enable you to differentiate any mathematical function.

Although you may ﬁnd that the rules described in this section take you slightly longer to grasp

than before, they are vital to any understanding of economic theory.

The ﬁrst rule that we investigate is called the chain rule and it can be used to differentiate

functions such as

y = (2x + 3)

and y =√(1 + x

)

The distinguishing feature of these expressions is that they represent a ‘function of a function’.

To understand what we mean by this, consider how you might evaluate

y = (2x + 3)

+ 1

Objectives

At the end of this section you should be able to:

 Use the chain rule to differentiate a function of a function.

 Use the product rule to differentiate the product of two functions.

 Use the quotient rule to differentiate the quotient of two functions.

 Differentiate complicated functions using a combination of rules.

MFE_C04d.qxd 16/12/2005 11:13 Page 275

Differentiation

276

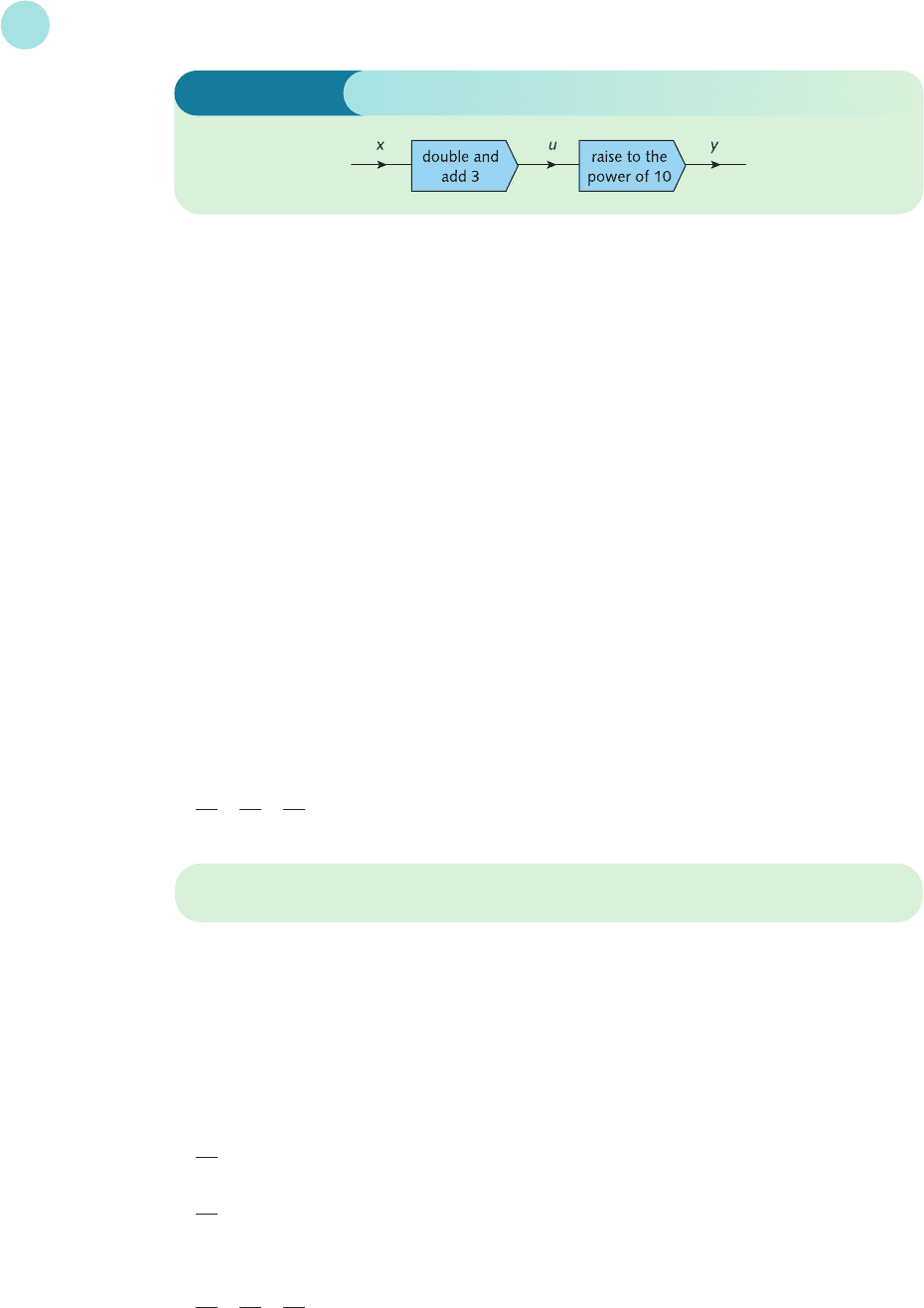
Figure 4.18

on a calculator. You would ﬁrst work out an intermediate number u, say, given by

u = 2x + 3

and then raise it to the power of 10 to get

y = u

This process is illustrated using the ﬂow chart in Figure 4.18. Note how the incoming number

x is ﬁrst processed by the inner function, ‘double and add 3’. The output u from this is

then passed on to the outer function, ‘raise to the power of 10’, to produce the ﬁnal outgoing

number y.

The function

y =√(1 + x

)

can be viewed in the same way. To calculate y you perform the inner function, ‘square and add

1’, followed by the outer function, ‘take square roots’.

The chain rule for differentiating a function of a function may now be stated.

Rule 4 The chain rule

If y is a function of u, which is itself a function of x, then

=×

differentiate the outer function and multiply by the derivative of the inner function

To illustrate this rule, let us return to the function

y = (2x + 3)

in which

y = u

and u = 2x + 3

Now

= 10u

= 10(2x + 3)

= 2

The chain rule then gives

=×=10(2x + 3)

(2) = 20(2x + 3)

MFE_C04d.qxd 16/12/2005 11:13 Page 276

With practice it is possible to perform the differentiation without explicitly introducing the

variable u. To differentiate

y = (2x + 3)

we ﬁrst differentiate the outer power function to get

10(2x + 3)

and then multiply by the derivative of the inner function, 2x + 3, which is 2, so

= 20(2x + 3)

4.4 • Further rules of differentiation

277

Example

Differentiate

(a) y = (3x

− 5x + 2)

(b) y =

)

Solution

(a) The chain rule shows that to differentiate (3x

− 5x + 2)

we ﬁrst differentiate the outer power function

to get

4(3x

− 5x + 2)

and then multiply by the derivative of the inner function, 3x

− 5x + 2, which is 6x − 5. Hence if

y = (3x

− 5x + 2)

then = 4(3x

− 5x + 2)

(6x − 5)

(b) To use the chain rule to differentiate

y =

recall that reciprocals are denoted by negative powers, so that

y = (3x + 7)

−1

The outer power function differentiates to get

−(3x + 7)

−2

and the inner function, 3x + 7, differentiates to get 3. By the chain rule we just multiply these together

to deduce that

if y = then =−(3x + 7)

−2

(3) =

y =√(1 + x

)

recall that roots are denoted by fractional powers, so that

y = (1 + x

)

1/ 2

−3

(3x + 7)

3x + 7



MFE_C04d.qxd 16/12/2005 11:13 Page 277

The outer power function differentiates to get

(1 + x

)

−1/ 2

and the inner function, 1 + x

, differentiates to get 2x. By the chain rule we just multiply these together

to deduce that

if y =√(1 + x

) then = (1 + x

)

−1/ 2

(2x) =

(1 + x

)

Differentiation

278

Example

Differentiate

(a) y = x

(2x + 1)

(b) x√(6x + 1) (c) y =

Solution

(a) The function x

(2x + 1)

involves the product of two simpler functions, namely x

and (2x + 1)

, which we

denote by u and v respectively. (It does not matter which function we label u and which we label v. The

same answer is obtained if u is (2x + 1)

and v is x

. You might like to check this for yourself later.) Now if

u = x

and v = (2x + 1)

then

= 2x and = 6(2x + 1)

1 + x

Practice Problem

1 Differentiate

(a)

y = (3x − 4)

(b) y = (x

+ 3x + 5)

2x − 3

The next rule is used to differentiate the product of two functions, f(x)g(x). In order to give

a clear statement of this rule, we write

u = f(x) and v = g(x)

Rule 5 The product rule

If y = uv then = u × v

This rule tells you how to differentiate the product of two functions:

multiply each function by the derivative of the other and add

MFE_C04d.qxd 16/12/2005 11:13 Page 278

where we have used the chain rule to ﬁnd dv/dx. By the product rule,

= u + v

= x

[6(2x + 1)

] + (2x + 1)

(2x)

The ﬁrst term is obtained by leaving u alone and multiplying it by the derivative of v. Similarly, the

second term is obtained by leaving v alone and multiplying it by the derivative of u.

If desired, the ﬁnal answer may be simpliﬁed by taking out a common factor of 2x(2x + 1)

. This

factor goes into the ﬁrst term 3x times and into the second 2x + 1 times. Hence

= 2x (2x + 1)

[3x + (2x + 1)]

= 2x(2x + 1)

(5x + 1)

(b) The function x√(6x + 1) involves the product of the simpler functions

u = x and v =√(6x + 1) = (6x + 1)

1/ 2

for which

= 1 and = (6x + 1)

−1/ 2

× 6 = 3(6x + 1)

−1/ 2

where we have used the chain rule to ﬁnd dv/dx. By the product rule,

= u + v

= x[3(6x + 1)

−1/ 2

] + (6x + 1)

1/ 2

(1)

=+√(6x + 1)

If desired, this can be simpliﬁed by putting the second term over a common denominator

√(6x + 1)

To do this we multiply the top and bottom of the second term by √(6x + 1) to get

Hence

since it appears to be the quotient and not the product of two functions. However, if we recall that

reciprocals are equivalent to negative powers, we may rewrite it as

x(1 + x)

−1

It follows that we can put

u = x and v = (1 + x)

−1

1 + x

9x + 1

(6x + 1)

3x + (6x + 1)

(6x + 1)

6x + 1

(6x + 1)

4.4 • Further rules of differentiation

279



MFE_C04d.qxd 16/12/2005 11:13 Page 279