Jacques I. Mathematics for Economics and Business

Подождите немного. Документ загружается.

To ﬁnd the value of E we also need to calculate

from the demand equation, P =−Q

− 4Q + 96. It is not at all easy to transpose this for Q. Indeed, we would

have to use the formula for solving a quadratic, as above, replacing the number 51 by the letter P.

Unfortunately this expression involves square roots and the subsequent differentiation is quite messy. (You

might like to have a go at this yourself !) However, it is easy to differentiate the given expression with respect

to Q to get

=−2Q − 4

and so

Finally, putting Q = 5 gives

=−

The price elasticity of demand is given by

E =− ×

and if we substitute P = 51, Q = 5 and dQ/dP =−1/14 we get

E =− ×− = 0.73

To discover the effect on Q due to a 2% rise in P we return to the original deﬁnition

E =−

We know that E = 0.73 and that the percentage change in price is 2, so

0.73 =−

which shows that demand changes by

−0.73 × 2 =−1.46%

A 2% rise in price therefore leads to a fall in demand of 1.46%.

percentage change in demand

percentage change in price

−2Q − 4

dP/dQ

Differentiation

290

Practice Problem

3 Given the demand equation

P =−Q

− 10Q + 150

find the price elasticity of demand when Q = 4. Estimate the percentage change in price needed to

increase demand by 10%.

MFE_C04e.qxd 16/12/2005 11:15 Page 290

The price elasticity of supply is deﬁned in an analogous way to that of demand. We deﬁne

E =

This time, however, there is no need to ﬁddle the sign. An increase in price leads to an increase

in supply, so E is automatically positive. In symbols,

E = ×

If (Q

, P

) and (Q

, P

) denote two points on the supply curve then arc elasticity is obtained, as

before, by setting

∆P = P

− P

∆Q = Q

− Q

P =

/2(P

+ P

)

Q =

2(Q

+ Q

)

The corresponding formula for point elasticity is

E = ×

∆Q

∆P

percentage change in supply

percentage change in price

4.5 • Elasticity

291

Example

Given the supply function

P = 10 + Q

ﬁnd the price elasticity of supply

(a) averaged along an arc between Q = 100 and Q = 105

(b) at the point Q = 100

Solution

(a) We are given that

= 100, Q

= 105

so that

= 10 + 100 = 20 and P

= 10 + 105 = 20.247

Hence

∆P = 20.247 − 20 = 0.247, ∆Q = 105 − 100 = 5

P = (20 + 20.247) = 20.123, Q = (100 + 105) = 102.5

The formula for arc elasticity gives

E = × = × = 3.97

0.247

20.123

102.5

∆Q

∆P



MFE_C04e.qxd 16/12/2005 11:15 Page 291

(b) To evaluate the elasticity at the point Q = 100, we need to ﬁnd the derivative, . The supply equation

P = 10 + Q

1/ 2

differentiates to give

= Q

−1/ 2

so that

= 2 Q

At the point Q = 100, we get

= 2 100 = 20

The formula for point elasticity gives

E = × = × 20 = 4

Notice that, as expected, the answers to parts (a) and (b) are nearly the same.

100

Differentiation

292

Advice

The concept of elasticity can be applied to more general functions and we consider some

of these in the next chapter. For the moment we investigate the theoretical properties of

demand elasticity. The following material is more difficult to understand than the fore-

going, so you may prefer just to concentrate on the conclusions and skip the intermediate

derivations.

Practice Problem

4 If the supply equation is

Q = 150 + 5P + 0.1P

calculate the price elasticity of supply

(a) averaged along an arc between P = 9 and P = 11

(b) at the point P = 10

We begin by analysing the relationship between elasticity and marginal revenue. Marginal

revenue, MR, is given by

MR =

d(TR)

MFE_C04e.qxd 16/12/2005 11:15 Page 292

Now TR is equal to the product PQ, so we can apply the product rule to differentiate it. If

u = P and v = Q

then

= and ==1

By the product rule

MR = u + v

= P + Q ×

= P 1 +×

Now

− × = E

× =−

This can be substituted into the expression for MR to get

MR = P 1 −

The connection between marginal revenue and demand elasticity is now complete, and this

formula can be used to justify the intuitive argument that we gave at the beginning of this

section concerning revenue and elasticity. Observe that if E < 1 then 1/E > 1, so MR is negative

for any value of P. It follows that the revenue function is decreasing in regions where demand

is inelastic, because MR determines the slope of the revenue curve. Similarly, if E > 1 then

1/E < 1, so MR is positive for any price, P, and the revenue curve is uphill. In other words,

the revenue function is increasing in regions where demand is elastic. Finally, if E = 1 then

MR is 0, and so the slope of the revenue curve is horizontal at points where demand is unit

elastic.

Throughout this section we have taken speciﬁc functions and evaluated the elasticity at

particular points. It is more instructive to consider general functions and to deduce general

expressions for elasticity. Consider the standard linear downward-sloping demand function

P = aQ + b

when a < 0 and b > 0. As noted in Section 4.3, this typiﬁes the demand function faced by a

monopolist. To transpose this equation for Q, we subtract b from both sides to get

aQ = P − b

and then divide through by a to get

Q = (P − b)

4.5 • Elasticity

293

MFE_C04e.qxd 16/12/2005 11:15 Page 293

Hence

The formula for elasticity of demand is

E =−

so replacing Q by (1/a)(P − b) and dQ/dP by 1/a gives

E =×

Notice that this formula involves P and b but not a. Elasticity is therefore independent of the

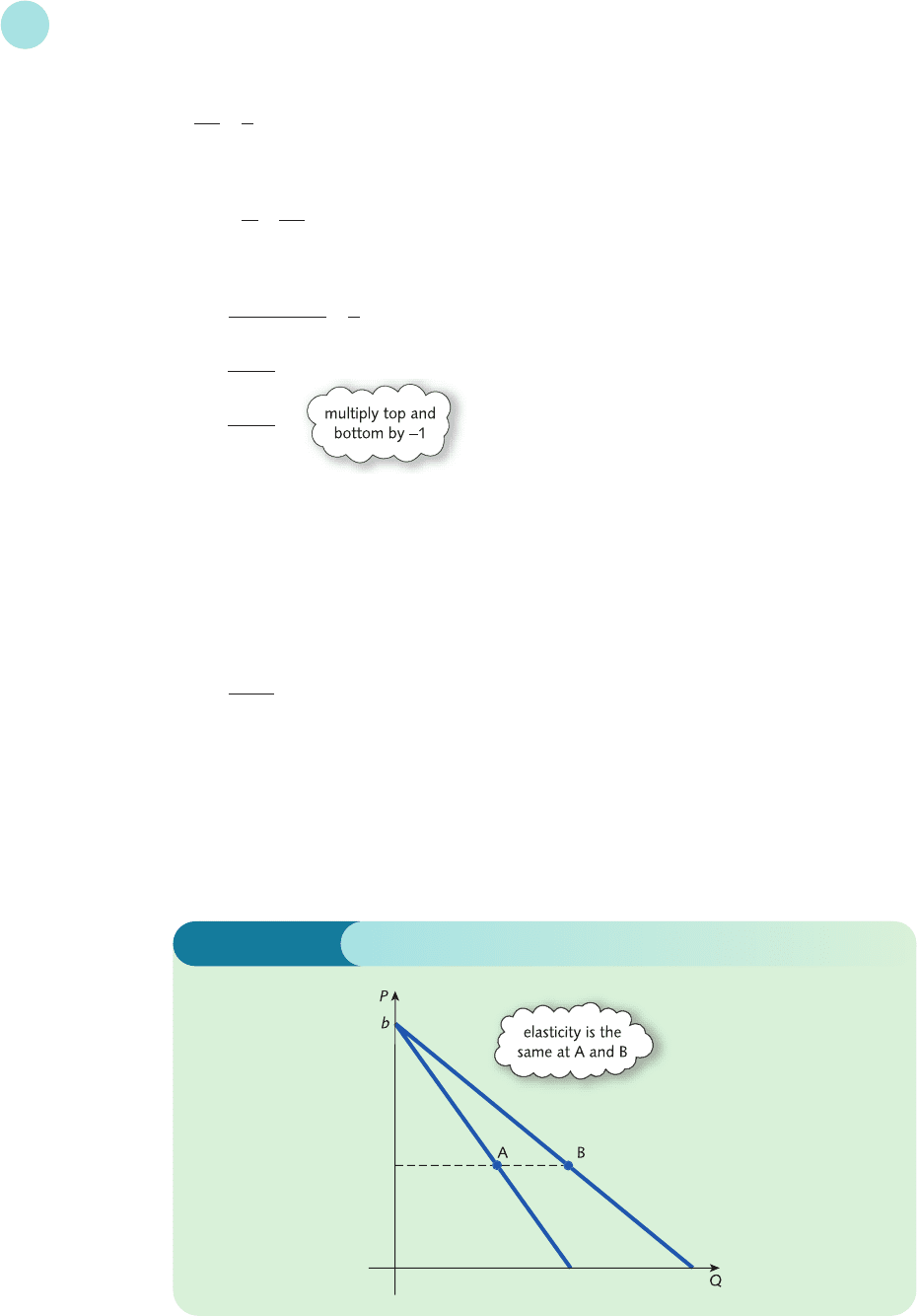
slope of linear demand curves. In particular, this shows that, corresponding to any price P, the

elasticities of the two demand functions sketched in Figure 4.20 are identical. This is perhaps a

rather surprising result. We might have expected demand to be more elastic at point A than at

point B, since A is on the steeper curve. However, the mathematics shows that this is not the

case. (Can you explain, in economic terms, why this is so?)

Another interesting feature of the result

E =

is the fact that b occurs in the denominator of this fraction, so that corresponding to any price,

P, the larger the value of the intercept, b, the smaller the elasticity. In Figure 4.21, elasticity at

C is smaller than that at D because C lies on the curve with the larger intercept.

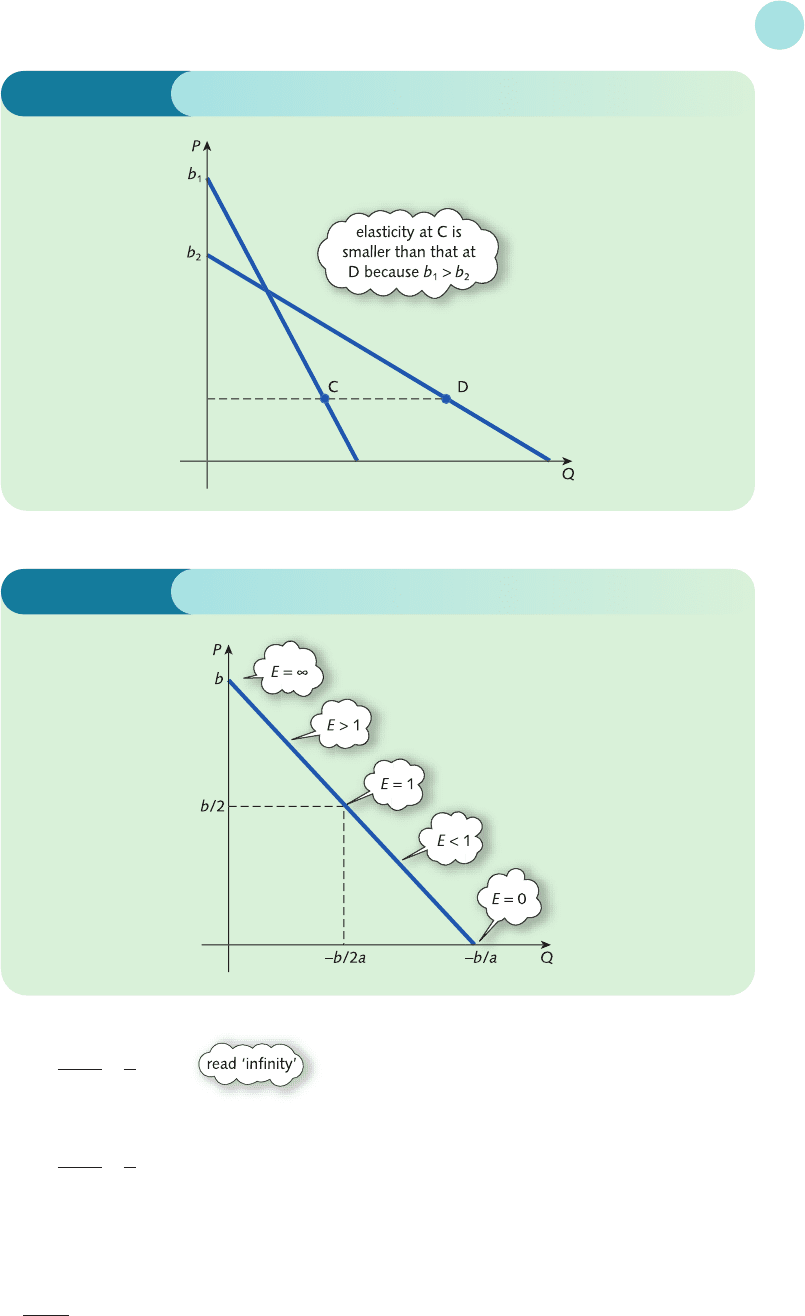
The dependence of E on P is also worthy of note. It shows that elasticity varies along a

linear demand curve. This is illustrated in Figure 4.22. At the left-hand end, P = b, so

b − P

−P

P − b

−P

(1/a)(P − b)

Differentiation

294

Figure 4.20

MFE_C04e.qxd 16/12/2005 11:15 Page 294

E ===∞

At the right-hand end, P = 0, so

E ===0

As you move down the demand curve, the elasticity decreases from ∞ to 0, taking all pos-

sible values. Demand is unit elastic when E = 1 and the price at which this occurs can be found

by solving

= 1 for P

b − P

b − 0

b − b

4.5 • Elasticity

295

Figure 4.21

Figure 4.22

MFE_C04e.qxd 16/12/2005 11:15 Page 295

P = b − P (multiply both sides by b − P)

2P = b (add P to both sides)

P = (divide both sides by 2)

The corresponding quantity can be found by substituting P = b/2 into the transposed demand

equation to get

Q = − b =−

Demand is unit elastic exactly halfway along the demand curve. To the left of this point E > 1

and demand is elastic, whereas to the right E < 1 and demand is inelastic.

In our discussion of general demand functions, we have concentrated on those which are

represented by straight lines since these are commonly used in simple economic models. There

are other possibilities and Practice Problem 11 investigates a class of functions that have con-

stant elasticity.

Differentiation

296

Practice Problems

5 Given the demand function

P = 500 − 4Q

calculate the price elasticity of demand averaged along an arc joining Q = 8 and Q = 10.

6 Find the price elasticity of demand at the point Q = 9 for the demand function

P = 500 − 4Q

and compare your answer with that of Practice Problem 5.

7 Find the price elasticity of demand at P = 6 for each of the following demand functions:

(a)

P = 30 − 2Q

(b) P = 30 − 12Q

Arc elasticity Elasticity measured between two points on a curve.

Elastic demand Where the percentage change in demand is more than the corresponding

percentage change in price: E > 1.

Inelastic demand Where the percentage change in demand is less than the corresponding

percentage change in price: E < 1.

Price elasticity of demand A measure of the responsiveness of the change in demand due

to a change in price: − (percentage change in demand) ÷ (percentage change in price).

Price elasticity of supply A measure of the responsiveness of the change in supply due to

a change in price: (percentage change in supply) ÷ (percentage change in price).

Unit elastic demand Where the percentage change in demand is the same as the percent-

age change in price: E = 1.

Key Terms

MFE_C04e.qxd 16/12/2005 11:15 Page 296

8 If the demand equation is

Q + 4P = 60

find a general expression for the price elasticity of demand in terms of P. For what value of P is

demand unit elastic?

9 Consider the supply equation

Q = 4 + 0.1P

(a) Write down an expression for dQ/dP.

(b) Show that the supply equation can be rearranged as

P =√(10Q − 40)

Differentiate this to find an expression for dP/dQ.

(d) Calculate the elasticity of supply at the point Q

14.

10 If the supply equation is

Q = 7 + 0.1P + 0.004P

find the price elasticity of supply if the current price is 80.

(a) Is supply elastic, inelastic or unit elastic at this price?

(b) Estimate the percentage change in supply if the price rises by 5%.

11 Show that the price elasticity of demand is constant for the demand functions

P =

where A and n are positive constants.

12 Find a general expression for the point elasticity of supply for the function,

Q = aP + b (a > 0)

Deduce that the supply function is

(a) unit elastic when b = 0

(b) inelastic when b > 0

Give a brief geometrical interpretation of these results.

dP/dQ

4.5 • Elasticity

297

MFE_C04e.qxd 16/12/2005 11:15 Page 297

section 4.6

Optimization of

economic functions

In Section 2.1 a simple three-step strategy was described for sketching graphs of quadratic func-

tions of the form

f(x) = ax

+ bx + c

The basic idea is to solve the corresponding equation

+ bx + c = 0

to ﬁnd where the graph crosses the x axis. Provided that the quadratic equation has at least one

solution, it is then possible to deduce the coordinates of the maximum or minimum point of

the parabola. For example, if there are two solutions, then by symmetry the graph turns round

at the point exactly halfway between these solutions. Unfortunately, if the quadratic equation

has no solution then only a limited sketch can be obtained using this approach.

In this section we show how the techniques of calculus can be used to ﬁnd the coordinates

of the turning point of a parabola. The beauty of this approach is that it can be used to locate

the maximum and minimum points of any economic function, not just those represented by

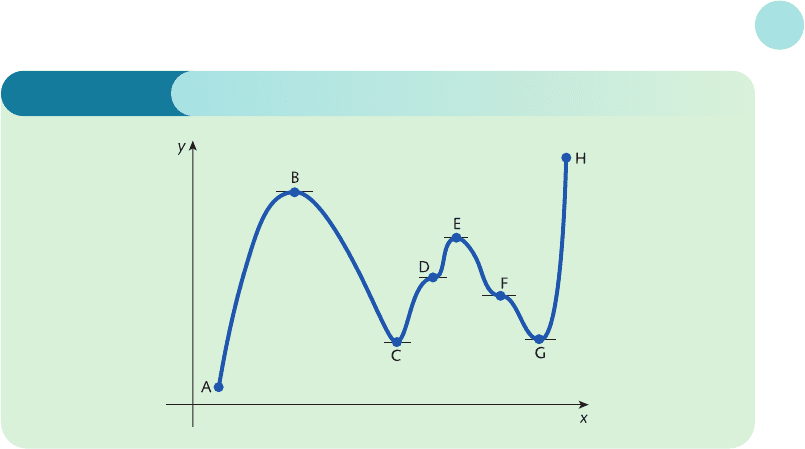
quadratics. Look at the graph in Figure 4.23 (overleaf). Points B, C, D, E, F and G are referred

to as the stationary points (sometimes called critical points, turning points or extrema) of the

function. At a stationary point the tangent to the graph is horizontal and so has zero slope.

Objectives

At the end of this section you should be able to:

 Use the ﬁrst-order derivative to ﬁnd the stationary points of a function.

 Use the second-order derivative to classify the stationary points of a function.

 Find the maximum and minimum points of an economic function.

 Use stationary points to sketch graphs of economic functions.

MFE_C04f.qxd 16/12/2005 11:16 Page 298

Consequently, at a stationary point of a function f(x),

f ′(x) = 0

The reason for using the word ‘stationary’ is historical. Calculus was originally used by

astronomers to predict planetary motion. If a graph of the distance travelled by an object is

sketched against time then the speed of the object is given by the slope, since this represents the

rate of change of distance with respect to time. It follows that if the graph is horizontal at some

point then the speed is zero and the object is instantaneously at rest: that is, stationary.

Stationary points are classiﬁed into one of three types: local maxima, local minima and

stationary points of inﬂection.

At a local maximum (sometimes called a relative maximum) the graph falls away on both

sides. Points B and E are the local maxima for the function sketched in Figure 4.23. The word

‘local’ is used to highlight the fact that, although these are the maximum points relative to their

locality or neighbourhood, they may not be the overall or global maximum. In Figure 4.23 the

highest point on the graph actually occurs at the right-hand end, H, which is not a stationary

point, since the slope is not zero at H.

At a local minimum (sometimes called a relative minimum) the graph rises on both sides.

Points C and G are the local minima in Figure 4.23. Again, it is not necessary for the global

minimum to be one of the local minima. In Figure 4.23 the lowest point on the graph occurs

at the left-hand end, A, which is not a stationary point.

At a stationary point of inﬂection the graph rises on one side and falls on the other. The sta-

tionary points of inﬂection in Figure 4.23 are labelled D and F. These points are of little value

in economics, although they do sometimes assist in sketching graphs of economic functions.

Maxima and minima, on the other hand, are important. The calculation of the maximum

points of the revenue and proﬁt functions is clearly worthwhile. Likewise, it is useful to be able

to ﬁnd the minimum points of average cost functions.

For most examples in economics, the local maximum and minimum points coincide

with the global maximum and minimum. For this reason we shall drop the word ‘local’ when

describing stationary points. However, it should always be borne in mind that the global

maximum and minimum could actually be attained at an end point and this possibility may

need to be checked. This can be done by comparing the function values at the end points

with those of the stationary points and then deciding which of them gives rise to the largest or

smallest values.

4.6 • Optimization of economic functions

299

Figure 4.23

MFE_C04f.qxd 16/12/2005 11:16 Page 299