Иванов-Смоленский А.В. Электрические машины т 2

Подождите немного. Документ загружается.

430

статора и ротора по осям d, q (u

, u

), равноценную системе

(69.32), (69.38):

(69.39)

Составляющие потокосцеплений в этих уравнениях выражаются

через соответствующие составляющие токов

(69.40)

Рассмотрим уравнение напряжений ротора по продольной оси

(69.39) совместно с уравнением для потокосцепления статора по про-

дольной оси (69.40). Продифференцировав последнее уравнение и

считая ротор короткозамкнутым, получим следующую систему:

;

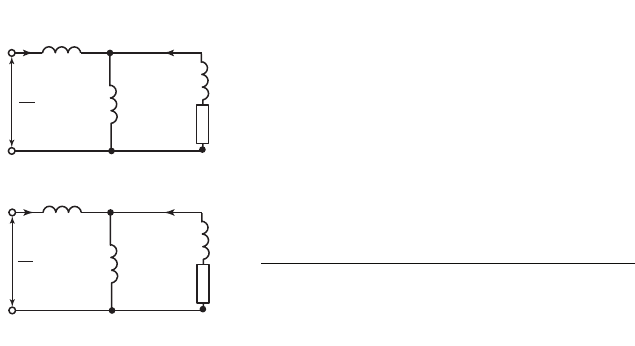
которой соответствует электрическая эквивалентная схема замеще-

ния по продольной оси, показанная на рис. 69.5, а. Поступая таким же

образом с уравнениями напряжения и потокосцепления по попереч-

ной оси, получаем электрическую схему замещения по поперечной

оси, показанную на рис. 69.5, б. Эти схе-

мы отражают магнитные трансформа-

торные связи между эквивалентными об-

мотками статора и ротора, расположен-

ными по продольной или поперечной

оси машины. С их помощью удобно про-

водить анализ переходных процессов в

асинхронных машинах.

Сравнивая уравнение напряжений ста-

тора, записанное в неподвижных осях α, β

(69.31), с тем же уравнением, записанным

dΨ

--------------

ωΨ

–+= ; u

dΨ

--------------

ωΨ

++= ;

dΨ

--------------

+= ; u

dΨ

--------------

+= .

⎭

⎪

⎬

⎪

⎫

12m

;+=

12m

;+=

12m

;+=

12m

.+=

⎭

⎬

⎫

-----

12m

+()=

0 R

-----

12m

+()+=

;

а)

б)

Рис. 69.5. Эквивалентные схемы замещения

асинхронной машины по продольной (а) и по-

перечной (б) осям

431

во вращающихся со скоростью ω осях ротора d, q (69.38), можно заме-

тить, что в последнем содержится дополнительно ЭДС вращения

( ), пропорциональная угловой скорости осей, в которых записано

уравнение относительно рассматриваемой обмотки. К тому же выводу

приводит сопоставление уравнения напряжений ротора, записанного в

собственных осях d, q (69.32), с тем же уравнением в неподвижных

осях α, β (69.34). В последнем появляется дополнительная ЭДС враще-

ния ( ), пропорциональная угловой скорости неподвижных осей

α, β относительно вращающегося ротора, которая равна –ω. В общем

случае, когда требуется записать уравнение в осях, вращающихся с

произвольной скоростью ω

, в уравнение напряжений войдет дополни-

тельная ЭДС вращения, пропорциональная угловой скорости этих осей

относительно рассматриваемой обмотки. Поэтому уравнение напряже-

ний статора в осях, вращающихся со скоростью ω

, содержит ЭДС, про-

порциональную угловой скорости этих осей относительно неподвиж-

ной обмотки статора, которая равна ω

. (69.41)

Соответственно уравнение напряжений ротора в осях, вращаю-

щихся со скоростью ω

, содержит ЭДС, пропорциональную угловой

скорости этих осей относительно вращающегося со скоростью ω ро-

тора, которая равна ω

– ω:

. (69.42)

Само собой разумеется, все величины, входящие в (69.41), (69.42),

должны быть выражены в рассматриваемой комплексной плоскости,

вращающейся со скоростью ω

. Если принять, что при t = 0 действи-

тельная ось этой комплексной плоскости совпадает с осью фазы А

статора, а в момент t смещена относительно оси фазы А на угол α

, то

токи в (69.41), (69.42) равны:

; , (69.43)

где — комплексная функция тока статора в собственной ком-

плексной плоскости α, β; — комплексная функция тока ротора

в собственной комплексной плоскости d, q.

ωΨ

∼

– jωΨ

∼

d Ψ

∼

----------

jω

∼

++=

∼

d Ψ

∼

----------

j ω

ω–()Ψ

∼

++=

∼

1 αβ()

– jα

= I

∼

2 dq()

– j α

α–()

∼

1 αβ()

∼

2 dq()

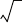
432

Потокосцепления в (69.41), (69.42) выражаются через токи и :

; . (69.43а)

69.9. Выражение элетроманитноо момента

через резльтирющие омплесные фнции тоов

и потоосцеплений и их составляющие

Выведенная выше довольно громоздкая формула для электромаг-

нитного момента (69.21), в которую входят произведения фазных то-

ков статора и ротора (i

и i

) и синусы изменяющихся углов между

соответствующими фазами α

, может быть заметно упрощена с по-

мощью результирующих комплексных функций токов. Докажем, что

электромагнитный момент выражается в общем случае через резуль-

тирующие комплексные функции точно так же, как средний электро-

магнитный момент в установившемся симметричном режиме — через

комплексы величин прямой последовательности (§ 29.1).

Учитывая, что результирующие комплексные функции токов в

раз больше, чем комплексы действующих значений токов, через кото-

рые выражены средние моменты в § 29.1, можно рассчитать электро-

магнитный момент, приложенный к ротору, по формуле

(69.44)

и равный ему электромагнитный момент, приложенный к статору, по

формуле

. (69.45)

Заметим, что момент, действующий на ротор, считается положи-

тельным, если он направлен в сторону вращения (т.е. против часовой

стрелки); момент, действующий на статор, считается положитель-

ным, если он направлен против вращения (т.е. по часовой стрелке).

Представив потокосцепление ротора по (69.30) как сумму соб-

ственного потокосцепления и взаимного потокосцепле-

ния в виде и заметив, что состав-

∼

12m

∼

+=Ψ

∼

12m

∼

---------

Im Ψ

∼

–()

---------------------------------------------------

---------

Im Ψ

∼

–()

---------------------------------------------------

∼

21m

∼

– jα

=Ψ

∼

433

ляющая электромагнитного момента по (69.44) от взаимодействия то-

ка с собственным потокосцеплением равна нулю

= 0,

можно выразить электромагнитный момент ротора через взаимное

потокосцепление

. (69.46)

Аналогично, представив потокосцепление статора по (69.29)

как сумму собственного и взаимного потокосцеплений

(в виде ), можно выразить электро-

магнитный момент статора по (69.45) через взаимное потокосцепле-

ние

(69.47)

и убедиться, что он не отличается от электромагнитного момента,

действующего на ротор.

Выразив в полученных уравнениях результирующие комплексы

токов и их сопряженные значения через фазные токи по (69.22),

(69.24), удостоверимся в том, что рассчитанный по (69.44), (69.46)

электромагнитный момент получается таким же, как момент, рассчи-

танный с помощью общего уравнения (69.21):

∼

–()

-------------------------------------------------------

–()

---------------------------------------------------------

∼

---------

Im Ψ

∼

–()

-------------------------------------------------------

== =

–

– jα

jα

–()

--------------------------------------------------------------------------------

∼

12m

∼

jα

= Ψ

∼

---------

Im Ψ

∼

–()

-------------------------------------------------------

== =

– jα

jα

–()

--------------------------------------------------------------------------------

---

Im Ψ

∼

– jα

jα

–()

--------------------------------------------------------------------------------

== =

– p

sin i

sin++()+=

434

В заключение приведем формулы для электромагнитного момента

через составляющие токов и потокосцеплений в осях d, q

(69.48)

или через составляющие токов и потокосцеплений в осях α, β

. (69.49)

69.10. Уравнения трехфазной асинхронной машины

в становившемся симметричном режиме

В установившемся симметричном режиме угловая скорость рото-

ра ω = p

Ω постоянна, а все электрические величины содержат только

составляющие прямой последовательности. Величины прямой после-

довательности статора, например токи прямой последовательности в

фазах статора, определяются выражениями:

;

в которых , — соответственно

комплексная функция и комплексная амплитуда тока прямой после-

довательности фазы A; ω

= 2π f

— угловая частота токов статора;

— фазовый угол для тока фазы А.

Вводя эти выражения в уравнения для результирующей комплекс-

ной функции тока статора в собственных осях α, β (69.22), получаем

sin i

sin++()++

sin i

sin++()]+=

– p

sin

nabc,,=

∑

k ABC,,=

∑

---

Im Ψ

∼

---

–()==

---

Im Ψ

∼

---

1α

1β

1α

–()==

Re I

∼

0,5 I

∼

+()==

Re I

∼

–

0,5 I

∼

–

∼

–

+()==

Re I

∼

–

0,5 I

∼

–

∼

–

+()==

∼

–

jω

= I

–

jβ

∼

1αβ

2 i

–

++()/3==

[ I

∼

1 a

–

++()I

∼

1 a

–

++()+ ]/3=

435

откуда

. (69.50)

Аналогично выражаются другие результирующие комплексы ста-

тора в осях α, β:

; , (69.51)

где ; ; η

и ϕ

— фазовые

углы для потокосцепления и напряжения фазы А.

Учитывая, что величины прямой последовательности ротора изме-

няются с угловой частотой ω

= ω

– ω = sω

, где ω

— угловая ско-

рость поля, получаем результирующие комплексы роторных величин

в осях d, q:

;;

, (69.52)

где ; ; ; β

, η

, ϕ

— фазо-

вые углы.

Для того чтобы записать уравнения установившегося режима в

осях, вращающихся с синхронной скоростью ω

, воспользуемся урав-

нениями (69.41), (69.42), пригодными для произвольной угловой ско-

рости осей ω

, положив в них ω

= ω

, α

= α

= ω

t и α = ωt:

;

и выразим все комплексные функции по (69.50), (69.51), (69.52) в этих

осях:

;;

; ;

; .

∼

1αβ

∼

–

jω

∼

1αβ

∼

–

jω

== U

∼

1αβ

∼

–

jω

–

jη

== U

–

jϕ

∼

2dq

∼

–

jω

== Ψ

∼

2dq

∼

–

jω

∼

2dq

∼

–

jω

–

jβ

=Ψ

–

jη

= U

–

jϕ

∼

p Ψ

∼

jω

∼

++=

∼

p Ψ

∼

j ω

ω–()Ψ

∼

++=

∼

1αβ

– jα

–

==Ψ

∼

1αβ

– jα

–

∼

1αβ

– jα

–

==I

∼

2dq

– j α

α–()

–

∼

2dq

– j α

α–()

–

==U

∼

2dq

– j α

α–()

–

436

Поскольку токи и потокосцепления в синхронных осях получи-

лись не зависящим от времени, производные потокосцеплений равны

нулю ( = 0, = 0). Это позволяет записать уравнения напря-

жений для установившегося режима в окончательном виде

; , (69.53)

где все величины выражены в синхронных осях и представляют собой

комплексные амплитуды.

Выразим теперь потокосцепления в (69.53) через токи с помощью

(69.29), (69.30):

(69.54)

где — комплексная амплитуда намагничивающего

тока, и разделим уравнение ротора на и на скольжение s = (ω

–

– ω)/ω

= ω

/ ω

, а уравнение статора на . В результате получим

систему уравнений:

(69.55)

полностью совпадающую с (41.11) для асинхронной машины, приве-

денной к трансформатору.

В этом можно убедиться, вспомнив, что =

= ; X

= ω

1σ

; X

= ω

2σ

; X

= ω

12m

; .

При этом нужно иметь в виду, что в (69.55) не учитываются магнит-

ные потери (R

= 0), а все роторные величины приведены к обмотке

статора (индексы приведения опущены).

∼

–

jω

–

+= U

–

jsω

–

12m

–

+ L

1σ

–

12m

–

;+==

–

12m

–

+ L

2σ

–

12m

–

,+==

⎭

⎬

⎫

–

jω

1σ

+()jω

12m

–

;+=

–

------

–

------

jω

2σ

⎝⎠

⎛⎞

jω

12m

–

+ 0,==

⎭

⎪

⎬

⎪

⎫

------

1 s–

------------

мех

+ E

–

– jX

–

437

Глава семидесятая

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В АСИНХРОННЫХ МАШИНАХ

70.1. Особенности переходных процессов в асинхронных

машинах

Анализ переходных процессов в асинхронных машинах наиболее

удобно проводить в комплексной форме по системе уравнений напря-

жений, записанных в осях d, q (69.32), (69.38), α, β (69.31), (69.34) или

в общем случае в комплексной плоскости, вращающейся с произволь-

ной скоростью ω

(69.41), (69.42). Эта система уравнений вместе с

уравнениями для напряжений нулевой последовательности u

и u

(69.19), (69.20) исчерпывающим образом (в пределах принятых допу-

щений) описывает симметричные и несимметричные установившие-

ся и переходные процессы в асинхронных машинах и может приме-

няться вместо системы уравнений для фазных напряжений (69.1)—

(69.4). Однако в отличие от системы уравнений для фазных напряже-

ний (69.1), (69.2) эта система уравнений значительно проще по своей

структуре и представляет собой совокупность линейных дифферен-

циальных уравнений с постоянными коэффициентами, что делает

возможным ее решение аналитическими методами и существенно

облегчает решение с помощью аналоговых или цифровых вычисли-

тельных машин. Уместно напомнить, что коэффициенты при токах

, R

, L

12m

, L

, ω) в уравнениях напряжений в осях α, β,

0 или d, q, 0 можно считать постоянными при допущениях о пренеб-

режении: насыщением стальных участков магнитной цепи; наличием

пазов у сердечников; высшими и низшими пространственными гар-

моническими составляющими магнитного поля (учитываются при-

ближенно только при расчете дифференциального рассеяния); выс-

шими гармоническими составляющими токов; магнит-

ными потерями и дополнительными потерями от вихревых токов в

проводниках; изменением угловой скорости (т.е. при условии ω =

= const).

Перед решением системы комплексных уравнений напряжений, за-

писанных в тех или иных осях, необходимо преобразовать к этим осям

как фазные величины, определяющие начальные условия, так и вели-

чины, изменение которых вызывает переходный процесс. Это может

временными

′

438

быть сделано с помощью уравнений типа (69.25), (69.27) или (69.26),

(69.28), а в наиболее общем случае (69.43). По найденным в результате

решения комплексным функциям токов с помощью обратного преобра-

зования определяются фазные токи. Например, если токи определены

в системе осей α, β, 0 и равны , = , то

;;;

;;

В большинстве переходных процессов ротор асинхронной маши-

ны замкнут накоротко и напряжение на выводах его трехфазной об-

мотки равно нулю ( = 0). Если в цепь обмотки ротора включена

симметричная система активных сопротивлений и индуктивностей,

то можно, добавив эти активные сопротивления к собственным ак-

тивным сопротивлениям ротора и индуктивностям рассеяния ротора,

считать напряжение на выводах обмотки ротора по-прежнему рав-

ным нулю ( = 0).

Приведенное в гл. 69 математическое описание может быть рас-

пространено и на асинхронные машины с короткозамкнутой обмот-

кой на роторе. Для этого достаточно многофазную короткозамкнутую

обмотку ротора заменить эквивалентной трехфазной обмоткой,

имеющей те же обмоточные данные, что и обмотка статора, и взять

параметры этой обмотки равными приведенным к обмотке статора

параметрам короткозамкнутой обмотки (см. § 40.4).

При исследовании переходных процессов, в которых скорость из-

менения частоты вращения соизмерима со скоростью изменения

электрических величин (т.е. процессов, называемых электромехани-

ческими), комплексные уравнения напряжений, записанные в тех или

иных осях, должны рассматриваться совместно с уравнением движе-

ния ротора (69.11). Электромагнитный момент в уравнении движения

вычисляется с помощью (69.48) или (69.49).

70.2. Переходные процессы при разомнтой обмоте

статора. Отлючение асинхронной машины от сети

Предположим, что до отключения машина работала в установив-

шемся режиме при угловой скорости ротора ω и частоте сети ω

. При

t = 0 происходит одновременное отключение всех фаз обмотки ста-

тора от сети и ток статора предшествующего установившегося режи-

∼

1α

1β

+= I

∼

2 αβ()

2α

2β

Re I

∼

= i

Re [ I

∼

–

]= i

Re [ I

∼

–

Re [ I

∼

2 αβ()

– jα

]= i

Re [ I

∼

2 αβ()

– jα

–

Re [ I

∼

2 αβ()

– jα

–

∼

439

ма весьма быстро (в течение времени горения дуги между

контактами, размыкающими цепь обмотки статора) обращается в

нуль. Считая короткозамкнутую обмотку ротора для этого проме-

жутка времени сверхпроводящей и применяя к ней принцип посто-

янства потокосцеплений, заключаем, что потокосцепление ротора

после исчезновения тока статора остается таким же,

как в предшествующем установившемся режиме при t = 0, когда оно

равнялось , где — ток ротора

предшествующего установившегося режима.

Эти потокосцепления могут быть выражены в любой системе осей

по (69.43а), причем здесь и в дальнейшем для упрощения записи

индуктивность взаимной индукции L

12m

обозначается L

без допол-

нительного индекса m. Из условия найдем ток ротора

после исчезновения тока статора

,(70.1)

где k

= L

— коэффициент связи ротора.

Дальнейший переходный процесс заключается в затухании тока

, начальное значение которого равно . Поскольку время горе-

ния дуги очень мало, можно считать, что этот процесс начинается при

t = 0. Ток определяется из уравнения для короткозамкнутой обмот-

ки ротора при разомкнутой обмотке статора, т.е. при = 0; = 0.

Запишем уравнение ротора (69.42) в системе осей, вращающихся с

произвольной скоростью ω

,где .

Решение этого однородного дифференциального уравнения =

= . Коэффициент затухания p

является корнем соответствую-

щего характеристического уравнения

∼

1 t 0=()

∼

2н

∼

2н

∼

2 t 0=()

∼

2 t 0=()

∼

1 t 0=()

+= I

∼

2 t 0=()

∼

2н

∼

2 t 0=()

∼

2н

∼

2 t 0=()

--------------------

∼

2 t 0=()

∼

1 t 0=()

+==

∼

2н

∼

[pjω

ω–()] Ψ

∼

++ 0=Ψ

∼

–

j ω

ω–()

--------

++0=