Иванов-Смоленский А.В. Электрические машины т 2

Подождите немного. Документ загружается.

420

В последнем можно убедиться c помощью (69.6)—(69.9), имея в

виде, что

где = . Это означает, что системы токов нулевой последова-

тельности образуют только поля рассеяния и не образуют основных

гармонических полей взаимной индукции. Именно поэтому L

<< L

По той же причине токи нулевой последовательности не принимают

участия в образовании электромагнитного момента и он может быть

выражен только через составляющие токов i

, i

, не со-

держащие токов нулевой последовательности [в этом можно убедиться,

представив токи в (69.13) в виде суммы двух составляющих]:

Имея в виду, что L

= L

cos α

, где α

= α + Δα

, причем α =

= p

γ, Δα

≠ f (γ), момент можно выразить через токи и углы α

меж-

ду фазами [см. (69.9)]

. (69.21)

69.3. Выражение фазных величин через резльтирющие

омплесные фнции

В теории установившихся режимов используются комплексы,

проекции которых на оси фаз изображают фазные величины прямой

последовательности (см. § 25.3). По аналогии с этим при исследова-

нии переходных процессов фазные величины, не содержащие состав-

ляющих нулевой последовательности, можно выразить через так на-

зываемые результирующие комплексные функции. Покажем, как оп-

ределяется результирующая комплексная функция тока статора.

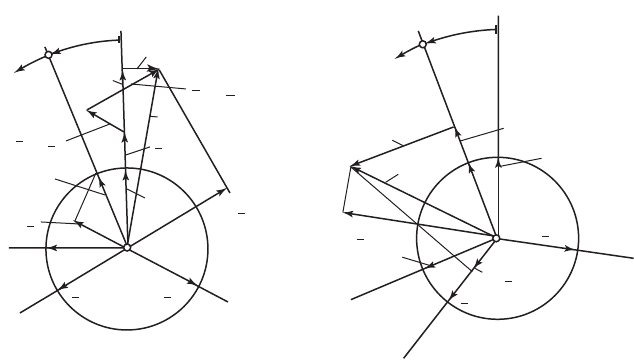
Введем комплексную плоскостность α, β, неподвижную относи-

тельно статора однопериодной модели (рис. 69.2). Совместим ее дей-

ствительную ось α с осью фазы А статора. Тогда единичные комплек-

сы = и совпадут соответственно с направлениями осей

cos α

cos++=

Re е

jα

++()Re[e

jα

1 a

–

++()]0===

–

j2π/3

k ABC,,=

∑

dγ

------------

nabc,,=

∑

M – p

k ABC,,=

∑

sin

nabc,,=

∑

–

j2π/3

–

421

фаз В и С и единичный комплекс , где α

= p

γ, укажет направ-

ление оси фазы а ротора. Результирующая комплексная функция тока

статора выражается через мгновенные значения токов фаз

, (69.22)

ее графическое определение показано на рис. 69.2.

Из рисунка видно, что проекции результирующей комплексной

функции тока на оси фаз равны соответствующим фазным токам. В

этом можно убедиться и аналитически. Проекция комплексной функ-

ции на произвольное направление = равна:

, (69.23)

где = . Поэтому проекция комплексной функции тока , на-

пример, на ось фазы В или на направление = , вычисленная по

(69.23), действительно (при выполнении условия i

+ i

= 0)

равна мгновенному току этой фазы

a, d

a,d

A, C

A,C

= i

2с

–jC

= i

Рис. 69.2. Результирующие комплексные функции токов статора и ротораI

∼

jα

∼

---

–

++()=

∼

jϕ

= s

–

jϕ

–()cos Re[ I

∼

–

]

–

--------------------------------

–

– jϕ

∼

–

j2π/3

Re[ I

∼

–

]Re[2i

–

++()a

–

/3()]==

2[i

Re a

–

()i

Re a

–

()]++ /3 i

422

При этом следует иметь в виду, что , = 1, =

= = –1/2. Таким же образом можно доказать, что проекции

комплексной функции на оси других фаз не отличаются от соответст-

вующих фазных токов

Аналогичным образом выражаются через фазные величины ре-

зультирующие комплексные функции напряжения и потокосцепле-

ния статора

;

Их проекции на оси фаз статора также не отличаются от соответ-

ствующих фазных величин.

Результирующие комплексные функции величин фаз ротора выра-

жаются во вращающейся комплексной плоскости d, q, неподвижной

относительно ротора однопериодной модели (см. рис. 69.2). Действи-

тельная ось d этой комплексной плоскости совмещается с осью фазы

а ротора. Тогда единичные комплексы и совпадут соответствен-

но с направлением осей фаз b и c, и единичный комплекс , где

= p

γ, укажет положение неподвижной оси фазы А статора.

Результирующие комплексные функции тока, напряжения и пото-

косцепления ротора выражаются через соответствующие фазные ве-

личины ротора

(69.24)

Их проекции на оси фаз равны соответствующим фазным величи-

нам, например ; и т.д.

–

= a

–

Re a

–

()

Re a

–

()

Re[ I

∼

æ 1] i

= Re[ I

∼

–

]Re[I

∼

–

] i

∼

2 u

–

++()/3=

∼

2 Ψ

–

++()/3=

–

– jα

∼

---

–

++();=

∼

---

–

++();=

∼

---

–

++().=

⎭

⎪

⎬

⎪

⎫

Re[ I

∼

–

] i

= Re[ U

∼

æ 1] u

423

69.4. Составляющие статорных величин в осях a, b

и роторных — в осях d, q

Результирующие комплексы статорных величин можно предста-

вить в виде суммы составляющих по направлениям осей α и jβ. На-

пример, результирующая комплексная функция тока статора по

(69.22) равна сумме токов i

1α

и ji

1β

, (69.25)

в которой

;

— составляющие тока статора соответственно по осям α и β.

Токи i

1α

и i

1β

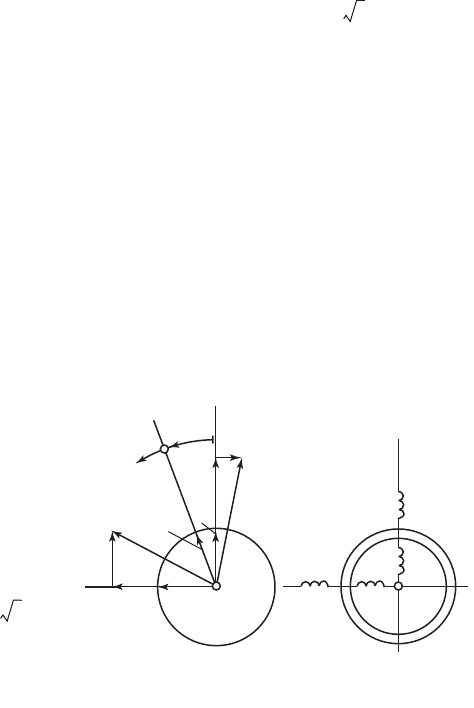
могут мыслиться как токи, протекающие по непод-

вижной двухфазной обмотке lα, 1β, оси фаз которой ориентированы

вдоль осей комплексной плоскости α, β (см. рис. 69.2, 69.3). Двухфаз-

ная обмотка lα, 1β с токами i

1α

, i

1β

(рис. 69.3) эквивалентна трехфаз-

ной обмотке статора A, B, C с токами i

, i

(см. рис. 69.1).

Результирующие комплексы роторных величин могут быть пред-

ставлены в виде составляющих по направлениям вращающихся осей

d и jq. Покажем, например, как найти составляющие результирующе-

го комплекса тока ротора по направлениям осей d, jq.

В этой комплексной плоскости ток ротора изображается по

(69.24) комплексом

, (69.26)

в котором

;

— составляющие тока

ротора соответственно

по осям d и q.

∼

1α

1β

1α

Re I

∼

+()/2 i

== =

1β

Im I

∼

–()/2j() i

–()/3== =

Re I

∼

+()/2 i

Im I

∼

–()/2j()==

–()/3=

j C

Рис. 69.3. Составляющие статорных и роторных

величин в неподвижных осях α, β

424

Токи i

и i

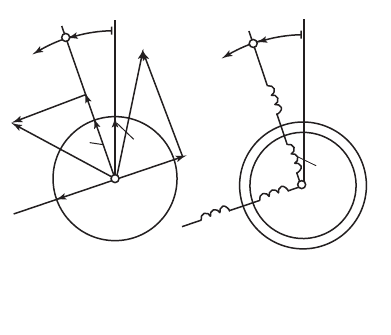
могут мыс-

литься как токи, проте-

кающие по вращающейся

двухфазной обмотке 2d,

2q, оси фаз которой ориен-

тированы вдоль осей ком-

плексной плоскости d, q

(см. рис. 69.2, 69.4). Вра-

щающаяся двухфазная об-

мотка 2d, 2q с токами i

(рис. 69.4) эквивалентна

трехфазной обмотке рото-

ра a, b, c с токами i

, i

(см. рис. 69.1).

Аналогично могут быть записаны формулы для потокосцеплений

и напряжений.

69.5. Составляющие статорных величин в осях d, q

и роторных — в осях a, b

Для записи уравнений в комплексной плоскости α, jβ не только

результирующие комплексные функции статорных величин, но и

результирующие комплексные функции роторных величин необходи-

мо представить в виде составляющих по направлениям осей α и jβ.

Покажем, как это сделать, на примере комплексной функции тока ро-

тора , которая во вращающейся плоскости d, jq определяется урав-

нением (69.26). Поскольку комплексная плоскость d, jq повернута на

угол α = α

относительно неподвижной комплексной плоскости α, jβ

(см. рис. 69.2), ток ротора в плоскости α, jβ изображается комплекс-

ной функцией

. (69.27)

Составляющие комплексной функции тока ротора по осям α и β

2α

= Re[(i

+ ji

jα

] = i

cos α – i

sin α;

2β

= Im[(i

+ ji

jα

] = i

sin α + i

cos α

представляют собой токи в двухфазной неподвижной обмотке 2α, 2β,

(см. рис. 69.3), образующей такое же магнитное поле, как вращаю-

щаяся двухфазная обмотка с токами i

, i

∼

2 αβ,()

∼

jα

+()e

jα

2α

2β

+== =

–jC

Рис. 69.4. Составляющие статорных и ротор-

ных величин во вращающихся осях d, q

425

Аналогичное преобразование делается с результирующими ком-

плексными функциями статорных величин при записи уравнений во

вращающейся комплексной плоскости d, jq. Например, если в непод-

вижной комплексной плоскости α, jβ ток статора изображался по

(69.26) комплексной функцией , то в комплексной

плоскости d, jq, повернутой на угол –α = – α

относительно плоскости

α, jβ (см. рис. 69.2), этот ток изображается комплексной функцией

. (69.28)

Составляющие комплексной функции тока статора по осям d и q

= Re[(i

1α

+ ji

1β

–jα

] = i

1α

cos α + i

1β

sin α;

= Im[(i

1α

+ ji

1β

–jα

] = – i

1α

sin α + i

1β

cos α

представляют собой токи в двухфазной вращающейся обмотке 1d, 1q

(см. рис. 69.4), образующей такое же магнитное поле, как неподвиж-

ная двухфазная обмотка с токами i

1β

, i

2β

. Аналогично могут быть

записаны формулы для потокосцеплений и напряжений статора в осях

d, q и для потокосцеплений и напряжений ротора в осях α, β.

69.6. Выражение резльтирющих омплесных фнций

потоосцеплений через резльтирющие омплесные

фнции тоов

Потокосцепления фаз статора Ψ

, Ψ

в (69.20) могут быть

выражены с помощью (69.20), (69.9) через фазные токи, индуктив-

ность фазы статора L

и взаимные индуктивности между фазами ро-

тора и статора

= L

cos α;

;

и т.д., которые зависят от углового положения ротора, электрического

угла между осями фазы А статора и фазы а ротора α = α

= p

γ.

∼

1α

1β

∼

1 dq()

∼

– jα

1α

1β

+()е

– jα

+== =

2π

-----

⎝⎠

⎛⎞

cos=

4π

-----

⎝⎠

⎛⎞

cos=

4π

-----

⎝⎠

⎛⎞

cos=

426

Представляя косинусы углов между фазами в показательной форме

через единичные комплексы , , , =

= , указывающие направление осей фаз на рис. 69.2, и обраща-

ясь к уравнениям для результирующих комплексных функций токов

статора и ротора (69.22), (69.24), легко доказать, что результирующая

комплексная функция потокосцепления статора выражается через ре-

зультирующие комплексные функции токов статора и ротора

, (69.29)

где L

12m

= 3L

/2 — главная взаимная индуктивность между фазой

статора и фазами ротора (см. § 28.4); — результирую-

щая комплексная функция тока ротора, выраженная в неподвижной

комплексной плоскости статора α, β (см. рис. 69.2).

Аналогично с помощью (69.9), (69.20), (69.22), (69.24) и таких же

подстановок можно доказать, что и результирующая комплексная

функция потокосцепления ротора выражается через результирующие

комплексные функции токов статора и ротора и соответствующие ин-

дуктивности

, (69.30)

где — результирующая комплексная функция тока

статора, выраженная во вращающейся комплексной плоскости рото-

ра d, q (см. рис. 69.2).

69.7. Уравнения напряжений в осях a, b

Для того чтобы перейти от системы из трех уравнений напряжений

для отдельных фаз статора (69.18) к уравнению, записанному через

результирующие комплексные функции, нужно умножить уравнение

для u

на 2/3, уравнение для u

— на 2а/3, уравнение для u

— на

αcos Re e

–

----------------

2π

-----

⎝⎠

⎛⎞

cos Re e

–

-------------------------

4π

-----

⎝⎠

⎛⎞

cos Re e

–

-------------------------

–

jα

= e

–

– jα

= a

–

2π

------

= a

–

j4π/3

∼

12m

∼

jα

+ L

∼

12m

∼

2 αβ()

+==

∼

2 αβ()

∼

jα

∼

12m

∼

– jα

+ L

∼

12m

∼

1 dq()

+==

∼

1 dq()

∼

– jα

427

2а

/3 и сложить почленно правые и левые части этих уравнений. В ре-

зультате такого сложения, учитывая (69.22), (69.23), получаем уравне-

ние напряжений статора в собственной комплексной плоскости α, β

, (69.31)

в котором результирующая комплексная функция потокосцепления

статора выражается через токи c помощью (69.29). Поступая таким

же образом с системой из трех уравнений напряжений для отдельных

фаз ротора (69.18), получаем (после умножения уравнения для u

на

2/3, для u

— на 2а/3, для u

— на 2a

/3 и почленного сложения их

правых и левых частей) уравнение напряжений ротора в собственной

комплексной плоскости d, q

, (69.32)

в котором результирующая комплексная функция потокосцепления

ротора выражается через токи с помощью (69.30).

Однако уравнения для и , записанные в различных ком-

плексных плоскостях, не могут быть решены совместно. Поэтому од-

но из этих уравнений, в данном случае уравнение для , должно

быть преобразовано и записано через комплексные функции ,

, , выраженные в системе координат α, β. Как вытекает

из (69.27),

;; ,

где α = α

= α(t) — угол между осями фаз статора и ротора (по

рис. 69.2).

После указанной подстановки (69.32) приобретает вид:

При взятии производной нужно учитывать, что α = α

— угол ме-

жду осями фаз статора и ротора по рис. 69.2 изменяется во времени

α=α(t)

∼

d Ψ

∼

----------

∼

d Ψ

∼

----------

∼

2 αβ()

∼

2 αβ()

∼

2 αβ()

∼

2 αβ()

– jα

= I

∼

2 αβ()

– jα

=Ψ

∼

2 αβ()

– jα

∼

2 αβ()

– jα

∼

2 αβ()

– jα

-----

[ Ψ

∼

2 αβ()

– jα

]+=

∼

2 αβ()

– jα

∼

2 αβ()

– jα

d Ψ

∼

2 αβ()

---------------------

∼

2 αβ()

– je

– jα

dα

------

⎝⎠

⎛⎞

++=

428

Разделив все члены уравнения на e

–jα

и имея в виду, что dα/dt =

=ω — электрическая угловая скорость ротора, получим уравнение

напряжений ротора

, (69.33)

в котором все величины выражены в неподвижной комплексной плос-

кости α, β. Это относится, конечно, и к потокосцеплению. Оно вычис-

ляется по формуле, вытекающей из (69.27), (69.28)—(69.30):

в которую входят комплексы токов, выраженные в плоскости α, β.

Договорившись заранее, что все величины отнесены к комплекс-

ной плоскости α, β, можно записать уравнение напряжений ротора

без индексов (α, β)

, (69.34)

где .

Если все комплексные величины в (69.31) и (69.34) выразить с по-

мощью (69.25), (69.27) через составляющую по осям α, β, то вместо

пары уравнений напряжений в комплексной форме появятся четыре

уравнения в скалярной форме (соответственно для напряжений u

1α

1β

, u

2α

, u

2β

(69.35)

Составляющие потокосцеплений в этих уравнениях выражаются

через соответствующие составляющие токов

(69.36)

∼

2 αβ()

∼

2 αβ()

d Ψ

∼

2 αβ()

---------------------

jωΨ

∼

2 αβ()

–+=

∼

2 αβ()

∼

jα

∼

jα

12m

∼

1 dq()

jα

+ L

∼

2 αβ()

12m

∼

+== =

∼

d Ψ

∼

----------

jωΨ

∼

–+=

∼

12m

∼

1α

dΨ

1α

--------------

+= ; u

1β

dΨ

1β

--------------

;+=

2α

dΨ

2α

--------------

ωΨ

2β

++= ; u

2β

dΨ

2β

--------------

ωΨ

2α

–.+=

⎭

⎪

⎬

⎪

⎫

1α

12m

2α

;+=

2α

12m

1α

;+=

1β

12m

2β

;+=

2β

12m

1β

.+=

⎭

⎬

⎫

429

69.8. Уравнения напряжений в осях d, q и в осях,

вращающихся с произвольной соростью.

Эвивалентные схемы замещения

В этом случае в преобразовании нуждается только уравнение на-

пряжений статора (69.31). Все величины, которые в него входят, вы-

ражаются в комплексной плоскости d, q c помощью уравнений вида

(69.28)

Учитывая при взятии производной, что α = α(t) является функцией

времени

и сокращая все члены уравнения e

jα

, получаем уравнение напряже-

ний статора

, (69.37)

в котором все величины выражены во вращающейся комплексной

плоскости d, q. Потокосцепление по (69.27)—(69.29) также представ-

ляется как функция токов, выраженных в плоскости d, q:

Часто индексы d, q в уравнении (69.37) опускают, делая оговорку,

что оно записано в комплексной плоскости d, q

. (69.38)

где .

Для представления системы комплексных уравнений (69.32) и

(69.38) в скалярной форме нужно выразить все комплексные величи-

ны, которые в них входят, через проекции на оси d и q по (69.26),

(69.28) и приравнять отдельно действительные и мнимые составляю-

щие правых и левых частей уравнений. Это дает возможность запи-

сать систему из четырех уравнений для составляющих напряжений

∼

1 dq()

jα

∼

1 dq()

jα

-----

[ Ψ

∼

1 dq()

jα

]+=

∼

1 dq()

jα

∼

1 dq()

jα

d Ψ

∼

1 dq()

--------------------

∼

1 dq()

jα dα

------

⎝⎠

⎛⎞

++=

∼

1 dq()

∼

1 dq()

d Ψ

∼

1 dq()

--------------------

jωΨ

∼

1 dq()

++=

∼

1 dq()

∼

– jα

∼

– jα

12m

∼

2 αβ()

– jα

+ L

∼

1 dq()

12m

∼

+== =

∼

d Ψ

∼

----------

jωΨ

∼

++=

∼

12m

∼