Ирхин В.Ю., Ирхин Ю.П. Электронная структура, корреляционные эффекты и физические свойства d - и f-переходных металлов и их соединений
Подождите немного. Документ загружается.


энергетические знаменатели заменяются резольвентами и сооответствующие состо-
яния имеют неквазичастичную природу. Подобная ситуация имеет место в прибли-
жении Хаббард-III [30,694,695], где затухание на уровне Ферми конечно (см. (H.17),
(J.24)).
Рассмотрим модель Хаббарда с U → ∞, n = 1−c < 1 (c = N
0
= n
0
- концентрация
дырок, N
2
= 0) с включением внешнего магнитного поля (4.96). В приближении
Хаббард-I мы получаем функции Грина
hhX
k
(σ0)|X
−k
(0σ)ii
E
=
c + n
σ
E − τ
kσ
− σH/2
(H.11)
τ
kσ
= (c + n
σ
)ε
k
= [(1 + c)/2 + σhS
z
i]ε
k
и, с учетом спектрального представления (E.18), соответствующие выражения для
чисел заполнения
n
kσ
≡ hX
−k
(0σ)X
k
(σ0)i =
µ
1 + c
2
+ σhS
z
i
¶
f(τ
kσ
+
1
2
hσ) (H.12)
В принципе уравнения (H.4), (H.5) могут быть использованы для исследования
магнитного упорядочения в модели Хаббарда. Однако приближение Хаббард-I в этой
проблеме неудовлетворительно, так как трудно сформулировать разумный критерий
ферромагнетизма с непосредственным использованием выражений для одноэлек-
тронных функций Грина типа (H.4), (H.11). Первая такая попытка была сделана
самим Хаббардом [28], который не нашел магнитных решений для простых затра-
вочных плотностей состояний (однако ситуация может измениться в случае вырож-
денных d-зон [696]). Метод X-операторов проясняет причину этой неудачи: можно, в
частности, видеть, что приближение (H.11) нарушает книматические сооотнношения
(A.25), так как при hS
z
i 6= 0 невозможно удовлетворить тождества
X
k
n
kσ
= hX(00)i = c (H.13)
для обеих проекций спина σ. Кроме того, подходы стонеровского типа не описыва-
ют образование локальных моментов и физически неудовлетворительны. Поэтому в
разделе 4.5 используется подход на основе спиновой функции Грина
G
q
(
ω
) =
hh
X
q
(+
−
)
|
X
−q
(
−
+)
ii
ω
=
hh
S
+
q
|
S
−
−q
ii
ω
(H
.
14)
Для ее вычисления запишем цепочку уравнений движения
(ω − H)G
q
(ω) = n
↑
− n
↓
+
X
k
(ε
k−q
− ε
k
) (H.15)
×hhX
q−k
(0−)X
k
(+0)|X
−q
(−+)ii
ω
(ω − τ
k↑
+ τ
k−q↑
− H)hhX
q−k
(0−)X
k
(+0)|X
−q
(−+)ii
ω
= n
k↑
− n
k−q↓
+ (ε
k−q
n
k−q↓
− ε
k
n
k↑
)G
q
(ω)
где мы выполнили простейшее расцепление, которое соответствует пренебрежению
флуктуациями чисел заполнения дырок. Подставляя (H.15) в (H.14), получаем вы-
ражение (4.97).
251

Флуктуационные поправки к электронным функциям Грина приближения
Хаббард-I были получены в работах [337,338] в рамках разложения по 1/z (z - чис-
ло ближайших соседей). Они выражаются через одночастичные числа заполнения
и спиновые и зарядовые корреляцилонные функции. В отличие от приближения
Хаббард-I такие выражения позволяют правильно получить магнитную фазовую
диаграмму и описать насыщенное и ненасыщенное ферромагнитное состояние [729].
Первая критическая концентрация носителей тока, соответствующая неустойчиво-
сти насыщенного ферромагнетизма, составляет для различных решеток около 30%.
Для парамагнитной фазы щель в спектре (H.8) сохраняется при сколь угодно
малых U. Чтобы описать переход металл-изолятор, который имеет место при U ∼
W (W - ширина зоны), требуются более сложные самосогласованные приближения
для электронных функций Грина. Первое описание такого типа было предложено
Хаббардом [30], а более простое приближение использовалось Зайцевым [697].
Выражение Хаббард-III для одноэлектронной функции Грина в случае наполо-
вину заполненной зоны может быть представлено в виде [695]
G
k
(E) = [E − t
k
− Σ(E)]
−1
(H.16)
причем электронная собственная энергия определяется самосогласованно через точ-
ную резольвенту:
Σ(E) =
U
2
16Ψ
R(E)/
·
1 + Σ(E)R(E) + ER(E)(
1
4Ψ
− 1)
¸
(H.17)
R(E) =
X
k
G
k
(E)
где Ψ = 3/4. Выражение (H.17) выполняется также для классической (S → ∞) s-d
обменной модели (см. Приложение I), если мы положим Ψ = 1/4, U → |IS|. Тогда
формула (H.17) упрощается и совпадает с результатом приближения когерентного
потенциала (CPA) в теории неупорядоченных сплавов [435]. ??Эволюция электрон-
ного спектра в зависимости от параметра взаимодействия показана на Рис.H1.
Некоторые недостатки приближений [30,697] (нарушение аналитических свойств
функций Грина, несамосогласованное описание термодинамических свойств) обсуж-
даются в работах [694,695] с точки зрения 1/z-разложения. Правильное описание
перехода Мотта-Хаббарда до сих пор является важной физической проблемой. В
последнее время здесь широко используется приближение бесконечной размерности
пространства d [705], которое дает трехпиковую структуру плотности состояний,
включая кондовский пик на уровне Ферми. Такой подход может давать два фазовых
перехода: при U > U
c1
нарушается фермижидкостная картина, а при U > U
c2
> U
c1
система переходит в изоляторное состояние. Учет фермиевских возбуждений в рам-
ках 1/z-разложения был выполнен в работе [730]. Использование локаторного пред-
ставления для функции Грина
G
k
(E) =
1
F (E) − t
k
(H.18)
252

позволило получить правильные аналитические свойства и воспроизвести трехпико-
вую структуру. Самосогласованные результат для локатора F (E) имеет вид
F (E) =
b(E)
a(E)
,
a(E) = 1 +
3
4
U
2
E
2
X
q
t
q
G
q
(E) +
2U
E
X
q
t
q
G
q
(E)n
q
,
b(E) = F
0
(E) +
2U
E
X
q
t
2
q
G
q
(E)n
q
.
где n
q
- точные числа заполнения.
Мы видели, что подходы Хартри-Фока и Хаббарда дают существенно разные
результаты для электронного спектра. Неадекватность одноэлектронного подхода
в случае больших U может быть показана рассмотрением случая малых электрон-
ных концентраций n [353]. Рассмотрим разложение одноэлектронной функции Гри-
на по числам заполнения носителей тока. В одноэлектронном представление (f
k
=
ha
†
kσ
a
kσ
i) получаем уравнение движения
(E − t
k
)hha
k↑
|a
†
k↑
ii
E
= 1 + U
X
k
1
k
2
F
k
(k
1
k
2
E) (H.19)
L
k
(k
1
k
2
E) = hha
†
k
1
↓
a
k
2
↓
a
k+k
1
−k
2
↑
|a
†
k↑
ii
E
В низшем порядке по f
k
получаем замкнутое интегральное уравнение
(E − t
k+k
1
−k
2
+ t
k
1
− t
k
2
)L
k
(k
1
, k
2
, E)
= δ
k
1
k
2
f
k
+ U(1 − f
k
2
)
X
p
L
k
(k, p,E)
Решая его, находим выражение для электронной собственной энергии
Σ
k
(E) = U
X
k
1
f
k
1
"
1 − U
X
k
2
(1 − f
k
2
)(1 − f
k+k
1
−k
2
)
E − t
k+k
1
−k
2
+ t
k
1
− t
k
2
#
−1
(H.20)
которая конечна при U → ∞ [348]. В то же время, согласно (E.18), (H.19) число
двоек
N
2
= ha
†
i↑
a
i↑
a
†
i↓
a
i↓
i = −
1
π
Z
dEf(E) Im
X
kk
1
k
2
L
k
(k
1
k
2
E) (H.21)
= −
1
πU
Z
dEf(E) Im
X
k
Σ
k
(E)
E − t
k
ведет себя в этом пределе как 1/U. Тогда теорема Геллмана-Фейнмана N
2
= ∂E/∂U
дает расходимость энергии основного состояния E:
E(U) − E(0) =
Z
∞
0
dUN
2
(U) ∼ ln U (H.22)
253

Эта расходимость указывает на фомирование хаббардовских подзон и неправиль-
ность одноэлектронной картины при больших U. С другой стороны, вычисление в
МЭ представлении дает [353]
hhX
k
(σ2)|X
−k
(2σ)ii
E
'
X
k
1
f
k
1
"
E + t
k
1
− U −
X
k
2
(t
k+k
1
−k
2
+ t
k
2
)
2
E − t
k+k
1
−k
2
+ t
k
1
− t
k
2
#
−1
(H.23)
так что
N
2
= −
1
π
Im
X
k
Z
dEf(E) ImhhX
k
(σ2)|X
−k
(2σ)ii
E
(H.24)
'
1
U
2
X
kk
1
k
2
(t
k+k
1
−k
2
+ t
k
2
)
2
f
k
1
f(t
k+k
1
−k
2
− t
k
1
+ t
k
2
)
'
n
2
U
2
t
min
Таким образом мы получаем правильную асимптотику N
2
∼ 1/U
2
.
254
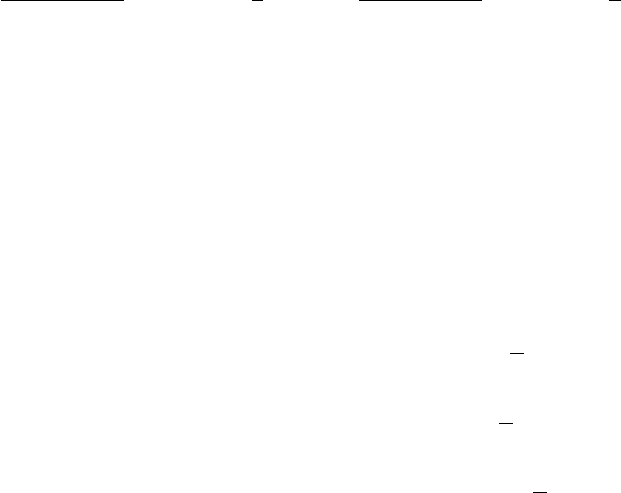
Приложение I
s-d обменная модель с узкими зонами
и t-J модель
При рассмотрении переноса электронов в узких вырожденных зонах, помимо модели
Хаббарда, можно использовать s-d обменную модель с сильными корреляциями. Эта
модель соответствует случаю, когда носители тока не принадлежат той же энерге-
тической зоне, в которой формируются магнитные моменты. Такая ситуация имеет
место в некоторых магнитных полупроводниках и изоляторах [668].
В отличие от вырожденной модели Хаббарда, стандартный гамильтониан s-d об-
менной модели (G.2) не включает орбитальных степеней свободы. В случае большо-
го s-d обменного параметра I удобно перейти к атомному представлению [698-700].
Подставляя значения коэффициентов Клебша-Гордана, отвечающих сложению мо-
ментов S и 1/2, мы находим собственные функции H
sd
|Mi ≡ |SMi|0i, |M2i ≡ |SMi|2i (I.1)
|µ±i =
µ
S ± µ + 1/2
2S + 1
¶
1/2
|S, µ −
1
2
i| ↑i ±
µ
S ∓ µ + 1/2
2S + 1
¶
1/2
|S, µ +
1
2
i| ↓i (I.2)
где |mαi - состояния, занятые одним электроном с полным спином на узлу S + α/2
и его проекцией m. Тогда H
sd
диагонализуется:
H
sd
= −IS
S+1/2
X
µ=−S−1/2
X
i
X
i
(µ+, µ+) + I(S + 1)
S−1/2
X
µ=−S+1/2
X
i
X
i
(µ−, µ−) (I.3)
Одноэлектронные операторы выражаются черех X-операторы как
c
†
iσ
=
X
α
(g
†
iσα
+ h
†
iσα
) (I.4)
g
†
iσ+
=
X
M
{(S + σM + 1)/(2S + 1)}
1/2
X
i
(M +
σ
2
, +; M)
g
+
iσ−
=
X
M
σ {(S − σM)/(2S + 1)}
1/2
X
i
(M +
σ
2
, −; M)
h
†
iσ+
=
X
M
{(S + σM)/(2S + 1)}
1/2
X
i
(M2; M −
σ
2
, −)
255
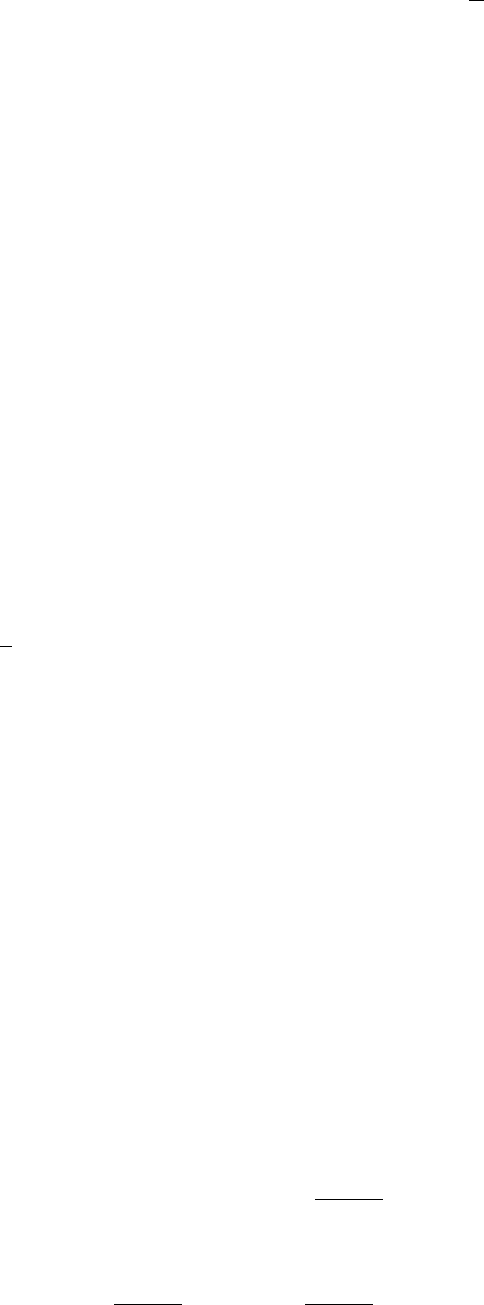
h
†
iσ+
=
X
M
σ {(S − σM + 1)/(2S + 1)}
1/2
X
i
(M2; M −
σ
2
, +)
В пределе I → α∞ для концентрации электронов проводимости n < 1 нужно сохра-
нить в (I.4) только члены, содержащие g
iα
, и опустить гамильтониан H
sd
, который
дает постоянный сдвиг энергии. Мы получаем
H =
X
kσ
t
k
g
†
kσα
g
kσα
+ H
d
, α = signI (I.5)
Для n > 1 мы должны сохранить члены, содержащие h
iα
и перейти к “дырочно-
му"представлению введением новых локализованных спинов
e
S = S ± 1/2 . Тогда
гамильтониан принимает вид (I.6) с заменой [700]
t
k
→ −t
k
([
e
S]/[S]) (I.6)
При теоретическом рассмотрении сильнокоррелированных соединений, например,
медь-кислородных высокотемпературных сверхпроводников, широко используется
t −J модель (модели Хаббарда для s-зоны с U → ∞ включением гейзенберговского
обмена). Ее гамильтониан в МЭ представлении имеет вид
H = −
X
ijσ
t
ij
X
i
(0σ)X
j
(σ0) −
X
ij
J
ij
{X
i
(+−)X
j
(−+) (I.7)
+
1
4
[X
i
(++) − X
i
(−−)] [X
j
(++) − X
j
(−−)]
¾
При получении t − J модели из модели Хаббарда с большим U имеем J = −4t
2
/U -
антиферромагнитный интеграл кинетического обмена. Впрочем, иногда удобно счи-
тать J независимой переменной. В частности, иногда исследуют “суперсимметрич-
ный“ случай с t = J [701], что позволяет использовать нетривиальные математиче-
ские методы.
Легко видеть, что модель (I.7) - частный случай s-d обменной модели с I →
−∞, S = 1/2, причем t
k
заменяется в (I.5) на 2t (множитель 2 возникает из-за
эквивалентности электронов с противоположными спинами в модели Хаббарда). s-d
модель с произвольным спином S иногда оказывается более удобной, так как она
использует при вычислениях, помимо малого параметра 1/z (z - число ближайших
соседей), квазиклассический параметр 1/2S. Квазиклассическая s-d модель с S À 1
в атомном представлении была использована для исследования перехода металл-
изолятор [695] (приложение H).
Гамильтониан (I.5), аналогично (C.33), может быть выражен через фермиевские
операторы и операторы локализованных спинов. Наконец, используя (A.21), (A.11),
мы можем выделить операторы электронов проводимости из X-операторов:
g
†
iσα
=
X
σ
0
c
†
iσ
0
(1 − n
i,−σ
0
)
·
P
α
δ
σσ
0
+
α
2S + 1
(S
i
σ
σσ
0
)
¸
(I.8)
где
P
+
=
S + 1
2S + 1
, P
−
=
S
2S + 1
(I.9)
256
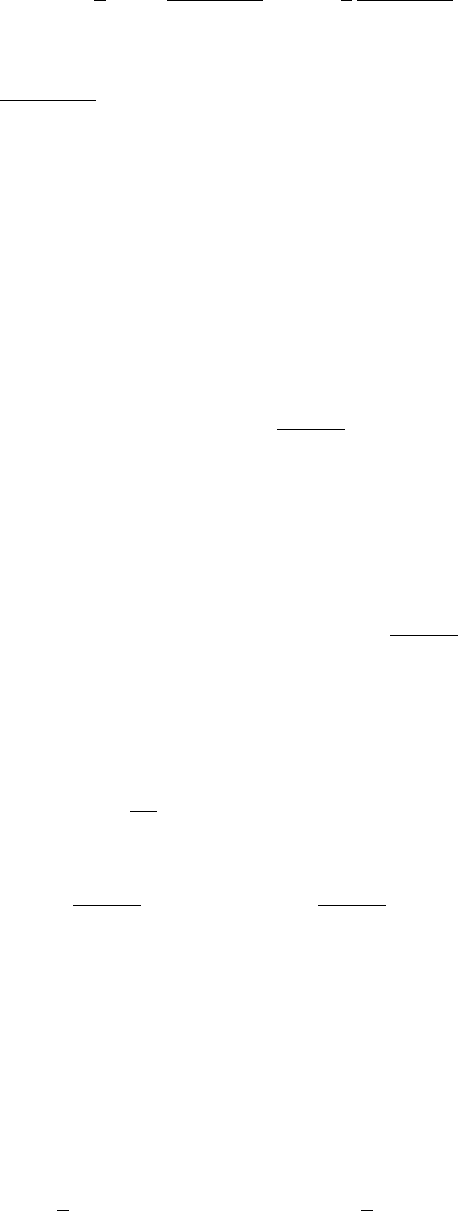
Кубо и Охата получили этот результат [702] с помощью канонического преобразова-
ния. Используя свойства матриц Паули, мы получаем
H =
X
ijσσ
0
t
ij
½
[
1
4
P
2
α
+
S
i
S
j
(2S + 1)
2
]δ
σσ
0
+
1
2
α
(2S + 1)
2
P
α
(S
i
+S
j
)σ
σσ
0
(I.10)
+
2i
(2S + 1)
2
σ
σσ
0
[S
i
×S
j
]
¾
c
†
iσ
(1 − n
i,−σ
)(1 − n
i,−σ
0
)c
jσ
0
+ H
d
Члены, содержащие векторные произведения (ср. (K.8)), описывают анизотропное
рассеяние электронов и могут быть важны при рассмотрении кинетических явлений
в узких зонах, например, аномального эффекта Холла. Гамильтониан (I.10) может
быть полезен при исследовании состояний с аномальными “ киральными“ парамет-
рами порядка, которые исследовались в рамках двумерной модели Гейзенберга и
t − J модели (см., например, [703]). Гамильтониан (I.5) более удобен при описании
простых приближений в рамках 1/z-разложения [694]. Выполняя простейшие рас-
цепления, мы получаем электронный спектр в ферромагнитной фазе
E
kσα
=
µ
P
α
−
ασ
2S + 1
hS
z
i
¶
t
k
(I.11)
Это выражение дает сильную зависимость электронного спектра от магнитного упо-
рядочения. Более точное выражение для функции Грина со спином вниз при α = +,
T = 0 [699] имеет неквазичастичную форму
hhg
k↓+
|g
†
k↓+
ii
E
=
"
E − t
k
− 2S(
X
q
1
E − t
q
)
−1
#
−1
(I.12)
Магнонный спектр в модели (I.5) был расчитан в [79,80,83]. Результат в низшем
порядке по 1/z имеет вид
ω
q
=
1
2S
X
k
(t
k−q
− t
k
)f(t
k
), α = + (I.13)
ω
q
=
1
2S + 1
X
k
(t
k−q
− t
k
)f(
2S
2S + 1
t
k
), α = −
В антиферромагнетике со спиральной магнитной структурой, соответствующей вол-
новому вектору Q, мы должны перейти в s −d гамильтониане к локальной системе
координат с использованием (E.8), (G.90). Далее, переходя от операторов d
†
iσ
к МЭ
операторам, мы получаем вместо (I.5)
H =
X
kσ
(θ
k
g
kσα
g
kσα
+ τ
k
g
kσα
g
k,−σ,α
) + H
d
(I.14)
τ
k
=
1
2
(t
k+Q/2
− t
k−Q/2
), θ
k
=
1
2
(t
k+Q/2
+ t
k−Q/2
)
257
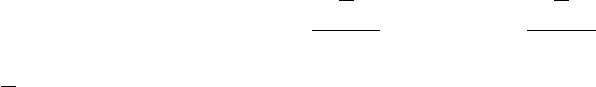
Выполняя расцепление “Хаббард-I”, мы получаем для электронного спектра [687]
E
1,2
k
= P
α
θ
k
±
½
(
S
2S + 1
θ
k
)
2
+ [P
2
α
− (
S
2S + 1
)
2
]τ
k
¾
1/2
(I.15)
где S - намагниченность подрешетки. В приближении ближайших соседей (θ
q
= 0)
для I > 0 зона при T = 0 сужается в (2S + 1)
1/2
раз. В то же время, в рассматривае-
мом приближении для I < 0 (а также в t−J модели) электроны не могут переходить
на соседние узлы, и их движение возможно только благодаря квантовым эффектам.
Эта проблема обсуждается в разделе 6.7.
Флуктуационные поправки к спектру обсуждаются в [687,620]. Результат для
магнонного спектра, полученный в МЭ представлении, совпадает с результатом обоб-
щенного приближения Хартри-Фока (G.95).
258
Приложение J
Электронные состояния и спиновые
волны в хаббардовском
ферромагнетике с узкими зонами
Электронный и магнонный спектры в хаббардовском ферромагнетике с сильным
корреляциями (U → ∞), который описывается гамильтонианом
H =
X
kσ
ε
k
X
−k
(0σ)X
k
(σ0) (J.1)
можно исследовать строго в случае малой концентрации дырок c = 1 −N
e
/N (почти
наполовину заполненная зона) и низких температур. Формально это достигается раз-
ложением по дырочным и магнонным числам заполнения [333,699,700]. Рассмотрим
одночастичные функции Грина
G
kσ
= hhX
k
(σ0)|X
−k
(0σ)ii
E
(J.2)
Используя коммутационные соотношения
[X
k
(+0), H] =
X
p
ε
k−p
{[X
p
(00) + X
p
(++)]X
k−p
(+0) + X
p
(+−)X
k−p
(−0)}
мы запишем для σ =↑ уравнение движения (E.16a)
(E − ε
k
)G
k↑
(E) = 1 − n
↓
+
X
pq
(ε
k−p
− ε
k+q−p
) (J.3)
×hhX
−q
(−+)X
p
(+−)X
k+q−p
(+0)|X
−k
(0+)ii
E
Здесь мы учли кинематические соотношения
X
p
(++) + X
p
(−−) = δ
p0
− X
p
(−−), X
p
(−−) =
X
q
X
−q
(−+)X
p+q
(+−), (J.5)
X
k−p
(−0) =
X
q
X
−q
(−+)X
k+q−p
(+0)
259

которые следуют из (A.28), (A.25), привели произведения операторов к “нормаль-
ной форме", где все операторы X(−+) стоят слева, сохраняя линейные по спиновым
отклонениям члены и пренебрегая вкладами, пропорциональными дырочной кон-
центрации. Вводя функции
ϕ
kqp
(E) = hhX
−q
(−+)X
p
(+−)X
k+q−p
(+0)|X
−k
(0+)ii
E
/ [(E − ε
k
)N
q
] (J.6)
где
N
q
= hX
−q
(−+)X
q
(+−)i
мы приходим тем же путем к замкнутому интегральному уравнению
(E − ε
k+q−p
)ϕ
kqp
(E) = (E − ε
k
)(δ
pq
− 1)+ (J.7)
X
r
(ε
k+q−p−r
− ε
k+q−r
)ϕ
kqr
(E)
которое описывает рассеяние дырок на магнонах. Записывая уравнение Дайсона
G
k↑
(E) =
1 − n
↓
E − ε
k
·
1 −
1
E − ε
k
Σ
k
(E)
¸
' (1 − n
↓
) [E − ε
k
− Σ
k
(E)]
−1
(J.8)
мы получаем для собственной энергии
Σ
k
(E) =
X
pq
(ε
k−p
− ε
k+q−p
)ϕ
kqp
(E) (J.9)
Магнонный спектр получается с помощью спиновой функции Грина. Уравнение
движения для нее имеет (ср. (H.15))
ωG
q
(ω) = 1 − c +
X
kp
(ε
k−p
− ε
k
) (J.10)
×hhX
−k
(0+)X
q−k+p
(+−)X
k
(+0)|X
−q
(−+)ii
ω
Выполняя вычисления при T = 0 в низшем порядке по числам заполнения магнонов
n
k
= hX
−k
(0+)X
k
(+0)i = f(ε
k
)
мы получаем магнонную собственную энергию. Она, как оказывается, определяется
той же функцией ϕ
G
q
(ω) = (1 − c)
"
ω −
X
kp
(ε
k−p
− ε
k+q−p
)ϕ
kqp
(ω + ε
k
)
#
−1
(J.11)
В низшем порядке по малому параметру 1/z (каждому порядку по 1/z соответствует
дополнительное суммирование по волновому вектору) мы получаем для температур-
ной поправки к электронному спектру и к магнонной частоте
δε
k
(T ) =
X
q
(ε
k−q
− ε
k
)N
q
(J.12)
260
