Ирхин В.Ю., Ирхин Ю.П. Электронная структура, корреляционные эффекты и физические свойства d - и f-переходных металлов и их соединений
Подождите немного. Документ загружается.


Можно строго показать, что энтропия взаимодействующей фермиевской системы
при низких T выражается через квазичастицы Ландау с энергиями, определенными
как вариационные производные полной энергии относительно чисел заполнения. Та-
ким образом, даже в присутствии неполюсных вкладов в функции Грина описание
термодинамики через статистические квазичастицы [685] сохраняется. (Однако опи-
сание через квазичастицы недостаточно для спектральных характеристик, напри-
мер, для оптических и эмиссионных данных.) Аномальный γT -член определяется
различием спектров статистических и динамических квазичастиц.
Подобные вклады в удельную теплоту в модели Хаббарда с сильными корреляци-
ями обсуждаются также в статье [338]. Они преобладают в усилении теплоемкости
для полуметаллических ферромагнетиков и могут быть важны, помимо эффектив-
ного усиления массы (G.55), для "обычных"магнетиков с хорошо локализованными
моментами.
G.2 Антиферромагнетики
Для рассмотрения электронного и магнонного спектров металлического антиферро-
магнетика в s-d(f) обменной модели перейдем к локальной системе координат со-
гласно (E.8). Тогда гамильтониан s-d(f) обменного взаимодействия примет вид
H
sd
= −I
X
kq
[S
x
q
(c
†
k+q↓
c
k↓
− c
†
k+q↑
c
k↑
) (G.68)
+iS
y
q
(c
†
k−Q↓
c
k−Q↑
− c
†
k+q↑
c
k−Q↓
)
+S
z
q
(c
†
k+q↑
c
k−Q↓
+ c
†
k−Q↓
c
k−q↑
)]
Переходя к магнонному представлению с использованием (E.1), (E.10) и вычисляя
электронную собственную энергию во втором порядке по I, получаем
Σ
k
(E) =
I
2
S
2
E − t
k−Q
(G.69)
+
1
2
I
2
S
X
q
½
(u
q
− v
q
)
2
·
1 − n
k−q
+ N
q
E − t
k−q
− ω
q
+
n
k−q
+ N
q
E − t
k−q
+ ω
q
¸
+(u
q
+ v
q
)
2
·
1 − n
k+q−Q
+ N
q
E − t
k+q−Q
− ω
q
+
n
k+q−Q
+ N
q
E − t
k+q−Q
+ ω
q
¸¾
где S - намагничeнность подрешетки. В приближении среднего поля электронный
спектр содержит две расщепленные антиферромагнитные подзоны:
E
1,2
k
=
1
2
(t
k
+ t
k−Q
) ±
1
2
[(t
k
− t
k−Q
)
2
+ 4I
2
S
2
]
1/2
(G.70)
Помимо зависимости S(T ), при вычислении температурной зависимости электрон-
ного спектра важны флуктуационные поправки (второй член в (G.68)). Рассмотрим
магнонные вкдады от функций Бозе
δE
k
(T ) = I
2
S
X
q
·
−2
u
2
q
+ v
2
q
t
k
− t
k−Q
+
(u
q
− v
q
)
2
t
k
− t
k−q
+
(u
q
+ v
q
)
2
t
k
− t
k+q−Q
¸
N
q
(G.71)
241

Поправки к энергии дна зоны (t
k
= t
min
) из-за намагниченности подрешетки (пер-
вый член в квадратных скобках) и из-за поперечных флуктуаций имеют противопо-
ложные знаки. Вклад от флуктуаций преобладает, что приводит к "синему"сдвигу
дна зоны проводимости с уменьшением температуры, который наблюдается в анти-
ферромагнитных полупроводниках [352,686], в отличие от "красного"сдвига в фер-
ромагнитных полупроводниках (ср.(G.36)). (Подобная ситуация происходит и при
высоких температурах [686,687].) В частности, в приближении ближайших соседей
для простых решеток, когда t
k+Q
= −t
k
, вклад от флуктуаций больше по абсолют-
ному значению в два раза. Интегрирование дает (z - число ближайших соседей)
δE
min
(T ) = −
3
16
I
2
S
W
³
z
2
´
3/2
(S + 1)
3/2
µ
T
T
N
¶
2
(G.72)
T
2
-зависимость электронного спектра (такая же, как и у намагниченности подрешет-
ки) является следствием линейной дисперсии спектра спиновой волны и зависимо-
сти амплитуды электрон-магнонного взаимодействия вида q
−1
, которые специфичны
для антиферромагнетиков. Поведение электронного спектра в ферримагнетике ка-
чественно подобно поведению в ферромагнетиках (зависимость T
5/2
) [687].
Запишем также многоэлектронный вклад третьего порядка к сорбственной, ко-
торый описывает перенормировку антиферромагнитной щели из-за подобных рас-
ходимостей кондовского типа [367] (см. Главу 6)
δΣ
(3)
k
(E) = 2I
3
S
2
X
q
n
k+q
(E − t
k+q
)
1
(E − t
k+q
)
2
− ω
2
q
(G.73)
×
µ
1
t
k+q
− t
k−Q+q
−
1
E − t
k+Q
¶
Для исследования магнонного спектра вычислим запаздывающую коммутатор-
ную функцию Грина
Γ
q
(ω) = hhb
q
|b
†
q
ii
ω
,
¯
Γ
q
(ω) = hhb
†
−q
|b
†
q
ii
ω
Записывая цепочку уравнений движения до второго порядка по I и выполняя про-
стейшее возможное расцепление, получаем [716] (ср. (E.9))
Γ
q
(ω) =
ω + C
q−ω
(ω − C
qω
)(ω + C
q−ω
) + D
2
qω
(G.74)
¯
Γ
q
(ω) =
D
qω
(ω − C
qω
)(ω + C
q−ω
) + D
2
qω
(G.75)
C
qω
= S(J
tot
Q+q,ω
+ J
tot
qω
− 2J
tot
Q0
) +
X
p
[C
p
Φ
pqω
−(C
p
− D
p
)Φ
p00
+ φ
+
pqω
+ φ
−
pqω
] + g
q
(G.76)
D
qω
= D
q−ω
= S(J
tot
qω
− J
tot
Q+q,ω
) +
X
p
D
p
Φ
pqω
+ h
q
242

где s-d обменные вклады первого порядка по 1/2S соответствуют приближению РК-
КИ
J
tot
qω
= J
q
+ J
RKKY
q
(ω) = J
q
+ I
2
X
k
n
k
− n
k−q
ω + t
k
− t
k−q
(G.77)
J
RKKY
q
(ω) есть зависящая от ω Фурье-компонента интеграла косвенного обменно-
го взаимодействия через электроны проводимости (ср. (K.1)). Функция Φ, которая
определяет поправки второго порядка, имеет вид
Φ
pqω
= (φ
+
pqω
− φ
−
pqω
)/ω
p
(G.78)
φ
±
pqω
= I
2
X
k
n
k
(1 − n
k+p−q
) + N
B
(±ω
p
)(n
k
− n
k+p−q
)
ω + t
k
− t
k+p−q
∓ ω
p
ω
p
- магнонная частота нулевого порядка по I и 1/2S. В (G.76) были приняты во
внимание уравнения типа
(ω − t
k
+ t
k+q
)hhc
†
k+q↑
c
k↑
|b
†
q
ii
ω
= I
µ
S
2
¶
1/2
(n
k+q
− n
k
)hhb
q
|b
†
q
ii
ω
(G.79)
и выражения для статических корреляционных функций, появляющихся в уравне-
ниях движения
I
X
k
hc
†
k−Q↓
c
k↑
i = −S(J
tot
Q0
− J
Q
) (G.80)
I
X
k
hb
†
p
(c
†
k−p↑
c
k↑
− c
†
k−p↓
c
k↓
)i = −(2S)
1/2
(C
p
− D
p
)Φ
p00
(G.81)
Они получаются при вычислении соответствующей запаздывающей функции Грина
и использовании спектрального представления (E.8). Функции
g
q
=
X
p
[(2J
Q
+ 2J
q−p
− 2J
p
− J
Q+q
− J
q
)hb
†
p
b
p
i − 2J
p
hb
−p
b
p
i] (G.82)
h
q
=
X
p
[(J
Q+q
− J
q
)hb
†
p
b
p
i − 2J
q−p
hb
−p
b
p
i]
описывают "прямое"магнон-магнонное взаимодействие. s-d обменные вклады в сред-
ние в (G.82) получаются при использовании (G.74), (G.75) в первом порядке по 1/2S
и спектрального представления
½
hb
†
q
b
q
i
hb
†
q
b
†
−q
i
¾
= −
1
π
Z
∞
−∞
dωN
B
(ω) Im
½
Γ
q
(ω)
¯
Γ
q
(ω)
¾
(G.83)
Энергетические знаменатели в (G.77), (G.78) не учитывают расщепление зоны,
которое проявляется при АФМ упорядочении. В то же самое время, важно раз-
делить вклады от переходов внутри и между АФМ подзонами. Такое разделение
может быть выполнено при учете АФМ расщепления ∆ = 2|I|S (S - намагничен-
ность подрешетки) в приближении нулевого порядка, например в рамках теории
возмущений по 1/2S. Однако соответствующие выражения очень громоздки (см. ко-
нец этого Приложения). Поэтому здесь мы используем простую теорию возмущений
243

по I, принимая во внимание, что переходы между АФМ подзонами соответствуют
передаче квазиимпульса электронов q ∼ Q. Вообще говоря, междзонные вклады в
спектральные характеристики и термодинамические свойства более сингулярны, но
фактически эти расходимости должны быть обрезаны из-за АФМ расщепления. Со-
ответствующее пороговое значение передачи магнонного квазиимпульса оценивается
как
min |q − Q| = q
0
= ∆/v
F
(v
F
- электронная скорость на уровне Ферми). Эта величина определяет характерный
температурный и энергетический масштаб
T
∗
= ω(q
0
) = cq
0
∼ (∆/v
F
)T
N
(G.84)
где c - магнонная скорость, а магнонный спектр дается полюсом (G.74),
ω
2
q
= Ω
2
q
(ω
q
) = C
2
q
(ω
q
) − D
2
q
(ω
q
)
Зависимость J
RKKY
q
(ω), которая теряется при использовании стандартного мето-
да канонического преобразования [265], является важной при вычислении магнон-
ного затухания. Затухание спиновой волны вследствие одномагнонных процессов
распада, которое определяется мнимой частью (G.77), при малых q имеет вид
γ
(1)
q
= πS[
A
L
ω
q
+ Bψ(q)] (G.85)
где L = 2S(J
0
−J
Q
), функция ψ описывает вхождение в "стонеровский континуум",
ψ(q < q
0
) = 0, ψ(q À q
0
) = 1,
A = cI
2
lim
q→0
q
X
k
δ(t
k
)δ(t
k−q
) (G.86)
B = LI
2
X
k
δ(t
k
)δ(t
k−Q
), (G.87)
t
k
отсчитывается от уровня Ферми. Вообще говоря, A зависит от направления век-
тора q. Для изотропного электронного спектра имеем
A = cI
2
v
0
{4π
2
|k
−1
∂t
k
/∂k|
2
k=k
F
}
−1
(G.88)
где v
0
- объем кристаллической ячейки.
Можно видеть, что одномагнонное затухание (G.85) конечно при произвольно ма-
лом q (в отличие от FM случая), но становится значительно большим, когда начина-
ют работать межзонные переходы (q > q
0
). Таким образом отношение γ/ω|
q→0
имеет
величину около I
2
S/W
2
и не зависит от волнового вектора и концентрации элек-
тронов [689]. Такая же ситуация, которая аналогична случаю электрон-фононного
взаимодействия, возникает для коллективизированного антиферромагнетика [690].
Линейная зависимость затухания от волнового вектора наблюдалась, например, в
антиферромагнетике Mn
0.9
Cu
0.1
[691]. Учет процессов релаксации электронов про-
водимости, которые происходят при наличии беспорядка, приводит к изменению
q-зависимости. Вычисление в такой ситуации [689] дает γ ∼ ω
2
при малых q, что
находится в согласии с гидродинамикой.
244
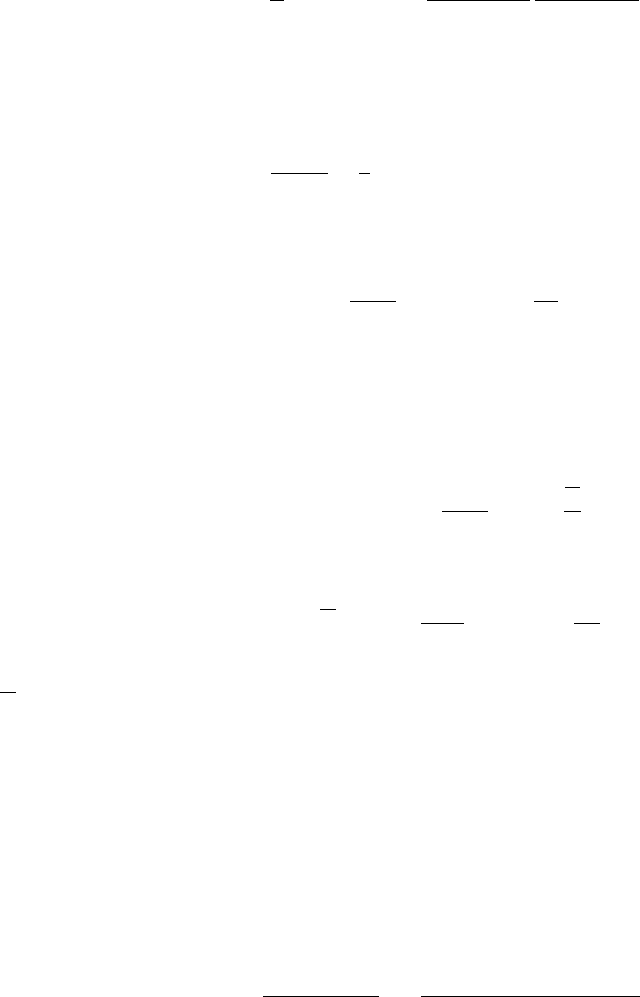
Аналогично (G.20), из (G.74), (G.77) и спектрального представления получаем
логарифмические поправки к магнонным числам заполнения и намагниченности
подрешетки (6.88), (6.89).
Затухание вследствие двухмагнонных процессов рассеяния определяется мнимой
частью функции (G.78). Оказывается, что межзонные переходы содержат меньшие
степени ω и T, но вносят вклад только при max(T, ω
q
) > T
∗
. Используя соотношение
n(²)[1 − n(²
0
)] = N(² − ²
0
)[n(²
0
) − n(²)]
и разлагая по ω = ω
q
и ω
p
, получаем из полюса (G.77)
γ
(2)
q
=
π
2
I
2
X
k,p
X
α,β=±
µ
C
q
− αD
q
ω
C
p
+ αD
p
ω
p
− β
¶
(G.89)
×(ω − βω
p
)[N
B
(ω
p
) − N
B
(ω
p
− βω)]δ(t
k
)δ(t
k+p−q
)
Интегрирование при T ¿ ω с учетом ведущих температурных поправок дает
γ
(2)
q
=
v
0
24πc
3
·
(
9
5
Aω +
˜
B)ω
2
+ 4π
2
(2Aω +
˜
B)T
2
¸
(G.90)
где
˜
B(ω À T
∗
) = B,
˜
B(ω ¿ T
∗
) = 0. При ω ¿ T получаем
γ
(2)
q
=
v
0
2πc
3
·
6ζ(3)AT +
π
2
3
˜
B
¸
T
2
(G.91)
где
˜
B(T À T
∗
) = B,
˜
B(T ¿ T
∗
) = 0, ζ(3) ' 1.2.
Неаналитические поправки к намагниченности подрешетки и магнонной частоте
появляются как от межзонных, так и от внутризонных переходов. Внутризонный
вклад в магнонную скорость имеет вид [716]
(δc/c)
1
= −
v
0
3πc
3
AT
2
ln
ω
T
(G.92)
При T > T
∗
межзонный вклад в намагниченность подрешетки имеет вид
(δS
el
)
2
= −
v
0
π
2
c
3
SLBT
∗
ln
T
T
∗
(G.93)
Полученный результаты сохраняются также в модели Хаббарда. В случае малых
S магнонное затухание играет важную роль при вычислении температурных зави-
симостей магнитных и термодинамических свойств при не слишком низких темпе-
ратурах. Они определяются вкладом от спиновых флуктуаций с малыми |q − Q|,
причем, как и для ферромагнетика, магнонное затухание играет важную роль. В
отличие от (G.21), затухание при q → Q не содержит множителя |q − Q|
−1
. (Од-
нако такая зависимость может появиться в некоторой q-области при условии, что
электронный спектр приблизительно удовлетворяет условию "нестинга"t
k+Q
= −t
k
на большом участке поверхности Ферми.) Тогда можно заменить в знаменателях
функций Грина (G.74)
1
ω
2
− Ω
2
q
(ω)
→
Aω
[ω
2
− Ω
2
q
(ω)]
2
+ A
2
ω
2
(G.94)
245

что дает для слабого коллективизированного антиферромагнетика
δS ∼ −
Z
dωN
B
(ω)
X
q
Aω
ω
4
q
+ A
2
ω
2
∼ −
µ
T
E
F
¶
3/2
(G.95)
Рассмотрим теперь электронный и магнонный спектры антиферромагнетика
Хаббарда с сильными корреляциями. Появление АФМ упорядочения приводит к
расщеплению затравочной электронной зоны на две слэтеровские подзоны [44], ко-
торые описываются новыми электронными операторами [692,693]
α
†
k
= A
k
c
†
k+Q/2↑
+ B
k
c
†
k−Q/2↓
, (G.96)
β
†
k
= A
k
c
†
k−Q/2↓
− B
k
c
†
k+Q/2↑
,
A
k
, B
k
=
1
2
µ
1 ∓
τ
k
E
k
¶
, E
k
= (τ
2
k
+ U
2
S
2
)
1/2
θ
k
, τ
k
=
1
2
(t
k+Q/2
± t
k−Q/2
)
В приближении Хартри-Фока преобразование (G.96) приводит гамильтониан Хаб-
барда к диагональной форме
H =
X
k
(E
α
k
α
†
k
α
k
+ E
β
k
β
†
k
β
k
) (G.97)
где одночастичные энергии равняются
E
α,β
k
= θ
k
∓ E
k
(G.98)
Величина
S =
X
k
hc
†
k↑
c
k+Q↓
i
которая определяет АФМ расщепление, удовлетворяет самосогласованному уравне-
нию
1 =
U
2
X
k
n
kα
− n
kβ
(τ
2
k
+ U
2
S
2
)
1/2
(G.99)
Если кулоновское взаимодействие достаточно сильно, вся энергетическая зона рас-
щеплена, так что щель появляются во всех направлениях. В частности, для одного
электрона на атом происходит переход металл-изолятор. При условии, что условия
"нестинга"t
k
−E
F
= E
F
−t
k+Q
выполняется для данного вектора Q, состояние изо-
лятора выгодно при произвольно малом U и щель будет экспоненциально малой
[692].
Чтобы получить спин-волновые поправки к приближению Хартри-Фока, перей-
дем к локальной системе координат для электронных операторов
d
†
kσ
=
1
√
2
(c
†
k+Q/2↑
+ σc
†
k−Q/2↓
) (G.100)
246
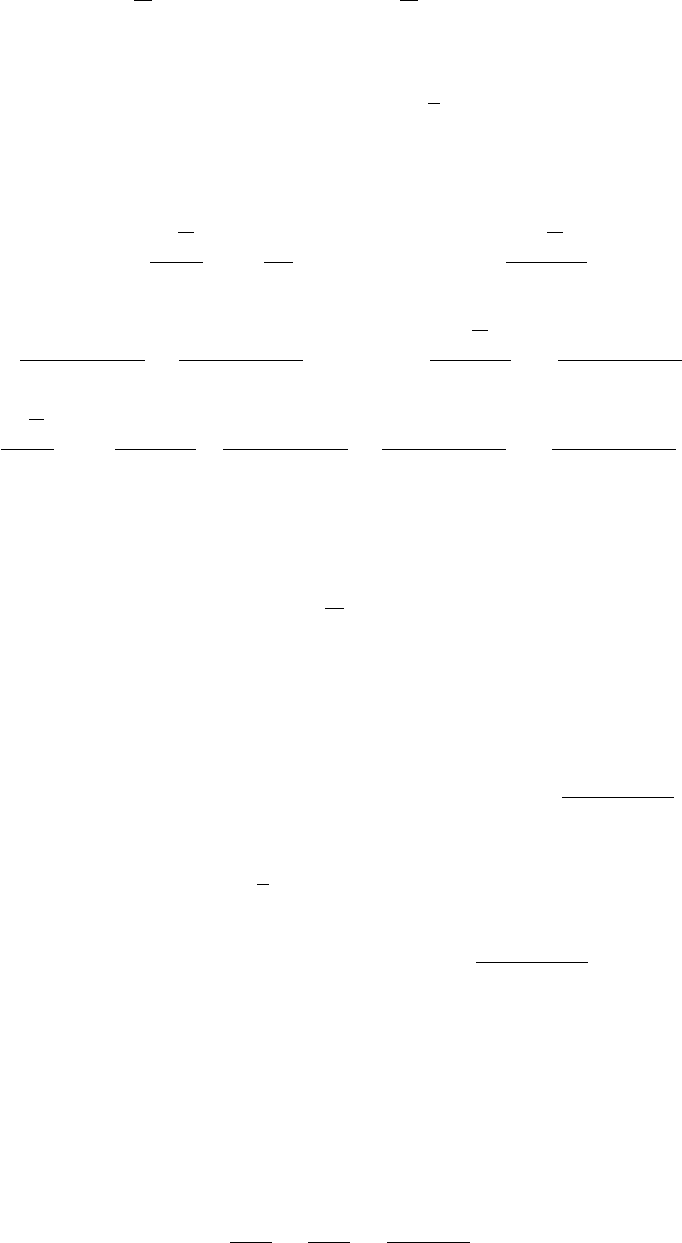
и представим гамильтониан Хаббарда в следующем виде
H =
X
kσ
[(θ
k
+
U
2
)d
†
kσ
d
kσ
+ τ
k
d
†
kσ
d
k−σ
] −
U
2
X
q
(S
−
−q
S
+
q
+ S
+
q
S
−
−q
) (G.101)
где
S
σ
q
=
X
k
d
†
kσ
d
k+q,−σ
, S
z
q
=
1
2
X
kσ
σd
†
kσ
d
k+q,σ
(G.102)
Вычисляя поперечную спиновую функцию Грина с антиферромагнитной щелью,
учитываемой в нулевом приближении, для магнонного спектра получаем [693]
ω
2
q
=
U
4
S
2
4
X
k
"
2
E
k
(n
kα
− n
kβ
) +
Ã
1 −
U
2
S
2
E
k
E
k+q
!
(G.103)
×
Ã
n
kα
− n
k+qα
E
α
k
− E
α
k+q
+
n
kβ
− n
k+qβ
E
β
k
− E
β
k+q
!
+ 2
Ã
1 +
U
2
S
2
E
k
E
k+q
!Ã
n
kα
− n
k+qβ
E
α
k
− E
β
k+q
!#
2
−
U
4
S
2
4
"
X
k
τ
k
τ
k+q
E
k
E
k+q
Ã
n
kα
− n
k+qα
E
α
k
− E
α
k+q
+
n
kβ
− n
k+qβ
E
β
k
− E
β
k+q
− 2
n
kα
− n
k+qβ
E
α
k
− E
β
k+q
!#
2
Для малого U можно разложить (G.103), что дает результат (G.74)-(G.77) с I → U.
В случае большого U и полузаполненной зоны проводимости, получаем результат
(E.12) с
J
q
= −
2
U
X
k
t
k
t
k+q
(G.104)
причем (G.94) - интеграл кинетического обмена (см. п. 5.1). Наконец, в случае U →
∞ и нецелого наполнения зоны, где носители тока приводят к негейзенберговскому
двойному обменному взаимодействию, получаем
ω
2
q
=
(
J
H
Q
− J
H
q
+
X
k
·
(Θ
k+q
− Θ
k
)n
k
+ τ
k
(τ
k+q
+ τ
k
)
n
k+q
− n
k
Θ
k+q
− Θ
k
¸
)
×
½
1
2
(J
H
Q
− J
H
Q+q
− J
H
Q−q
) (G. 105)
+
X
k
·
(Θ
k+q
− Θ
k
)n
k
− τ
k
(τ
k+q
− τ
k
)
n
k+q
− n
k
Θ
k+q
− Θ
k
¸
)
где
n
k
= n
kβ
= f(Θ
k
), n
kα
≡ 1
и взаимодействие Гейзенберга J
H
вводится для стабилизации антиферромагнитного
состояния.
Спин-волновые поправки к электронному спектру определяются, также как и
для ферромагнетика (ср. (G.13), (G.36), (G.60)), амплитудой электрон-магнонного
взаимодействия
δE
i
k
δN
q
=
δω
k
δn
ki
=
δ
2
hH
sw
i
δN
q
δn
ki
(G.106)
247

Соответствующие поправки к свободной энергии имеют вид
δF
sw
= −
1
3
δhH
sw
i = −
1
3
X
q
ω
q
N
q
∼ −
µ
T
T
N
¶
4
(G.107)
(разница с (G.60) происходит из-за линейного закона дисперсии спиновых волн).
Температурная зависимость локального момента дается теоремой Геллмана-
Фейнмана:
δhS
2
i
i = −
3
2
δN
2
= −
3
2
∂
∂U
δF
sw
∼ T
4
(G.108)
Рассматриваемое приближение типа Хартри-Фока с флуктуационными поправ-
ками дает те же результаты для электронного и магнонного спектров в случае s-d
модели (с заменой U → I). В частности, при |I| → ∞ электронный спектр со учетом
спин-волновых и многоэлектронных поправок имеет вид [693]
E
α
k
= −I(S + n
β
), E
β
k
= −I(S + 1 − n
α
)
Таким образом, обобщенное приближение Хартри-Фока дает корректные "атом-
ные"значения E = ±IS, ±I(S + 1) (Приложение I) в случае целочисленных величин
n
α
, n
β
.
248

Приложение H
Модель Хаббарда с сильными
корреляциями
Модель Хаббарда с вырожденной зоной в некоторых случаях применима к d-
электронам в переходных металлах и их соединениях. Соответствующий гамиль-
тониан имеет вид
H =
X
kmσ
t
k
a
†
klmσ
a
klmσ
+ H
int
(H.1)
где t
k
- зонная энергия. Для простоты мы не учитываем зависимость интегралов
переноса от m, т.е. пренебрегаем эффектами кристаллического поля и сохраняем в
(C.31) только вклад с λ = 0. Такое приближение позволяет в простейшем случае рас-
смотреть эффекты многоэлектронной термовой структуры в спектре.В многоэлек-
тронном представлении операторов Хаббарда (A.22) гамильтноиан взаимодействия
принимает диагональный вид
H
int
=
X
iΓ
E
Γ
X
i
(Γ, Γ) (H.2)
где энергии E
Γ
определены в (C.19) и не зависят от проекций момента. Однако
рассмотрение члена кинетической энергии становится более трудным из-за сложных
коммутационных соотношений для X-операторов (A.36).
Рассмотрим одноэлектронную функцию Грина. Согласно (A.31),
G
kγ
(E) = hha
kγ
|a
†
kγ
ii
E
=
X
nΓ
n
Γ
n−1
n
1/2
G
Γ
n
Γ
n−1
C
Γ
n
Γ
n−1
,γ
hhX
k
(Γ
n−1
, Γ
n
)|a
†
kγ
ii
E
(H.3)
В уравнении движения для функции Грина в правой части (H.3) выполним про-
стейшее расцепление, которое соответствует расцеплению на разных узлах решетки
“Хаббард-I” [28,29,31]:
(E − E
Γ
n
+ E
Γ
n−1
)hhX
k
(Γ
n−1
, Γ
n
)|a
†
kγ
ii
E
= n
1/2
G
Γ
n
Γ
n−1
C
Γ
n
Γ
n−1
,γ
(N
Γ
n
+ N
Γ
n−1
) [1 + t
k
G
kγ
(E)]
Тогда получаем
G
kγ
(E) =
Φ
γ
(E)
1 − t
k
Φ
γ
(E)
(H.4)
249

где
Φ
γ
(E) =
X
nΓ
n
Γ
n−1
n
³
G
Γ
n
Γ
n−1
C
Γ
n
Γ
n−1
,γ
´
2
N
Γ
n
+ N
Γ
n−1
E − E
Γ
n
+ E
Γ
n−1
(H.5)
Отметим, что выражения (H.4), (H.5) имеют структуру, которая напоминает
(F.8),(F.9). Как и в Приложение F, наше рассмотрение легко обобщается с учетом
одноузельного кристаллического поля (см. также [29]). Используя для E
Γ
прибли-
жение (C.20), можно просуммировать генеалогические коэффициенты в (H.5). Тогда
зависимость от МЭ квантовых чисел L, S исчезает, что соответствует приближению
[29].
В отсутствие магнитного и орбитального упорядочения числа заполнения N
Γ
в
(H.5) не зависят от проекции спина и мы имеем
Φ
Γ
(E) =
X
nΓ
n
Γ
n−1
n
2[l]
([S
n−1
][L
n−1
])
−1
(G
Γ
n
Γ
n−1
)
2
N
Γ
n
+ N
Γ
n−1
E − E
Γ
n
+ E
Γ
n−1
(H.6)
Спектр возбуждений определяется уравнением
1 − t
k
Φ
γ
(E) = 0 (H.7)
Таким образом межузельный электронный перенос ведет к размытию каждого пере-
хода между атомными уровнями в хаббардовскую подзону. Эти подзоны разделены
корреляционными щелями. В частности, для s-зоны мы получаем спектр, который
содержит в ферромагнитной фазе четыре подзоны
E
1,2
kσ
=
1
2
n
t
k
+ U ∓
£
(t
k
− U)
2
+ 4t
k
U(N
−σ
+ N
2
)
¤
1/2
o
(H.8)
Для более общей модели (C.23),
E
1,2
kσ
=
1
2
h
β
(00)
k
(N
0
+ N
σ
) + β
(22)
k
(N
2
+ N
−σ
) + U
i
∓
1
2
nh
β
(00)
k
(N
0
+ N
σ
) (H.9)
− β
(22)
k
(N
2
+ N
−σ
) − U
i
2
+ 4
¯
¯
¯
β
(02)
k
¯
¯
¯
2
(N
0
+ N
σ
)(N
2
+ N
−σ
)
¾
1/2
Выражения (H.8), (H.9) могут быть также переписаны через одноэлектронные числа
заполнения, поскольку
N
σ
+ N
2
= n
σ
, N
σ
+ N
0
= 1 − n
−σ
Можно видеть, что, в отличие от приближения Стонера (G.3), зависимость спектра
от чисел заполнения не сводится к постоянномй сдвигу подзон. Спектр Хаббард-I
имеет наиболее простой вид в случае больших U, когда
E
1
kσ
= (1 − n
−σ
)t
k
, E
2
kσ
= t
k
n
−σ
+ U (H.10)
Можно предположить, что в действительности некоторые подзоны плохо опреде-
лены из-за большого затухания. В Приложении J продемонстрировано, что в насы-
щенном ферромагнитном состоянии в приближениях высших порядков некоторые
250
