Ирхин В.Ю., Ирхин Ю.П. Электронная структура, корреляционные эффекты и физические свойства d - и f-переходных металлов и их соединений
Подождите немного. Документ загружается.

Приложение M
Аппарат матрицы плотности для
вывода кинетических уравнений и
теория аномального эффекта Холла
Математическое описание кинетических явлений связано с уравнением баланса для
функции распределения носителей тока во внешних электрических, магнитных и
тепловых полях (5.14). В простых случаях такие уравнения могут быть получе-
ны из простого физического рассмотрения движения электрона в k-пространстве
под действием внешних полей и столкновений. Однако в более сложных ситуациях,
когда важны высшие порядки по амплитуде рассеяния, такие простые аргументы
недостаточны. Так как часто мы действительно встречаемся с этой ситуацией для
кинетических явлений в магнитных кристаллах, необходим более общий метод для
вывода кинетических уравнений. Наиболее удобен подход, который использует мат-
рицу плотности. Уравнения движения для этой величины имеют обычный кванто-
вомеханический вид и могут быть легко сведены к кинетическим уравнениям.
Определим оператор матрицы плотности
bρ = e
−βH
/Spe
−βH
, β ≡ 1/T (M.1)
где H - полный гамильтониан системы, включая носители тока, рассеивающую си-
стему и внешние поля. Коэффициент в (M.1) определяется из условия нормировки
Spbρ = 1
Оператор bρ, как и H, может быть записан в любом квантовом представлении. В
теории твердого тела удобно использовать представление вторичного квантования.
Тогда символ Sp означает суммирование по всем возможным числам заполнения
квазичастиц в системе. Например, в случае электрон-фононной системы
Sp... =
X
{n
k
}{N
q
}
... (M.2)
где n
k
= 0, 1 - числа заполнения электронов, а N
q
- фононов.
Среднее значение физической величинв A получается как
hAi = Sp(bρA) (M.3)
271

Для примера вычислим средние числа заполнения для невзаимодействующих элек-
тронов проводимости. Мы находим
hn
k
i = hc
†
k
c
k
i =
X
{n
k
0
}
h...n
k
... |
Y
k
0
exp(−βε
k
0
c
†
k
0
c
k
0
)
×c
†
k
c
k
| ...n
k
...i/
X
{n
k
0
}
h...n
k
... |
Y
k
0
exp(−βε
k
0
c
†
k
0
c
k
0
) | ...n
k
...i
=
X
n
k
exp(−βε
k
)n
k
/
X
n
k
exp(−βε
k
) = (exp(βε
k
) + 1)
−1
т.е. получается функция распределения Ферми
Если гамильтониан системы записан в виде
H = H
0
+ H
0
где H’ - возмущение, равновесная матрица плотности bρ(H) может быть разложена по
степеням H’, что и требуется при вычислении полевого члена в кинетическом урав-
нении. С этой целью можно использовать теорему о разложении экспоненциального
оператора [706]:
hn|exp(−β(H
0
+ H
0
))|n
0
i = δ
nn
0
exp(−βE
0
n
)
−
exp(−βE
0
n
) − exp(−βE
0
n
)
E
0
n
− E
0
n
0
hn|H
0
|n
0
i +
X
n
00
hn|H
0
|n
00
ihn
00
|H
0
|n
0
i
E
0
n
00
− E
0
n
0
×
·
exp(−βE
0
n
0
) − exp(−βE
0
n
)
E
0
n
− E
0
n
0
−
exp(−βE
0
n
00
) − exp(−βE
0
n
)
E
0
n
− E
0
n
00
¸
(M.4)
где E
0
n
- собственные значения H
0
. В представлении вторичного квантования числа
n означают наборы чисел заполнения, и суммирование по ним дает выражение для
bρ(H) через степени H’ и bρ(H ) = bρ
0
. В представление волновых функций |l i имеем
bρ = bρ
(0)
+ bρ
(1)
+ bρ
(2)
+ ...
bρ
(0)
ll
0
= ρ
l
δ
ll
0
, bρ
(1)
ll
0
=
ρ
l
− ρ
l
0
ε
l
− ε
l
0
H
0
ll
0
(M.6a)
где
bρ
(2)
ll
0
= γρ
l
δ
ll
0
+
X
l
00
H
0
ll
00
H
0
l
00
l
0
ε
l
− ε
l
0
µ
ρ
l
− ρ
l
0
ε
l
− ε
l
0
−
ρ
l
− ρ
l
00
ε
l
− ε
l
00
¶
(M.6b)
γ =
X
ll
0
|H
0
ll
0
|
2
ε
l
− ε
l
0
·
ρ
l
− ρ
l
0
ε
l
− ε
l
0
−
∂ρ
l
∂ε
l
¸
(M.6c)
Уравнение движение для оператора матрицы плотности имеет обычный вид
∂bρ
∂t
= [H, bρ] (M.7)
В любом представление |li мы можем записать систему уравнений для диагональ-
ных и недиагональных матричных элементов. При некоторых условиях эта система
272

сводится к кинетическим уравнениям в низшем и следующем борновских приближе-
ниях. Таким путем быле получены кинетические уравнения для упругого рассеяния
на примесях [458], а затем для рассеяния фононами [460] и спиновыми неоднородно-
стями [466]. Теория в случае произвольно большой амплитуды рассеяния, но малой
концентрации примесей была развита Латтинджером [707]. Однако для сложного H
0
вычисления в матричной форме довольно громоздки даже для примесного рассея-
ния во втором борновском приближении. Поэтому для практических целей удобно
вывести кинетические уравнения в операторной форме без конкретизации гамиль-
тониана. Сейчас мы рассмотрим эту технику, развитую в [471,472].
Единственное требование к гамильтониану - возможность представления
H
t
= H
0
+ H
E
e
st
+ H
0
(M.8)
где H
0
имеет диагональный вид в n-представлении, H
E
- энергия системы в адиа-
батически включаемом (s → 0) электрическом поле E, H
0
- недиагональная часть.
Полный оператор матрицы плотности записывается как
bρ
t
= bρ + e
st
(
b
f
a
−
b
f
b
) (M.9)
где bρ - рановесная матрица плотности в отсутствие электрического поля,
b
f
a
и
b
f
b
диагональные и недиагональные компоненты поправки. Учитывая соотношения
[H
0
,
b
f
a
] = [H
0
,
b
f
a
]
a
= [H
0
,
b
f
b
]
a
мы получаем в линейном приближении по E
s
b
f
a
= [H
E
, bρ]
a
+ [H
0
,
b
f
b
]
a
(M.10)
b
f
b
=
b
L
−1
n
[H
E
, bρ]
b
+ [H
0
,
b
f
a
+
b
f
b
]
b
o
(M.11)
где
b
L
−1
=
1
is − ∆
, ∆
b
f
b
= [H
0
,
b
f
b
] (M.12)
∆ - разность собственных значения H в соответствующих состояниях. Система
(M.10), (M.11) может быть решена методом итераций. Подставляя (M.11) в (M.10),
получаем
is
b
f
b
= [H
E
, bρ]
a
+ [H
0
,
b
L
−1
n
[H
E
, bρ]
b
+ [H
0
,
b
f
a
+
b
f
b
]
b
o
]
a
(M.13)
Повторяя процедуру, имеем после n-1 итерации
is
b
f
a
= [H
E
, bρ]
a
+ [H
0
,
b
L
−1
n
[H
E
, bρ]
b
+ [H
0
,
b
f
a
]
b
+ [H
0
,
b
L
−1
n
[H
E
, bρ]
b
+ [H
0
,
b
f
a
]
b
+ [H
0
,
b
L
−1
nn
[H
E
, bρ]
b
+ [H
0
,
b
f
a
]
b
+ ...
o
(M.14)
+ [H
0
,
b
L
−1
n
...
n
[H
E
, bρ]
b
+ [H
0
,
b
f
a
+
b
f
b
]
b
o
...
ooo
]
a
где {...{ означает n фигурных скобок. Итерационная процедура позволяет получить
решение в любом нужном порядке по H
0
при условии, что разложение
b
f
a
по H
0
начинается с более низкой степени H
0
, чем разложение
b
f
b
. Тогда с точностью до
273

(H
0
)
n+1
мы можем пренебречь членом [H
0
,
b
f
b
] в (M.14), получить решение для
b
f
a
и
далее найти
b
f
b
из (M.10).
Рассмотрим первую итерацию. В низшем порядке по H
0
имеем
[H
E
, bρ
(0)
]
b
+ [H
0
,
b
L
−1
[H
0
,
b
f
a
]
b
]
a
= 0 (M.15)
Учитывая тожество
b
L
−1
nn
0
+
b
L
−1
n
0
n
= −
µ
1
∆
nn
0
+
1
∆
n
0
n
¶
− iπ[δ(∆
nn
0
) + δ(∆
n
0
n
)] (M.16)
умножая на n
λ
= a
†
λ
a
λ
и суммируя по числам заполнения, мы получаем из (M.15)
C
(0)
λ
+ T
(0)
λ
= 0 (M.17)
где
C
(0)
λ
= Sp{[H
E
, bρ
(0)
]n
λ
} (M.18)
- полевой член,
T
(0)
λ
= Sp
n
[H
0
,
b
L
−1
[H
0
,
b
f
a
]
b
]
a
n
λ
o
(M.19)
= 2πiSp{H
0
b
f
a
H
0
− H
0
H
0
b
f
a
}δ(∆)n
λ
столкновительный член (δ-функции соответствуют подчеркнутому оператору H
0
).
Легко видеть, что
b
f
a
=
b
f
(−2)
∼ (H
0
)
−2
. Таким образом мы получаем обычное кине-
тическое уравнение типа Больцмана
В приближении следующего порядка по H
0
мы должный учесть члены с
b
f
(−1)
∼
(H
0
)
−1
. Находим
C
(1)
λ
+ C
0(1)
λ
= T
(0)
λ
(f
(−1)
) + T
(0)
λ
(f
(−2)
) = 0 (M.20)
где
C
(1)
λ
= Sp{[H
E
, bρ
(1)
]n
λ
} (M.21)
C
0(1)
λ
= 2πiSp{[H
0
, bρ
(0)
H
E
− H
0
H
E
bρ
(0)
]n
λ
δ(∆)} (M.22)
и, в случае чисто мнимого произведения H
0
H
0
H
0
(например, для спин-орбитального
взаимодействия),
T
(1)
λ
= 6π
2
Sp{
b
f
a
δ(∆)H
0
n
λ
H
0
H
0
δ(∆)} (M.23)
Видно, что одно из важных преимуществ метода - простое формирование членов с
дельта-функциями.
Во втором порядке по H
0
C
(2)
λ
+ C
0(2)
λ
+ C
00(2)
λ
+ T
(0)
λ
(f
(0)
) + T
(1)
λ
(f
(−)
) + T
(2)
λ
(f
(−2)
) = 0 (M.24)
где
C
(2)
λ
= Sp{[H
E
, bρ
(2)
]n
λ
} (M.25)
C
0(2)
λ
= Sp{[H
0
,
b
L
−1
[H
E
, bρ
(1)
]]n
λ
} (M.26)
C
00(2)
λ
= Sp{[H
0
,
b
L
−1
[H
0
,
b
L
−1
[H
E
, bρ
(0)
]]]n
λ
} (M.27)
T
(2)
λ
= Sp{[H
0
,
b
L
−1
[H
0
,
b
f
a
]
b
[[H
0
, bn
λ
]
b
L
−1
, H
0
]
b
b
L
−1
} (M.28)
В матричной форме этот результат был выведен Коном и Латтинджером [478]. Далее
мы рассматриваем кинетические уравнения для конкретных механизмов рассеяния.
274

M.1 Примесное рассеяние
Гамильтноиан электронно-примесной системы имеет вид
H
0
=
X
l
ε
l
c
†
l
c
l
, H
E
= eE
X
ll
0
r
ll
0
c
†
l
c
l
0
, H
0
=
X
ll
0
V
ll
0
c
†
l
c
l
0
(M.29)
где l = {nk}, n - зонный индекс,
V
ll
0
=
n
i
X
i=1
e
i(k−k
0
)R
i
ϕ
ll
0
(M.30)
ϕ
ll
0
=
Z
dre
i(k−k
0
)r
u
∗
l
(r)u
l
0
(r)ϕ(r) (M.31)
ϕ(r) - однопримесный потенциал, n
i
- число примесей, u
l
- блоховские множители в
(2.1). Усреднение по случайному распределению примесей дает
h|V
ll
0
|
2
i = n
i
|ϕ
ll
0
|
2
(l 6= l
0
) (M.32)
Диагональные матричные элементы примесного потенциала могут быть включены в
нулевой гамильтониан и не важны при выводе кинетического уравнения. Рассмотрим
уравение низшего порядка (M.17). Подставляя H
E
и H
0
в (M.18), (M.19), получаем
C
(0)
l
= eE
α
X
l
0
(ρ
(0)
ll
0
r
α
l
0
l
− r
α
ll
0
ρ
(0)
l
0
l
) = eE[bρ
(0)
, r]
l
= ieE
∂n
l
∂k
(M.33)
(здесь и далее мы используем обозначение n
l
= ρ
(0)
l
= f(ε
l
) для равновесной ферми-
евской функции распределения),
T
(0)
l
= 2πi
X
l
0
|ϕ
ll
0
|
2
(f
l
0
− f
l
)δ(ε
l
0
− ε
l
) (M.34)
где
f
l
= Sp(
b
f
a
c
†
l
c
l
) (M.35)
Выражения (M.33), (M.34) дают полевой и столкновительный члены кинетического
уравнения для упругого рассеяния примесями в борновском приближении. Результа-
ты в двух следующих порядках были получены Латтинджером [459]. Кинетическое
уравнение второго борновском приближения для примесного рассеяния имеет вид
(поправки первого порядка к полевому члену отсутствуют)
T
(1)
l
(f
(−2)
) + T
(0)
l
(f
(−1)
) = 0 (M.36)
где
T
(1)
l
= −2π
X
l
0
l
00
δ(ε
l
− ε
l
0
)[(L
(−1)
)
ll
00
hV
ll
00
V
l
00
l
0
V
l
0
l
i
+(L
(−1)
)
∗
ll
00
hV
ll
0
V
l
0
l
00
V
l
00
l
i(f
l
− f
l
0
)] (M.37)
и T
(0)
l
определяется (M.34).
275
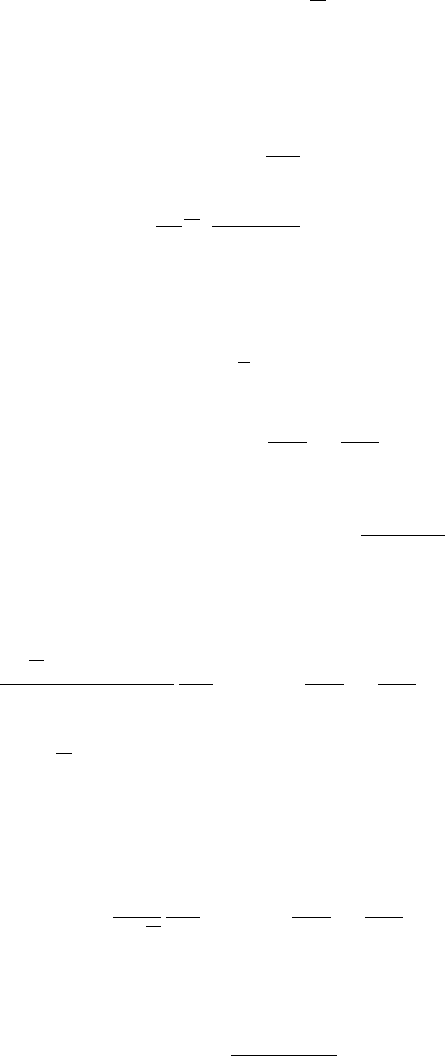
Рассмотрим случай, когда присутствует спин-орбитальное взаимодействие
(СОВ). Выделяя в (M.37) мнимую часть, линейную по СОВ, и усредняя по при-
месям, получаем
T
(2)
l
(f
(−2)
) = −(2π)
2
n
i
X
l
0
l
00
δ(ε
l
− ε
l
0
)δ(ε
l
− ε
l
00
)(f
(−2)
l
− f
(−2)
l
0
) Im(ϕ
ll
0
ϕ
l
0
l
00
ϕ
l
00
l
) (M.38)
Предполагая что эффективный радиус r
0
потенциала ϕ(r) мал (k
F
r
0
¿ 1), мы можем
положить
ϕ
kk
0
≈
Z
drϕ(r) = ϕ (M.39)
Тогда, используя приближение эффективной массы, мы получаем решение в первом
борновском приближении (благодаря дельта-функциям нужно учитывать только вн-
туризонные переходы)
f
(−2)
l
= −τ
0
eE
∂n
l
∂ε
l
v
l
(M.40)
τ
−1
0
=
n
i
2π
ϕ
2
(2m∗)
3/2
¯h
4
E
1/2
F
(M.41)
Для вычисления поправок от СОВ мы должны разложить матричные элементы
(M.31) по малым |k − k
0
|:
Im(ϕ
ll
0
ϕ
l
0
l
00
ϕ
l
00
l
) =
i
2
ϕ
kk
0
ϕ
k
0
k
00
ϕ
k
00
k
×(k
0
α
− k
00
α
)(k
0
β
− k
β
)
Ã
∂J
l
α
∂k
β
−
∂J
l
β
∂k
α
!
(M.42)
где
J
l
α
= J
nn
α
(k), J
nn
0
α
=
Z
dru
∗
nk
(r)
∂u
n
0
k
(r)
∂k
α
(M.43)
пропорционально СОВ и является чисто мнимым.
Подставляя (M.40), (M.42) в (M.38), находим
in
i
ϕ
3
E
2
F
τ
0
(2m
∗
)
3
12π¯h
7
∂n
l
∂ε
l
eE
α
k
β
Ã
∂J
l
α
∂k
β
−
∂J
l
β
∂k
α
!
+2πn
i
ϕ
2
X
k
δ(ε
nk
− ε
nk
0
)(f
(−1)
nk
− f
(−1)
nk
0
) = 0 (M.44)
Это уравнение имеет структуру обычного борновского уравнения с мдифицирован-
ным полевым членом. Его решение имеет вид
f
(−1)
l
= −
iE
F
3n
i
ϕ
∂n
l
∂ε
l
eE
α
k
β
Ã
∂J
l
α
∂k
β
−
∂J
l
β
∂k
α
!
(M.45)
Теперь мы оценим величины J. В первом порядке теории возмущений по СОВ по-
лучаем
u
nk
= u
(0)
nk
+
X
n
0
6=n
hn
0
|H
S0
|ni
ε
nk
− ε
nk
0
u
n
0
k
(M.46)
276

J
l
α
= −2i
X
n
0
6=n
r
α
nn
0
hn
0
|H
S0
|ni
ε
nk
− ε
nk
0
(M.47)
где матричные элементы координаты связаны с матричными элементами квазиим-
пульса
r
α
nn
0
(k) =
−iP
α
nn
0
(k)
m
∗
(ε
nk
− ε
nk
0
)
(M.48)
Полагая для простоты ε
nk
− ε
n
0
k
= ∆ = const и подставляя выражение для H
so
мы
находим
J
l
α
=
1
m
∗
∆
2
X
n
0
6=n
((H
S0
)
nn
0
P
α
n
0
n
− P
α
nn
0
(H
S0
)
n
0
n
)
=
¯h
m
∗
∆
2
[H
so,
p
α
]
n
0
n
(M.49)
Используя уравнение Пуассона
∆V (r) = −4πe
2
ρ(r) (M.50)
(ρ(r) - зарядовая плотность) и (L.1), получаем
J
l
α
= −i
2π¯h
4
e
2
ρ
eff
3m
2
c
2
m
∗
∆
2
M(0)
[kM]
α
(M.51)
где M - намагниченность,
ρ
eff
=
Z
dr|u
nk
(r)|
2
ρ(r) (M.52)
Подставляя (M.51) в (M.45) находим холловскую проводимость
σ
yx
=
ev
y
a
3
0
E
x
=
e
a
3
0
E
x
X
l
v
l
y
f
(−1)
l
(M.53)
= t
e
2
n
m
∗
2π
3∆
2
µ
2
B
¯hρ
eff
M
M(0)
E
F
3n
i
ϕ
где t - число зон, n = k
3
F
/6π
2
- концентрация электронов. Прнимая во внимание
выражение для диагональной компоненты тензора проводимости
σ
xx
=
ev
x
a
3
0
E
x
=
e
a
3
0
E
x
X
l
v
l
x
f
(−2)
l
= −τ
0
e
2
X
l
(v
l
)
2
∂n
l
∂ε
l
= t
e
2
nτ
0
m
∗
(M.54)
мы получаем для коэффициента Холла результат (5.124).
277

M.2 Рассеяние фононами
В случае электрон-фононного взаимодействия мы имеем
H
0
=
X
l
ε
l
c
†
l
c
l
+
X
q
ω
q
b
†
q
b
q
(M.55)
H
0
=
X
ll
0
q
(Q
ll
0
q
c
†
l
c
l
0
b
q
+ Q
∗
ll
0
q
c
†
l
0
c
l
b
†
q
) (M.56)
где
Q
ll
0
q
=
2
3
i(2Mω
q
)
−1/2
qC
nn
0
δ
k−k
0
,q
ω
q
частота фононов, b
†
q
и b
q
- бозевские операторы рождения и уничтожения фоно-
нов, C - константа Блоха в теории проводимости [1]. Включение второго члена в H
0
учитывает неупругий характер электрон-фононного рассеяния.
Рассмотрим приближение низшего порядка (M.17). Тогда полевой член опреде-
ляется (M.33), а член столкновений вычисляется из (M.19):
T
(0)
l
= 2πi
X
l
0
q
|Q
ll
0
q
|
2
{[(f
l
0
− f
l
)N
q
− f
l
(1 − n
l
0
) + f
l
0
n
l
0
]δ(ε
l
0
− ε
l
+ ω
q
)
+ [(f
l
0
− f
l
)(1 + N
q
) + f
l
(1 − n
l
0
) + f
l
0
n
l
0
]δ(ε
l
0
− ε
l
− ω
q
} (M.57)
Здесь мы выполнили расцепления многочастичных матриц плотности, так что N
q
и
n
nk
- равновесные бозевские и фермиевские функции.
Вклад низшего порядка в аномальный эффект Холла (АЭХ) от фононного рас-
сеяния описывается уравнением второго порядка по H’. Соответствующая поправка
к функции распределения, линейная по СОВ, возникает как от полевого, так и от
столкновительного членов. Чтобы упростить рассмотрение, мы следуем работе [460]
и не учитываем всех таких поправок, но ограничимся уравнением
C
0(2)
l
+ T
(0)
l
(f
(0)
) = 0 (M.58)
(см. (M.24)) и пренбережем C
(2)
, C
00(2)
и T
(2)
. Опущенные вкалады по-видимому не
влияют на качественные результаты.
Чтобы вычислить C
0(2)
l
, мы должны разложить равновесную функцию распре-
деления до первого порядка по амплитуде рассеяния. Выполняя расцепление мно-
гочастичных средних с использованием теоремы о разложении экспоненциальных
операторов (M.6), получаем
X
l
0
q
|Q
ll
0
q
|
2
[δ(ε
l
0
− ε
l
+ ω
q
)ϕ
(0)
ll
0
q
− δ(ε
l
0
− ε
l
− ω
q
)ϕ
(0)
ll
0
q
]
+eE
X
l
0
q
|Q
ll
0
q
|
2
βn
l
0
(1 − n
l
)(r
l
0
− r
l
)[δ(ε
l
0
− ε
l
+ ω
q
)N
q
+δ(ε
l
0
− ε
l
− ω
q
)(1 + N
q
)] = 0 (M.59)
где
ϕ
(i)
ll
0
q
= N
q
(n
l
0
− n
l
) + f
(i)
l
(1 − n
l
0
) + f
(i)
l
0
(M.60)
278
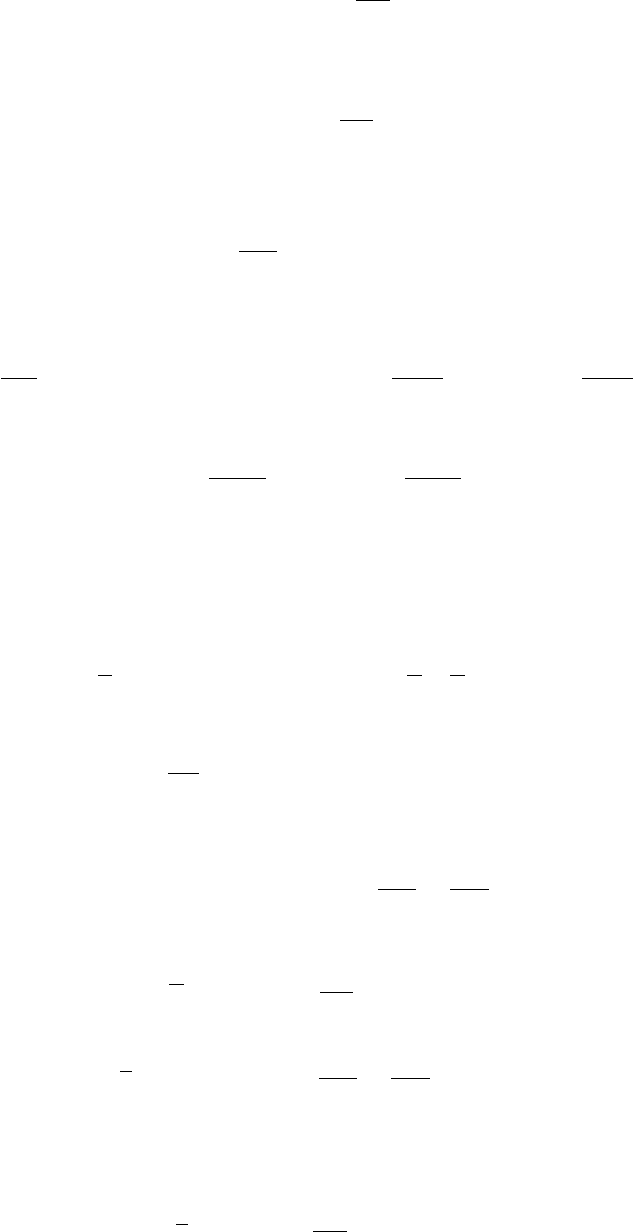
Для высоких температур T À ω
q
имеем
βn
l
0
(1 − n
l
0
) = −
∂n
l
∂ε
l
так что решение, лиенйное по СОВ, имеет вид
f
(0)
l
= ieE
α
J
l
α
∂n
l
∂ε
l
(M.61)
где величина J (см. (M.43)) определяется диагональной частью координаты, связан-
ной с СОВ [459]:
r
α
ll
0
= iδ
ll
0
∂
∂k
α
+ iJ
nn
0
α
(k)δ
kk
0
(M.62)
Недиагональная часть f
(0)
получается из уравнения (M.11):
f
(0)
l
0
l
=
1
∆
l
0
l
(
eE
α
[bρ
(0)
, r
α
]
l
0
l
−
X
l
00
q
"
Q
l
0
l
00
q
Q
ll
00
q
ϕ
(−2)
l
00
lq
∆
+
l
00
lq
− Q
∗
l
00
l
0
q
Q
l
00
lq
ϕ
(−2)
ll
00
q
∆
−
l
00
lq
− Q
ll
00
q
Q
∗
l
00
l
0
q
ϕ
(−2)
l
0
l
00
q
∆
+
l
0
l
00
q
+ Q
ll
00
q
Q
l
0
l
00
q
ϕ
(−2)
ll
00
q
∆
−
l
0
l
00
q
#)
(M.63)
где
∆
l
0
l
= ε
l
− ε
l
0
− is, ∆
±
l
0
lq
= ε
l
− ε
l
0
± ω
q
− is, s → 0
Используя (M.61) и (M.63), мы можем вычислить среднюю скорость носителей тока
в нулевом порядке по Q:
v =
X
l
f
(0)
l
v
l
+
X
l
0
6=l
f
(0)
l
0
l
v
ll
0
≡ v
a
+v
b
(M.64)
v
l
=
∂ε
l
∂k
, v
ll
0
α
= −(ε
l
− ε
l
0
)J
nn
0
α
δ
kk
0
(M.65)
Учитывая (M.62) и соотношение
X
n
0
³
J
nn
0
β
J
n
0
n
α
− J
nn
0
α
J
n
0
n
β
´
=
∂J
l
β
∂k
α
−
∂J
l
α
∂k
β
(M.66)
получаем
v
a
= ieE
α
X
l
∂n
l
∂ε
l
v
l
J
l
α
(M.67)
v
bβ
= ieE
α
X
l
n
l
Ã
∂J
l
β
∂k
α
−
∂J
l
α
∂k
β
!
(M.68)
где мы пренебрегли межзонными переходами. Интегрируя (M.68) по частям и объ-
единяя с (M.67), получаем окончательное выражение для средней скорости
v
α
= ieE
X
l
∂n
l
∂ε
l
v
l
J
l
α
(M.69)
279
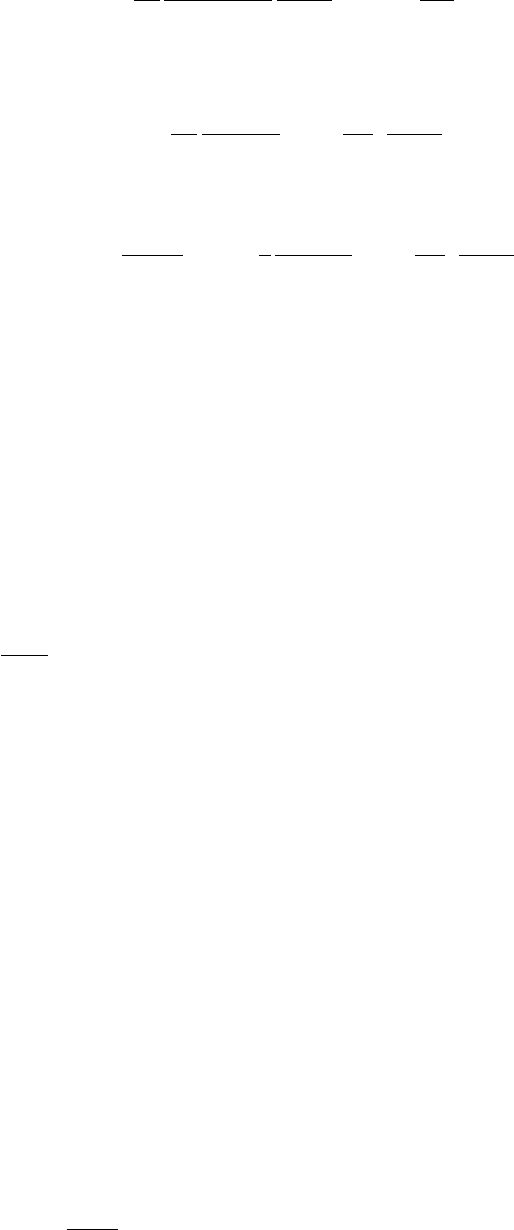
Подставляя выражение (M.51) в (M.69), получаем
σ
ph
yx
= −
2π
3
e
4
¯h
4
m
∗
(mc∆)
2
M
z
M(0)
ρ
eff
X
l
∂n
l
∂ε
l
v
l
x
k
x
(M.70)
Интегрируя по k и усредняя по подзонам, еаходим аналогично (M.53)
σ
ph
yx
=
2π
3
e
4
n¯h
4
(mc∆)
2
tρ
eff
h
1
m
∗
i
M
z
M(0)
(M.71)
Тогда спонтанный коэффициент Холла равен
R
ph
S
= −
σ
yx
4πM
z
ρ
2
= −
2
3
µ
2
B
e
2
n¯h
∆
2
ρ
eff
th
1
m
∗
i
ρ
2
M(0)
(M.72)
M.3 Рассеяние спиновыми неоднородностями
Для описания взаимодействия электронов проводимости с магнитными моментами
мы используем s-d обменную модель с включением спин-орбитального взаимодей-
ствия (L.17). В случае высоких температур введем в гамильтониан взаимодействие
электронов со средним полем:
H
d
= −W
M
X
i
S
z
i
, W
M
= 2J
0
hS
z
i (M.73)
В низшем борновском приближении находим
−eE
α
∂n
l±
∂k
α
= 2π
X
l
0
n
|I
ll
0
± Λ
z
ll
0
|
2
(f
(−2)
l
0
±
− f
(−2)
l±
)K
zz
δ(ε
l±
− ε
l
0
±
)+
+|I
ll
0
|
2
(Φ
(−2)
l±,l
0
±
K
±∓
− Φ
(−2)
l
0
±l±
K
∓±
)δ(ε
l±
− ε
l
0
±
± W
M
)+
Λ
+
l
0
l
Λ
−
l
0
l
h
(Φ
(−2)
l±,l
0
±
K
+−
− Φ
(−2)
l
0
±l±
K
−+
)δ(ε
l±
− ε
l
0
±
+ W
M
)
+ (Φ
(−2)
l±,l
0
±
K
−+
− Φ
(−2)
l
0
±l±
K
+−
)δ(ε
l±
− ε
l
0
±
− W
M
)
io
(M.74)
где
Φ
(i)
λ
0
λ
= f
(i)
λ
(1 − n
λ
0
) − f
(i)
λ
0
n
λ
(M.75)
ε
l±
= ε
l
± I
ll
hS
z
i
и мы ввели одноузельные средние
K
zz
= h(S
z
)
2
i − hS
z
i
2
, K
±∓
= hS
±
S
∓
i = h(S ± S
z
)(S ∓ S
z
+ 1)i (M.76)
пренебрегая межузельными спиновыми корреляторами в духе приближения сред-
него поля. Уравнение (M.74) было впервые получено в [466] матричным методом.
Опуская спин-орбитальные члены мы получаем в однозонном приближении (l = k)
для I
kk
0
= const результат Касуя [422]
−eE
α
∂n
k±
∂k
α
= 2πI
2
X
k
0
[(f
k
0
±
− f
k±
)K
zz
δ(ε
k±
− ε
k
0
±
) (M.77)
280
