Ирхин В.Ю., Ирхин Ю.П. Электронная структура, корреляционные эффекты и физические свойства d - и f-переходных металлов и их соединений
Подождите немного. Документ загружается.


где множитель (2[l] + 1 − n)/n - отношение статистических весов конфигураций d
n
и d
n−1
:
2[l] + 1 − n
n
=
(2[l])!
n!(2[l] − n )!
/
(2[l])!
(n − 1)!(2[l] − n + 1)!
Результат (N.26) отличается от результата теории возмущений при высоких темпе-
ратурах (6.22) только единицей в знаменателе показателя степени. Такая разница
типична для вычисления температуры Кондо в вырожденной модели Андерсона
[565,574] и объясняется тем, что этот подход оправдан, строго говоря, только в пре-
деле больших N.
291
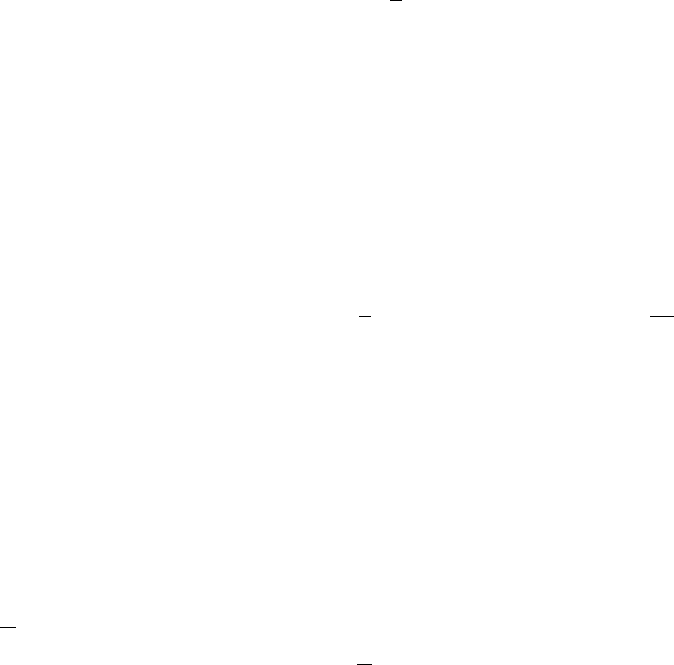
Приложение O
Приближение среднего поля для
основного состояния магнитных
решеток Кондо
Чтобы построить приближение среднего поля, описывающее основное состояние ре-
шеток Кондо, мы используем представление псевдофермионов Абрикосова для ло-
кализованных спинов S = 1/2 (которое совпадает с представлением Дирака (B.1))
S
i
=
1
2
X
σσ
0
f
†
iσ
σ
σσ
0
f
iσ
0
(O.1)
с вспомогательными условиями
f
†
i↑
f
i↑
+ f
†
i↓
f
i↓
= 1
Используя приближение перевальной точки для интеграла по траекториям, опи-
сывающего спин-фермионную взаимодействующую систему [711], можно свести га-
мильтониан s − f обменного взаимодействия к эффективной гибридизационной мо-
дели:
−I
X
σσ
0
c
†
iσ
c
iσ
µ
σ
σσ
0
S
i
−
1
2
δ
σσ
0
¶
→ f
†
i
V
i
c
i
+ c
†
i
V
†
i
f
i
−
1
2I
Sp(V
i
V
†
i
) (O.2)
где использованы векторные обозначения
f
†
i
= (f
†
i↑
, f
†
i↓
), c
†
i
= (c
†
i↑
, c
†
i↓
)
V - эффективная матрица гибридизации, определяемая из услови минимума сво-
бодной энергии. Коулмен и Андрей [711] рассмотрели формирование состояния спи-
новой жидкости в двумерной ситуации. Здесь мы исследуем более простой случай
ферромагнитного упорядочения, следуя [608]. Рассмотрим гейзенберговский гамиль-
тониан f-подсистемы в приближении среднего поля. Дл ферромагнетика мы имеем
(S = hS
z
i)
H
f
= −J
0
S
X
iσ
σf
†
iσ
f
iσ
, V
σσ
0
= V
σ
δ
σσ
0
(O.3)
292
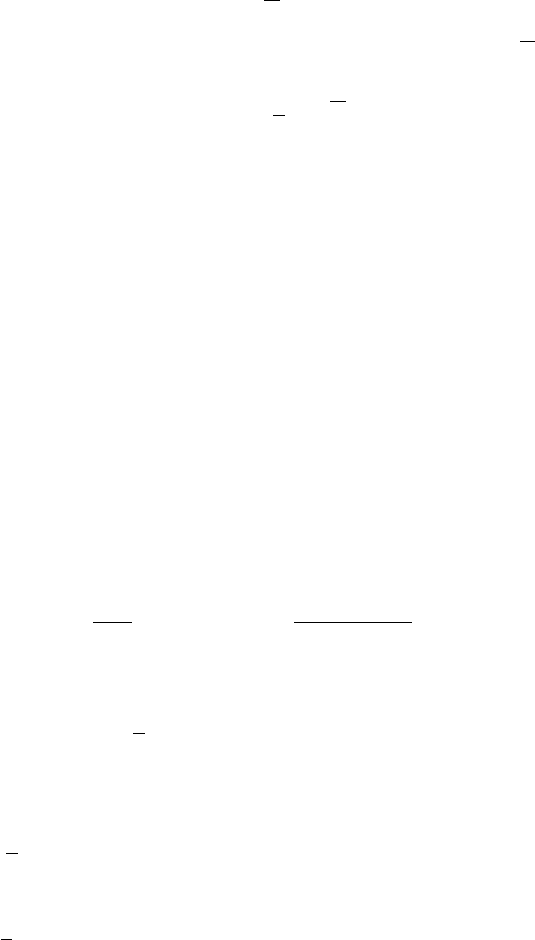
и гамильтониан s − f модели принимает вид
H − ζn =
X
kσ
[(t
k
− ζ)c
†
kσ
c
kσ
+ w
σ
f
†
kσ
f
kσ
(O.4)
+V
σ
(c
†
kσ
f
kσ
+ f
†
kσ
c
kσ
) + const
где
w
σ
= w − σJ
0
S,
w - энергия “f -уровня”. Уровнения для w, химического потенциала ζ и S имеют вид
n
†
σ
≡
X
k
hf
†
kσ
f
kσ
i =
1
2
+ σS (O.5)
n =
X
k
hc
†
kσ
c
kσ
i (O.6)
Легко видеть, что −w играет роль химического потенциала для псевдофермионов
(заметим, что числа электронов и псевдофермионов сохраняются по отдельности).
После минимизации получаем уравнение для V
σ
V
σ
= 2I
X
k
hf
†
kσ
c
kσ
i (O.7)
Диагонализуя гамильтониан (O.4) каноническим преобразованием
c
†
kσ
= u
kσ
α
†
kσ
− v
kσ
β
†
kσ
, f
†
kσ
= u
kσ
β
†
kσ
− v
kσ
α
†
kσ
(O.8)
u
kσ
= cos(θ
kσ
/2), v
kσ
= sin(θ
kσ
/2)
где
sin θ
kσ
=
2V
σ
E
kσ
, cos θ
kσ
=
t
k
− ζ − w
σ
E
kσ
(O.9)
мы получаем энергетический спектр гибридизационного типа
E
α,β
kσ
=
1
2
(t
k
− ζ + w
σ
± E
kσ
) (O.10)
И уравнения (O.5)-(O.7) принимают вид
n
f
σ
=
1
2
X
k
h
(1 − cos Θ
kσ
) n
α
kσ
+ (1 + cos Θ
kσ
) n
β
kσ
i
(O.11)
n =
1
2
X
kσ
h
(1 + cos Θ
kσ
) n
α
kσ
+ (1 − cos Θ
kσ
) n
β
kσ
i
(O.12)
1 = −2I
X
k
³
n
β
kσ
− n
α
kσ
´.
E
kσ
(O.13)
При малых |V
σ
|, |w
σ
| и T = 0 имеем
cos Θ
kσ
≈ sign (t
k
− ζ − ω
σ
) (O.14)
293
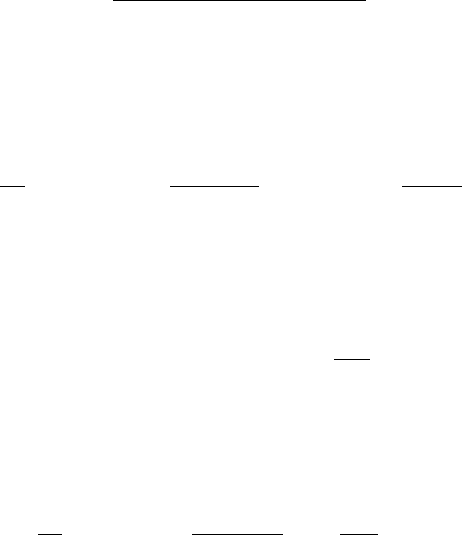
так что уравнения (O.11), (O.12) упрощаются. Края гибридизационных щелей спи-
новых подзон даются формулой
E
α
kσ
> w
σ
+ V
2
σ
/ζ, E
β
kσ
< w
σ
− V
2
σ
/(W − ζ) (O.15)
Далее мы рассмотрим различные типы ферромагнитных решений. Мы ограничимся
случаем, когда концентрация электронов проводимости n < 1 (результаты для n > 1
получаются после частично-дырочного преобразования). Как следует из (O.15), при
не слишком больших
¯
S для обеих σ выполняется условие
w
σ
> V
2
σ
/(W − ζ) (O.16)
т.е. химический потенциал лежит ниже энергетической щели, как и в немагнитном
случае. Определим функцию ζ(c) формулой
c = 2
ζ(c)
Z
0
dEρ(E) (O.17)
где ρ(E) (0 < E < W ) - затравочная плотность состояний. Тогда уравнение (O.12)
принимает вид ζ(n) = ζ, а (O.11) и (O.13) дают
λ
σ
≡ V
2
σ
/ω
σ
= ζ(n + 2n
f
σ
) − ζ(n) (O.18)
1 = −2I
ζ+λ
σ
Z
0
dEρ(E)
[(E − ζ − w
σ
)
2
+ 4V
2
σ
]
1/2
(O.19)
Вычисляя интеграл в (O.19) с точностью до ведущего и следующего порядка по
1/ ln |W/V
σ
|, мы получаем
1 = −4Iρ ln
¯
¯
¯
¯
C
V
σ
¯
¯
¯
¯
− 2I
ζ
Z
C
dE
ρ(E + ζ)
E
+
ζ(n+2n
f
σ
)
Z
C+ζ
dE
ρ(E)
E − ζ
(O.20)
где C - параметр обрезания, не входящий в окончательный результат. В ведущем
приближении V
σ
не зависит от σ и мы имеем
|V
σ
| ∼ (W T
K
)
1/2
, T
K
≡ W exp
1
2Iρ
(O.21)
Сохраняя члены следующего порядка, мы получаем самосогласованное уравнение
для намагниченности
tanh
1
4ρ
ζ(n+1+2
¯
S)
Z
ζ(n+1−2
¯
S)
dE
ρ(E) − ρ
E − ζ
=
J
0
¯
S
w
(O.22)
где
ω ≈ V
2
/[ζ(n + 1) − ζ] ∼ T
K
(O.23)
294
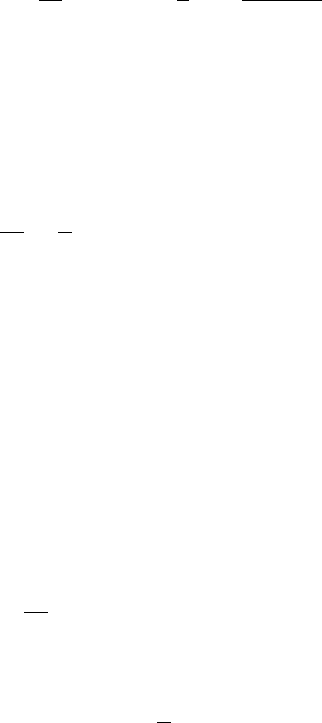
Уравнение (O.22) не имеет тривиальных решений для затравочной плотности состо-
яний ρ(E) = const. Однако решения с
¯
S 6= 0 могут возникать для некоторых ρ(E),
если левая и правая части порядка единицы, т.е. J
0
∼ T
K
(см. Рис. О.1).
При условии
w
↓
> V
2
↓
/(W − ζ), w
↑
< −V
2
↑
/ζ (O.24)
т.е. ζ лежит в энергетической щели для σ =↑, мы получаем “полуметаллическое”
ферромагнитное решение с
n
f
↑
= 1 − n/2, n
f
↓
= n/2,
¯
S = (1 − n)/2 (O.25)
(см. рис. O.2). Такое решение существует при условии
−ϕ/ζ < [ζ(2n) − ζ]
−1
− J
0
(1 − n)/V
2
↓
< ϕ/(W − ζ) (O.26)
ϕ ≡
¯
¯
¯
¯
V
↑
V
↓
¯
¯
¯
¯
2
= exp
1
ρ
W
Z
ζ(2n)
dEρ(E)
E − ζ
(O.27)
Для ρ(E) = const (O.26) принимает вид
J
0
(1 − n) < T
K
(O.28)
и соответствующая полная энергия
E =
n
2
4ρ
−
n
2
T
K
− J
0
¯
S
2
= E
non−mag
− J
0
¯
S
2
(O.29)
всегда ниже, чем немагнитное состояние Кондо. Таким образом, энергетически вы-
годно образование состояния полуметаллического ферромагнетика. В этом состо-
янии каждый электрон проводимости компенсирует один локализованный спин и
магнитный порядок обусловлен обменным взаимодействием между нескомпенсиро-
ванными моментами. Такая картина напоминает ситуацию в хаббардовской или s−d
обменной модели с узкими зонами и большим внутриузельным взаимодействием
(Разд. 4.6). В нашем случае затравочное взаимодействие мало, но эффективное вза-
имодействие велико в режиме сильной связи.
Выражение (O.29) следует сравнить с энергией обычного ферромагнитного со-
стояния с подавленным эффектом Кондо
E =
n
2
4ρ
− J
0
/4 (V
σ
= 0,
¯
S = 1/2) (O.30)
Мы видим, что последнее состояние становится энергетически выгодным при
J
0
(1 −
n
2
) > T
K
(O.31)
В критической точке происходит переход первого рода.
Третий тип возможных ферромагнитных решений соответствует ситуации боль-
шому значению расщепления, когда ζ лежит в нижней гибридизационной подзоне
для σ =↓ и в верхней дл σ =↓ (см. рис. O.3). Впрочем, такие решения (по крайней
мере для ρ(E) = const) энергетически невыгодны [608].
295

Приложение P
Представления Швингера и
Дайсона-Малеева в теории
двумерных гейзенберговских
антиферромагнетиков
Представление швингеровских бозонов имеет вид, напоминающий представление Аб-
рикосова (O.1), однако фермиевские операторы заменяются на бозевские b
iσ
:
S
i
=
1
2
X
σσ
0
b
†
iσ
σ
σσ
0
b
iσ
0
S
+
i
= b
†
i↑
b
i↓
, S
−
i
= b
†
i↓
b
i↑
, S
z
i
=
1
2
³
b
†
i↑
b
i↑
− b
†
i↓
b
i↓
´
(P.1)
При фиксированной величине локализованных спинов S эти операторы должны
удовлетворять на каждом узле i дополнительному условию
X
σ
b
†
iσ
b
iσ
= 2S (P.2)
Необходимо отметить что "гиперболические"операторы (B.14) которые изменяют
значение момента, также могут быть выражены через швингеровские бозоны [656]:
K
+
= b
†
↑
b
†
↓
, K
−
= b
↓
b
↑
, K
z
=
1
2
³
b
†
↑
b
↑
+ b
†
↓
b
i↓
+ 1
´
(P.3)
Представление (P.1) оказывается удобным при рассмотрения низкоразмерных си-
стем, которые не могут иметь дальнего порядка при конечных температурах, но
демонстрируют протяженные спиновые флуктуации (ближний порядок).
Рассмотрим теорию среднего поля для двумерной модели Гейзенберга в рам-
ках самосогласованной спин-волновой теории [623] (Она существенно отличается от
обычной теории среднего поля Разд. 4.1, поскольку позволяет описывать сильный
ближний порядок выше точки упорядочения.) Условие (P.2) учитывается в среднем,
с помощью введения множителя Лагранжа λ, который полагается не зависящим от
296
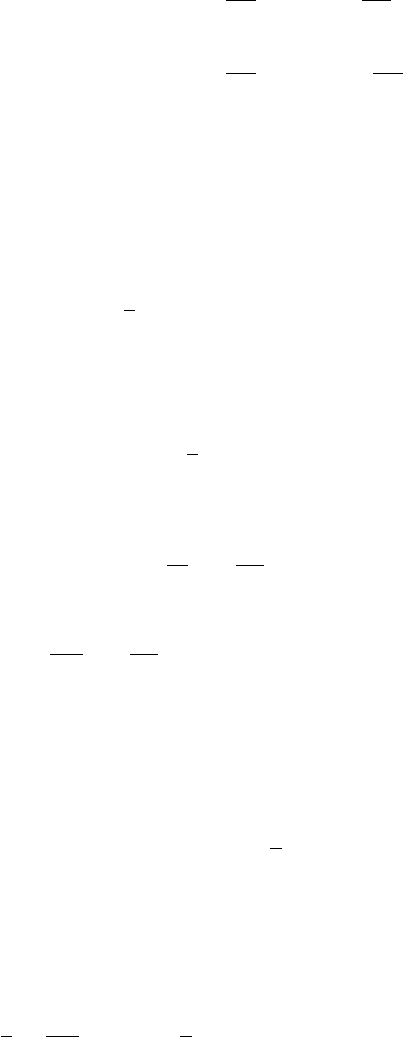
i. Аномальные средние hb
i↑
b
j↓
i, описывающие синглетное спаривание бозонов, явля-
ются параметрами ближнего порядка. Возможность дальнего порядка, характери-
зуемого волновым вектором Q, соответствует бозе-эйнштейновской конденсации с
квазиимпульсом k = ±Q/2 Удобно ввести взаимодействие с малым внешним маг-
нитным полем H. Тогда преобразование Боголюбова
b
Q/2+k↑
= cosh
Θ
k
2
α
k
− sinh
Θ
k
2
β
†
−k
b
Q/2−k↓
= cosh
Θ
k
2
β
−k
− sinh
Θ
k
2
α
†
k
(P.4)
приводит гамильтониан Гейзенберга к диагональной форме
H
d
=
X
k
³
E
α
k
α
†
k
α
k
+ E
β
k
β
†
k
β
k
´
(P.5)
где, для квадратной решетки с параметром a
0
= 1,
E
α,β
k
= E
k
∓
µ
1
2
H − 2|J|hS
z
i
¶
, E
k
= (λ
2
− γ
2
k
)
1/2
(P.6)
sinh Θ
k
= γ
k
/E
k
, cosh Θ
k
= λ/E
k
(P.7)
где
γ
k
=
1
2
γ(sin k
x
+ sin k
y
)
Уравнения для λ и γ, которые получаются из (P.7), имеют вид
2S + 1 =
1
N
X
k
λ
E
k
(1 + N
kα
+ N
kβ
) (P.8)
1 =
1
2N
X
k
|J|
E
k
(sin k
x
+ sin k
y
)
2
(1 + N
kα
+ N
kβ
) (P.9)
где N
kα,β
= N
B
(E
α,β
k
), N – число узлов, которое в рассматриваемой задаче нужно
писать явно.
При T = 0 мы получаем λ = γ, а N
kα
(но не N
kβ
) содержит конденсатный член
при E
α
k
= 0, т.е.
k = ±Q/2, E
k
=
1
2
H − 2JhS
z
i ∼ H (P.10)
Поэтому получаем
N
±Q/2
= NhS
z
i = NE
Q/2
n
B
/λ (P.11)
где 2n
B
– плотность сконденсировавшихся бозонов. Уравнение (P.8) дает
n
B
= S +
1
2
−
1
2N
X
k
·
1 −
1
4
(sin k
x
+ sin k
y
)
2
¸
−1/2
= S − 0.197 (P.12)
поэтому n
B
равняется подрешеточной намагниченности в основном состоянии нее-
левского антиферромагнетика
¯
S(0) с учетом нулевых спин-волновых поправок.
297
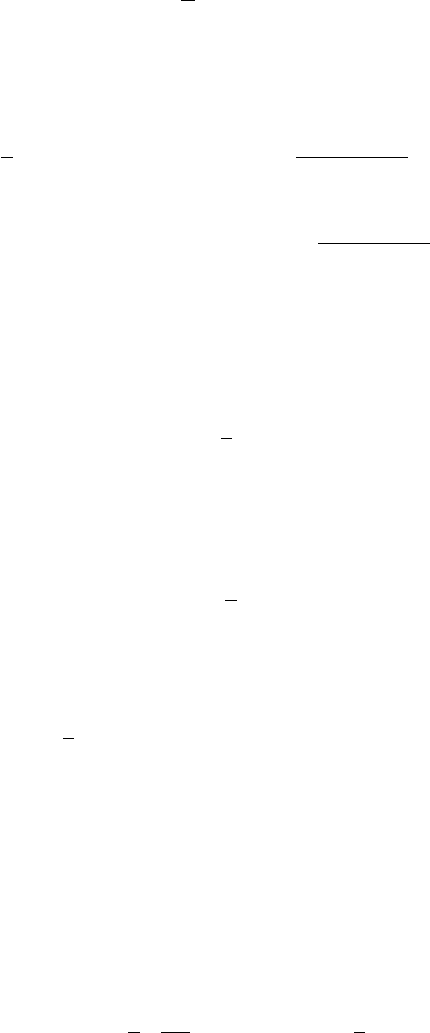
При конечных T спектр бозонов (P.6) содержит щель и конденсация отсутсвует.
Тогда мы с самого начала можем считать H = 0, N
kα,β
= N
k
.
Рассмотрим спиновую спектральную плотность
K
q
(ω) = −
1
π
N
B
(ω)ImhhS
q
|S
−q
ii
ω
(P.13)
в представлении швингеровских бозонов. Спиновая функция Грина выражается че-
рез поляризационные операторы невзаимодействующих бозонов α и β, и мы полу-
чаем
K
q
(ω) =
1
4
X
k
X
ν,µ=α,β
½
(2 − δ
µν
) cosh
2
Θ
k
− Θ
k+q
2
N
kµ
(1 + N
k+qν
)
×δ(ω + E
ν
k+q
− E
µ
k
) + (1 + δ
µν
) sinh
2
Θ
k
− Θ
k+q
2
[N
kµ
N
k+qν
× δ(ω − E
ν
k+q
− E
µ
k
) + (1 + N
kµ
)(1 + N
k+qν
)δ(ω + E
ν
k+q
+ E
µ
k
)]
ª
(P.14)
Как следует из (P.11), (P.14), спектральная плотность содержит при T = 0, H → 0
дельта-функционный вклад
δK
q
(ω) =
3
2
n
2
B
Nδ
qQ
δ(ω) (P.15)
Множитель 3/2 в (P.15) должен быть на самом деле опущен, поскольку он является
артефактом теории среднего поля которая дает из-за неаккуратного учета условия
(P.2)
hS
2
i
i =
3
2
S(S + 1)
нарушая тим самым соответствующее правило сумм на узле.
При конечных температурах мы получаем
E
2
k
=
1
2
λ
2
£
(k ∓ Q/2)
2
+ ξ
−2
¤
, k → ±Q/2 (P.16)
где коррелляционная длина равна
ξ ∼ exp(πλn
B
/2T ) (P.17)
При q = Q интеграл в (P.14) “почти” расходится в точках k = ±Q/2 с обрезани-
ем на масштабе |k ∓ Q/2| ∼ ξ
−1
. Используя разложение N
k
∼
=
T/E
k
, представим
соответствующий сингулярный вклад в виде
δK
q
(ω) =
3
2
·
2T
πλ
ln ξ
¸
2
∆
q
∆
ω
≈
3
2
n
2
B
∆
q
∆
ω
(P.18)
где ∆
q
и ∆
ω
есть функции δ(q − Q) и δ(ω), размытые на масштабе ξ
−1
и ω
ξ
∼ J/ξ
соответственно. При T ¿ J получаем ω
ξ
¿ T , и мы можем принебречь размытием,
что дает формальное описание сильного ближнего порядка. Чтобы получить темпе-
ратурную зависимость коэффициента в (P.18) (“подрешеточной намагниченности”),
298
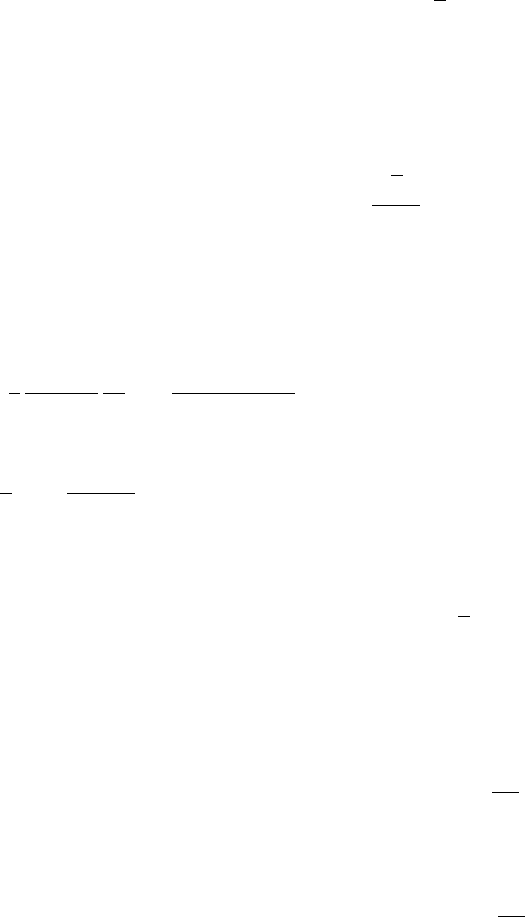
мы оценим интенсивность пика Орнштейна - Цернике при q = Q в статическом
корреляторе
S
eff
(T ) =
X
|q−Q|<q
0
hS
−q
S
q
i
1/2
(P.19)
где q
0
À ξ
−1
– волновой вектор обрезания. Используем результат скейлингового
рассмотрения [712], которое дает правильный предэкспоненциальный множитель:
ξ = C
ξ
exp
³
πc
¯
S(0)/
√
2T
´
(P.20)
где c – магнонная скорость, а C
ξ
∼
=
0.01/(2π) ¿ 1 - численный коэффициент. Под-
ставляя (P.20) в (P.19), (P.18) и принебрегая ln q по сравнению с ln C
ξ
, мы получаем
линейную зависимость [713]
S
eff
(T ) =
¯
S(0) −
√
2T
πc
|ln C
ξ
| (P.21)
Вклады в спектральную плотность от антиферромагнитных спиновых волн опре-
деляются членами, которые линейны по n
B
. Полагая E
k
→ 0, N
k
= T/E
k
, но сохра-
няя E
k+q
(и наоборот) и выполняя интегрирование по k, получаем
δ
1
K
q
(ω) =
3
2
T
E
q+Q/2
1
N
X
k
λ
2
− γ
k
γ
k+q
E
2
k
[(1+N
q+Q/2
)δ(ω+E
q+Q/2
)+N
q+Q/2
δ(ω−E
q+Q/2
)]
≈
3
2
n
B
µ
1 − ϕ
q
1 + ϕ
q
¶
1/2
{[1 + N
B
(ω
q
)]δ(ω + ω
q
) + N
B
(ω
q
)δ(ω − ω
q
)} (P.22)
где, для q, |q − Q| À ξ
−1
,
ω
q
= λ(1 − ϕ
2
q
)
1/2
≈ E
q+Q/2
, ϕ
q
≡
1
2
(cos q
x
+ cos q
y
) (P.23)
так что ω
q
– перенормированная магнонная частота.
Для сравнения рассмотрим применение представления Дайсона-Малеева (E.2) к
той же задаче. В случае двухподрешеточного антиферромагнетика оно имеет вид
S
−
l
= (2S)
1/2
a
†
l
, S
+
l
= (2S)
1/2
(1 −
1
2S
a
†
l
a
l
)a
l
S
z
l
= S − a
†
l
a
l
, l ∈ A
S
−
m
= (2S)
1/2
b
†
m
, S
+
m
= (2S)
1/2
b
†
m
(1 −
1
2S
b
†
m
b
m
)b
m
(P.24)
S
z
m
= −S + b
†
m
b
m
, m ∈ B
В самосогласованном подходе [624] нужно наложить на каждом узле условие hS
z
i =
0, т.е.
ha
†
l
a
l
i = hb
†
l
b
l
i = S (P.25)
299
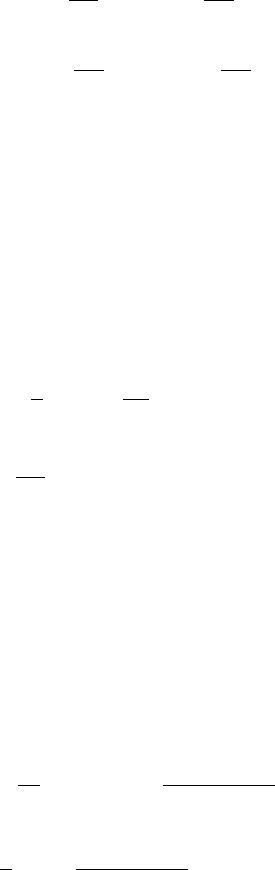
Используя преобразование Боголюбова
a
k
= cosh
Θ
k
2
α
k
− sinh
Θ
k
2
β
†
−k
b
†
−k
= cosh
Θ
k
2
β
†
−k
− sinh
Θ
k
2
α
k
(P.26)
мы диагонализуем гамильтониан и получаем
H =
X
k
ω
k
(α
†
k
α
k
+ β
†
k
β
k
) (P.27)
где
hα
†
k
α
k
i = hβ
†
k
β
k
i = N
k
= N
B
(ω
k
)
ω
k
= (λ
2
− γ
2
ϕ
2
k
)
1/2
, tanh 2Θ
k
= γϕ
k
/λ (P .28)
Здесь Σ
0
означает суммирование по приведенной зоне Бриллюэна. Уравнения для λ
и γ имеют вид
S +
1
2
=
X
k
0
λ
ω
k
(1 + 2N
k
) (P.29)
1 =
X
k
0
|J|
ω
k
(cos k
x
+ cos k
y
)(1 + 2N
k
) (P.30)
При T = 0 (в более общем случае, при наличии дальнего порядка), λ = γ + O(1/N),
поэтому спектр безщелевой. 1/N-поправки описывают Бозе-конденсацию:
¡
1 − γ
2
/λ
2
¢
2
= Nn
B
(P.31)
Как следует из условий (P.25) и структуры преобразования Дайсона-Малеева, спи-
новая корреляционная функция hS
+
q
S
−
−q
i обращается в нуль. Поэтому соответству-
ющая спектральная плотность принмает вид
K
q
(ω) = K
zz
q
(ω) =
1
N
X
k
0
½
cosh
Θ
k
− Θ
k+q
2
N
k
(1 + N
k+q
)
×δ(ω + ω
k+q
− ω
k
) +
1
2
sinh
2
Θ
k
− Θ
k+q
2
{N
k
N
k+q
δ(ω − ω
k+q
− ω
k
)
+ (1 + N
k
)(1 + N
k+q
)δ(ω + ω
k+q
+ ω
k
)]} (P .32)
Дельта-функционный вклад имеет форму
δK
q
(ω) = Nn
2
B
δ
qQ
δ(ω) (P.33)
В отличие (P.15), выражение (P.33) не содержит лишнего множителя 3/2. С дру-
гой стороны, в отличие от "изотропного"представления Швингера, представление
Дайсона-Малеева нарушает вращательную инвариантость даже в парамагнитной
фазе.
Версия самосогласованной спин-волновой теории (ССВТ), базирующаяся на
нелинейном бозонном представлении, дает щель в спин-волновом спектре в отсут-
ствие дальнего порядка. Это противоречит, например, точным результатам для од-
номерной решетки с полуцелым спином S, где спектр бесщелевой (для целых спинов,
300
