Ирхин В.Ю., Ирхин Ю.П. Электронная структура, корреляционные эффекты и физические свойства d - и f-переходных металлов и их соединений
Подождите немного. Документ загружается.

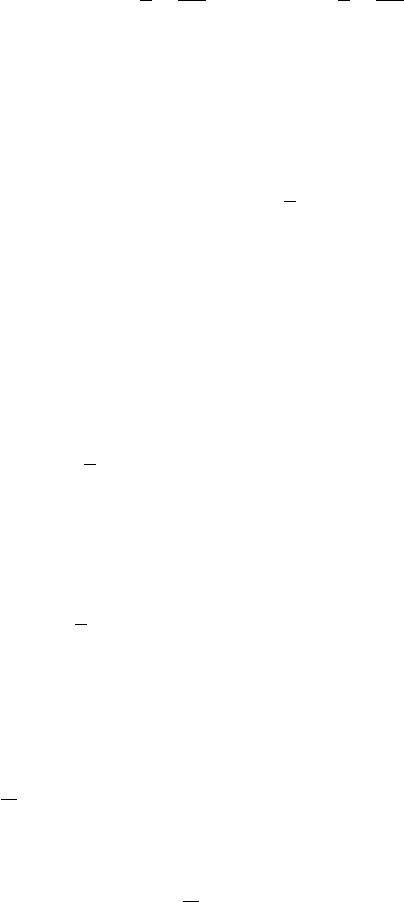
u
2
q
=
1
2
µ
C
q
ω
q
+ 1
¶
, v
2
q
=
1
2
µ
C
q
ω
q
− 1
¶
и получаем
H = const +
X
q
ω
q
β
†
q
β
q
+ ... (E.11)
где спин-волновой спектр имеет вид
ω
q
= (C
2
q
− D
2
q
)
1/2
= 2S{[J
Q
−
1
2
(J
Q+q
+ J
Q−q
)][J
Q
− J
q
]}
1/2
(E.12)
Частота спиновой волны имеет тенденцию стремиться к нулю и при q → 0, и при
q → Q, при этом q-зависимость линейна, в отличие от случая ферромагнетика (здесь
не обсуждается магнитная анизотропия, которая приводит к искажению спектра
спиновых волн при малых q, |q − Q| [15,16]). Используя теорему Вика для четверных
членов, которыми пренебрегли в Гамильтониане (E.9), можно получить поправки к
C
q
и D
q
из-за магнон-магнонного взаимодействия
δC
q
= −
1
2
X
p
(4J
Q
+ 2J
Q+q−p
+ 2J
Q−q−p
− 2J
p
− 2J
Q
(E.13)
−J
Q+q
− J
Q−q
− −2J
Q+p
)hb
†
p
b
p
i −
X
p
(J
Q+p
− J
p
)hb
†
p
b
−p
i
δD
q
= −
1
2
X
p
(J
Q+q
+ 2J
Q+p
+ J
Q−q
− 2J
q
− 2J
p
)hb
†
p
b
p
i
+
X
p
(J
Q+p
+ J
p
)hb
†
p
b
†
−p
i
Низкотемпературное поведение намагниченности подрешетки имеет следующий вид
S = hS
z
i = S − hb
†
bi = S −
X
q
£
u
2
q
N
q
+ v
2
q
(1 + N
q
)
¤
(E.14)
so that
δS(T ) ∼ −(T/T
N
)
2
Спин-волновой подход позволяет получить интерполяционное описание ферромаг-
нетика Гейзенберга во всем температурном диапазоне. Это было сделано Тяблико-
вым [357] с использованием метода функции Грина. Определим антикоммутаторную
(коммутаторную) двухвременную запаздывающую функция Грина для операторов
A и B [671]
hhA|Bii
±
E
=
Z
0
−∞
dte
iEt
h[e
iHt
Ae
−iHt
, B]
±
i, Im E > 0 (E.15)
Функция Грина (E.15) удовлетворяет уравнению движения
EhhA|Bii
±
E
= h[A, B]
±
i + hh[A, H]|Bii
±
E
(E.16a)
или
EhhA|Bii
±
E
= h[A, B]
±
i + hhA|[H, Bii
±
E
(E.16b)
221

и таким образом выражается через более сложные функции Грина. Как видно из
(E.16), удобно использовать коммутаторную функцию Грина в случае операторов
бозе-типа A, B (для которых коммутатор [A, B], который стоит в среднем, будет
"более простым"оператором), и антикоммутаторную - в случае операторов Ферми-
типа. В случаях свободных бозонов и фермионов, для которых Гамильтониан имеет
диагональную форму, уравнения (E.16) упрощаются и получаем
hhb
q
|b
†
q
ii
−
ω
=
1
ω − ω
q
, hhc
k
|c
†
k
ii
+
E
=
1
E − E
k
(E.17)
Вычисление функции Грина позволяет получить соответствующие термодинамиче-
ские средние, используя спектральное представление
hBAi = −
1
π
Z
∞
∞
dE
1
e
E/T
± 1
ImhhA|Bii
±
E+iδ
(E.18)
В частности, из (E.17) получаем
hb
†
q
b
q
i = N
B
(ω
q
), hc
†
k
c
k
i = f(E
k
) (E.19)
В общем случае, бесконечная последовательность уравнений (E.16) может быть
"расцеплена"выражением функции Грина с более высоким порядком через более
простые. В случае взаимодействующих квазичастиц функция Грина может быть
выражена через уравнение Дайсона
hhb
q
|b
†
q
ii
ω
= [ω − ω
q
− Π
q
(ω)]
−1
(E.20)
hhc
k
|c
†
k
ii
E
= [E − E
k
− Σ
k
(E)]
−1
Вещественная часть собственной энергии Σ(или поляризационного оператора Π))
дает энергетический сдвиг, а мнимая часть определяет затухание квазичастиц. При
условии, что гамильтониан взаимодействия содержит малый параметр, метод урав-
нений движения позволяет провести разложение по возмущению в удобном виде.
В частности, применяя оба уравнения (E.16), получим выражение для собственной
энергии
Σ
k
(E) = Λ
k
+ hh[c
k
, H
int
] − Λ
k
c
k
|[H
int
, c
†
k
] − Λ
k
c
†
k
ii
irr
E
,
Λ
k
= h
n
[c
k
, H
int
], c
†
k
o
i (E.21)
где символ "irr"означает, что расходящиеся вклады, содержащие знаменатели (E −
ε
k
)
n
, должны быть опущены при дальнейших вычислениях неприводимой функ-
ции Грина (E.21). В этой книге применяется метод двухвременной запаздывающей
функции Грина к различным многоэлектронным моделям, описывающим высоко-
коррелированные d- и f-системы. В теории переходных металлов, эта методика
очень полезна, так как приходится встречаться с операторами, которые не обла-
дают простыми коммутационными соотношениями, и таким образом стандартные
диаграммные разложения [27] неприменимы. Таковыми являются многоэлектронные
X-операторы Ферми и Бозе типа (Приложение A) и спиновые операторы (Приложе-
ние B). Ниже кратко опишем вывод уравнения Тябликова для намагниченности в
222
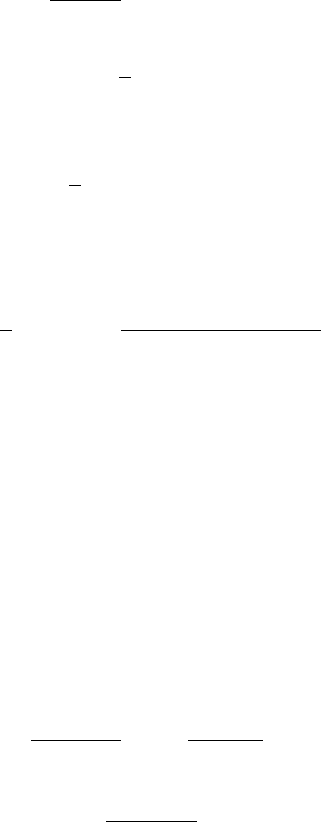
модели Гейзенберга для спина S = 1/2 (общий случай обсуждается в Приложении F
с использованием подхода X-операторов Хаббарда). Запишем уравнение движения
для коммутаторной поперечной спиновой функции Грина
(ω − H)hhS
+
q
|S
−
−q
ii
ω
= 2hS
z
i + 2
X
p
(J
p−q
− J
p
)hhS
z
p
S
+
q−p
|S
−
−q
ii
ω
Присутствие множителя 2hS
z
i по сравнению с (E.17) связано с небозевскими комму-
тационными соотношениями для операторов спина. Результат (E.22) имеет силу для
произвольного значения S.. Для S = 1/2, используя (E.18) и тождество Выполняя
простейшее расцепление для различных узлов решетки, получаем
hhS
+
q
|S
−
−q
ii
ω
=
2hS
z
i
ω − ω
q
, ω
q
= 2hS
z
i(J
0
− J
q
) + H (E.22)
S
z
i
=
1
2
− S
−
i
S
+
i
(E.23)
получаем самосогласованное уравнение для hS
z
i
hS
z
i =
1
2
[1 + 2
X
q
N
B
(ω
q
)]
−1
которое может быть преобразовано к виду
hS
z
i =
1
2
"
X
q
coth
2hS
z
i(J
0
− J
q
) + H
T
#
−1
(E.24)
Уравнение (E.24) отличается от уравнения в приближении среднего поля (4.14)
присутствием дисперсионной (q-зависимость) спектра возбуждения. Такой подход
удовлетворительно описывает термодинамику модели Гейзенберга и при высоких,
и при низких температурах, хотя члены более высокого порядка в низкотемпера-
турном разложении не вполне согласуются со строгими результатами Дайсона (в
частности, появляются паразитные T -члены в намагниченности). Многочисленные
попытки улучшить область спин-волнового описания, используя более сложные про-
цедуры расцепления (см. [357]), привели ухудшению интерполяции. Значения фер-
ромагнитной и парамагнитной температур Кюри в приближении Тябликова для про-
извольного значения S имеют вид
T
c
=
S(S + 1)
3
Ã
X
q
1
J
0
− J
q
!
−1
(E.25)
θ =
S(S + 1)
3
J
0
(E.26)
и несколько различаются (результат теории среднего поля (4.18) получен из (E.25)
усреднением знаменателя по q, то есть в самом низком порядке по 1/z). Соответ-
ствующие выражения для антиферромагнетика получаются из (E.25), (E.26) заме-
ной J
0
→ J
q
. В конце этого Приложения обсудим еще один метод в теории гейзен-
берговских магнетиков [672]. Чтобы учесть кинематические взаимодействия, в этом
223

подходе в представление Дайсона-Малеева (E.2) вводятся вспомогательные псевдо-
фермионные операторы c:
S
z
= S − b
†
b − (2S + 1)c
†
c, S
−
= (2S)
1/2
b
†
(E.27)
S
†
= (2S)
1/2
µ
1 −
1
2S
b
†
b
¶
b − 2(2S + 1)(2S)
1/2
bc
†
c
Функция распределения бездисперсионных фермионов оказывается следующей
h
c
†
i
c
i
i
=
−
N
B
((2
S
+ 1)
e
H
)
,
e
H
=
H
= 2
J
0
h
S
z
i
(E
.
28)
Видно, что псевдофермионные операторы исключают нефизические состояния, для
того чтобы экстраполяция к высоким температурам стала возможной. В частности,
пренебрегая дисперсией возбуждений спиновых волн, получаем из (E. 27), (E. 28)
hS
z
i = S − N
B
(
e
H) + (2S + 1)N
B
((2S + 1)
e
H) = S − B
S
(S
e
H/T ) (E.29)
Таким образом, получаем повторно уравнение для намагниченности в приближении
среднего поля (4.15).
224
Приложение F
Метод операторов Хаббарда в модели
Гейзенберга
Подход операторов Хаббарда в модели Гейзенберга Использование операторов Хаб-
барда дает возможность получить простым способом главные результаты теории
гейзенберговских магнетиков. В частности, этот формализм позволяет принять во
внимание сильную одноионную магнитную анизотропию в приближении нулевого
порядка [673-677]. Гамильтониан модели Гейзенберга с произвольной одноузельной
анизотропией имеет вид
H = −
X
ij
J
ij
S
i
S
j
+ H
a
= −
X
q
J
q
S
q
S
−q
+ H
a
(F.1)
H
a
=
X
i
ϕ(S
x
i
, S
y
i
, S
z
i
, H) (F.2)
где J
q
- Фурье компоненты обменных параметров, H - внешнее магнитное поле, ϕ
- произвольная функция. Следует заметить, что, как следует из результатов При-
ложения C, гамильтониан (F.1) с S → L описывает систему взаимодействующих
орбитальных моментов в промежуточном кристаллическом поле, H
a
имеет смысл
гамильтониана кристаллического электрического поля. Таким образом, анизотроп-
ная модель Гейзенберга может применяться к проблеме подавления орбитальных
моментов. Сначала рассмотрим ферромагнетик с легкой осью, для которого
H
a
= −
X
i
ϕ(S
z
i
) − H
X
i
S
z
i
(F.3)
Используем представление операторов момента через операторы Хаббарда (Прило-
жение B)
S
±
i
=
S
X
M=−S
γ
S
(±M)X
i
(M ± 1, M), S
z
i
=
S
X
M=−S
MX(M, M)
γ
S
(M) ≡ [(S − M)(S + M + 1)]
1/2
(F.4)
Тогда гамильтониан анизотропии примет диагональную форму
H
a
= −
X
iM
[ϕ(M) + HM]X
i
(M, M) (F.5)
225

Удобно ввести коммутаторную функцию Грина
G
q
(ω) = hhS
+
q
|S
−
−q
ii
ω
, (F.6)
G
qM
(ω) = hhX
q
(M + 1, M)|S
−
−q
ii
ω
Запишем уравнение движения
(ω − H − ϕ(M + 1) + ϕ(M) − 2J
0
hS
z
i)G
qM
(ω)
= γ
S
(M)(N
M+!
− N
M
)[1 − J
q
G
q
(ω)] (F.7)
в котором выполним простейшее расцепление, соответствующее расцеплению Тяб-
ликова на различных узлах (E.22),
N
M
= hX(M, M)i
После суммирования по M получаем
G
q
(ω) =
Φ
S
(ω)
1 + J
q
Φ
S
(ω)
(F.8)
где
Φ
S
(ω) =
X
M
γ
2
S
(M)(N
M+1
− N
M
)
ω − H − ϕ(M + 1) + ϕ(M) − 2J
0
hS
z
i
(F.9)
Структура выражения (F.8) напоминает функцию Грина в теории коллективизи-
рованного электронного магнетизма (см. Приложения G,H). Спектр возбуждений
определяется уравнением
1 + J
q
Φ
S
(ω) = 0 (F.10)
и содержит 2S ветви. Выражения (F.7), (F.8) позволяют вычислить числа заполне-
ния N
M
и получить самосогласованное уравнение для намагниченности
hS
z
i =
X
M
MN
M
(F.11)
Для простоты ограничимся анализом этого уравнения в изотропном случае, кото-
рый приводит к (E.22). Используя правила умножения для операторов Хаббарда и
спектральное представление (E.18), получаем
hS
−
i
X
i
(M + 1, M)i = γ
S
(M)N
M
(F.12)
= γ
S
(M)(N
M+1
− N
M
)
X
q
N
B
(ω
q
)
Тогда система для N
M
имеет вид
N
M
= (N
M+1
− N
M
)P
S
,
X
M
N
M
= 1, P
S
≡
X
q
N
B
(ω
q
) (F.13)
Решая эту систему, получим уравнение для hS
z
i [675]
hS
z
i = SB
S
(−S ln(P
S
/[1 + P
S
])) (F.14)
226

Уравнение (F.14) имеет вид, который несколько отличается от стандартного [357],
и является более удобным. Теперь обсудим общий случай [675-677]. Гамильтониан
(F.2) может быть диагонализован, что дает
H
a
|ψ
µ
i = E
µ
|ψ
µ
i (F.15)
Собственные функции ψ
µ
могут быть выражены через собственные функции |Mi
оператора S
z
:
|ψ
µ
i =
X
M
c
µM
|Mi (F.16)
Тогда спиновые операторы можно представить через операторы Хаббарда следую-
щим образом
S
+
i
=
X
µµ
/
M
c
µ
/
M
c
∗
µ,M+1
γ
S
(M)X
i
(µ, µ
/
) (F.17)
S
z
i
=
X
µµ
/
M
c
µ
/
M
c
∗
µ,M
MX
i
(µ, µ
/
) (F.18)
Для H||hS
z
i в простейшем приближении среднего поля можно учесть межузельное
обменное взаимодействие, заменяя H на эффективное поле
e
H = H + 2J
0
hS
z
i (F.19)
Тогда числа заполнения N
M
получаются следующим образом
N
M
=
X
µ
|c
µM
|
2
N
µ
=
P
µ
|c
µM
|
2
exp(−E
µ
/T )
P
µ
exp(−E
µ
/T )
(F.20)
Рассмотрим ферромагнетик типа легкая плоскость, для которого
H
a
= 2D
X
i
(S
x
i
)
2
− H
X
i
S
z
i
, D > 0 (F.21)
Результаты оказываются существенно разными для целочисленных и полуцелых
спинов. (Такая разница типична для квантовых спиновых систем, см., например,
[678]). Это происходит из-за того, что основное состояние иона с целым S - синглет,
и возбужденные магнитные состояния отделены энергетической щелью. В частно-
сти, для S = 1 имеем [673]
|ψ
1,3
i = cos θ| ± 1i ± sin θ| ∓ 1i (F.22)
E
1,3
= D ∓ (H
2
+ D
2
)
1/2
, E
2
= 2D
где
cos 2θ =
H
(H
2
+ D
2
)
1/2
, sin 2θ = −
D
(H
2
+ D
2
)
1/2
(F.23)
Согласно (F.10), (F.20) уравнение для намагниченности имеет вид
hS
z
i =
cos 2
e
θ sinh[(
e
H
2
+ D
2
)
1/2
/T ]
cosh[(
e
H
2
+ D
2
)
1/2
/T ] +
1
2
exp(−D/T )
(F.24)
227
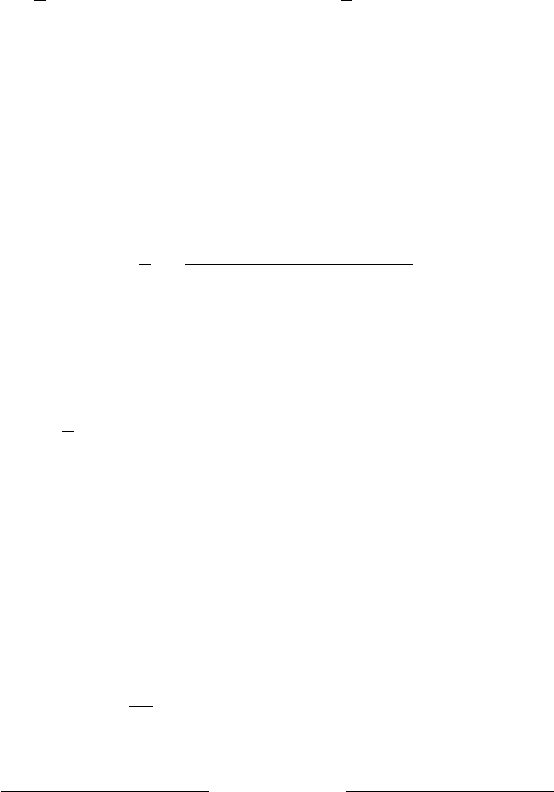
При нулевых температуре и магнитном поле получаем
hS
z
i =
½
[1 − (D/2J
0
)
2
]
1/2
, D < 2J
0
0 , D > 2J
0
(F.25)
Таким образом, при D > 2J
0
основное состояние |ψ
1
i - наложение синглетных состо-
яний |1i и |−1i (sin θ = cos θ), и ферромагнитное упорядочение подавляется. Сильно
анизотропные системы с легкой плоскостью проявляют также нетривиальное пове-
дение намагниченности при изменении магнитного поля [679,680], что напоминает о
поведении удельной проводимости Холла в случае квантового эффекта Холла [681].
Для полуцелых S, основное состояние упорядоченно при произвольных D. Однако,
значение намагниченности уменьшается из-за смешивания состояний с различными
значениями M полем анизотропии. Так, для S = 3/2 имеем
|ψ
1,4
i = cos θ
±
| ± 3/2i ∓ sin θ
±
| ∓ 1/2i (F.26)
|ψ
2,3
i = cos θ
∓
| ± 1/2i ∓ sin θ
∓
| ∓ 3/2i
E
1,4
=
1
2
(5D ∓ H) ∓ E
±
, E
2,3
=
1
2
(5D ± H) ∓ E
∓
где
cos θ
±
= [H ± D + E
±
]/[3D
2
+ (H ± D + E
±
)
2
]
1/2
E
±
= [(H ± D)
2
+ 3D
2
]
1/2
(F.27)
Можно видеть, что нижний уровень |ψ
1
i - смесь состояний с M = 3/2 и M = −1/2.
Намагниченность при T = 0 равняется
hS
z
i =
3
2
−
6D
2
3D
2
+ (
e
H + D +
e
E
+
)
2
(F.28)
При D À J получаем из (F.28) hS
z
i = 1, и основное состояние - дублет.
Для кубических анизотропных ферромагнетиков имеем
H
a
= −
1
2
K
X
i
£
(S
x
i
)
4
+ (S
y
i
)
4
+ (S
z
i
)
4
¤
− H
X
i
S
z
i
(F.29)
При S ≤ 3/2 одноионная кубическая анизотропия не проявляется из-за кинематиче-
ских причин. Для S = 2 получаем
|ψ
1,2
i = cos θ| ± 2i ± sin θ| ∓ 2i, |ψ
3,4
i = | ± 1i, |ψ
S
i = |0i
E
1,2
= C ∓ E, E
3,4
= C + K ∓ H, E
S
+ C − K (F.30)
C = −
21
2
K, E = (H
2
+ K
2
)
1/2
где
cos θ =
2H + E
[K
2
+ (2H + E)
2
]
1/2
, sin θ =
D
[K
2
+ (2H + E)
2
]
1/2
(F.31)
228

Рассмотрим случай K > 0, так что направление легкого намагничивания совпадает
с осью z. Тогда основное состояние - |ψ
1
i. . Уравнение для намагниченности имеет
вид
hS
z
i =
2 cos 2
e
θ sinh(eε/T) + exp( −K/T ) sin(
e
H/T )
cosh(eε/T ) +
1
2
exp(K/T ) + exp( −K/T ) cos(
e
H/T )
(F.32)
Намагниченность основного состояния записывается следующим образом
hS
z
i = 2[1 − (K/8J
0
)
2
]
1/2
(F.33)
и исчезает при K > 8J. Ферромагнитное упорядочение при большом значении K так-
же не происходит для S = 4. Таким образом, орбитальные моменты L = 2 и L = 4
подавляются кубическим кристаллическим полем. Внутриатомное орбитальное об-
менное взаимодействие, которое требуется для их размораживания, определяется из
(F.19), (F.32). Для S = 5/2, 3 и 7/2 основное состояние оказывается всегда упорядо-
ченным, значения hS
z
i при T = 0 в пределе сильной анизотропии будут 11/6, 3/2 и
7/6 соответственно [676].
229
Приложение G
Электрон-магнонное взаимодействие
в магнитных металлах
В этом Приложении будет вычислен спектр одночастичных и спин-волновых воз-
буждений в металлических магнетиках. С этой целью используем многоэлектрон-
ные модели, которые позволяют описывать влияние межэлектронных корреляций.
Простейшая модель такого типа - модель Хаббарда. В случае невырожденной зоны
ее гамильтониан имеет вид
H =
X
kσ
t
k
c
†
kσ
c
kσ
+ H
int
, (G.1)
H
int
= U
X
i
c
†
i↑
c
i↑
c
†
i↓
c
i↓
где U - параметр отталкивания на узле. Модель Хаббарда широко использовалась
для рассмотрения коллективизированного электронного ферромагнетизма, так как
она учитывает самую большую часть кулоновского взаимодействия - внутриатом-
ную. Несмотря на очевидную простоту, эта модель содержит очень богатую физику
и ее строгое исследование является весьма трудной проблемой.
Помимо модели Хаббарда, для теоретического описания магнитных металлов
иногда удобно использовать s-d(f) обменную модель. Модель s-d обмена была снача-
ла предложена для переходных d-металлов, чтобы рассмотреть особенности их элек-
трического сопротивления [265]. Эта модель постулирует существование двух элек-
тронных подсистем: коллективизированных "s-электронов", которые играют роль
носителей тока, и локализованных "d-электронов", которые дают главный вклад в
магнитный момент. Такое предположение едва ли может быть количественно под-
тверждено для d-металлов, но все же оно может быть полезным при качественном
рассмотрении некоторых физических свойств (особенно явлений переноса). В то же
самое время, s-f обменная модель о беспечивает хорошее описание магнетизма в ред-
коземельных металлах и их соединениях с хорошо локализованными 4f-состояниями.
Гамильтониан s-d(f) модели в простейшей форме имеет вид
H =
X
kσ
t
k
c
†
kσ
c
kσ
−
X
q
J
q
S
−q
S
q
+ H
int
≡ H
s
+ H
d(f)
+ H
int
(G.2)
230
