Ирхин В.Ю., Ирхин Ю.П. Электронная структура, корреляционные эффекты и физические свойства d

Подождите немного. Документ загружается.

В присутствии спин-орбитальной связи, мы должны рассматривать функции с

определенным полным угловым моментом J = L + S. В приближении Рессела-

Саундерса мы получаем

|SLJM

i = Ψ

SLJM

µM

Sµ,LM

|SLµMi (B.5)

а соответсвующие ME операторы рождения принимают вид

SLJM

µM

Sµ,LM

SLµM

(B.6)

Матричные элементы полного углового момента на мультиплете с фиксированным

J равны

hJM|J

|JM

i =

J (J + 1)C

,1q

(B.7)

Циклические компоненты вектора I = S, L, J выражаются через операторы Habbard

[(I − M) (I + M + 1)]

1/2

X (M + 1, M) (B.8)

−

[(I − M + 1) ( I + M)]

1/2

X (M − 1, M)

MX (M, M)

При переходе от обменных гамильтонианов, которые выражены через МЕ опера-

торы, к представлению момента импульса, требуются обратные преобразования от

X-операторов к операторам момента. Чтобы получить их, мы можем записать выра-

жения для всех степеней (I

)

где k = 0...2I (высшие степени не являются линейно

независимыми) и решить эту систему (2I + 1)

уравнений, что очень сложно. Более

удобно использовать неприводимые тензорные операторы

(k)

,kq

X (IM, IM

) (q = −k...k) (B.9)

поэтому

S (S + 1)S

(1)

(B.10)

(1)

L (L + 1)L

(1)

Операторы (B.9) связаны с эквивалентными операторами Стивенса в теории кри-

сталлического поля (см. Раздел.1.3). Используя соотношения ортогональности для

коэффициентов Клебша-Гордана, легко получить требуемые обратные соотношения

X (IM, IM

) =

,kq

(k)

(B.11)

Коммутационные соотношения операторов (В.9) принимают вид

(k)

, I

(k)

]

−

(−1)

− (−1)

k+k

k k

I I I

([K

] [I])

1/2

kq,k

)

201

где

. . .

являются 6j-символами. Явные выражения для неприводимых тен-

зорных операторов через обычные операторы момента сведены в таблицы [41,43].

Помимо этого, можно применять при аналитических вычислениях рекуррентную

формулу

(−1)

([k − p][p][I])

1/2

k − p p k

I I I

(k)

= [I

(k−p)

× I

(p)

]

(k)

(B.12)

где тензорное произведение ранга c определяется следующим образом

(a)

× B

(b)

]

(c)

αβ

cγ

aα,bβ

(a)

(b)

(B.13)

Чтобы выразить X-операторы, связывающие термы с различными L, S, J можно

использовать “ гиперболические "операторы, которые изменяют значение момента

непосредственно [656]. Они удовлетворяют коммутационным соотношением

, K

] = ∓K

, [K

, K

−

] = 2K

(B.14)

и имеют отличные от нуля матричные элементы

hJM|K

|J − 1Mi = [(J + M) (J − M)]

1/2

(B.15)

hJM|K

|JMi = J +

Эта проблема обсуждается также Поповым и Логиновым [657].

При переходе от LS-представления к J-представлению для мультиплета с дан-

ным J, мы должны выразить произведение L

(k)

(κ)

через операторы J

(p)

. Используя

(A.11), (B.6) и суммируя произведения четырех коэффициентов Клебша-Гордана с

использованием 9j-символов мы получаем

(κ)

(k)

P ρ







J S L

p κ k







([S][L][J][p])

1/2

P ρ

κξ,kq

(P )

(B.16)

Обратите внимание, что p + κ + k четное (в противоположном случае, 9j-символ в

(B. 15) обращается в ноль из-за свойств симметрии). Для k = 0 или κ = 0 9j-символ

упрощается, так, что мы получаем

(κ)

= (−1)

J+S+L+κ

([S] [J])

1/2

J S L

S J κ

(κ)

(B.17)

(k)

= (−1)

J+S+L+k

([L] [J])

1/2

J L S

L J k

(k)

(B.18)

В частности, при κ = 1 или k = 1 подстановка явных значений 6j-коэффициентов

дает

S = (g − 1)J (B.19)

L = (2 − g)J (B.20)

202

где

g = 1 +

(LS)

= 1 +

J (J + 1) − S ( S + 1) − L (L + 1)

2J (J + 1)

- фактор Ланде. Таким образом известная формула де Женна (B.19) (см. Раздел

4.7) получена из общего соотношения (B.16).

Теперь мы обсудим другой подход к описанию произведений Ферми операторов.

Так как матричные элементы операторов рождения Ферми a

lmσ

(A.10) пропорцио-

нальны коэффициентам Клебша-Гордана, эти операторы могут рассматриваться как

2(2l + 1) компоненты двойного тензорного оператора, действующего в спиновом и

орбитальном пространствах. При вычислении матричных элементов произведений

фермиевских операторов на одном узле, удобно ввести для каждой оболочки двой-

ные неприводимые тензорные операторы с компонентами

(κk)

ξq

σσ

,kq

1/2σ

,κξ

lmσ

(B.21)

(мы использовали определение, слегка отличное от [32]). Любой оператор вида

F =

где

f - произвольный одноэлектронный оператор, может быть представлен через

операторы (B.21). В частности,

(00)

mσ

lmσ

= ˆn (B.22)

- оператор числа частиц в оболочке. Циклические компоненты операторов полного

спинового и орбитального моментов (1.7) имеют вид (ср. (B.10))

√

(10)

(B.23)

l (l + 1)W

(01)

(B.24)

а внутреннее скалярное произведение

3l (l + 1)

(−1)

(11)

q,−q

(B.25)

пропорционально оператору спин-орбитальной связи.

Операторы (B.21) при k + κ > 1, в отличие от операторов (B.23), (B.24), имеют

ненулевые матричные элементы между термами с различными S и L и они, вообще

говоря, не приведены к произведению операторов момента (B.9). Однако, соответ-

ствующие соотношения могут быть быть установлены для фиксированного терма с

определенным L, S (или J). Вычисляя матричные элементы произведения Ферми

операторов с учетом (3.10) мы получим в соответствии с теоремой Вигнера-Эккарта

hSLµMα|W

(κk)

ξq

i (B.26)

203

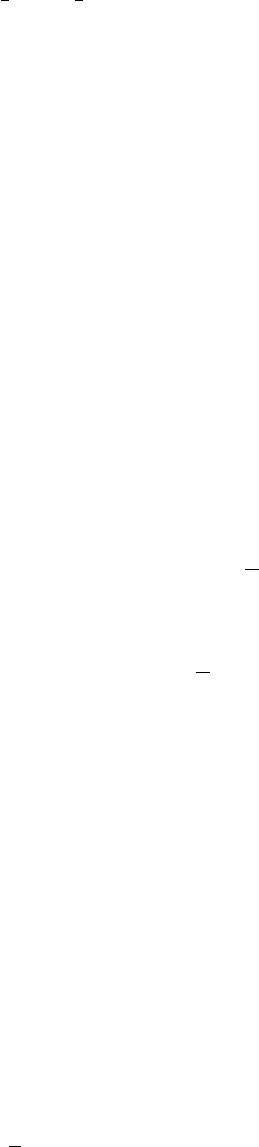
= ([S] [L])

−1/2

,kq

hSLα|W

(κk)

где приведенные матричные элементы имеют вид

hSLα||W

(κk)

||S

i = n (2 [l] [S] [S

] [L] [L

])

1/2

(B.27)

{

L¯α

}

SLα

L¯α

S S

¾½

l k l

L L

(−1)

1/2+l+S+L+

S+

L+κ+k

hSLα||W

(0k)

||S

i = nδ

([l] [S] [L] [L

])

1/2

(B.28)

{

L¯α

}

SLα

L¯α

l k l

L L

(−1)

l+L+

L+k+1

Они могут быть найдены в существующих таблицах (см., также, [10, 659]). Поэтому,

для терма мы получим

(κk)

= ([S] [L])

1/2

hSLα||W

(κk)

||SLαiS

(κ)

(k)

(B.29)

Сравнивая (B.27), (B.29) с (B.3), (B.4), (B.23), (B.24) можно заметить что подход

двойного неприводимого тензорного оператора приводит к суммированию генеало-

гических коэффициентов при k = 0, κ = 1 или k = 1, κ = 0 [660]. Мы увидим

в Дополнении D что это в свою очередь приводит к упрощению некоторых чле-

нов в обменном гамильтониане. В частности, подставляя значения 6j-символов в

SLα = S

, мы выводим

{

L¯α

}

SLα

L¯α

(−1)

S−

S+1/2

[S]

−1

(S 6= 0) (B.30)

{

L¯α

}

SLα

L¯α

L + 1

= l (l + 1) +

1 −

L (L + 1) (L 6= 0) (B.31)

Формализм двойного неприводимого тензорного оператора может быть обобщен

на тройные тензорные операторы a

(qls)

(q = s = 1/2) с компонентами

(qls)

1/2mσ

= a

lmσ

(B.32)

(qls)

−1/2mσ

= (−1)

l+s−m−σ

lmσ

а операторы составлены из

(Λκk)

λξr

ϕϕ

σσ

qϕ

,Λλ

Sσ

,κξ

,kr

(qls)

ϕmσ

(qls)

(B.33)

В частности, для κ = 0, k = 0, Λ = 1 мы получаем операторы квазиспина с компо-

нентами

mσ

(−1)

l+1/2−m−σ

lmσ

l−m−σ

(B.34)

204

= −

2l + 1 −

mσ

lmσ

которые удовлетворяют обычным коммутационным соотношениям для спиновых

операторов. Обратите внимание что оператор Q

совпадает с точностью до чис-

лового множителя с оператором рождения (2.14) для двух электронного синглета

с нулевым L из

S состояний и добавляет подобную пару к конфигурации l

n−2

Значение квазиспина для определенной последовательности термов эквивалентна

максимальному значению Q

Q =

(2l + 1 − v) (B.35)

где v - квантовое число сеньорити Рака, (n−v)/2 - число замкнутых электронных пар

с нулевым спином и орбитальным моментом для данного терма. Используя теорему

Вигнера-Эккарта в квазиспиновом пространстве можно использовать дополнитель-

ную симметрию МЕ проблемы (в частности, представить зависимость приведенных

матричных элементов и генеалогических коэффициентов от числа электронов в v

терме) [32]. Этот формализм может быть полезен в теории твердого тела при рас-

смотрении флуктуации заряда. Дальнейшее приложения теории групп для класси-

фикации многоэлектронных состояний обсуждается в книге [65].

205

Приложение C

Многоэлектронный гамильтониан

кристалла

Для того чтобы вывести многоэлектронные (ME) модели необходимо сначала рас-

смотреть точный Гамильтониан ME системы.

H =

−

¯h

∆

+ V (r

)

i6=j

− r

(C.1)

где V (r) - периодический кристаллический потенциал. В дальнейшем мы перейдем

к представлению вторичного квантования. Чтобы проделать это нужно иметь орто-

гональный набор одноэлектронных волновых функций. Однако, атомные волновые

функции

lmσ

(x) = ϕ

(r)χ

(s) = R

(r)Y

(ˆr)χ

(s) (C.2)

(s - спиновая координата, R

- радиальная волновая функция, Y – сферическая

функция, ˆr = (θ, φ)) не удовлетворяют этому условию для различных узлов ν. Неор-

тогональность - одна из наиболее трудных проблем в теории магнетизма [656,661].

Мы используем процедуру ортогонализации, предложенную Боголюбовым [651]. С

точностью до первого порядка по перекрытию атомных волновых функций ортого-

нализованные функции имеют вид

νlm

(r) = ϕ

νlm

(r) −

6=ν

(r)

∗

)ϕ

νlm

(r) (C.3)

Поправки от неортогональности можно не учитывать при рассмотрении одно-

узельных и двухузельных матричных элементов кулоновского (но не обменного)

взаимодействия.

Тогда мы получим Гамильтониан полярной модели [651,662,663] в общем случае

вырожденных зон

H =

νlmσ

†

νlmσ

6=ν

, l

†

(C.4)

, l

†

206

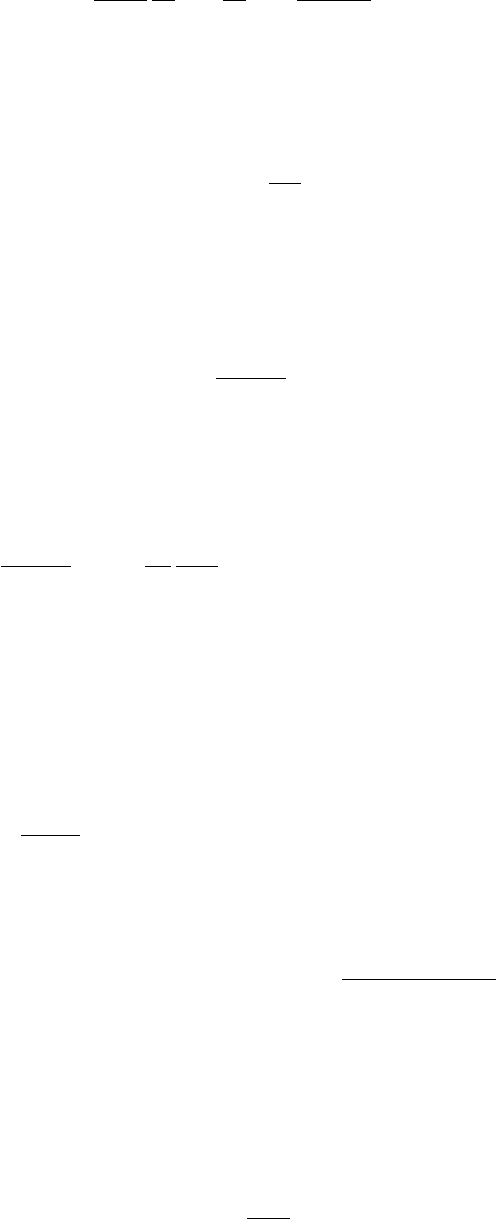
Здесь мы использовали ортогональность спиновых волновых функций χ

(s),

∞

drR

(r)

−

2mr

l ( l + 1)

2mr

+ v(r)

(r) (C.5)

- одноэлектронные уровни в центральном потенциале для узла v(r) (мы пренебрегаем

влиянием потенциалов других атомов, например эффектами кристаллического поля)

, l

) =

drψ

∗

(r)

−

¯h

∆ + V (r)

(r) (C.6)

- матричные элементы переноса между узлами ν

and ν

, l

) (C.7)

drdr

∗

(r)ψ

∗

)

|r − r

(r)ψ

)

- матричные элементы электростатического взаимодействия. Рассмотрим электро-

статическое взаимодействие между двумя атомными оболочками на одном узле

= ν

. Мы используем стандартное разложение

|r − r

∞

p=0

4π

[p]

p+1

q=−p

(ˆr)Y

(ˆr

) (C.8)

и выражение для матричных элементов сферических гармоник

sin θdθ

2π

dϕY

∗

(ˆr)Y

(ˆr) (C.9)

][l

]

4π[l

]

1/2

0,l

≡

Величины

C обращаются в ноль при четных l

+ l

а для l

+ l

= 2g можно

получить

0,l

= (−1)

]

1/2

g!{(2g + 1)}

−1/2

i=1

{(2g − 2l

)!}

1/2

(g − l

Проводя интегрирование, мы получаем для кулоновских членов (l

= l

, l

= l

)

coul

) =

0,p0

(p)

)(W

(0p)

) (C.10)

где

(p)

) = e

p+1

) (C.11)

207

– параметры Slater, неприводимые тензорные операторы W приведены в (B.21) а

скалярное произведение определяется

(a)

(−1)

(a)

−α

≡ (−1)

[a]

1/2

(a)

× B

(a)

]

(0)

(C.12)

Гамильтониан (C.10), с использованием (B.29), может быть выражен через много-

электронные операторы Хаббарда (B.29) (см. Приложение D).

Для обменных интегралов мы получаем

, l

) =

4π

[p]

,pq

(p)

)

где

(p)

) = e

)

p+1

) (C.13)

Преобразуя произведение коэффициентов Клебша-Гордана

,pq

kµ

,pq

(−1)

k−µ

(C.14)

мы выводим

exch

) = −

kpκ

(−1)

[k][κ]

]

1/2

(C.15)

0,p0

(p)

)

(κk)

Для k = 0 мы получаем из (B.22), (B.23) межатомный обменный гамильтониан

(κ0)

exch

) = −

]

1/2

0,p0

(p)

)[n

+ 4(S

)] (C.16)

а для κ = 0, k = 1 из (B.24) орбитальный обменный гамильтониан

(01)

exch

) = −

0,p0

+ 1) + l

+ 1) − p(p + 1)

+ 1)l

+ 1)[l

]

(p)

)(L

) (C.17)

В случае электростатического взаимодействия между электронами одной оболоч-

ки, F = G, поэтому мы представляем Гамильтониан в обоих формах (C.10) и (C.15).

Таким образом

H(l) =

0,p0

(p)

(ll)

(0p)

) − n

(C.18)

где второй член в квадратных скобках появляется из-за условия i 6= j в (C.1). В ME

представлении, Гамильтониан (C.18) принимает квазидиагональный вид. Вычисляя

матричные элементы скалярного произведения мы получаем

H(l) =

SLµM

αα

X(SLµMα, SLµMα

)

208

где

αα

SLMµ

0,p0

(p)

(l l){[S]

−1

[L]

−1

L¯α

hSLαkW

(0p)

L¯αi (C.19)

×hSLα

(0p)

L¯α − δ

αα

ni}

а приведенные матричные элементы даются (B.27). Если присутствует несколько

ME термов с одинаковыми значениями L,S (что типично для d-и f- электронов),

то требуется дополнительная диагонализация. Сохраняя в (C.19) вклады только с

p = 0 мы получаем

n(n − 1)F

(0)

(l l) (C.20)

Вклады с p = 2, 4... дают зависимость энергии термов от ME квантовых чисел S, L

в соответствии с правилом Хунда.

Выражения (C.10), (C.16), (C.18) сводят проблему электростатического взаимо-

действия между электронами к вычислению интегралов Slater. Они могут рассмат-

риваться как параметры, которые должные быть найдены из экспериментальных

данных (такая процедура часто используется в атомной спектроскопии). В этом

случае, волновые функции, которые входят в интегралы Slater, могут быть рассчи-

таны самосогласованным образом из соответствующих интегро-дифференциальных

уравнений [20]. Рассмотрим однозонный гамильтониан кристалла в многоэлектрон-

ном представлении. Из-за одноузельного кулоновского отталкивания и межузельно-

го переноса электронов (который принимается во внимание в модели Hubbard) мы

учтем электронный перенос относящийся к матричным элементам электростатиче-

ского взаимодействия (C.7) для ν

6= ν

, ν

= ν

. Ограничимся членами с ν

= ν

или ν

= ν

(трехузельные члены меньше, благодаря убыванию Coulomb взаимодей-

ствия с расстоянием). Используя (B.21), (C.19) и принимая во внимания поправки

от неортогональности мы получаем

H =

νΓ

(Γ, Γ) +

6=ν

n−1

−1

(Γ

n−1

, Γ

−1

) (C.21)

×X

(Γ

n−1

(Γ

−1

)

где

(Γ

n−1

, Γ

−1

) = (nn

)

1/2

n−1

−1

(C.22)

n−1

,γ

−1

,γ

(l m

, lm

)

+[n(n − 1)n

− 1)]

1/2

×[

n−1

n−2

n−1

n−2

n−1

n−2

−1

...γ

n−1

,γ

n−1

n−2

,γ

n−1

n−2

,γ

−1

,γ

×I

(l m

, lm

)

209

+{Γ

, Γ

n−1

} ↔ {Γ

, Γ

−1

}

– многоэлектронные интегралы переноса. Например, для s-зон мы получаем

H = U

(2, 2) +

{β

(00)

(σ, 0)X

(0, σ) + β

(22)

(2, σ)X

(σ, 2) (C.23)

+σβ

(02)

(σ, 0)X

(−σ, 2) + X

(2, −σ)X

(0, σ)

где U = I

νννν

= F

(0)

(00) – параметр Hubbard,

(00)

= β

(C.24)

(22)

= β

+ 2I

(02)

= β

(20)

= β

+ I

– интегралы переноса для дырок и двойных состояний, и интеграл рождения дырок

и двоек; в соответствии с (C.3),

= I

(0)

−

drϕ

(r)ϕ

ν1

(r) (C.25)

где I

(0)

вычисляются для атомных функций ϕ. Необходимо отметить что зависи-

мость интегралов переноса от атомных ME термов может быть более сложной если

мы используем при решении атомной проблемы подходы более сложные чем в При-

ложении A. Например, общее приближение Хартри-Фока (см. [20]) дает радиальные

одноэлектронные функции которые явно зависят от атомных термов. В некоторых

вариационных подходах многоэлектронной атомной теории (см. [664]) ME волно-

вые функции не факторизуются на одноэлектронные. Поэтому интегралы переноса

должны быть вычислены с использованием ME волновых функций:

(Γ

n−1

, Γ

−1

) =

∗

(C.26)

−

¯h

∆

+ V (r

)

В частности, для s - зон интегралы (C.24) могут отличаться даже в пренебреже-

нии межатомным кулоновским взаимодействием и неортогональности. Кроме этого,

может потребоваться многоэлектронный подход, который принимает во внимание

взаимодействие различных электронных оболочек.

Чтобы проанализировать m-зависимость двухузельных матричных элементов,

удобно преобразовать их в одноузельные разлагая волновые функции ϕ

(r) вблизи

первого атома [665]. Переходя к Fourier образам

(r) =

dke

ikr

(k)Y

(

k) (C.27)

(где

(k) – фурье-образ радиальной функции) и разлагая плоские волны по сфери-

ческим гармоникам

ikr

= 4π

λµ

(kr)Y

∗

λµ

(

k)Y

(ˆr) (C.28)

210

Ирхин В.Ю., Ирхин Ю.П. Электронная структура, корреляционные эффекты и физические свойства d - и f-переходных металлов и их соединений

Подождите немного. Документ загружается.