Ирхин В.Ю., Ирхин Ю.П. Электронная структура, корреляционные эффекты и физические свойства d - и f-переходных металлов и их соединений
Подождите немного. Документ загружается.


H
int
= −I
X
iσσ
0
(S
i
σ
σσ
0
)c
†
iσ
c
iσ
0
где S
q
- операторы локализованных спинов, σ - матрицы Паули, I - параметр s-d(f) об-
менного взаимодействия, которое предполагается контактным (вывод s-d(f) модели
в более общем случае рассматривается в Приложении K), J
q
- Фурье компоненты об-
менных параметров между локализованными спинами. В редкоземельных металлах
последнее взаимодействие обычно является косвенным РККИ обменом через элек-
троны проводимости, причиной которого является то же самое s-f взаимодействие.
Однако при построении теории возмущений удобно включить это взаимодействие в
нулевой гамильтониан.
Имея более сложную форму, s-d модель оказывается в некотором отношении бо-
лее простой, чем модель Хаббарда, так как в этой модели возможно выполнить
квазиклассическое разложение по малому параметру 1/2S. При использовании про-
стых аппроксимаций, результаты s-d(f) модели и модели Хаббарда отличаются как
правило только заменой I → U.
Ниже будет проделано систематическое исследование спин-волновых и электрон-
ных спектров проводящих ферро- и антиферромагнетиков в рамках вышеупомя-
нутых моделей. Будут продемонстрированы сходства и различия по сравнению с
магнитными изоляторами, которые обладают локализованными моментами и опи-
сываются моделью Гейзенберга.
G.1 Ферромагнетики
Следуя главным образом статье [338], рассмотрим здесь спин-волновую теорию хаб-
бардовских ферромагнетиков. Мы используем в качестве приближение нулевого по-
рядка спин-расщепленные стонеровские состояния. (Предел сильных корреляций об-
суждается в п.4.6 и Приложениях H, J.) Простейшее приближение Хартри-Фока
(Стонера) в модели Хаббарда, которое формально соответствует теории возмуще-
ний первого порядка по U, дает электронный спектр следующего вида
E
kσ
= t
k
+ Un
−σ
= t
k
+ U(
n
2
− σhS
z
i) ≡ t
kσ
(G.3)
так что имеем для спинового расщепления
∆ = U(n
↑
− n
↓
) = 2UhS
z
i (G.4)
и U играет роль параметра Стонера. Расцепление Хартри-Фока не учитывает кор-
ректно формирования "двоек", то есть дважды занятых состояний на узле. (Это
может быть сделано с использованием многоэлектронного приближения Хаббарда
[28-31], см. Приложение H). Следует обратить внимание, что этот недостатоу не иг-
рает роли для насыщенного ферромагнитного состояния.
В отличие от теории Стонера, модель Хаббарда позволяет описывать спин-
волновые возбуждения в коллективизированном ферромагнетике. Представим Га-
мильтониан взаимодействия в следующем виде
H
int
=
U
2
X
kσ
c
†
kσ
c
kσ
−
U
2
X
q
(S
−
−q
S
+
q
+ S
+
q
S
−
−q
) (G.5)
231

где вводятся фурье-компоненты операторов спиновой плотности
S
+
q
=
X
k
c
†
k↑
c
k+q↓
, S
−
q
=
X
k
c
†
k↓
c
k+q↑
(G.6)
S
z
q
=
1
2
X
k
(c
†
k↑
c
k+q↑
− c
†
k↓
c
k+q↓
)
Первый член в (G.5) дает перенормировку химического потенциала и может быть
опущен. Рассмотрим спиновую функцию Грина
G
q
(ω) = hhS
+
q
|S
−
−q
ii
ω
Записывая цепочку уравнений движения для нее, получаем
G
q
(ω) = 2hS
z
i +
X
k
(t
k+q
− t
k
)hhc
†
k↑
c
k+q↓
|S
−
−q
ii
ω
(G.7)
(ω − t
k+q
+ t
k
− ∆)hhc
†
k↑
c
k+q↓
|S
−
−q
ii
ω
= (n
k↑
− n
k+q↓
)[1 − UG
q
(ω)] (G.8)
где введена неприводимая функция Грина
L
kqp
= δhhc
†
k↑
S
+
p
c
k+q−p↑
− c
†
k+p↓
S
+
p
c
k+q↓
−δ
pq
(n
k↑
− n
k+q↓
)S
+
q
|S
−
−q
ii
ω
(G.9)
(cимвол δ означает, что хартри-фоковские расцепления должны быть исключе-
ны).Подставляя (G.8) в (G.7) получаем
G
q
(ω) =
hS
z
i − Ω
q
(ω)/U
ω − Ω
q
(ω) − π
q
(ω)
(G.10)
Ω
q
(ω) = U
X
k
t
k+q
− t
k
t
k+q
− t
k
+ ∆ − ω
(n
k↑
− n
k+q↓
) (G.11)
где поляризационный оператор π определяется функцией Грина (G.9). Пренебрегая
функцией π, получаем приближение случайных фаз (RPA). В отличие от стандарт-
ного вида
G
q
(ω) =
Π
q
(ω)
1 − UΠ
q
(ω)
(G.12)
где
Π
q
(ω) =
X
k
n
k↑
− n
k+q↓
ω + t
k↑
− t
k+q↓
представление (G.10) явно дает магнонный (спин-волновой) полюс
ω
q
' Ω
q
(0) =
X
kσ
A
σ
kq
n
kσ
(G.13)
причем
A
σ
kq
= σU
t
k+q
− t
k
t
k+q
− t
k
+ σ∆
(G.14)
232

имеет смысл амплитуды электрон-магнонного взаимодействия. При разложении по
q получаем
ω
q
= D
αβ
q
α
q
β
где
D
αβ
=
U
∆
X
k
·
∂
2
t
k
∂k
α
∂k
β
(n
k↑
+ n
k↓
) −
1
∆
∂t
k
∂k
α
∂t
k
∂k
β
(n
k↑
− n
k↓
)
¸
(G.15)
компоненты тензора спин-волновой жесткости. В случае слабого ферромагнетика
(∆ ¿ E
F
, U) получаем
D
αβ
=
U∆
4
X
k
·
∂
2
t
k
∂k
α
∂k
β
∂
2
n
k
∂t
2
k
+
1
6
∂t
k
∂k
α
∂t
k
∂k
β
∂
3
n
k
∂t
3
k
¸
(G.16)
так что D ∼ ∆. Магнонное затухание в RPA имеет следующий вид
γ
(1)
q
(ω) = −Im Ω
q
(ω) = πU∆ω
X
k
µ
−
∂n
k↑
∂t
k↑
¶
δ(ω − t
k+q↓
+ t
k↑
) (G.17)
γ
(1)
q
≡ γ
(1)
q
(ω
q
) ' πU∆ω
q
N
↑
(E
F
)N
↓
(E
F
)θ(ω
q
− ω
−
) (G.18)
где θ(x) - ступенчатая функция. ω
−
= ω(q
0
) есть пороговая энергия, которая опре-
деляется условием вхождения в стонеровский континуум (распад стонеровских воз-
буждений, то есть электронно-дырочных пар), q
0
является минимальным (по k) ре-
шением уравнения
t
k+q
0
↓
= t
k↑
= E
F
(G.19)
Величина ω
−
определяет характерный энергетический масштаб, разделяющий две
температурных области: вклады от спиновых волн (полюсы функции Грина (G.10))
преобладают при T < ω
−
, а вклады от возбуждений Стонера (разреза) при T > ω
−
.
В случае слабых ферромагнетиков вклад разреза в спиновую функцию Грина
можно приближенно рассматривать как парамагнонный полюс с комплексным ω, и
таким образом получаем
q
0
= k
F ↑
− k
F ↓
, ω
−
= D(k
F ↑
− k
F ↓
)
2
∼ ∆
3
∼ T
2
c
/E
F
(G.20)
Так как q
0
мало, при малых q > q
0
вместо (G.18) получаем
γ
(1)
q
(ω
q
) '
U∆ω
q
v
0
4π
(m
∗
)
2
≡ A/q (G.21)
Оценка (G.20) справедлива также для s-d(f) обменной модели с косвенным РККИ-
взаимодействием, для которого
D ∼ T
c
/S ∼ I
2
S/E
F
(G.22)
Затухание при очень малых q < q
0
(когда (G.17) исчезает) возникает из-за двух-
магнонных процессов рассеивания. Чтобы рассмотреть их, необходимо вычислить
233

функцию π в ведущем порядке по флуктуационной части кулоновского взаимодей-
ствия. Записывая уравнение движения для функции Грина (G.9), получаем
Π
q
(ω) =
X
pk
(A
↑
kq
)
2
[B(k ↑, k + q − p ↑,ω
p
− ω) + B(k + p ↓, k + q ↓,ω
p
− ω)
−B(k + p↓,k ↑ ,ω
p
) − B(k + q ↓, k + q − p ↓,ω
p
)] (G.23)
где
B(k
0
σ
0
, kσ, ω) =
N
p
(n
k
0
σ
0
− n
kσ
) + n
k
0
σ
0
(1 − n
kσ
)
ω − t
k
0
σ
0
+ t
kσ
Требуемое магнонное затухание дается мнимой частью (G.23). После некоторых пре-
образований получаем
γ
(2)
q
(ω) = π
X
kpσ
(A
↑
kq
)
2
(n
kσ
− n
k+q−pσ
) [N
p
− N
B
(ω
p
− ω)]
×δ(ω + t
k
− t
k+q−p
− ω
p
) (G.24)
Интегрирование для изотропного электронного спектра дает [682,683]
γ
(2)
q
(ω) =
v
2
0
12π
3
q
4
4hS
z
i
2
X
σ
k
2
F σ
×
½
ω
q
/35 , T ¿ ω
q
(T/4)
¡
ln(T/ω
q
) +
5
3
¢
, T À ω
q
(G.25)
Вещественная часть (G.23) описывает температурную зависимость спиновой жест-
кости, появляющуюся вследствие двухмагнонных процессов (кроме простейшего T
2
-
вклада, который появляется из температурной зависимости функций распределения
Ферми в (G.10)). Спин-волновой вклад связан с магнонными функциями распреде-
ления и пропорционален T. Более интересен неаналитический многоэлектронный
вклад, обусловленный функциями Ферми:
δD
αβ
=
1
4hS
z
i
2
X
pk
∂t
k
∂k
α
∂t
k
∂k
β
·
n
k↓
(1 − n
k−p↑
)
t
k
− t
k−p
− ω
p
+ (G.26)
+
n
k+p↓
(1 − n
k↓
)
t
k+p
− t
k
− ω
p
−
n
k+p↓
(1 − n
k↑
)
t
k+p↓
− t
k↑
− ω
p
−
n
k↓
(1 − n
k−p↓
)
t
k↓
− t
k−p↑
− ω
p
¸
Выполняя интегрирование для параболических спектров электронов и магнонов
(t
k
= k
2
/2m
∗
, ω
q
= Dq
2
), получаем
δD(T ) =
µ
πv
0
T
12hS
z
im
∗
¶
2
1
D
"
X
σ
N
2
σ
(E
F
) ln
T
ω
+
− 2N
↑
(E
F
)N
↓
(E
F
) ln
max(ω
−
, T )
ω
+
¸
(G.27)
где
ω
±
= D(k
F ↑
± k
F ↓
)
2
, N
σ
(E
F
) = m
∗
v
0
k
F
/2π
2
(G.28)
234

При ω
−
¿ T ¿ ω
+
мы получаем
δD(T ) =
µ
πv
0
T
12hS
z
im
∗
¶
2
1
D
[N
↑
(E
F
) − N
↓
(E
F
)]
2
ln
T
ω
+
(G.29)
Следует отметить, что поправки (G.27) преобладают при низких температурах над
вышеупомянутыми T
2
-членами, что демонстрирует важную роль поправок к RPA
приближению. К сожалению, член T
2
ln T еще не рассматривался при анализе спек-
тра магнонов в ферромагнитных металлах. Видно, что температурные зависимости
спин-волновых характеристик в проводящих магнетиках значительно отличаются от
поведения в модели Гейзенберга.
Чтобы получить поправки к приближению Стонера для электронного спектра
(G.3), необходимо вычислить одноэлектронную функцию Грина
G
kσ
(E) = hhc
kσ
|c
†
kσ
ii
E
= [E − t
kσ
− Σ
kσ
(E)]
−1
(G.30)
Для собственно-энергетической части получаем [573]
Σ
kσ
(E) = U
2
X
q
Z
∞
−∞
dω
π
ImhhS
σ
q
|S
−σ
−q
ii
ω
N
B
(ω) + n
k+q,−σ
E − t
k+q,−σ
+ ω
(G.31)
Сохраняя только вклад магнонных полюсов в спектральную плотность (то есть пре-
небрегая затуханием спиновых волн), можно записать
−
1
π
ImhhS
σ
q
|S
−σ
−q
ii
ω
= 2σhS
z
iδ(ω − σω
q
) (G.32)
так что
hS
−
−q
S
+
q
i = 2hS
z
iN
p
(G.33)
Тогда получаем
Σ
k↑
(E) = U∆
X
q
N
q
+ n
k+q↓
E − t
k+q↓
+ ω
q
Σ
k↓
(E) = U∆
X
q
1 + N
q
− n
k−q↑
E − t
k−q↑
− ω
q
(G.34)
Результаты (G.34) справедливы в s-d модели (U → I) в первом порядке по малому
параметру 1/2S [323]. Принимая во внимание соотношение
hS
z
i = S
0
−
X
p
N
p
(G.35)
где S
0
- намагниченность насыщения, получаем для спин-волновых поправок к энер-
гии электрона
δE
kσ
(T ) =
X
q
A
σ
kq
N
q
(G.36)
=
v
0
2hS
z
i
ξ(5/2)
32π
3/2
µ
T
D
¶
5/2
"
∂
2
t
k
∂k
2
x
−
σ
UhS
z
i
µ
∂t
k
∂k
¶
2
#
235

Зависимость электронного спектра T
5/2
, обусловленная магнонами, более слаба, чем
зависимость намагниченности T
3/2
. Этот факт связан с обращением в нуль амплиту-
ды электрон-магнонного взаимодействия A при нулевом волновом векторе магнона,
что связано с симметрией обменного взаимодействия. Подобное ослабление темпе-
ратурной зависимости спинового расщепления наблюдалось в железе [145]. Следует
отметить, что зависимость T
5/2
также имеет место в ферромагнетике с хаббардов-
скими подзонами [337,338].
Одноэлектронные числа заполнения получаются через спектральное представле-
ние для антикоммутаторной функции Грина (G.30):
hc
†
k↑
c
k↑
i = f(t
k
+ Re Σ
k↑
(t
k↑
)) (G.37)
+U∆
X
p
N
p
(n
k+p↓
− n
k↑
) + n
k+p↓
(1 − n
k↑
)
(t
k+p↓
− t
k↑
− ω
p
)
2
hc
†
k↓
c
k↓
i = f(t
k
+ Re Σ
k↓
(t
k↓
)) (G.38)
+U∆
X
p
N
p
(n
k↓
− n
k−p↑
) + n
k↓
(1 − n
k−p↑
)
(t
k−p↑
− t
k↓
+ ω
p
)
2
где второй член происходит от мнимой части собственной энергии. Сохраняя только
магнонные вклады до T
3/2
, получаем
hc
†
kσ
c
kσ
i ' n
kσ
S
0
+ hS
z
i
2S
0
+ n
k−σ
S
0
− hS
z
i
2S
0
(G.39)
где hS
z
i определяется из (G.35). Таким образом, несмотря на присутствие спинового
расщепления, электронные числа заполнения имеют сильную зависимость T
3/2
, а
не экспоненциальную зависимость (как в теории Стонера). Эта зависимость возни-
кает из-за процессов испускания и поглощения тепловых магнонов. Таким образом
спиновая поляризация электронов проводимости
P =
n
↑
− n
↓
n
↑
+ n
↓
(G.40)
равняется относительной намагниченности, что очевидно для коллективизирован-
ных ферромагнетика. Однако такое поведение имеет место также для произвольных
проводящих ферромагнетиков, например, для ферромагнитных полупроводников,
которые описываются s-d(f) обменной моделью [329]. Формально, T
3/2
- зависимость
P(T) имеет место из-за сильной температурной зависимости вычетов электронных
функций Грина и появления неквазичастичных состояний в "чужой"спиновой под-
зоне вследствие электрон-магнонного рассеивания. Картина плотности состояний
обсуждается более детально в п.4.5.
Рассмотрим поправки к намагниченности hS
z
i. Имеем
hS
z
i =
n
2
−
X
q
hS
−
q
S
+
q
i − hbn
i↑
bn
i↓
i (G.41)
Первое среднее, входящее в (G.41), рассчитывается из спектрального представления
функции Грина RPA (G.10):
hS
−
−q
S
+
q
i = 2S
0
N
q
(q < q
0
) (G .42)
236
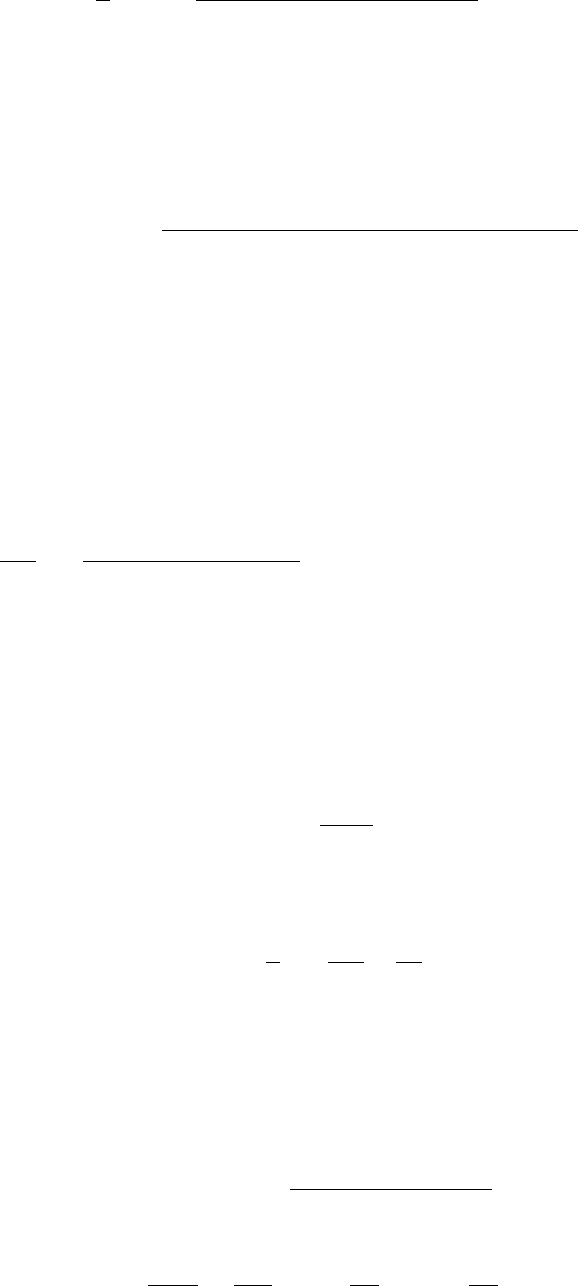
hS
−
−q
S
+
q
i =
1
π
Z
∞
−∞
dω
N
B
(ω)γ
(1)
q
(ω)(∆ − ω)/U
[ω − Re Ω
q
(ω)]
2
+ [γ
(1)
q
(ω)]
2
(q > q
0
) (G.43)
Используя соотношение
N
B
(t
k+q↓
− t
k↑
)(n
k↑
− n
k+q↓
) = n
k+q↓
(1 − n
k↑
) (G.44)
мы получаем из (G.43)
hS
−
−q
S
+
q
i =
X
k
(t
k+q↓
− t
k↑
)
2
n
k+q↓
(1 − n
k↑
)
(t
k+q↓
− t
k↑
− ω
q
)
2
+
h
γ
(1)
q
(t
k+q↓
− t
k↑
)
i
2
(G.45)
В отличие от (G.41), (G.42), истинный блоховский спин-волновой вклад в намагни-
ченность должен даваться (G.35), так как каждый магнон уменьшает hS
z
i на едини-
цу. Согласие может быть восстановлено, если учесть не только магнонный полюс, но
и вклад от разреза. Заменяя в (G.45) n
kσ
→ hc
†
kσ
c
kσ
i и используя (G.39), получаем
δhS
z
i
SW
= −
X
q
N
q
[2S
0
+ (G.46)
+
1
2S
0
X
kk
0
(t
k
− t
k
0
)
2
(n
k↑
− n
k↓
)
(t
k
0
↓
− t
k↑
− ω
k−k
0
)
2
(1 − n
k
0
↑
+ n
k
0
↓
)
#
' −
X
q
N
q
где мы пренебрегаем спиновым расщеплением в знаменателе.
Полуфеноменологически удобно ввести "магнонные"операторы, которые удовле-
творяют в среднем коммутационным соотношениям Бозе:
b
q
= (2S
0
)
−1/2
S
+
q
, b
†
q
= (2S
0
)
−1/2
S
−
−q
(G.47)
Тогда получаем
δhS
z
i = −
X
q
hb
†
q
b
q
i =
1
(2S
0
)
X
q
hS
−
−q
S
+
q
i (G.48)
Выполняя интегрирование по ω в (G.43) при T = 0, получаем
δhS
z
i = −
1
π
X
q
γ
(1)
q
ω
q
ln
W
ω
q
(G.49)
где W - ширина зоны. Этот вклад описывает уменьшение намагниченности из-за
затухания магнонов в основном состоянии, проявляющееся из-за возбуждений Сто-
нера. Для параболического электронного и магнонного спектров, пренебрегая зату-
ханием в знаменателе (G.43), получаем при низких температурах T < ω
−
δhS
z
i
cl
' −U∆
X
kk
0
n
k
0
↓
(1 − n
k↑
)
(t
k
0
↓
− t
k↑
− ω
k−k
0
)
2
= −
µ
m
∗
v
0
2π
2
¶
2
U∆
4D
·
ω
+
ln
W
ω
+
− ω
−
ln
W
ω
−
237

+
2π
2
3
T
2
µ
1
ω
−
−
1
ω
+
¶¸
(G.50)
где ω
±
определена в (G.28). Для слабого ферромагнетика, температурная поправка к
hS
z
i в (G.50) пропорциональна (T/T
C
)
2
, что находится в согласии с самосогласован-
ной перенормированной теорией [296,26]. Следует обратить внимание, что получен-
ная T
2
-поправка является намного большей, чем вклад Стонера порядка (T/E
F
)
2
.
Учет затухания при низких T влияет только на числовые коэффициенты в (G.50).
В то же самое время, при высоких T > ω
−
затухание в знаменателе преобладает при
малых q в случае слабого ферромагнетика. Принимая во внимание (G.21), получаем
из (G.43)
δhS
−
−q
S
+
q
i =
∆
πU
Z
∞
−∞
dωN
B
(ω)
Z
∞
0
ωAqdq
(Dq
2
)
2
+ A
2
ω
2
/q
2
∼
µ
T
E
F
¶
4/3
(G.51)
Таким образом, мы получаем из (G.41) поправку к намагниченности вида T
4/3
, что
совпадает с результатом скейлинговой теории фазовых переходов вблизи T = T
C
.
Для ферромагнетика с хорошо локализованными магнитными моментами затухани-
ем можно пренебречь, и мы получаем [716]
δhS
z
i
el
∼ −I
2
ω
−
ln(T/ω
−
) (G.52)
Рассмотрим перенормировку электронной теплоемкости в коллективизирован-
ном ферромагнетике из-за взаимодействия со спиновыми флуктуациями. Интегри-
рование в (G.34) при T=0 дает
Re Σ
σ
(k
F σ
, E) = −
U∆
ω
+
− ω
−
N
−σ
(E
F
)
X
α=±
α(E − ω
α
) ln
|E − ω
α
|
W
(G.53)
Тогда обратный вычет электронной функции Грина
Z
−1
kσ
(E) = 1 −
∂
∂E
Re Σ
kσ
(E)
принимает форму
Z
−1
σ
(k
F σ
, E
F
) = 1 +
U∆
ω
+
− ω
−
N
−σ
(E
F
) ln
¯
¯
¯
¯
E − ω
+
E − ω
−
¯
¯
¯
¯
(G.54)
Величина (G.54) определяет перенормировку электронной эффективной массы из-за
электрон-магнонного взаимодействия. Таким образом, для коэффициента при ли-
нейном члене в электронной теплоемкости (T ¿ ω
−
) получаем
γ
σ
= γ
(0)
σ
/Z
σ
(k
F σ
, E
F
) =
π
2
3
N
σ
(E
F
) [1+
+
U∆
ω
+
− ω
−
N
−σ
(E
F
) ln
ω
+
ω
−
¸
(G.55)
Для слабых коллекитвизированных ферромагнетиков имеем
ln
ω
+
ω
−
' −2 ln(UN(E
F
) − 1) (G.56)
238
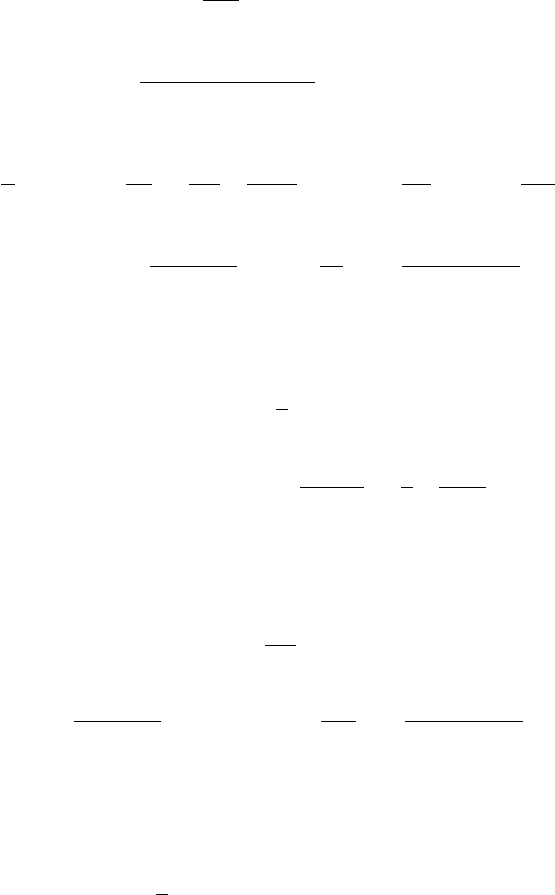
так что выражение (G.55) описывает парамагнонное увеличение теплоемкости
[297,573] обсуждаемое в п.4.4. Численный коэффициент в (G.55) неточен в этом
пределе из-за пренебрежения продольными спиновыми флуктуациями (см.[26]). С
другой стороны, наше рассмотрение не ограничивается случаем слабых ферромаг-
нетиков. Это важно, поскольку значительное повышение удельной теплоты из-за
спиновых флуктуаций наблюдается во множестве сильных ферромагнетиков. На-
пример, экспериментальное значение γ в системе CeFe
1−x
Co
x
S
2
(где при увеличении
x происходит ферро-антиферро переход ) в ферромагнитной фазе γ = 48 мДж/моль
K
2
(x = 0), что превышает в два раза теоретическое значение, полученное из рас-
четной плотности состояний, и значительно больше, чем значения в пара- и анти-
ферромагнитных фазах [684].
Другие термодинамические свойства могут быть исследованы при вычислении
свободной энергии системы. При низких T < ω
−
многоэлектронный вклад от разреза
имеет вид
F
el
=
1
2S
0
X
q>q
0
ω
q
hS
−
−q
S
+
q
i (G.57)
' U∆
X
kk
0
n
k
0
↓
(1 − n
k↑
)
t
k↑
− t
k
0
↓
+ ω
k−k
0
≡ F
el
(0) + δF
el
(T )
где
F
el
(0) =
1
π
X
q
γ
(1)
q
ln
W
ω
q
≈
1
8D
µ
m
∗
v
0
2π
2
¶
2
·
ω
2
+
ln
W
ω
+
− ω
2
−
ln
W
ω−
¸
(G.58)
δF
el
(T ) = −
U∆
ω
+
− ω
−
N
↑
(E
F
)
π
2
3
T
2
ln
ω
+
max(ω
−
, T )
(G.59)
Спин-волновой вклад в свободную энергию имеет форму, обычную для бозе-
возбуждений с квадратичным законом дисперсии
δF
SW
= −
2
3
δhHi
SW
, (G.60)
δhH i
SW
=
X
q<q
0
ω
q
N
q
=
3v
0
16π
3/2
ξ
µ
5
2
¶
T
5/2
D
3/2
Зависящие от температуры поправки к физическим свойствам получаются из (G.59),
(G.60). Дифференцируя (G.59) по T , получаем
δC
el
= −
∂
∂T
δF
el
(T ) (G.61)
= U
2
2hS
z
i
ω
+
− ω
−
N
↑
(E
F
)N
↓
(E
F
)
2π
2
3
T ln
ω
+
max(ω
−
, T )
Таким образом, при T À ω
−
получаем вместо (G.55) зависимость теплоемкости вида
T ln T .
Рассмотрим локальный магнитный момент на узле
hS
z
i =
3
4
(n − 2N
2
), N
2
= hn
i↑
n
i↓
i (G.62)
239

Число двоек N
2
может быть определено с помощью теоремы Геллмана-Фейнмана
N
2
= ∂F/∂U. При T < ω
−
получаем
δhS
z
i
el
(T ) ∼ −(T/∆)
2
δhS
z
i
el
(T ) ∼ −(T/T
c
)
5/2
(G.63)
Таким образом, температурная зависимость спин-волнового вклада в hS
2
i более сла-
ба, чем температурная зависимость спин-волнового вклада в hS
z
i, что оправдыва-
ет пренебрежение им в обсуждении намагниченности, которое было сделано выше
(G.41). При высоких T локальный момент имеет следующую T-зависимость:
δhS
2
i
i = δ
X
q
hS
−
−q
S
+
q
i ∼ (T/E
F
)
4/3
(G.64)
Как видно из (G.55), усиление эффективной массы и электронной теплоемкости из-
за спиновых флуктуаций отсутствует в полуметаллическом состоянии (п.4.5). По-
кажем, что теплоемкость проводящего ферромагнетика может содержать вклады
спиновых флуктуаций другой природы. Запишем общее выражение для удельной
теплоты в s-d обменной модели через полную энергию
C(T ) =
∂hHi
∂T
=
∂
∂T
Z
dEEf(E)N
t
(E) (G.65)
=
π
2
3
N
t
(E)T +
Z
dEEf(E)
∂
∂T
N
t
(E, T )
где
N
t
(E) = −
1
π
X
kσ
Im G
kσ
(E)
есть полная плотность состояний. Первый член справа (G.65) дает стандартный ре-
зультат теории ферми-жидкости. Второй член появляется из-за энергетической за-
висимости плотности состояний. Такая зависимость появляется в проводящем фер-
ромагнетике из-за неквазичастичных (некогерентных) состояний (см. п.4.5). Под-
ставляя (4.87) в этот член, получаем [338]
δC
σ
(T ) = 2σI
2
hS
z
i
X
kq
f(t
k+q,−σ
− σω
q
)
(t
k+q,−σ
− t
k,σ
)
2
∂
∂T
n
k+q,−σ
(G.66)
При низких температурах
f(t
k+q,↓
− ω
q
) = 1, f(t
k+q,↑
− ω
q
) = 0 (G.67)
Таким образом, неквазичастичные состояния с σ =↓ не вносят вклад в линейную
теплоемкость, так как они пусты при T = 0. В полуметаллическом состоянии неква-
зичастичные вклады (G.66) с σ =↑ присутствуют только при I < 0 , и мы получаем
δC
↑
(T ) =
2π
2
3
I
2
hS
z
iN
↓
(E
F
)T
X
k
1
(t
k↑
− E
F
)
2
(G.67)
Чтобы избежать недоразумений, следует отметить, что присутствие таких вкладов
в теплоемкость означает неприменимость фермижидкостного описания только че-
рез динамические квазичастицы, которые определяются полюсами функций Грина.
240
