Houze Robert A., Jr. Cloud Dynamics

Подождите немного. Документ загружается.

2.8 Adjustment to Geostrophic and Gradient Balance

may be combined to yield the

wave

equation

+ n'. + N

w' = 0

tt zt

The

continuity equation is

(2.121)

(2.122)

can

be verified by substitution

that

(2.118), (2.121), and (2.122) have solutions of

the form

where

, , ' ....r

i(kx+ly+mz-vt)

U,V,W,,,

oc e

(2.123)

(2.125)

(2.124)

(

2 2 ) ( 2 )

2 2 k +1 2 m

+ m

+ 1

+ m

The

factor multiplying N2 is the cosine squared

ofthe

angle

the phase lines from

the vertical, while the multiplier

is the sine squared

that angle. In the case

hydrostatic motions (i.e., m

» k

+ F), (2.124) reduces to

(

z2)

= N

2.8

Adjustment

to Geostrophic

and

Gradient Balance

As noted in Sec. 2.2.1, the large-scale environment in which cloud systems are

embedded

is typically in a state

near-geostrophic balance. Any disruption of

this balance (for example by a cloud system) can lead to the excitation of inertio-

gravity waves, which

act

to readjust the pressure field to geostrophic balance. The

physical mechanism

the adjustment is well illustrated by the shallow-water

versions

(2.118), which

are

and

-gh~

fv'

(2.126)

-gh;

fu'

(2.127)

The

continuity equation, obtained by integrating (1.22)

over

the depth

the water

and applying

boundary

conditions similar to those leading to (2.101), is

(u~

v;)11

= 0 (2.128)

The

divergence equation obtained by taking a(2.126)/ax + a(2.127)/ay is

h;t

gll(h:XX

h;y)

fll"

= 0 (2.129)

When there is no Coriolis effect

= 0), this equation reduces to a two-dimen-

sional shallow-water equation [cf. (2.102)] with gravity-wave solutions

the form

h' oc ei(k.x+ly-vt)

(2.130)

50 2 Atmospheric Dynamics

with

j)2

ghW

+ [2). When f

=1=

0, the height-perturbation and perturbation

vorticity fields are related by (2.129). Under geostrophic conditions, the time

derivatives in (2.126)-(2.129) disappear, and (2.129) simply states that the vortic-

ity field is in geostrophic balance. When the initial state is not in geostrophic

balance (e.g., Fig. 2.1), (2.129) describes the approach to geostrophic balance.

However, to accomplish this description a further relation between

hi and

needed.

For

this, we turn to the equation for the vertical component of vorticity

obtained by taking

a(2.127)/ax - a(2.126)/ ay. The result is

= -

)

(2.131)

which is a linearized perturbation form of (2.59). This equation may be combined

with the continuity equation to obtain the conservation property

(2.132)

The quantity in parentheses is a linearized form of the

shallow-water potential

vorticity.

retains its initial value everywhere in the spatial domain. Because of

this behavior, the final velocity field, after adjustment to geostrophic balance, can

be found from (2.129). If at

t = 0 the fluid is motionless (u

= Vi = 0) but its depth

hi is distorted into the step-function configuration illustrated in Fig. 2.1, then,

according to (2.132), the potential vorticity at a later time

t is

h' h

- -

--=-

sgn(x)

I h h

(2.133)

(2.134)

where

0 and sgn(x) indicates "sign of

x."

Substituting the value of

given by

this relation into the last term of (2.129) yields

h;t

-gh(h~

+h;y)+

h' =

hosgn(x )

17777777777771}hO

---

-::~~-::~~-::~~~

fluid

;=0

x--+-

Figure 2.1 Surface of shallow-water fluid distorted into a stair-step configuration. Notation is that

used in the text. The infinite horizontal pressure gradient, which must apply across the discontinuity, is

incompatible with a state of hydrostatic balance.

2.8 Adjustment to Geostrophic and Gradient Balance

If the surface is undisturbed (h; = 0), (2.134) has shallow-water, inertio-gravity

wave solutions of the form (2.130) with

gh(k

zZ)

(2.135)

which is the shallow-water version of (2.125).

For

a finite disturbance of the

surface

(h;

> 0), the final steady-state form of (2.134) is

2h'

h' h

---+-

_---.£...

sgn(x) (2.136)

where we have introduced the Rossby radius

deformation ,33 defined as

jfI-

(2.137)

(2.138)

The y-derivatives disappear from (2.136) because the perturbation is independent

y. The solution of (2.136) is

h'-h

{-l+eXP(-X/A

) ,

.e s o

- 0

l-exp(+x/A

) ,

x<O

(2.139)u' = 0,

Substitution of (2.138) into (2.126) and (2.127) show that the final perturbation

wind field is geostrophic (and nondivergent) with values

( )

v' =

exp -ixi/A

fAR

This flow is illustrated in Fig. 2.2.

has adjusted to a point where the Coriolis

force is

just

balanced by the pressure gradient force, and no further.

there were

no Coriolis effect, then geostrophic balance would never be achieved and gravity

waves would carry off all the potential energy of the initial perturbation. The final

pressure gradient would be flat, and the final values of

and Vi would be zero.

However, with the Coriolis effect present, the initial pressure gradient (mani-

fested by the step-like jump in the depth of the fluid) would not be wiped out

altogether by the gravity waves but rather would be spread over a finite distance of

e-folding width

2AR' This more gentle gradient of hi is in geostrophic balance.

Thus, some of the potential energy of the initial disturbance is retained as geo-

strophic perturbation kinetic energy (since

c:f=

0 in the final steady state).

turns

out that in this example one-third of the potential energy of the initial disturbance

goes into the steady geostrophic flow, while the remaining two-thirds is carried off

by the inertio-gravity waves.

A process analogous to geostrophic adjustment occurs in a strong circular flow,

such as a hurricane. If we again assume shallow-water flow but assume the basic

state is an axially symmetric circular vortex in gradient balance, with a mean

JJ Named for the Swedish-American meteorologist Carl-Gustav Rossby (1898-1957). Many of the

basic principles of modem atmospheric dynamics were first elucidated by him.

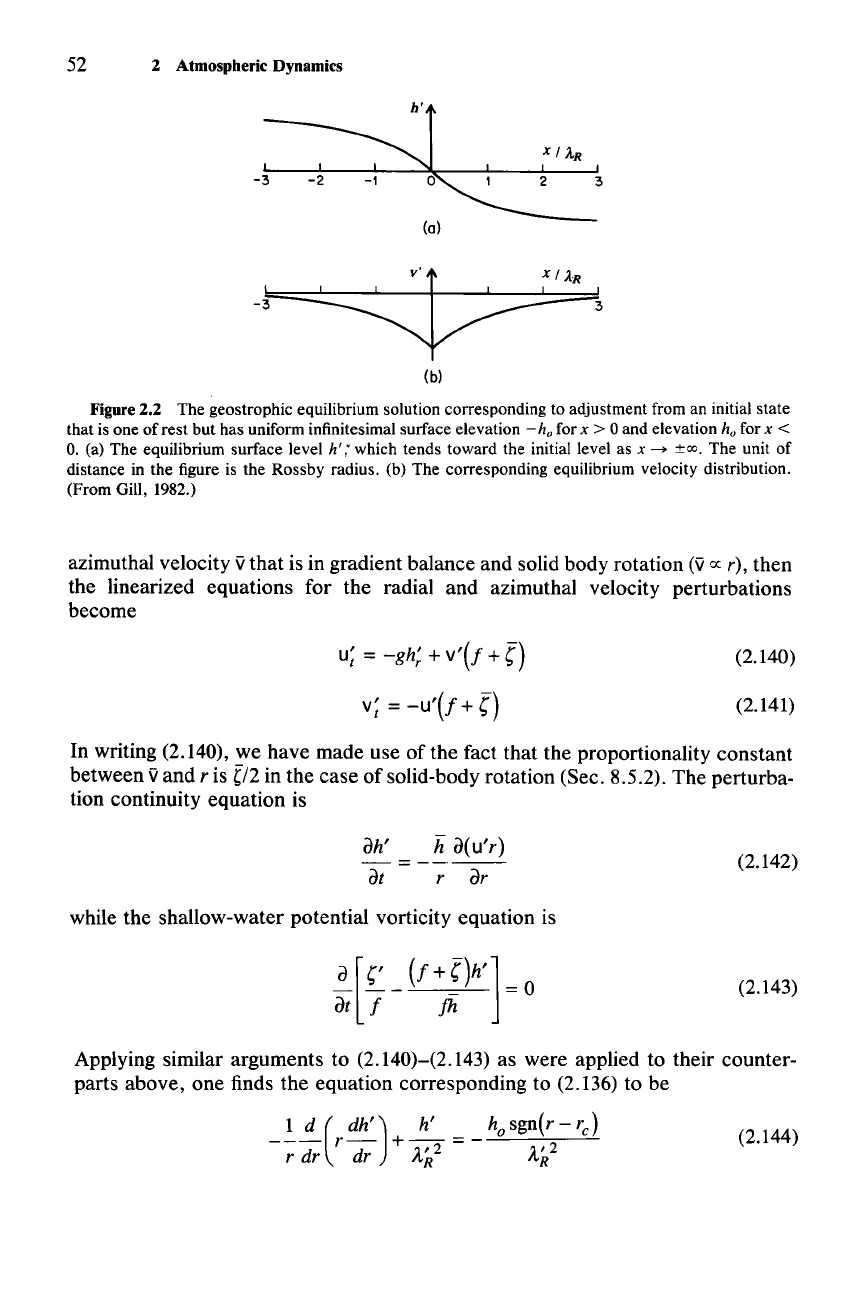
52 2 Atmospheric Dynamics

-3

(b)

Figure 2.2 The geostrophic equilibrium solution corresponding to adjustment from an initial state

that is one of rest but has uniform infinitesimal surface elevation -

h; for x > 0 and elevation h; for x <

(a) The equilibrium surface level

h';

which tends toward the initial level as x

±oo. The unit of

distance in the figure is the Rossby radius. (b) The corresponding equilibrium velocity distribution.

(From Gill, 1982.)

azimuthal velocity vthat is in gradient balance and solid body rotation

oc r), then

the linearized equations for the radial and azimuthal velocity perturbations

become

-gh;

v'(J

-u'(J

+ n

(2.140)

(2.141)

In writing (2.140), we have made use of the fact that the proportionality constant

between

vand r is (,/2 in the case of solid-body rotation (Sec. 8.5.2). The perturba-

tion continuity equation is

a(u'r)

----

while the shallow-water potential vorticity equation is

(2.142)

(2.143)

(2.144)

Applying similar arguments to (2.140)-(2.143) as were applied to their counter-

parts above, one finds the equation corresponding to (2.136) to be

-~~(r

dh')

= _ h

sgn(:

r dr dr

A;/

2.9 Instabilities 53

where r. is the radius of

ajump

in hi at the initial time, similar to that at x = 0 in

Fig. 2.1, and

(2.145)

which is the Rossby radius of deformation for the specified circular flow. The

Rossby radius in this case is influenced by the relative vorticity of the vortex as

well as by the

earth's

vorticityf. In a strong vortex (like a hurricane), the relative

vorticity dominates. When the radius of curvature of the basic flow vortex is

infinite (i.e., when the flow is straight)

reduces to AR.

2.9 Instabilities

2.9.1 Buoyant, Inertial, and Symmetric Instabilities

In Sees, 2.7 and 2.8 we have summarized some of the types of atmospheric

motions relevant to cloud dynamics. However, we have considered only those

situations for which

ao/

> 0, where 0is the potential temperature of a hydrostat-

ically balanced mean state, and

aM/ax>

0, where Mis the absolute momentum of

a two-dimensional geostrophically balanced mean state. Referring to (2.97) and

(2.117), we see that these are the cases for which, according to parcel theory, the

buoyancy and Coriolis restoring forces produce stable sinusoidal oscillations

about a parcel's initial equilibrium position. The oscillations are vertical in the

case of (2.97) and horizontal in the case of (2.117). Now we investigate briefly the

situations in which

ao/az

< 0 and

aM/ax

According to (2.97) and (2.117), the

solutions to the basic equations no longer oscillate stably, but may grow exponen-

tially. The environments in these situations are said to be unstable. Negative

thermal stratification

(ao/az

< 0) is called buoyant instability. Negative horizontal

shear

(aM/ax

< 0) is called inertial instability.

These two types of instability can be inferred heuristically by making the

parcel-theory assumption

(p*

= 0) and using the fact that

()

is conserved under

adiabatic conditions [according to (2.9)] and

M is conserved under two-dimen-

sional, inviscid conditions [according to (2.112)]. If a parcel of dry air is displaced

upward in a buoyantly unstable environment, it immediately becomes buoyant

and accelerates upward, according to (2.93). If a parcel of air is displaced in the

positive x-direction in an inertially unstable environment, it immediately obtains

an excess of absolute momentum

- M > 0) and is accelerated in the positive

x-direction, according to (2.111). In both cases, the displacement leads to the

parcel being accelerated in the direction of the displacement (i.e., away from the

equilibrium position).

Actually, the atmosphere is rarely unstable to dry-adiabatic displacements.

Pure buoyant instability is generally eliminated as rapidly as it builds up, since it is

released by any perturbation, no matter how small. However, as a result of the

54 2 Atmospheric Dynamics

conservation of

(Je

expressed by (2.18), there exists an analog to buoyant instabil-

ity that is relevant to motions within clouds.

a parcel of air in a saturated

environment (mean state) is displaced vertically upward, the parcel, which con-

serves its value of

(J"

will become positively buoyant if

aoe/az

A saturated

environment is thus buoyantly unstable in the same way that a dry atmosphere is

unstable when

ao/az

However, this type of instability is also quickly elimi-

nated and also rather rare.

Since the atmosphere is usually moist (i.e., contains water vapor) but

unsatu-

rated,

a situation called conditional instability can arise. A necessary condition

for this instability to exist is for the temperature in the undisturbed atmosphere to

decrease with height less rapidly than a dry parcel of air, conserving its

but more

rapidly than that of a saturated parcel conserving its

(Je'

In such an atmosphere, a

mass of moist but unsaturated air lifted under parcel-theory conditions above its

saturation level may eventually become warmer than the undisturbed environ-

ment. Nearly all convective clouds (cumulus and cumulonimbus) form in condi-

tionally unstable environments

and

acquire their buoyancy in this manner.

Another way to state the necessary condition for conditional instability is that

we must have

aoes/az

< 0, where

(Jes

is the saturation equivalent potential temper-

ature defined by

8(T,p)eLqvs(T,P)/C

T (2.146)

That is, the environment is conditionally unstable if the equivalent potential tem-

perature computed as if the environment were saturated decreases with height.

If a whole layer of air, which is initially moist but unsaturated and character-

ized by

aoe/az

< 0, is brought to saturation (e.g., by lifting), the whole layer

becomes buoyantly unstable. Such a layer of air is said to be

potentially unstable.

Severe thunderstorm occurrences are often preceded by a period in which a layer

of the atmosphere is potentially unstable. The storms occur when the potentially

unstable layer is lifted to saturation.

In the atmosphere, buoyancy and Coriolis forces act simultaneously.

the

large-scale mean state is both geostrophically and hydrostatically balanced and if

there is no friction or heating, motions are two-dimensional in the

x-z plane, and

we continue to make the assumption that

p* = 0 on a parcel, then both (2.93) and

(2.111) apply. An absolute momentum excess or deficit of a parcel displaced from

equilibrium leads to an acceleration in the horizontal, while a deficit or excess in

potential temperature leads to an acceleration in the vertical. These accelerations

may be in either the stable or unstable sense.

is possible for the atmosphere to

be stable for purely vertical or purely horizontal displacements but nonetheless

unstable to sloping or slantwise displacements. Such an environment is said to be

symmetrically unstable and can lead to strong slantwise air motions.

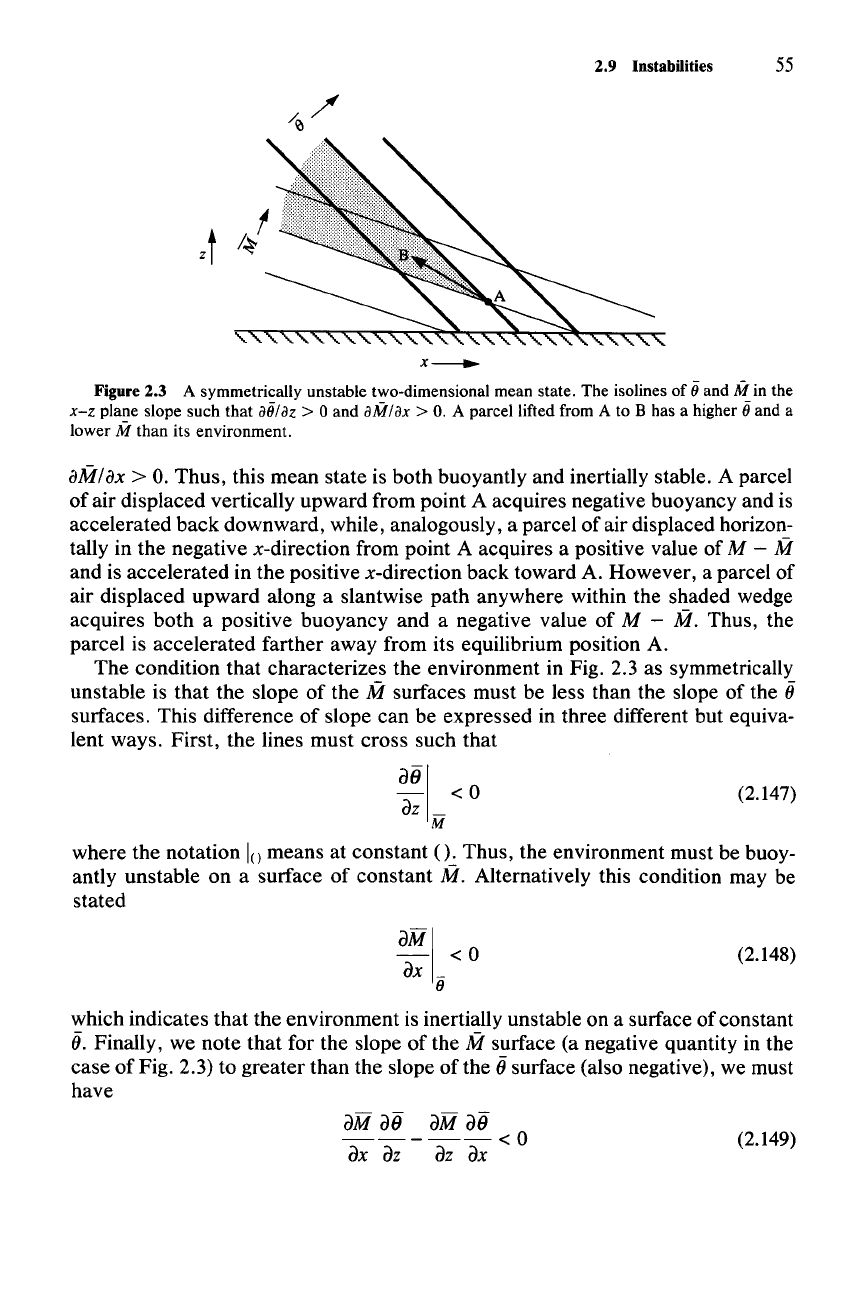
A symmetrically unstable two-dimensional mean state is illustrated in Fig. 2.3.

The isolines of

0 and M both slope in the x-z plane, but both

ao/

sz > 0 and

For

a more complete discussion of conditional and potential instability, see Wallace and Hobbs

(1977).

(2.147)

(2.148)

2.9 Instabilities 55

x-----.

Figure 2.3 A symmetrically unstable two-dimensional mean state. The isolines of jjand M in the

x-z

plane slope such that

ajj/az

> 0 and aM/ax>

A parcel lifted from A to B has a higher

and a

lower

M than its environment.

aM/ax>

Thus, this mean state is both buoyantly and inertially stable. A parcel

of air displaced vertically upward from point A acquires negative buoyancy and is

accelerated back downward, while, analogously, a parcel of air displaced horizon-

tally in the negative x-direction from point A acquires a positive value of

M - M

and is accelerated in the positive x-direction back toward A. However, a parcel of

air displaced upward along a slantwise path anywhere within the shaded wedge

acquires both a positive buoyancy and a negative value of

M - M. Thus, the

parcel is accelerated farther away from its equilibrium position A.

The condition that characterizes the environment in Fig. 2.3 as symmetrically

unstable is that the slope of the

M surfaces must be less than the slope of the ii

surfaces. This difference of slope can be expressed in three different but equiva-

lent ways. First, the lines must cross such that

alii

where the notation

means at constant O. Thus, the environment must be buoy-

antly unstable on a surface of constant

M. Alternatively this condition may be

stated

aMI

which indicates that the environment is inertially unstable on a surface of constant

ii.

Finally, we note that for the slope of the M surface (a negative quantity in the

case of Fig. 2.3) to greater than the slope of the

ii surface (also negative), we must

have

ali

-----<0

az az

(2.149)

56 2 Atmospheric Dynamics

However, from (2.66), this is equivalent to saying that the two-dimensional geo-

strophic mean state satisfies

< 0 (2.150)

(i.e., the mean state must have negative potential vorticity). Note that since

P is

conserved in adiabatic frictionless flow, fluid parcels cannot rid themselves of the

negative potential vorticity in the absence of heating and/or turbulent mixing.

If the air is saturated and parcels undergo adiabatic motion except for liquid-

vapor phase changes, so that (2.18) applies rather than (2.11), then the concept of

symmetric instability carries over if

0is replaced with

in (2.147)-(2.149), and P

is replaced with the geostrophic equivalent potential vorticity

Peg

in (2.150). If the

air is unsaturated, replacement of

0with

0;,

in (2.147)-(2.149), may be referred to

potential symmetric instability, which is analogous to the potential instability

described above; in other words, a layer in which

decreases with height on a

surface of constant

M would be potentially unstable for slantwise parcel displace-

ment,

the air were brought to saturation.

the air is moist, but unsaturated, a condition called conditional symmetric

instability

can also be identified, which is analogous to the conditional instability

described above. Conditional symmetric instability is said to exist when the tem-

perature lapse rate of a moist but unsaturated environment is conditionally unsta-

ble

on a surface

constant M (i.e., the slope of the M surfaces must be less than

the slope of the

Oes

surfaces). This condition is stated by replacing 0 by

Oes

(2.147)-(2.149). To illustrate, let us imagine the lines of

0in Fig. 2.3 to be replaced

by lines of

Oes'

the parcel at point A has already been lifted above its saturation

level and conserves

as it is displaced slantwise farther upward into the region of

the shaded wedge, then it will be positively buoyant at the same time that it is

subjected to inertial acceleration.

In a circular two-dimensional flow under gradient balance (Sec. 2.2.3), the

conserved momentum variable is the angular momentum

m rather than the abso-

lute momentum

M [cf. Eqs. (2.37) and (2.112)]. Hence, by analogy to (2.147)

and (2.148), the condition for symmetric instability in a two-dimensional gradient

flow is

ael

a-I

(}

(2.151)

Conditions for potential and conditional symmetric instability cast in terms of

follow by arguments analogous to those above.

2.9.2 Kelvin-Helmholtz Instability

In the previous section, we have seen that the vertical gradient of potential tem-

perature and the horizontal shear of the horizontal wind component are sources of

flow instability. Another source is the vertical shear of the horizontal wind. This

2.9 Instabilities 57

-..

Figure 2.4 Conceptual illustration of the growth of a sinusoidal disturbance to an initially uniform

sheet of vorticity (dashed) located between layers of fluid moving at different horizontal velocities

(UI

and

U2).

The local strength density of the sheet is represented by its thickness. The arrows indicate the

direction of the self-induced movement of the vorticity in the sheet and show both the accumulation of

vorticity at points like A and the general rotation about points like A, which together lead to

exponential growth of the disturbance. (From Batchelor, 1967.)

type of instability, referred to as Kelvin-Helmholtz instability P can be visualized

by the heuristic argument summarized in Fig. 2.4. Two fluids, one beneath the

other, are moving parallel to the x-axis, but at different speeds. When the system

is undisturbed, the interface of the two fluids is horizontal. The interface is re-

garded as a thin layer of strong vorticity, or "vortex sheet," which may be

thought of as consisting of a layer of small discrete vortices, all rotating in the

same direction. The up and down motions of the vortices cancel, while the hori-

zontal components reinforce and account for the net velocity difference from top

to bottom

the vortex sheet.

the sheet is perturbed sinusoidally (as shown), the

vortex elements interact to produce velocity perturbations along the sheet. The

vortex elements at A and C produce leftward motion in the region under wave

crest B and rightward motion above trough D. These motions advect the vortex

sheet in the direction of exaggerating the perturbation at A and weakening the one

at C. They concentrate vorticity at A and lessen its intensity at C. The stronger

counterclockwise rotation at A lifts the crest and lowers the trough, and the

fluid-

motion perturbations are amplified.

Kelvin-Helmholtz instability is related quantitatively to the differences of ve-

locity and density between the two fluids. The velocity difference is a measure of

the intensity of the vorticity, which is locally intensified by perturbations accord-

ing to Fig. 2.4. The greater the velocity difference, the stronger the instability. The

density difference is important because, the more the density of the lower fluid

exceeds that of the upper fluid, the greater the buoyant stability, and thus the

more the buckling of the interface will be suppressed by the buoyancy restoring

force. From Fig. 2.4, positive buoyancy exists above the troughs and negative

buoyancy below each crest. The vorticity associated with the velocity difference

across the interface must be strong enough for perturbations in the interface to

overcome these restoring forces.

35 Named after Lord Kelvin and Herman von Helmholtz, who first developed the mathematics of

this type of instability in the late nineteenth century. Further discussions of the topic can be found in

Lamb (1932), Turner (1973), Batchelor (1967), Lilly

(1986),

and Acheson

(1990).

58 2 Atmospheric Dynamics

Fluid 1

PI,UI

Undisturbed interface

(2.153)

(2.155)

Figure 2.5 Notation used to describe a sinusoidal disturbance to an initially uniform vorticity

sheet (dashed) located between layers of fluid of different densities

(PI and P2) moving at different

horizontal velocities

(UI and U2)'

The classical mathematical expression of the instability condition.t" which in-

cludes the relative amounts of. velocity shear and density difference across the

interface, can be obtained by considering a highly idealized case in which the two

fluids on either side of the interface are homogeneous and all vorticity in the

system is contained in an infinitesimally thin interface. We will first review the

analysis of this classical case, which indicates how waves form on the interface

and results in the instability conditions given in (2.163) and (2.164) below. Then

we will derive the instability condition (2.170), which applies to a continuously

stratified fluid.

The classical case is obtained by considering the situation depicted in Fig. 2.5.

The upper fluid is indicated by subscript 1 and the lower fluid by 2. The mean

velocities and densities are

ii,

,ii

and PI ,Pz, respectively. The pressures are PI =

p(z) +

p;(x,z,t)

and pz = p(z) +

p~(x,z,t)

where

ap = {-PIg, z > 0 (2.152)

-P2g, z < 0

The undisturbed height of the interface is taken to be z = 0, while the height

ofthe

disturbed interface relative to the undisturbed height is represented by h. We

consider the range of

x for which h < 0 and integrate the vertical equation of

motion from z

-00

00.

In carrying out the integration, we have three versions

of the linearized vertical equation of motion to consider:

(

a a),

ap2

- +

- w2

= - -

for z < 0 below the interface

(

+ iiI

~)w;

= -

ap;

(pz

-PI )

for z < 0 above the interface (2.154)

(

~)w;

; ,

for z > 0 above the interface

36 See Lamb (1932).