Houze Robert A., Jr. Cloud Dynamics
Подождите немного. Документ загружается.


4.3 Polarization Data 119
Figure 4.2 Typical
ZDR
values for raindrops of various sizes and hail. Black arrows on the hail
particle represent tumbling motions. (Adapted from Wakimoto and Bringi, 1988. Reproduced with
permission from the American Meteorological Society.)
values are low partly because ice particles do not generally exhibit a preferred
orientation as they fall. Ice crystals and snowflakes may be flat; however, they
oscillate or tumble as they fall, so that their axes are rather randomly oriented.
Hail particles also tend to tumble or spin as they fall, as indicated in Fig. 4.2.
Thus, regions of snow or hail particles exhibit no preferred orientation and hence
have near-zero values of
ZOR.
Echoes produced by rain can therefore often be
distinguished from those produced by ice particles by whether or not they have a
finite value of
ZOR.
Another reason the
ZOR
of signals returned from ice particles is generally low is
related to the nature of the interaction that occurs when electromagnetic radiation
impinges on a particle of low complex index of refraction. An extreme aspect ratio
is required to produce a measurable
ZOR
(similar to CDR) in this case. This
condition is eased when the ice particles are wet and thus have a larger complex
index of refraction. Consequently, large and wet ice particles tend to produce a
noticeable signal, if the particles have a preferred orientation. These conditions
prevail in the melting layer, which produces a strong signal. Thus, differential
reflectivity
ZOR
can be used to distinguish between ice and water, to delineate the
melting layer, and to indicate the mean drop size in the rain.
According to (4.26), the linear depolarization ratio LDR is a measure of how
much of the transmitted signal is depolarized. In general, precipitation particles
depolarize propagating electromagnetic waves only if they are aspherical and if
they have no axis of symmetry parallel to the direction of the wave polarization.
Therefore a spherical particle illuminated by horizontally transmitted radiation
produces an echo pulse that is purely horizontally polarized. All of the vertical
components of electric field oscillation excited within the sphere by the horizon-
tally polarized wave cancel by symmetry (i.e., no net depolarization occurs).
Hence, only horizontal components are returned to the radar, and LDR
=
-00.
Ifa

120 4 Radar Meteorology
particle is elongated and not oriented either purely horizontally or purely verti-
cally, then the oscillations parallel to the long axis of the particle predominate, and
the returned signal has both a horizontal and a vertical component (i.e., part of the
transmitted wave has been depolarized). Thus, LDR
>
-00.
The more strongly the
transmitted radar waves are depolarized by precipitation particles, the stronger
the backscattered cross-polar signal will be and thus the larger (i.e., the less
negative) the LDR becomes. Since the cross-polar signal is generally smaller than
the copolar signal, LDR never exhibits positive values. Regions of snow charac-
terized by flat ice particles of varying orientation tend collectively to produce a
measurable value of LDR. However, the small index of refraction of ice might
suppress the magnitude of the expected shape effects. The LDR values are dra-
matically enhanced (less negative) for wet ice particles because of the increased
complex index of refraction. LDR has typical values of
-10
to
-20
for melting ice
to - 25 to - 30 for ice particles or rain. Thus, the linear depolarization ratio LDR is
an excellent indicator of the melting layer and also provides some information
about the shape and fall behavior of the precipitation particles.
4.4 Doppler Velocity Measurements
The information derived from reflectivity and polarimetric data, as described in
Sees. 4.2 and 4.3, is related primarily to the physics of the precipitation producing
the signals returned to the radar. The same signals can be further processed to
obtain information on the motions of the precipitation particles and of the air in
which they are located. This processing takes advantage of the Doppler-shifted
frequency of the echoes. The kinematic information derived in this manner allows
the precipitation measurements to be viewed in the context of the circulation of air
through the storms producing the precipitation. Since radars operating at
3-1
O-cm
wavelengths are sometimes sufficiently sensitive to receive echoes from clear air,
mainly from turbulent fluctuations of the index of refraction of the air and/or from
insects, aspects of the air motions in the environments of storms can also be
detected. The clear air echoes are returned primarily from the boundary layer, and
they can be useful for mapping the flow of boundary-layer air into and out of the
storm. They are also useful for analyzing the boundary-layer air motions that exist
before and after precipitating cloud systems
OCCUr.
97
Most of the techniques de-
scribed below in
Sees, 4.4.1-4.4.7 are applicable to the processing of both clear air
echoes and echoes from precipitation particles.
4.4.1 Radial Velocity
If a target detected by a radar is moving, the phase
cPP
of the reflected waves
changes with time at a rate
(4.27)
97 See Gossard (1990)for a review of radar observation of the boundary layer.

4.4 Doppler Velocity Measurements
121
where the radial velocity VR is the component of the velocity of the target parallel
to the beam of the radar. Thus,
VR can be determined from
d1>p/
dt. This principle
is the same as that of a police radar used for detecting the speed of an automobile,
except that the back scattered radiation comes from the population of targets
(usually precipitation particles) in the radar resolution volume, rather than from a
single target, and these scatterers are all moving at somewhat different veloci-
ties.?"
For
one pulse of emitted and received radiation, the radar detects the net
amplitude
(lEI) and phase
(1)p)
of the returned electric field vector E, which is the
vector sum of all the electric field vectors returned by individual scatterers. Each
successive pulse received provides a new estimate of the net
E. Vector subtrac-
tion of the net E vectors of two successive pulses yields an estimate of the net
phase difference
6.1>p
between the two pulses. Vector averaging of the net E
vectors
ofthe
two successive pulses yields the vector average E, whose amplitude
is
lEI.
A new vector given by
(lEI,
6.1>p)
may then be formed for each pulse pair.
The vector average of
(lEI,
6.1>p)
from a number of successive pulse pairs can be
calculated to improve the estimate of this vector. The phase of the vector that
results from the average, which we will call
6.1>p,
is an improved estimate of the
net phase change. The estimate
6.1>p
is substituted in (4.27) to obtain an estimate of
the
mean
radial velocity VR .99
The amplitude of the vector that results from the average of
(lEI,
6.1>p)
over
several pairs of pulses is related to the average power
P
r
returned by the scatterers
in the resolution volume, since it can be
~own
that the amplitude of the returned
electric field vector is proportional to
V P,.100 Since the mean radial velocity VR
estimated by the above-described vector averaging is weighted by
lEI
it may be
regarded as the mean of the
Doppler
velocity
spectrum,
which is the distribution
of power returned from the sampling volume expressed as a function of radial
velocity. This spectrum may be denoted
S(VR),
where
S(VR)
dV
R
is the amount
of returned power accounted for by targets with radial velocities between
VRand
V
R
+
dV
R
•
It
is related to P
r
by
(4.28)
The mean radial velocity
V
R
,
defined as the mean (first moment) of this distribu-
tion, may be written as
(4.29)
98 Actually, a police
radar
is a much simpler device than a meteorological radar since it measures
only the speed and not the location of the target. However, the speed of the target is determined by the
rate of phase angle change in either case.
99
For
further discussion of Doppler
radar
velocity estimation, see Sirmans and Bumgarner (1975).
100 See Doviak and Zrnic (1984, pp. 34-38).

122 4 Radar Meteorology
The Doppler velocity spectrum
S(V
R) contains several types of useful informa-
tion.
For
example, when the antenna is pointing horizontally, a sharply bimodal
spectrum of radial velocity
can
indicate the presence of a tornado (see Sec. 8.8)
lying in the beam of the radar. Or if the antenna is pointing vertically, the Doppler
spectrum
can
be related to the particle size spectrum of falling precipitation (see
Sec. 4.4.3). The variance (i.e., the second moment) of the Doppler spectrum
contains information related to the
shear
and
turbulence of the air motions pro-
ducing the Doppler velocities.
Although the radial velocity spectrum contains some useful information, most
work with Doppler
radar
data
considers only the power-weighted mean radial
velocity V
R
•
This means target velocity can be related to air motions and particle
fall speeds through the geometry of the pointing angle of the antenna.
If
we
assume that the scatterers detected by the radar move horizontally with the wind
and vertically as a combination of vertical air motion and (in the case of precipita-
tion particles) fall speed V
T
,
then
V
R
= (u sina
a
+ v cosa
a
)
cosa
e
+
(w
- V
T
)
sin a
e
(4.30)
where
au is the azimuth angle (measured clockwise from the north) toward which
the radar beam is pointing, and
a.
is the elevation angle. The angles are always
known, and they
can
be varied by pointing or scanning the antenna in various
directions. Ways
can
be devised to direct the beams of one or more radars such
that information about the wind components
(u,v,w)
and the fall speed V
T
can be
derived from the measurement of V
R.
The main strategies used are summarized in
Sees. 4.4.3-4.4.6.
4.4.2 Velocity
and
Range Folding
Since the
radar
emits pulses of radiation at a set frequency (called the pulse-
repetition frequency, or
PRF),
the radial velocity of a target VR can be determined
by comparing the phases of the signals reflected
back
to the antenna from two
successive pulses. The radar-detected difference in phase angle
il<pp
between
successive pulses is a
number
between -1T and
+1T.
Since the pulses are separated
by a finite interval of time
ill,
we could in principle determine V
R
from (4.27).
However, since the phase is not monitored continuously during the interval
ill,
there is no way to be certain that the true phase change is
not
the detected
difference plus some integral multiple of
±21T.
Hence, the detected radial velocity
is unambiguous only if the actual velocities of the targets are never so large that
they produce a true phase change outside the range of
±
1T,
that is, if they move
less than a quarter of a
radar
wavelength in the interval between two successive
pulses [recall (4.27)]. The unambiguous velocity range is then
PRp·A,
Il-RI
s 4
==
V
rnax
(4.31)
If the true radial velocity lies outside this range (or Nyquist interval), it is said to
be folded.
It
is often possible to correct for folded
data
by adding or subtracting

4.4 Doppler Velocity Measurements 123
the correct number of Nyquist intervals (2Vmax) to the detected radial velocity.
This correction (called
unfolding) is possible because the primary factor contribut-
ing to the magnitude of
V
R
is the horizontal wind velocity and (i) there is usually
some independent knowledge of the prevailing wind that can be used to indicate
the correct Nyquist interval for a given situation, and (ii) since gradients of the
wind are continuous, the correct Nyquist interval can usually be assumed to be
the one which removes discontinuities in the field of
VR •
The procedure of unfolding can be tedious and undesirable, and it would appear
that it could be avoided simply by setting the PRF to a sufficiently high value.
However, a high PRF creates another type of folding. The maximum range at
which a target can be detected before the next pulse is emitted is
Co
T. = ---'---
max
2.
PRF
(4.32)
where Co is the speed of light. The factor 2 appears because the pulse must travel
out to r
max
and back before the next pulse is emitted. Ideally, the PRF should be
set to a low enough value that
rmax exceeds the maximum range at which echoes
can be detected by the radar equipment. Otherwise a second pulse will be emitted
before the preceding pulse returns to the antenna from the distant target. The
radar will then automatically position the echo of a distant target as though it were
a reflection from the second pulse. The echo will thus be placed too close to the
radar by an amount equal to
r
max'
This type of aliasing is called range folding, and
the misplaced echoes are called
second-trip echoes.
It
is thus desirable to have the PRF set to as
Iowa
value as possible to avoid
range folding and to as high a value as possible to avoid velocity folding. Usually a
compromise is made, according to which the PRF is set to an intermediate value
for which moderate amounts of both types of folding occur. Consequently, an
important step in Doppler radar analysis is data editing, in which folded data are
eliminated or corrected.'?'
4.4.3 Vertical Incidence Observations
One way to greatly simplify the geometry in (4.30) is to hold the antenna in a
vertically pointing position. Then
V
R
= w - V
T
(4.33)
If the antenna is held in this position, a time series of (w - V
T
)
as a function of
height is obtained. In stratiform precipitation, where
Iwl
«
IVTI
(see Chapter 6),
these data become a time series of precipitation fall speed as a function of height.
In convective precipitation, where
w
~
V
T
,
the time-height series of V
R
observed
at vertical incidence can be converted to a time-height plot of vertical air velocity
101 Some Doppler radars have the capability to operate at more than one PRF, either continuously
or by alternating rapidly between low and high PRF. These capabilities allow some of the ambiguities
of range and velocity aliasing to be removed from the radar data.

124 4 Radar Meteorology
w, if an independent estimate of the particle fall speed can be obtained to substi-
tute into (4.33).
In the stratiform case, where
Iwl
«
IVTI,
it is also possible to use vertical
incidence Doppler data to study the size spectrum of raindrops. In this case,
V
R
=
V
T.
Since VT is a function only of the drop diameter, the radial velocity spectrum
S(VR) can be converted to a spectrum SeD)
ofthe
total returned power accounted
for by drops in the size range
D to D + dD. Since the returned power is propor-
tional to the sum of the sixth power of the diameter of all the particles scattering
the radiation,
SeD) is proportional to D6N(D), and the measured velocity spec-
trum evidently can be inverted to obtain the drop-size distribution
N(D).
This
procedure is made difficult, however, by the fact that the inversion requires divi-
sion by
D6. Small errors in the measurements at small drop sizes can therefore be
exaggerated greatly by division by a very small number. In addition, turbulent air
motions, which do not affect the mean velocity of the air, can broaden the Doppler
velocity spectrum in a way
that
is unrelated to particle size. This inversion method
is even more difficult to apply to ice-particle spectra, since the fall velocity of
snow depends not only on particle size but also on particle shape and density. In
principle, the inversion of the Doppler spectrum could be applied to convective
precipitation if the air motion could be provided. However, the turbulence effects
on the spectrum become overwhelming.
4.4.4 Range-Height Data
Another way to simplify the geometry in (4.30) is to consider data at a single
azimuth angle
Ola while the elevation angle Ole is varied by scanning through a range
of 0° to about 20°. At these quasi-horizontal angles, the second term in (4.30) is
small, and
(4.34)
where
Va is the magnitude of the horizontal wind velocity component in the
azimuthal direction. This method can be used to study quasi-two-dimensional
phenomena, such as fronts, hurricanes, or squall lines.
102If the azimuth angle Ola is
directed normal to the echo line, then the velocity component
Va
determined from
(4.34) is the cross-line component of the airflow. If the airflow has little variation
in the along-line direction, then the cross-line derivative of
Va can be computed
and integrated vertically to obtain the vertical component of the flow from the
two-dimensional form of the anelastic mass continuity equation (2.54).
4.4.5 Velocity-Azimuth Display Method
If
the region surrounding a radar is characterized by winds that vary approxi-
mately linearly (in the horizontal) across the region, one may obtain a consider-
102 As discussed in Chapter 9, a squall line is a type of mesoscale convective system that exhibits a
line of cumulonimbus, which can sometimes be approximated as two-dimensional.

4.4 Doppler Velocity Measurements 125
able amount of information about the horizontal wind, its divergence and defor-
mation, and the vertical air motion by scanning the antenna through a full revolu-
tion of azimuth,
CX
a
= 0 to 360°, while holding the elevation angle
CX
e
fixed, that is,
by obtaining measurements on the surface of an inverted cone centered on the
radar and extending up through the region of echo. Echoes with winds varying
linearly across the region might be encountered either in clear-air echo or in a
region of stratiform precipitation.
The data collected on the surface of the inverted cone can be analyzed by a
technique called the
velocity-azimuth
display (V
AD)
method. 103 This method con-
siders a circle of radius
r, described by the intersection of the cone with a level
surface at a fixed altitude above the radar. The wind components
u and v are
assumed to vary linearly in
x and y across the region of the circle and to be
constant in time over the observation period.
V
T
is assumed to be a constant over
the region of the circle. The wind components on the circle are then
U= U
o
+ (dU/dX)otesina
a
+ (du/dY)otccosa
a
(4.35)
v = V
o
+ (dv/dX)otcsina
a
+ (dv/dY)otccosa
a
(4.36)
where the subscript a indicates evaluation at the center of the circle
(r,
= 0) of
radar observations at a given height. Equation (4.30) may be rewritten for the
measurements on a circle surrounding the radar, with the aid of trigonometric
identities.
104
(4.37)
where
and
[
]
r
cosa
a
z
=
(dU/dy)o
+
(dv/dX)o
c 2 e
(4.38)
(4.39)
(4.40)
(4.41)
(4.42)
The wind field in the neighborhood of a point where the wind varies linearly in
the horizontal can be decomposed into components called translation, divergence,
rotation, stretching deformation, and shearing deformation.
105If the radar location
103 The basic method was demonstrated by Browning and Wexler (1968). Refined versions of the
technique have been developed by Srivastava
et al. (1986) and Matejka and Srivastava
(1991).
104 Specifically, sin? x =
(I
- cos 2x)/2, cos? x =
(I
+ cos 2x)/2, and sin x cos x = (sin 2x)/2.
105 See Haltiner and Martin (1957, pp. 292-293) or Saucier (1955, pp. 316-319).

126 4 Radar Meteorology
is taken as the central point, all of these components except rotation can be
deduced from the coefficients in (4.37). These coefficients have the form of
Fourier coefficients. Therefore, the radar measurements of the velocity
V
R
on a
circle surrounding the radar provide the left-hand side of (4.37) as a function of
aa,
and the coefficients can be determined by standard methods of harmonic decom-
position.
The rotational component of the wind cannot be determined from the coeffi-
cients because it depends on the wind tangential to a circle surrounding the point,
and the radar measurement of
VR is made up of velocity components along the
beam, which are always perpendicular to the circle surrounding the radar. The
radar data therefore contain no information on rotation.
The translational component of the wind field is the horizontal wind vector at
the center of the circle
(u
o
,vo).
It
is determined from the coefficients al and b, ,
since the azimuth angle is given. By analyzing the data obtained on circles over a
range of heights, the vertical profile of the wind velocity is obtained. Since the
azimuth at which the horizontal velocity component along the beam of the radar is
zero is orthogonal to the vector wind direction, the shape of the zero radial
velocity contour in a polar coordinate display of the radial velocity data on a
conical surface indicates the sense of the wind shear. As shown in Fig. 4.3, an
S-shaped contour indicates veering wind (i.e., a wind whose direction is changing
in the clockwise
sense-northerly
to easterly to southerly to westerly), while a
backward S indicates backing wind (direction changing in the counterclockwise
sense). This method is used to determine wind profiles in the clear air boundary
layer and in stratiform precipitation with radars of centimetric wavelengths. A
similar procedure is used to derive winds from
UHF
and
VHF
profilers.
The term in brackets in (4.41) is the shearing deformation of the wind field
centered at r
c
= 0, while that in (4.42) is the stretching deformation. They are
determined from the coefficients
az and
bi,
respectively. As we will see in Chapter
11, the deformation components of the wind field play an important role in fronto-
genesis, and these properties of the wind field are therefore particularly useful in
analysis of frontal precipitation systems.l'"
The term in brackets in (4.38) is the divergence of the wind field.
It
is not,
however, straightforward to determine from the value of the coefficient
as, since
this coefficient depends on two unknowns, the divergence and
(w - V
T
) .
There-
fore, it is necessary to measure
V
R
around at least two circles at the same altitude.
From the two estimates of
as, both the divergence and (w - V
T
)
can be deter-
mined.
It
is better to obtain
a.,
around several circles and determine the divergence
and
(w - VT) that best fit all
ofthe
data. Once the divergence is obtained, it can be
substituted into the anelastic continuity equation (2.54), and the vertical air veloc-
ity
w can be obtained by integrating vertically, if a boundary condition (e.g., zero
vertical velocity at echo top) can be reasonably assumed.
VAD analysis is one of the best ways to obtain the vertical air motion in
stratiform precipitation.
It
is also one of the best ways to estimate particle fall
106 For an example of this use of radar data, see Carbone et al. (1990).
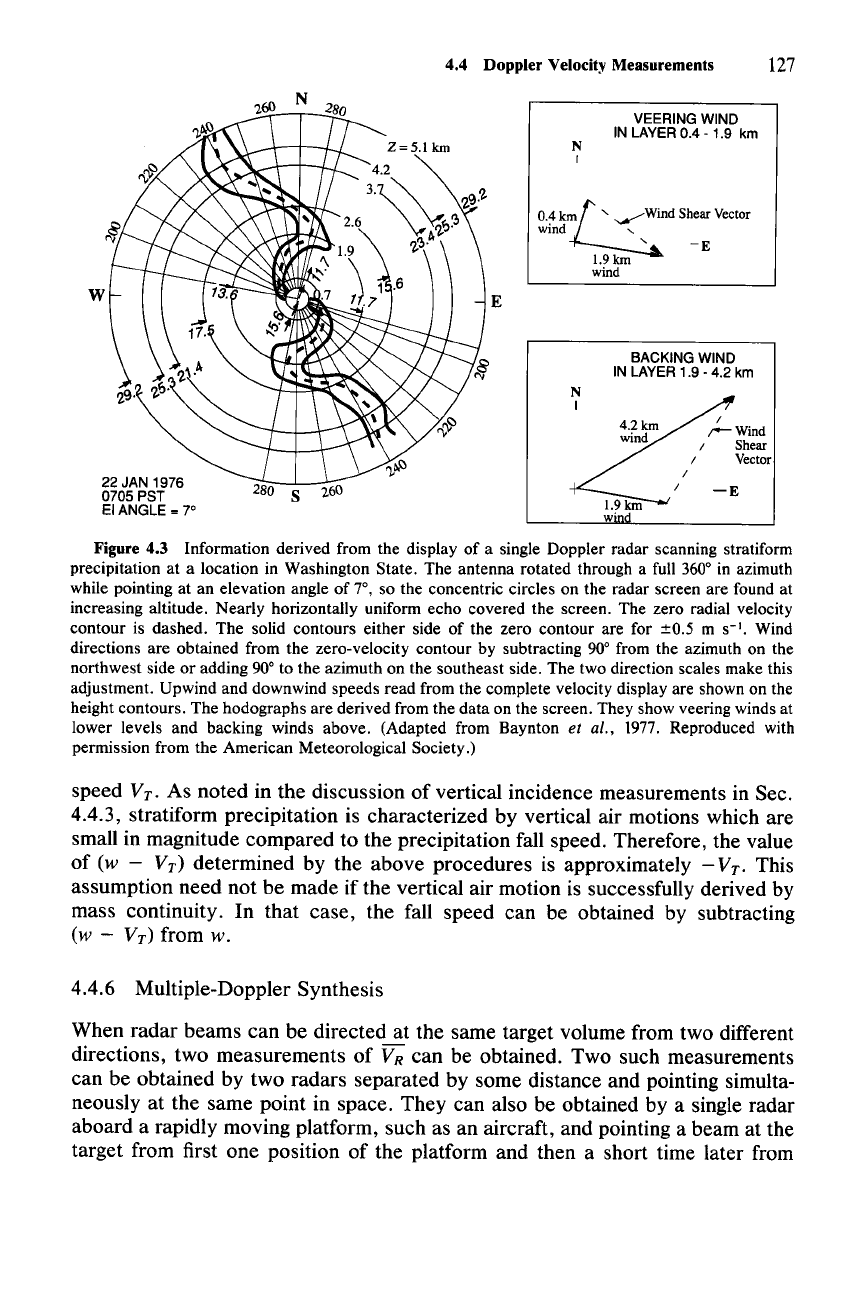
4.4 Doppler Velocity Measurements
127
w
22 JAN 1976
0705 PST
EIANGLE
= 7°
E
VEERING WIND
IN LAYER 0.4 • 1.9 km
N
I
0.4<i:Shear Vector
wind -,
-,
-E
1.9km
wind
BACKING WIND
IN LAYER 1.9 - 4.2 km
Figure 4.3 Information derived from the display of a single Doppler radar scanning stratiform
precipitation at a location in Washington State. The antenna rotated through a full 360° in azimuth
while pointing at an elevation angle of 7°, so the concentric circles on the radar screen are found at
increasing altitude. Nearly horizontally uniform echo covered the screen. The zero radial velocity
contour is dashed. The solid contours either side of the zero contour are for ±0.5 m
S·I.
Wind
directions are obtained from the zero-velocity contour by subtracting 90° from the azimuth on the
northwest side or adding 90° to the azimuth on the southeast side. The two direction scales make this
adjustment. Upwind and downwind speeds read from the complete velocity display are shown on the
height contours. The hodographs are derived from the data on the screen. They show veering winds at
lower levels and backing winds above. (Adapted from Baynton
et al., 1977. Reproduced with
permission from the American Meteorological Society.)
speed V
T
•
As noted in the discussion of vertical incidence measurements in Sec.
4.4.3, stratiform precipitation is characterized by vertical air motions which are
small in magnitude compared to the precipitation fall speed. Therefore, the value
of
(w - VT) determined by the above procedures is approximately - VT. This
assumption need not be made if the vertical air motion is successfully derived by
mass continuity. In that case, the fall speed can be obtained by subtracting
(w - V
T
)
from w.
4.4.6 Multiple-Doppler Synthesis
When radar beams can be directed at the same target volume from two different
directions, two measurements of
V
R
can be obtained. Two such measurements
can be obtained by two radars separated by some distance and pointing simulta-
neously at the same point in space. They can also be obtained by a single radar
aboard a rapidly moving platform, such as an aircraft, and pointing a beam at the
target from first one position of the platform and then a short time later from

128 4 Radar Meteorology
another position. These methods of obtaining dual-Doppler radar data are proba-
bly the most common; however, many other strategies can be imagined. Whatever
the strategy used to obtain them, the data derived from the same target by two
beams originating from different locations provide two relations of the form (4.30).
Each beam corresponds to a different azimuth-elevation pair
(au
,a
e
)
and provides
a different value of
V
R.
However, four variables are sought for each point ob-
served by the two beams
(u,v,w,
and V
T
) .
Some assumption must be made to
obtain
V
T
• Since the reflectivity is measured at each point at which V
R
is mea-
sured, the typical procedure is to invoke a reflectivity fall speed relation of the
form (4.13). It remains to determine the vertical air motion
w.
For
this purpose,
the anelastic continuity equation (2.54) is employed. Since this equation relates
the wind components
u, v, and W to each other, it provides the final physical
relationship required to close the problem. However, since the continuity equa-
tion is a differential equation relating the horizontal derivatives of
u and v to the
vertical derivative of
w, some further problems arise. First, the continuity equa-
tion must be integrated vertically, and appropriate boundary conditions must be
supplied at the top and/or bottom of the volume containing the radar echo. Since
echoes do not always extend to cloud top or to the ground, where
W may readily
be assumed zero, the choice of a boundary condition is sometimes difficult. Sec-
ond, a basic-state density profile
piz)
must be provided. Usually, it can be based
on nearby sounding data or simply on climatology. The effect of this exponentially
varying density weighting in the anelastic continuity equation is that the equation
must typically be integrated downward to avoid the rapid accumulation of errors
resulting from the large air density at low levels. Third, since the horizontal
derivatives of the velocity are required to apply the continuity equation, three-
dimensional fields of
u and v are required. A commonly followed procedure is to
make a first guess of
w at each data point to solve (4.30) for an initial estimate of u
and v. Then, these values are used in the continuity equation to make a second
estimate of
w to substitute in (4.30), and so on. Iterations are performed until the
fields of
u, v, and w converge. When they do, the three-dimensional wind field
within the region of radar echo is said to be
synthesized.
The iteration
just
described is not always necessary. Two Doppler radars can
be located some distance apart and coordinated in their scanning such that they
simultaneously scan the same tilted planes intersecting the baseline running be-
tween them. The continuity equation can be transformed to a cylindrical coordi-
nate system centered on the baseline. If again some assumption is made to obtain
the fall speed, this form of the continuity equation can be solved for the velocity
orthogonal to the planes scanned given the observed radial velocities in scanned
planes. The velocities obtained can then be transformed geometrically to
u, v, and
w. This technique is called coplane scanning. 107
Uncertainties in the determination of the wind field by multiple-Doppler radar
can be reduced if a third radar beam is directed at all the targets in a given region.
The additional information from the third radar can be used in two ways. In
107 Coplane scanning was devised by
Lhermitte
(1970).
