Холоднов В.А. Системный анализ и принятие решений. Компьютерное моделирование и оптимизация объектов химической технологии в MathCad и Excel
Подождите немного. Документ загружается.


201
025zyx
222
В примерах 3 и 4 для решения задач оптимизации используется встроенная
функция minimize.
Пример 3
x
y
z
u1
u2
u3
v1
v2
Find x y z u1 u2 u3 v1 v2( )
x
y
z
u1
u2
u3
v1
v2
3.603
0.211
3.46
0
0
0
0.7
0.297
Проверка
1000 x
2
2 y
2
z
2
x y 974.195
8 x 14 y 7 z 56 0
Решение задачи условной оптимизации
Минимизировать
f x y( ) x
2
y
x
при ограничениях
x
y
= 6
x 1
0
x
2
y
2
26
Задание минимизируемой функции
f x y( ) x
2
y
Задание начальных приближений
x
8
y
6
Given
x y 6 0
x
1
x
2
y
2
26
p
1
5
Решение задачи
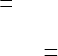
202
Пример 4
В примере 5 показано решение традиционных задач минимизации функции
p Minimize f x y( )
x p
1
y p
2
26 x
2
y
2
1.875 10
5
Проверка
x 1( ) 2.344 10
6
x y( ) 6 0
Решение задачи условной оптимизации
Минимизировать
f x y z( ) 1000 x
2
2 y
2
z
2
x
y
при ограничениях
x
2
y
2
z
2
25
= 0
8x + 14y + 7z - 56 = 0, x >= 0 y >= 0 z >= 0
Задание минимизируемой функции
f x y z( ) 1000 x
2
2 y
2
z
2
x
y
Задание начальных приближений
x
3.5
y
0.2
z 3.5
Решение задачи
Given
x
2
y
2
z
2
25
0
8 x 14 y 7 z 56
0
x
0
y
0
z
0
p Minimize f x y z( )
p
4.846
1.231
0
x p
1
y p
2
z p
3
Проверка
8 x 14 y 7 z( ) 56 1.421 10
14
1000 x
2
2 y
2
z
2
x y 967.521
x
2
y
2
z
2
25 2.073 10
7

203
Розенброка и функции Пауэлла в Mathcad, которые используются при
тестировании методов оптимизации.
Пример 5
На примерах 6 и 7 показано решение достаточно сложных задач оптимизации.
Пример 6
Минимизировать функцию Розенброка
f x y( ) 100 x y
2
2
1 x( )
2
Задание начальных приближений
x
0.2
y
0.06
Решение задачи
p Minimize f x y( )
p
1
1
x p
1
y p
2
f x y( ) 8.517 10
12
Минимизировать функцию Пауэлля
f x y v z( ) x 10 y( )
2
5 v z( )
2
y 2 v( )
4
10 x z( )
4
Задание начальных приближений
x
0.5
y
0.5
v
0.1
z
0.1
Решение задачи
var Minimize f x y v z( )
var
0.019
1.87 10
3
0.029
0.029
x var
1
y var
2
v var
3
z var
4
f x y v z( ) 1.294 10
5
Минимизировать тестовую функцию
f x y v z( )
1
10
a
v exp
a
10
x
z exp
a
10
y
exp
a
10
5 exp a( )
2
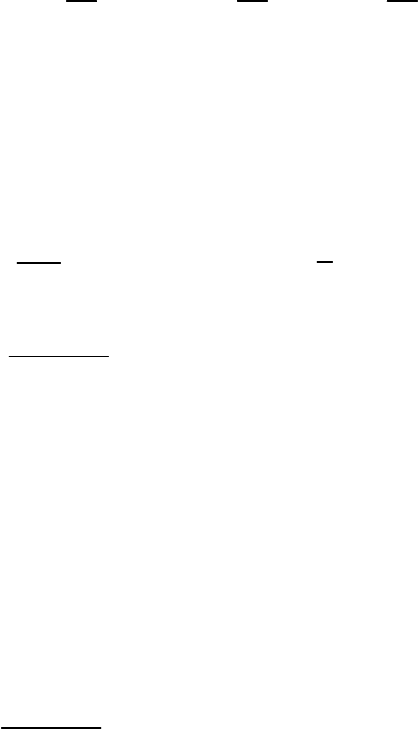
204
Пример 7
8.6 Решение задач оптимизации химико-технологических процессов
8.6.1 Определение оптимальных параметров эрлифтного аппарата
Требуется найти конструктивные оптимальные параметры эрлифтного аппарата
(устройство для разделения жидкостей, подъема нефти или воды из буровых
скважин), при которых капитальные затраты минимальны.
Капитальные затраты эрлифтного аппарата могут быть определены по
уравнению:
Задание начальных приближений
x
1
y
2
v
1
z
1
p
1
10
1
5
Решение задачи
p Minimize f x y v z( )
f x y v z( )
1
10
a
v exp
a
10
x
z exp
a
10
y
exp
a
10
5 exp a( )
2
x p
1
y p
2
v p
3
z p
4
f x y v z( ) 2.455 10
11
w
i
i
100
Минимизировать тестовую функцию
i 1
99
y
i
25 exp
2
3
ln 50 ln w
i
f x v z( )
1
99
i
exp
y
i
z
v
x
w
i
2
f x v z( )
1
99
i
exp
y
i
z
v
x
w
i
2
f x v z( ) 0.025
Задание начальных приближений
x 250
v
0.3
z
5
Решение задачи
p Minimize f x v z( )
p
311.461
2.032
21.847
x p
1
v p
2
z p
3
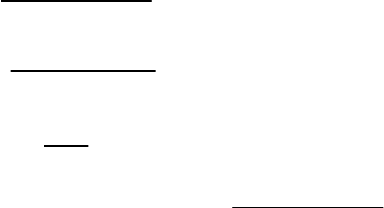
205
,1072d339
V226d1588V95Vd7736727d2622V13378248340K
22
2
где
V
– объем аппарата, м
3
;
d – диаметр аппарата, м;
– угол раскрытия конического днища, рад.
В соответствии со справочными данными для эрлифтных аппаратов
конструктивные параметры могут находиться в диапазонах: ]16,4[V
,
]6.0,3.0[d
, ]50,20[
град.
Итак, имеем задачу оптимизации с ограничениями на управляющие переменные в
виде неравенств.
Задача сформулирована так, что не требует предварительной подготовки для
задания функции цели.
Выбор начальных приближений (стартовой точки) не представляет трудностей.
Приближениями будут значения конструктивных параметров аппарата, а
диапазоны для них заданы по условию. В виду того, что анализ факторного
пространства не производился, решение необходимо повторить несколько раз из
разных исходных точек, чтобы выбрать глобальный оптимум, если существует
несколько решений.
Для первой стартовой точки выбираем значения на левой границе заданных
диапазонов. Две других точки задаем для правой границы и для середины
диапазонов.
При решении задачи следует использовать блоки Given….Minerr или Given….
Minimize, в которых должны быть учтены ограничения на конструктивные
параметры (управляющие переменные). Пример решения представлен ниже.
Задание целевой функции
k1 V d
248340 13378 V 2622 d 6727
773 V
d
k2 V d
95 V
1588 d
1226 V
2
339 d
2
1072
2
k V d
k1 V d
k2 V d
Задание ограничений на управляющие воздействия
Vmin
4
Vmax 16
Vcp
Vmin Vmax
2
dmin
0.3
dmax
0.6
dcp
dmin dmax
2
min 20
max 50
per x( )
x
180
min per
min
max per
max
cp
min
max
2
Решение задачи оптимизации для левой границы диапазона
min
d
dmin
V
Vmin
206
В начале целевая функция записана в виде функции пользователя. Для удобства
восприятия она разбита на две составляющие. При задании значений диапазона
для параметра
предусмотрен перевод данных из градусов в радианы.
Решение проводилось из трех стартовых точек. После задания координат в
каждой точке вычислялось значение целевой функции. Затем решалась задача
оптимизации. При решении использован блок Given….. Minimize.
Все варианты приводят к одному результату. Значения параметров в
оптимальной точке
873.0
6.0
4
x , а значение целевой функции
K
= 3.14110
5
.
Это дает основание считать, что целевая функция имеет один оптимум.
Given
V
Vmin
V
Vmax
d
dmin
d
dmax
x1 Minimize k V d
Решение задачи оптимизации для правой границы диапазона
V Vmax
d dmax
max
Given
V
Vmin
V
Vmax
d
dmin
d
dmax
x2 Minimize k V d
Решение задачи оптимизации для середины диапазона
V
Vcp
d
dcp
cp
Given
V
Vmin
V
Vmax
d
dmin
x3 Minimize k V d
Результаты решения задачи оптимизации
x1
4
0.6
0.873
x2
4
0.6
0.873
Значение целевой функции в оптимальной точке
k x1
1
x1
2
x1
3
3.141 10
5
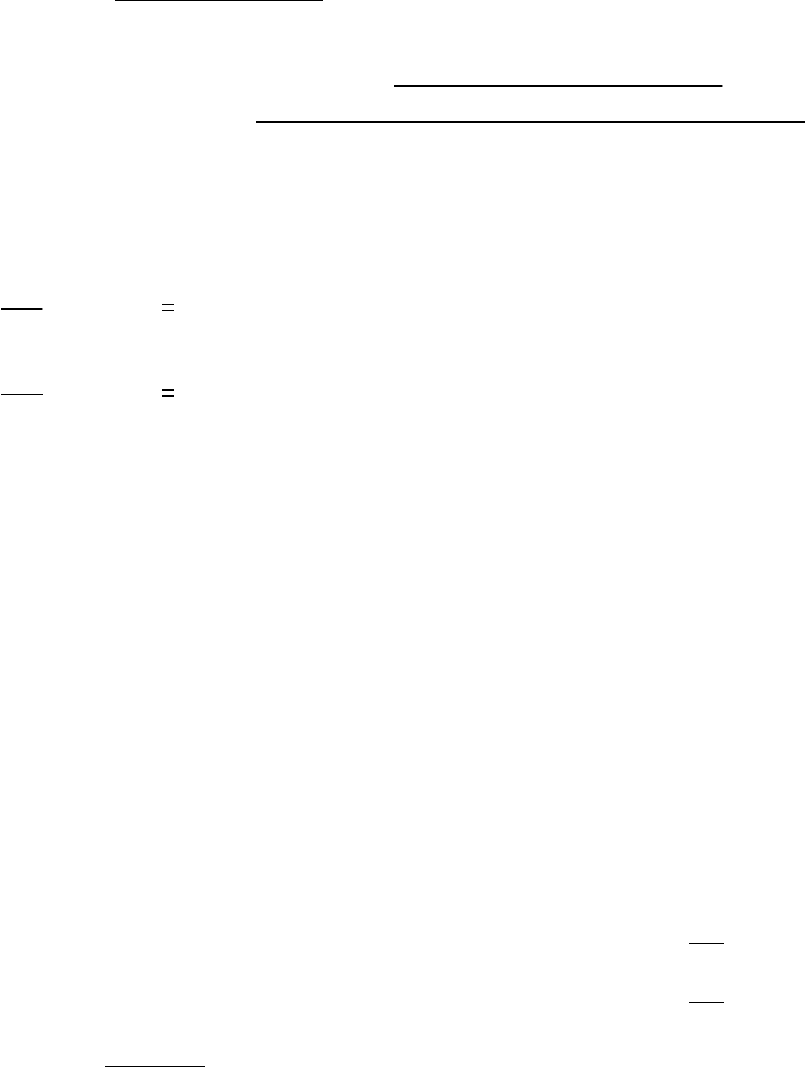
207
8.6.2 Оптимизация теплообменной подсистемы
Ниже показано решение задачи оптимизации теплообменной системы,
представленной на рисунке 8.1.
8.6.3 Оптимизация химико-технологического процесса в каскаде реакторов
В каскаде из трёх реакторов с мешалкой протекает обратимая реакция BA
.
Константа скорости прямой реакции
)
RT
E
433.12exp(k
i
1
i,1
Константа скорости обратной реакции
)
RT
E
809.16exp(k
i
2
i,2
R = 1.985
Ккмоль
ккал
k1 120
k2 80
k3 40
w 100000
F1 500
F2 1000
g1 F1( )
300 w 100 k1 F1
k1 F1 w
F F1 F2( ) F1 F2
w g1 F1( )
400 w k2 F2 400 g1 F1( )( )
k2 F2 w
300
k3 100
Given
F1
0
F2
0
F1
F F1 F2( )
d
d
0
F2
F F1 F2( )
d
d
0
F1
F2
Minerr F1 F2( )
F1
F2
579.307
1.36 10
3
Given
F1
0
F2
0
F1 p
0
F2 p
1
F F1 F2( ) 7.049 10
3
p
579.307
1.36 10
3
p Minimize F F1 F2( )

208
Энергии активаций реакций составляют:
9200E
1
кмоль
ккал
и
12500
E
2
кмоль
ккал
.
Здесь i – номер реактора, i = 1, 2, 3.
Обозначим концентрации веществ на входе в систему
bxbx
b,a
3
м
кмоль
.
При этом известно, что
1a
bx
,
0b
bx
.
Концентрации на выходе i-го реактора
ii
b,a
3
м
кмоль
.
На выходе из системы реакторов концентрации веществ составляют:
8.0b,2.0a
3
3
Среднее расчетное время пребывания:
i
(с).
Определить такие значения
i
и температуры
i
T в реакторах, чтобы суммарное
среднее расчетное время пребывания было минимальным.
Рассчитать при найденных оптимальных значениях
i
и
i
T концентрации веществ
на выходе каждого реактора.
Уравнения материального баланса по веществу А:
)bKaK(aa0
ii,2ii,1ii1i
,
bx0
aa .
Уравнения материального баланса по веществу В:
)bKaK(bb0
ii,2ii,1ii1i
,
bx0
bb .
На примере, представленном ниже показано решение задачи оптимизации для
случая заданной температуры в реакторах каскада.
kr1
12.433
kr2
16.809
R
1.985
a0
1
E1 9200
E2 12500
T1 328
T2
291
T3
274
1 20
2
57
k1 T( ) exp kr1
E1
R T
k2 T( ) exp kr2
E2
R T
3
1
2
a2
1
2
0.2
k1 T3( ) 0.2 k2 T3( ) 0.8( )
a1
1
a0
1 k2 T1( )
1
1 k1 T1( ) k2 T1( )( )
a2
1
2
a1
1
2 k2 T2( )
1
2 k1 T2( ) k2 T2( )( )

209
На следующем примере показано нахождение оптимальных значений времен
пребывания и температуры в каждом реакторе каскада. Критерий оптимизации,
как и в предыдущем примере, представляет собой суммарное время пребывания.
F
1
2 T1 T2 T3
1
2
3
1
2 T1 T2 T3
F
1
2
1
2
3
1
2
Given
1
0
2
0
1
2
Minimize F
1
2
1
2
30.178
66.901
3
1
2
106.443
F
1
2
203.522
kr1
12.433
kr2
16.809
R
1.985
a0
1
E1 9200
E2 12500
T1 300
T2 280
T3 275
1 50
2
77
k1 T( ) exp kr1
E1
R T
k2 T( ) exp kr2
E2
R T
a1
1 T1
a0
1 k2 T1( )
1
1 k1 T1( ) k2 T1( )( )
a2
1
2 T1 T2
a1
1 T1
2 k2 T2( )
1
2 k1 T2( ) k2 T2( )( )
3
1
2 T1 T2 T3
a2
1
2 T1 T2
0.2
k1 T3( ) 0.2 k2 T3( ) 0.8( )
Given
1
0
2
0
T1
273
T1 330
T2
273
T2 330
T3 330
T3
273
1
2
T1
T2
T3
Minimize F
1
2 T1 T2 T3
1
2
T1
T2
T3
31.473
67.611
327.473
290.777
273
F
1
2 T1 T2 T3
203.793
210
8.7 Применение электронных таблиц Excel для решения задач оптимизации
Более универсальный инструмент для решения задач оптимизации представлен в
рамках Excel.
Подготовка задачи для решения в рамках Excel проводится в следующей
последовательности:
9. Выбор ячеек для поисковых переменных.
10. Задание в них координат исходной точки поиска.
11. Выбор ячейки для значения целевой функции.
12. Запись в ней формулы для её вычисления.
13. Выбор ячеек для ограничений в виде функциональных неравенств.
14. Запись в ячейках формул для их вычисления.
15. Выбор ячеек для ограничений в виде функциональных равенств.
16. Записи в ячейках формул для их вычисления.
Далее выбрав в меню “Сервис””Поиск решения” подключается один из двух
градиентных методов: метод Ньютона или метод сопряжённых градиентов.
Задаются ячейки, значения которых будут варьироваться в процессе поиска,
добавляются ограничения на переменные, задаются параметры поиска (число
итераций, способ вычисления частных производных и т.д.). По команде
“Выполнить“ осуществляется решение задачи.
Примером решения задач оптимизации может послужить функция Пауэлля, для
которой требуется найти минимум:
4422
)zx(10)v2y()zv(5)y10x()v,z,y,x(f
На рисунке 8.3 показан предварительный этап решения задачи оптимизации.
На первом этапе выбираются произвольные ячейки (например, B1-B4) для
поисковых переменных x, y, v, z. В эти ячейки вводятся координаты исходной
точки поиска (5, 0.5, 0.1, 0.1).
Далее выбирается произвольная ячейка для значений целевой функции
(например, С1) и в неё записывается формула для её вычисления.
Далее выбрав пункт меню “Сервис””Поиск решения” подключается один из двух
градиентных метода: метод Ньютона или метод сопряжённых градиентов
(Рисунок 8.4, Рисунок 8.5).
После нажатия клавиши” Добавить” задаются ограничения на переменные.
