Холоднов В.А. Системный анализ и принятие решений. Компьютерное моделирование и оптимизация объектов химической технологии в MathCad и Excel
Подождите немного. Документ загружается.

221
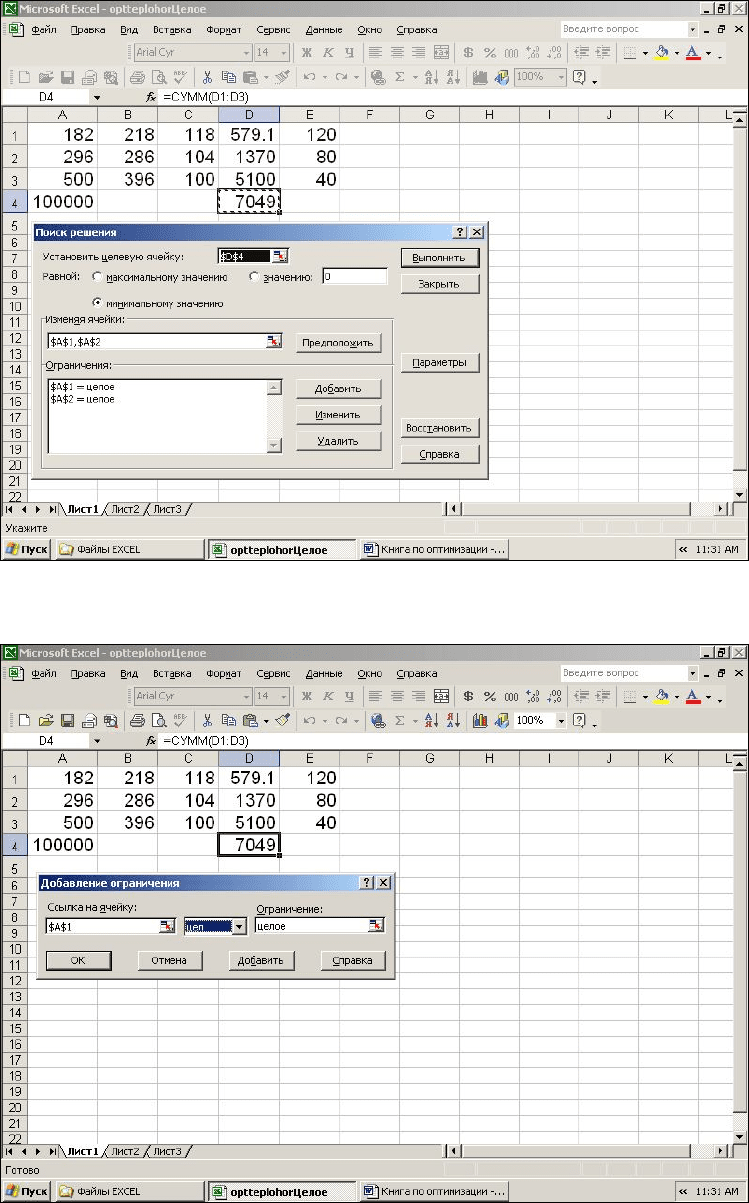
Рисунок 8.17 – Задание ограничений целого типа (начало)
Рисунок 8.18 – Задание ограничений целого типа (окончание)
Рассмотрим задачу нахождения конструктивных оптимальных параметров
эрлифтного аппарата, при которых капитальные затраты минимальны. В отличие
от ранее рассмотренной нами задачи будем считать, что конструктивные
параметры
V
и
могут принимать только дискретные значения:
)20,16,12,8,4(V
, )50,40,30,20(
град.
222
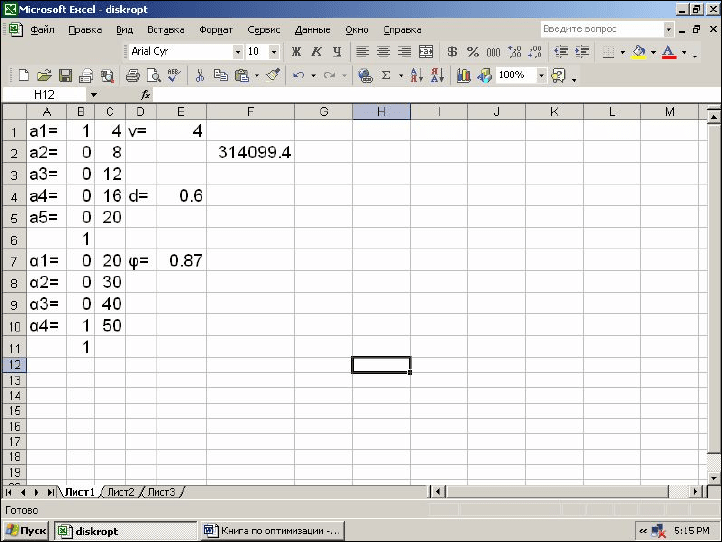
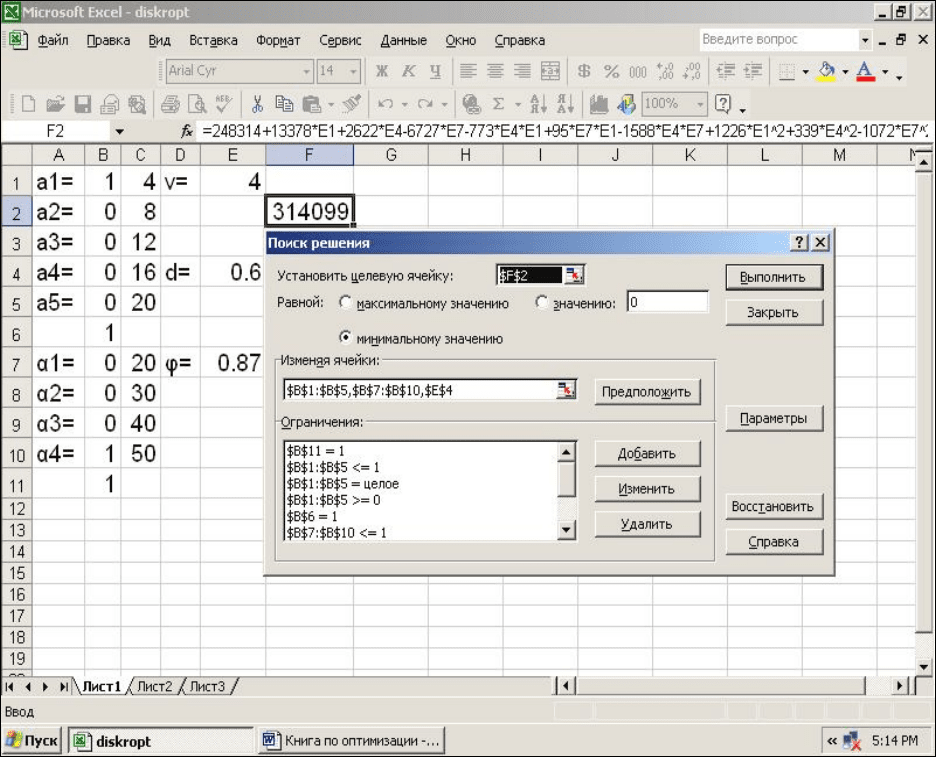
На рисунках 8.19, 8.20 показаны результаты решения задачи.
Переменная
V
определяется выражением
i
5
1i
i
VaV
,
а переменная –
4
1i
ii
b
.
В ограничениях добавлено, что
5
1i
iii
1a,1a,0a
и
i
a
целое число, а также,
что
4
1i
iii
1b,1b,0b
и
i
b
– целое число.
Рисунок 8.19 – Результаты решения задачи для эрлифтного аппарата
223
Рисунок 8.20 – Результаты решения задачи для эрлифтного аппарата

224
9 Оптимизация химико-технологических систем (ХТС) в условиях
неопределенности информации
9.1 Виды неопределенности информации
При оптимальном проектировании химико-технологических систем (ХТС)
необходимо выполнять ряд ограничений: по качеству продукта и
производительности процесса, по безопасности, экологические ограничения и
др. Проблема выполнения проектных ограничений осложняется наличием
неопределенностей в физической, химической и технологической информации, на
которой основываются математические модели ХТС. Отсюда следует, что
основная задача проектирования, которая заключается в определении
оптимальной структуры, размеров аппаратов и режимов функционирования ХТС
должна решаться с использованием неточных математических моделей в
условиях рыночной экономики. В силу этого обстоятельства в литературе в
последнее время большое внимание уделяется проблеме учета
неопределенностей при решении задач оптимального проектирования ХТС.
Степень неопределенности исходной информации зависит главным образом от
двух факторов:
– неточности исходных данных об условиях функционирования или
проектирования ХТС (назовем это неопределенностью исходных данных или
информационной неопределенностью);
– неточности применяемых при моделировании и оптимизации математических
моделей (назовем это модельной неопределенностью).
Кроме того, неопределенность оптимальных решений задач проектирования ХТС
вызывается следующими причинами:
– необходимостью внесения упрощений при построении математических моделей
ХТС;
– погрешностью реализации математических моделей и методов оптимизации на
ЭВМ.
Используемую при решении комплексной задачи проектирования ХТС
информацию можно разделить на три вида:
1. Детерминированная информация,
2. Вероятностная информация, характеризующую случайные величины с
известными законами и параметрами распределения (этот вид
информации иногда называется неполной),
3. Неопределенная информация, которая является статистической по своей
природе, но для нее неизвестны параметры или законы распределения.
В реальных задачах моделирования и оптимизации ХТС, как правило,
одновременно встречаются все три вида информации: одна часть информации
может задаваться в вероятностной форме, другая – детерминировано, третья –
оказывается неопределенной.
При этом в практике проектирования ХТС с полностью неопределенными
величинами приходится оперировать относительно редко, так как почти всегда
имеется возможность тем или иным способом, включая экспертные оценки
специалистов, получить какой-либо объем ориентировочной информации.
Первые два вида информации чаще всего характеризуют внутреннюю
информацию о системе. Третий вид характерен для информации о внешних
связях, определяемых взаимодействием ХТС с другими системами. В последних

225
двух случаях неопределенные параметры задаются диапазоном или возможными
вариантами их значений (интервальные оценки).
В любом случае неопределенная информация вносит в результаты решения
задач проектирования и управления значительную долю неопределенности.
Нами рассматриваются два вида неопределенности: неопределенность исходных
данных и модельная неопределенность.
Как в том, так и в другом случае для характеристики неопределенных параметров
используются либо интервальные оценки параметров, либо их представление в
виде случайных величин с известными законами и параметрами распределения.
9.2 Учет неопределенности информации
В настоящее время задачу проектирования ХТС, как правило, рассматривают как
детерминированную, заменяя неопределенные величины их наиболее
вероятными значениями. Повышения надежности проектных расчетов
добиваются умножением расчетных величин на эвристические коэффициенты
запаса. Однако такой подход может привести к завышенным коэффициентам
запаса и, следовательно, увеличивает капиталовложения в ХТС.
Неоднозначность неопределенных параметров приводит к тому, что расчетным
путем можно определить лишь зону, внутри которой каждое из решений будет
оптимальным для выбранного критерия эффективности функционирования ХТС.
Такая зона называется «зоной неопределенности оптимальных решений».
Исходя из этого, проблему неопределенности оптимальных решений можно
сформулировать следующим образом: неоднозначно определенная исходная
информация не позволяет получать однозначно определенные решения о
функционировании или развитии процессов.
Таким образом, решение проблемы оптимизации в условиях неопределенности
требует разработки методов, позволяющих ограничить «зону неопределенности»
некоторым конечным множеством решений, а также определить внутри этого
множества оптимальные или равнозначные решения.
9.3 Проектирование химико-технологических систем при наличии
неопределенности информации
Неопределенность исходной информации приводит к тому, что для разных
сочетаний исходных данных будут получены различные варианты решения
задачи оптимизации проектных расчетов. Поэтому для выбора окончательного
решения в этих условиях необходима разработка и применение специальных
стратегий и базирующихся на их основе методов. Выбор стратегии
обуславливается имеющейся априорной информацией о проектируемой ХТС, а
также рядом требований, предъявляемых к производству.
С точки зрения статистической теории решений основная задача оптимизации
при неопределенности параметров состоит в том, чтобы риск от решения,
обусловленный этой неопределенностью, был минимален. При этом под риском
понимается математическое ожидание функции потерь, которая представляет
собой проигрыш, вызванный неоптимальным решением:
)P,U,X(Fmin)P,U,X(F)P,U(PR
U
.
Математическое ожидание функции потерь в области изменения параметров
обозначают как средний риск:
dp)p()P,U,X(PR...Р
Pp
иск

226
При сложно рассчитываемой целевой функции, большой размерности векторов
управляющих переменных U и неопределенных параметров P решение такой
задачи требует серьезных затрат времени на расчет. Поэтому чаще всего
прибегают к упрощенным стратегиям, среди которых наиболее широко известны
стратегии Байеса, Вальда, Сэвиджа, Лапласа, Гурвица и их комбинации.
9.4 Стохастическое программирование – основные понятия
При моделировании и оптимизации ХТС предполагается, что известны точные
значения параметров математического описания и параметров входных потоков, т.е.
полагают, что эти величины являются детерминированными. Однако на практике
так бывает далеко не всегда. Достаточно часто точные значения просто не
существуют, так как эти величины являются случайными. Задачи оптимизации, в
которые входят случайные величины, называются задачами стохастического
программирования. Универсальных методов решения задач стохастического
программирования, пригодных для всех классов задач оптимизации, нет.
Как известно, случайной величиной называется такая величина, которая может
принять то или иное значение, причем заранее неизвестно, какое именно.
Математическое ожидание случайной величины, которое будем обозначать,
определяет ее среднее значение.
Среднее квадратическое отклонение, обозначаемое
x
, определяет разброс
значений случайной величины относительно ее математического ожидания.
Рассматривая величину
x
, следует иметь в виду, что она может описываться
двумя несколько отличающимися характеристиками.
Среднее квадратическое отклонение может быть определено как для всей
генеральной совокупности, так и для выборки. Здесь мы будем определять
среднее квадратическое отклонение только для выборки.
Третьей важной количественной характеристикой случайной величины, которая
показывает относительную величину разброса случайных величин, является
коэффициент вариабельности:
xM
x
x
.
Наиболее полной характеристикой случайной величины является закон ее
распределения. На практике наибольшее распространение получил нормальный
закон распределения. Нормальный закон имеет две формы представления:
– плотность распределения )x(f ;
– функция распределения )x(F .
Для их вычисления используются следующие зависимости:
1. Плотность распределения
2
2
2
)mx(
exp(
2
1
)x(f
,
где
xMm – математическое ожидание случайной величины;
x
– среднеквадратическое отклонение;
2. Функция распределения
x
dx)x(f)x(F
,

227
которая имеет большое практическое значение, так как эта зависимость дает
возможность определить вероятность появления случайной величины х < а.
График плотности распределения показывает, какие значения случайной
величины наиболее вероятны. Теоретически случайная величина х может
изменяться в пределах:
x
.
Однако с точностью до долей процента случайная величина может находиться в
интервале:
x3xMxx3xM
, что и принимается за пределы
изменения случайной величины.

228
10 Оптимизация ХТС в условиях интервальной неопределенности
информации
10.1 Постановка задачи
При проведении работ по математическому моделированию и оптимизации ХТС
фактически всегда исследователи сталкиваются с неполнотой и неточностью
исходной физико-химической, технологической, экономической информации. Учет
этих факторов может существенно повысить предсказательную силу выводов
математического моделирования и оптимизации.
Рассматриваются следующие источники неопределенности информации:
– исходная неточность коэффициентов в математических моделях (константы
скоростей реакций, коэффициенты межфазного обмена, коэффициенты массо- и
теплопереноса и т.д.) – модельная неопределенность;
– изменение внешних условий функционирования ХТС (характеристики внешних
потоков, температура, состав, расход и т.д.) – неопределенность исходных
данных;
– изменение экономических условий функционирования ХТС – неопределенность
исходных данных.
В этой главе для характеристики неопределенных параметров используются их
интервальные оценки.
При проектировании ХТС и интенсификации действующих производств должны
быть удовлетворены следующие требования:
– ХТС должна работать без аварийных ситуаций (например, температура в
трубках каталитического реактора должна быть ниже заданной величины,
концентрации веществ должны удовлетворять требованиям взрывобезопасности
и др.);
– должны быть выполнены технологические требования (качество продукции и
производительность процесса);
– при функционировании ХТС должны учитываться экологические ограничения
(например, выход вредных побочных продуктов не должен превышать некоторых
предельно допустимых норм).
Эти ограничения характеризуют работоспособность системы.
Выполнение этих требований существенно осложняется тем фактом, что, как
правило, приходится использовать неточные математические модели, в которых
неопределенные параметры могут принимать любые значения из некоторой
допустимой области неопределенности. Отсюда возникает важная задача
определения оптимальных коэффициентов запаса, которые могут компенсировать
неточности модели.
С учетом этих обстоятельств общую задачу условной оптимизации ХТС в
условиях неопределенности информации можно представить в следующем виде:
1. Задача стохастического программирования 1 для минимизации целевой
функции R при интервальной неопределенности параметров имеет вид:
)}x,...x,x,u,...u,u(R{minZ
m21k21
XxUu
,
Jj
__
j
0)x,u(
.
2. Задача стохастического программирования 2 для минимизации целевой функции
R с использованием характеристики неопределенных параметров в виде

229
независимых случайных величин с известными законами и параметрами
распределения имеет вид:
}))x,...x,x,u,...u,u(R{M(minZ
m21k21
XxUu
,
Jj
__
j
0)x,u(
.
Здесь:
_
u – k-вектор управляющих переменных с областью допустимых значений U,
,k,...,1q),}usupuuinf:uU;Uu(
qqqqq
_
x
– m-вектор неопределенных параметров с заданными интервалами допустимых
значений,
для задачи 1:
iiiii
xsupxxinf:xX;Xx
, )m,...,1(i
;
для задачи 2:
iiiii
x3xMxx3xM
, где
ii
x ,xM
– заданные значения
математического ожидания и среднеквадратичного отклонения случайных
величин;
)x,u(
__
j
– ограничения, которые выполняются для всех
X
x
, )J,...,1(j
m1
X
Xx
mm2211m21k21
Uu ,Xx
m21k21
dx...dx)x(p...)x(p)x(p)x,...,x,x,u,...,u,u(R...)}x,...x,x,u,...u,u(R{M
-
математическое ожидание значения целевой функции;
p
1
(x
1
),p
2
(x
2
),…p
m
(x
m
) – известные распределения плотности вероятностей
неопределенных параметров в виде независимых случайных величин.
Постановка задачи оптимизации в условиях частичной неопределенности исходной
физико-химической, технической и экономической информации отличается от
традиционной постановки задачи оптимизации без учета неопределенности
информации тем, что здесь присутствует вектор неопределенных параметров.
Неопределенность информации вызывается необходимостью внесения упрощений
при построении математических моделей ХТС, а также погрешностью реализации
математических моделей и методов оптимизации на ЭВМ. Степень детализации
математической модели того или иного аппарата химической технологии зависит от
влияния его эффективности на эффективность функционирования всей системы.
При большей степени влияния необходимо использовать детерминированные
модели, в другом случае можно ограничиться формальными моделями.
Использование формальных моделей для исследования и, особенно, для
управления крайне нежелательно в связи с практической невозможностью
прогноза, что объясняется свойством эмерджентности ХТС. Это усугубляется
неточностью определения коэффициентов модели по экспериментальным данным
и ограничениями на диапазон переменных при эксперименте. В книге отдается
предпочтение детерминированным моделям аппаратов химической технологии, в
которых основная неточность связана с определением параметров математических
моделей по экспериментальным данным. Поэтому на основе детерминированных
строятся локальные формальные модели с использованием мультипликативных
моделей. Такой подход вполне оправдан и, как показали результаты исследования,
носит универсальный характер и может быть использован при решении различного
рода задач математического моделирования и оптимизации ХТС.

230
10.2 Описание предлагаемого метода оптимизации
Оптимизация ХТС в условиях неопределенности вызывает необходимость
разрабатывать методы, позволяющие принимать решения с учетом этого
обстоятельства. В последние годы появились работы, в которых
рассматриваются методы решения подобного рода задач. В данной главе
предлагается приближенный метод решения задачи оптимизации ХТС в условиях
интервальной неопределенности параметров с использованием современных
программных продуктов. Работоспособность предложенного метода
иллюстрируется на примере оптимизации последовательности экстракторов с
рециклом в рамках системы компьютерной математики Mathcad.
Интервальное описание неточности информации предполагает естественную для
задач химической технологии ограниченность факторов и их представление
диапазоном возможных значений переменных.
Рассмотрим предлагаемый метод решения задачи оптимизации ХТС в условиях
неопределенности.
Выделим вектор неопределенных параметров Х=(х
1
,х
2
,…,х
m
)
Т
и вектор
оптимизирующих (управляющих) переменных U=(u
1
, u
2
,…,u
k
)
T
. Если задать
значения неопределенных и оптимизирующих параметров, то уравнения
математического описания позволяют вычислить сформулированный критерий
эффективности функционирования ХТС. На этой основе с учетом существующих
ограничений может быть построена функциональная зависимость критерия
оптимизации от оптимизирующих неопределенных параметров R = F(u
1
, u
2
,…u
k
,
x
1
, x
2
,…x
m
). Полученную таким образом функцию предлагается использовать на
следующем этапе для решения задачи оптимизации ХТС в условиях
интервальной неопределенности.
При реализации построенного таким образом вычислительного эксперимента
возникают следующие проблемы:
– определение числа точек вычислительного эксперимента;
– выбор численных значений неопределенных параметров и оптимизирующих
переменных;
– проведение многочисленных расчетов значений критерия оптимизации,
которые требуют многократного решения уравнений математического описания.
При решении задачи предлагается использовать известный подход для
построения модели для критерия оптимизации – метод Брандона.
При выборе численных значений неопределенных параметров и
оптимизирующих переменных можно использовать идеи планирования
эксперимента.
Так как для каждого неопределенного параметра и оптимизирующей переменной
заданы значения нижней и верхней границы, то с использованием случайных
чисел, равномерно распределенных на интервале [0;1], можно сгенерировать
дополнительно N векторных значений неопределенных параметров и
оптимизирующих переменных по формуле:
)xinfx(supslxinfx
iij,iij,i
,
)uinfu(supsluinfu
llj,llj,l
,
где sl
i,j
, sl
l,j
– случайные числа, равномерно распределенные на интервале [0;1],
i=1(1)m, l=1(1)k, j=1(1)N.
