Холоднов В.А. Системный анализ и принятие решений. Компьютерное моделирование и оптимизация объектов химической технологии в MathCad и Excel
Подождите немного. Документ загружается.

241
Given
W2
0.2
W3
0.2
W2
0.7
W3
0.7
x3
0
x3
0.05
W2
W3
x3
Maximize R1 W2 W3 x3( )
W2
W3
x3
0.2
0.2
0.045
R1 W2 W3 x3( ) 2.001
R2 G xf a W2 W3 x3( ) y3 2.5 x3 3.7 x3
2
113 x3
3
x3 0.1if
3.94 x3 29.6 x3
2
74 x3
3
otherwise
u1
G 1( ) x3 W3 y3
G 1( )
x2 u1 u1 0if
0.1 otherwise
y2 2.5 x2 3.7 x2
2
113 x2
3
x2 0.1if
3.94 x2 29.6 x2
2
74 x2
3
otherwise
u2
G 1( ) x2 W2 y2
G 1( )
x1 u2 u2 0if
0.1 otherwise
u3 G 1( ) x1 G xf
x4 u3 u3 0if
0.1 otherwise
y4 2.5 x4 3.7 x4
2
113 x4
3
x4 0.1if
3.94 x4 29.6 x4
2
74 x4
3
otherwise
u4
G 1( ) x3 G 1( ) x4[ ]
y4
W4 0.7 u4 0.7if
0.2 u4 0.2if
u4 otherwise
R2 G xf x4( ) a W2 W3 W4( )
R2 G xf a W2 W3 x3( ) 0.07

242
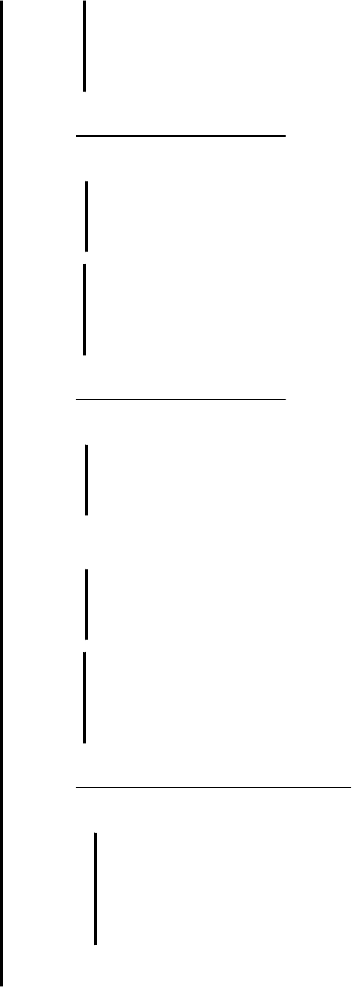
Ниже приведен протокол приближенного решения задачи оптимизации
Для этого вводятся вторые производные от критерия оптимизации по
управляющим переменным:
2
2
2
1
W
R
v
,
2
3
2
2
W
R
v
,
2
4
2
3
W
R
v
.
Критерий оптимизации представляется в следующем модифицированном виде:
RR
1модиф
,
где
2
3
2
2
2
1
vvvv .
f4 W2( ) 2.81 W2
2
3.26 W2
0.88
f2 xf( ) 27.54 xf
2
10.83 xf
1.1
G
1.
xf
0.2
a 0.05
W2
0.5
W3
0.3
W4
0.3
f1 G( ) 0.27 G
2
0.62 G
0.24
f3 a( ) 263.01 a
2
29.18 a
1.07
f5 W3( ) 9.19 W3
2
4.89 W3
6.12
f6 W4( ) 17.73 W4
2
14.80 W4
5.41
t1 W2 W3 W4( ) f4 W2( ) f5 W3( ) f6 W4( )( )
xf
R G xf a( )
d
d
t2 W2 W3 W4( ) f4 W2( ) f5 W3( ) f6 W4( )( )
a
R G xf a( )
d
d
t3 W2 W3 W4( ) f4 W2( ) f5 W3( ) f6 W4( )( )
G
R G xf a( )
d
d
t W2 W3 W4( ) t1 W2 W3 W4( )
2
t2 W2 W3 W4( )
2
t3 W2 W3 W4( )
2
R W2 W3 W4( ) R1 f4 W2( ) f5 W3( ) f6 W4( ) t W2 W3 W4( )
Given
W2
0.2
W3
0.2
W4
0.2
W2
0.7
W3
0.2
W4
0.7
W2
W3
W4
Maximize R W2 W3 W4( )
W2
W3
W4
0.2
0.2
0.2
R1 f4 W2( ) f5 W3( ) f6 W4( ) 0.077
R G xf a( ) 0.27 G
2
0.62 G 0.24
27.54 xf
2
10.83 xf 1.1
263.01 a
2
29.18 a 1.07
R1 0.27 G
2
0.62 G 0.24
27.54 xf
2
10.83 xf 1.1
263.01 a
2
29.18 a 1.07

243
Задача оптимизации – найти максимум R
модиф1
. Соответствующие значения
частных производных были рассчитаны по полученной аппроксимации критерия
оптимизации с помощью инструмента символьной математики Mathcad.
Результаты решения задачи представлены в нижеследующем протоколе.
Значения 0.11 и 0.418 в выражении для целевой функции представляют собой
маргинальные значения
,R , которые были найдены решением соответствующих
задач оптимизации.
Ниже приведен протокол решения задачи нахождения максимума R
модиф1
.
G
1
xf
0.2
a 0.05
W2
0.5
W3
0.336
W4
0.3
f1 G( ) 0.27 G
2
0.62 G
0.24
f2 xf( ) 27.54 xf
2
10.83 xf
1.1
f3 a( ) 263.01 a
2
29.18 a
1.07
f4 W2( ) 2.81 W2
2
3.26 W2
0.88
f5 W3( ) 9.19 W3
2
4.89 W3
6.12
f6 W4( ) 17.73 W4
2
14.80 W4
5.41
R1 0.27 G
2
0.62 G 0.24
27.54 xf
2
10.83 xf 1.1
263.01 a
2
29.18 a 1.07
R W2 W3 W4( ) R1 f4 W2( ) f5 W3( ) f6 W4( )
v1 W2 W3 W4( )
2
W2
R W2 W3 W4( )
d
d
2
W4
0.2
W2
0.7
W3
0.7
W4
0.7
W2
W3
W4
Maximize R W2 W3 W4( )
W2
W3
W4
0.2
0.7
0.417
v2 W2 W3 W4( )
2
W3
R W2 W3 W4( )
d
d
2
v3 W2 W3 W4( )
2
W4
R W2 W3 W4( )
d
d
2
Given
W2
0.2
W3
0.2
v W2 W3 W4( ) v1 W2 W3 W4( )
2
v2 W2 W3 W4( )
2
v3 W2 W3 W4( )
2
R W2 W3 W4( )
1
0.11
R1 f4 W2( ) f5 W3( ) f6 W4( )
1
0.418
v W2 W3 W4( )
244
Две последние строки в протоколе решения представляют соответственно
значения частных производных для оптимального значения управляющих
воздействий с учетом чувствительности и без её учета.
Найденное значение вектора управляющих воздействий W
T
=(0.2, 0.7, 0.417) дает
устойчивое значение критерия оптимизации по отношению к неточности
осуществления оптимального режима.
Предлагаемый метод позволяет также решать задачу поиска компромиссного
решения максимума дохода с его минимальной чувствительностью к
управляющим переменным и неопределенным параметрам. В этом случае
критерий оптимизации имеет следующий вид:
t)1(RR
2модиф
.
где – весовой коэффициент, учитывающий вклад того или иного показателя в
критерий оптимизации.
В следующем разделе представлены результаты решения задачи при значении
=0.5. Достоверность полученных результатов подтверждается совпадением
результатов, полученных с помощью Mathcad по точной модели (уравнения 10.1-
10.8) и приближенной модели (уравнение 10.9).
Найденное значение вектора управляющих воздействий W
T
=(0.2, 0.7, 0.2) дает
устойчивое значение критерия оптимизации по отношению к изменению
управляющих переменных и неопределенных параметров.
10.2.3 Стратегия минимакса для последовательности экстракторов с
рециклом
Для решения рассматриваемой задачи можно использовать стратегию
минимакса:
})x,...,x,x,u,...,u,u(Rmax{minR
Xx
k21k21
Uu
.
Это означает, что необходимо минимизировать максимальное значение дохода в
области изменения неопределенных параметров X.
Таким образом, сначала определяется максимум дохода в области X. При этом
убеждаются, что в этой области не существует его большего значения. Затем
находят такие значения управляющих переменных, при которых максимум дохода
принимает наименьшее значение в области допустимых решений.
Стратегию минимакса называют пессимистической, так как при этом подходе к
решению задачи всегда исходят из такой комбинации параметров, которая
максимально ухудшает значение дохода.
Ниже показан протокол решения задачи минимакса и полученные результаты.
R1 f4 W2( ) f5 W3( ) f6 W4( ) 0.064
v1 W2 W3 W4( )
2
0.064
v1 0.5 0.336 0.303( )
2
0.108
v2 0.5 0.336 0.303( )
2
0.083
v2 W2 W3 W4( )
2
0.054
v3 0.5 0.336 0.303( )
2
0.205
v3 W2 W3 W4( )
2
0.071
R W2 W3 W4( ) 0.128
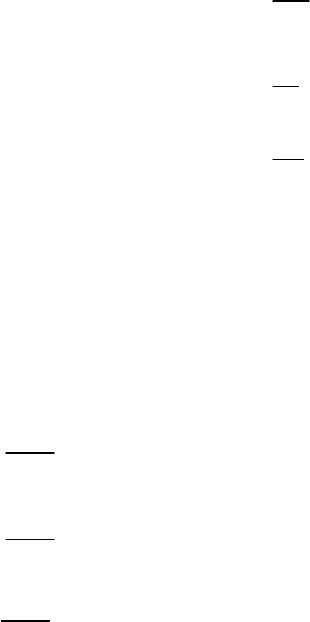
245
Результат решения задачи показывает, что отклонение дохода и управляющих
переменных относительно оптимальных значений сравнительно велики. Затраты
машинного времени на решение этой задачи сильно возрастают при усложнении
математической модели ХТС, увеличении числа параметров модели и
управляющих переменных.
G
1
xf
0.2
a 0.05
W2
0.5
W3
0.3
W4
0.3
1
1
2 1
1
f1 G( ) 0.27 G
2
0.62 G
0.24
f2 xf( ) 27.54 xf
2
10.83 xf
1.1
f3 a( ) 263.01 a
2
29.18 a
1.07
f4 W2( ) 2.81 W2
2
3.26 W2
0.88
f5 W3( ) 9.19 W3
2
4.89 W3
6.12
f6 W4( ) 17.73 W4
2
14.80 W4
5.41
R
G
xf
a
( )
0.27
G
2
0.62
G
0.24
27.54
xf
2
10.83
xf
1.1
263.01
a
2
29.18
a
1.07
t1 W2 W3 W4( ) f4 W2( ) f5 W3( ) f6 W4( )( )
xf
R G xf a( )
d
d
t2 W2 W3 W4( ) f4 W2( ) f5 W3( ) f6 W4( )( )
a
R G xf a( )
d
d
t3 W2 W3 W4( ) f4 W2( ) f5 W3( ) f6 W4( )( )
G
R G xf a( )
d
d
t W2 W3 W4( ) t1 W2 W3 W4( )
2
t2 W2 W3 W4( )
2
t3 W2 W3 W4( )
2
R1 0.27 G
2
0.62 G 0.24
27.54 xf
2
10.83 xf 1.1
263.01 a
2
29.18 a 1.07
R W2 W3 W4( ) R1 f4 W2( ) f5 W3( ) f6 W4( )
v1 W2 W3 W4( )
W2
R W2 W3 W4( )
d
d
v2 W2 W3 W4( )
W3
R W2 W3 W4( )
d
d
v3 W2 W3 W4( )
W4
R W2 W3 W4( )
d
d
246
Для охвата области допустимых значений неопределенных параметров
используется метод статистических испытаний с использованием чисел,
равномерно распределенных на интервале [0,1].
Ниже приведено решение задачи минимакса в рамках Mathcad.
v W2 W3 W4( ) v1 W2 W3 W4( )
2
v2 W2 W3 W4( )
2
v3 W2 W3 W4( )
2
R W2 W3 W4( ) R1 f4 W2( ) f5 W3( ) f6 W4( )
1 t W2 W3 W4( )
2 v W2 W3 W4(
)
Given
W2
0.2
W3
0.2
W4
0.2
W2
0.7
W3
0.7
W4
0.7
W2
W3
W4
Maximize R W2 W3 W4( )
W2
W3
W4
0.2
0.7
0.2
R1 f4 W2( ) f5 W3( ) f6 W4( ) 0.058

247
W2
0.5
W3
0.336
x3
0.04
R W2 W3 x3( ) y3 2.5 x3 3.7 x3
2
113 x3
3
x3 0.1if
3.94 x3 29.6 x3
2
74 x3
3
otherwise
N 10000
k rnd 1( )
l rnd 1( )
m rnd 1( )
G 0.8 k 0.4
xf 0.19 0.02 l
a 0.04 0.02 m
u1
G 1( ) x3 W3 y3
G 1( )
x2 u1 u1 0if
0.1 otherwise
y2 2.5 x2 3.7 x2
2
113 x2
3
x2 0.1if
3.94 x2 29.6 x2
2
74 x2
3
otherwise
u2
G 1( ) x2 W2 y2
G 1( )
x1 u2 u2 0if
0.1 otherwise
u3 G 1( ) x1 G xf
x4 u3 u3 0if
0.1 otherwise
y4 2.5 x4 3.7 x4
2
113 x4
3
x4 0.1if
3.94 x4 29.6 x4
2
74 x4
3
otherwise
u4
G 1( ) x3 G 1( ) x4[ ]
y4
W4 0.7 u4 0.7if
0.2 u4 0.2if
u4 otherwise
pr G xf x4( ) a W2 W3 W4( )
v
i
pr
i 1 N 1for
R
max
v
(
)
248
R W2 W3 x3( ) 0.115
Given
W2
0.2
W3
0.2
W2
0.7
W3
0.7
x3
0
x3
0.05
W2
W3
x3
Minimize R W2 W3 x3( )
W2
W3
x3
0.256
0.7
9.469 10
3
R W2 W3 x3( ) 0.084

249
11 Оптимизация ХТС в условиях вероятностной
неопределенности параметров
11.1 Постановка задачи
Одной из стратегий решения задачи оптимизации с учетом неопределенности
является стратегия нахождения экстремума математического ожидания целевой
функции F(u
1
,u
2,…
u
k
,x
1
,x
2
,…x
m
).
При использовании этой стратегии решается следующая задача:
))x,...,x,x,u,...,u,u(FM(extrZ
Xx
m21k21
Uu
,
где
m1
X
Xx
mm2211m21k21
Uu ,Xx
m21k21
dx...dx)x(p...)x(p)x(p)x,...,x,x,u,...,u,u(F...)}x,...,x,x,u,..,.u,u(F{M
p
1
(x
1
)…p
m
(x
m
) – функция распределения плотности вероятности неопределенных
параметров в виде случайных независимых величин x
1
…x
m
.
Обозначим:
ЦФM – математическое ожидание целевой функции;
ЦФ
– среднее квадратическое отклонение целевой функции;
ЦФ
– коэффициент вариабельности.
Тогда плотность распределения целевой функции при нормальном законе
распределения вычисляется по следующей зависимости:
)
2
)mx(
exp(
2
1
)ЦФ(f
2
2
,
где m = М[ЦФ] – математическое ожидание целевой функции;
=
ЦФ
– среднеквадратическое отклонение;
Функция распределения:
ЦФd)ЦФ(f)ЦФ(F
x
,
которая дает возможность определить вероятность появления случайной
величины ЦФ<а. График плотности распределения показывает, какие значения
случайной величины наиболее вероятны.
Вычисление многомерного интеграла связано с серьезными вычислительными
трудностями. Для их преодоления обычно используются метод Брандона –
построение приближенного значения целевой функции, метод Монте-Карло и на
перспективу рассматриваются вопросы распараллеливания вычислений. Как
правило, использование метода Монте-Карло имеет смысл при вычислении трех-,
четырехкратных и большей размерности интегралов.

250
11.2 Вычисление многомерных интегралов с помощью метода Монте-Карло
11.2.1 Основы метода Монте-Карло
Метод Монте-Карло - это статистический метод, его используют при вычислении
сложных интегралов, решении систем алгебраических уравнений высокого
порядка, моделировании поведения элементарных частиц, при исследовании
сложных систем (экономических, биологических и т. д.).
Сущность метода состоит в том, что в решаемую задачу вводят случайную
величину
, изменяющуюся по определенному закону Р(
). Как правило,
случайную величину выбирают таким образом, чтобы искомая в задаче величина
А стала математическим ожиданием
: М (
) = А.
Таким образом, мы определяем искомую величину А лишь теоретически. Для того
чтобы найти ее численно, пользуются статистическими методами: берут выборку
случайной величины
объемом N элементов. В результате получают N вариантов
случайной величины
i
, для которых вычисляют их среднее арифметическое
(выборочное среднее):
N
N
1i
i
,
которое и принимают в качестве приближенного значения искомой величины А:
А.
Для получения результата приемлемой точности по методу Монте-Карло
требуется большое число статистических испытаний. Именно поэтому этот метод
иногда так и называют – метод статистических испытаний.
11.2.2 Метод нахождения среднего значения функции для вычисления
n-мерного интеграла
Искомый интеграл запишется следующим образом:
G
n
n1n1
RG для ,dx...dx x,...,xfI
(11.1)
Причем область интегрирования G
n
R
, и G – ограниченное множество в
n
R
.
Следовательно, каждая точка x множества G имеет
n
координат:
n21
x,...,x,xx Gx .
От функции f(x) будем требовать, чтобы она была ограничена сверху и снизу на
множестве G:
21
n
21
C)x(fC , Gx , RC ,С
.
Пользуясь тем, что наше множество G ограниченное, впишем его в некоторый
параллелепипед K:
} Mxm , n,...,1i | Rx{K
iii
,n
,
где m
i
и M
i
– это нижние и верхние границы значений i-ой координаты множества
G:
i
Gx
ii
Gx
i
xmaxM ,xminm
.
