Холоднов В.А. Системный анализ и принятие решений. Компьютерное моделирование и оптимизация объектов химической технологии в MathCad и Excel
Подождите немного. Документ загружается.

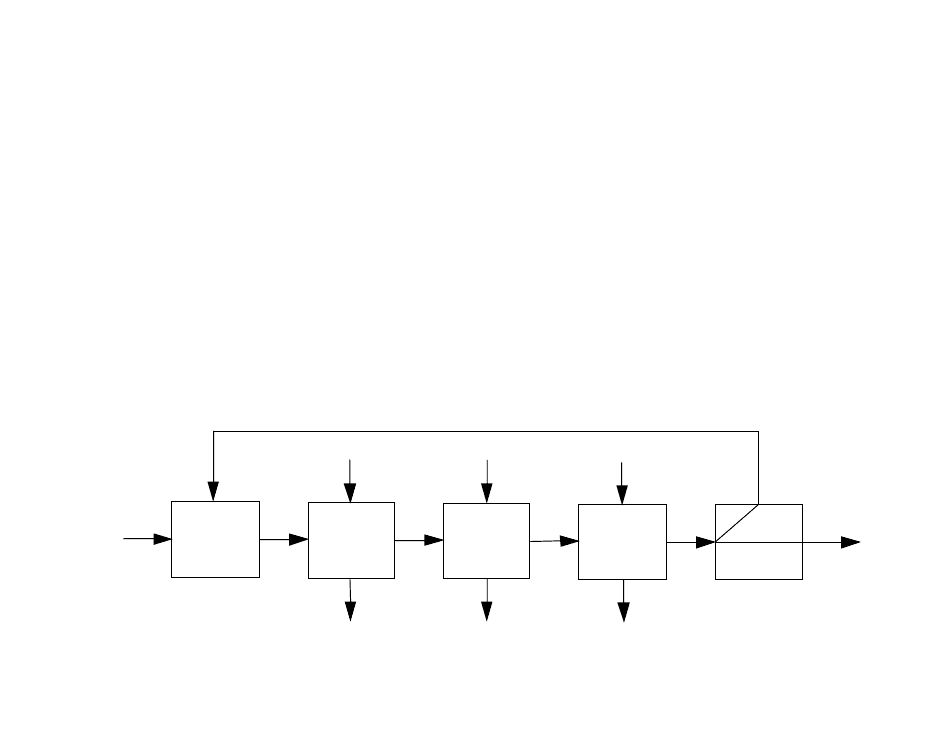
231
Предложенный и развитый нами метод оптимизации ХТС с учетом структуры
уравнений математического описания позволяет избежать многочисленных
расчетов.
10.2.1 Оптимизация каскада экстракторов с рециклом
В качестве объекта исследования рассматривается последовательность
экстракторов с рециклом, для которой решается задача оптимизации о
нахождении максимума дохода в условиях интервальной неопределенности.
В ХТС поступает сточная вода с определенным содержанием примеси, которая
извлекается в экстракторах 2, 3, 4 с помощью экстрагента. Часть не извлеченной
примеси возвращается на вход в систему.
Математическое описание рассматриваемой ХТС (Рисунок 10.1) представим в
виде уравнений материального баланса:
Рисунок 10.1 – Последовательность экстракторов с рециклом
14f
x)GGR(xGRxG
(10.1)
2221
x)GRG(yWx)GRG(
(10.2)
)x(fy
22
(10.3)
3332
x)GRG(yWx)GRG(
(10.4)
)x(fy
33
(10.5)
4443
x)GRG(yWx)GRG(
(10.6)
)x(fy
44
(10.7)
В качестве критерия оптимизации R принят доход от функционирования
установки:
)WWW(a)xx(GR
4324f
(10.8)
y
4
y
4
GR
W
2
W
3
W
4
x
4
x
4
G
y
4
x
4
x
3
x
2
x
1
x
f
G

232
Соотношения для уравнений равновесия между фазами экстракта и рафината
имеют вид:
0.1>x , x74x6.29x94.3
1.0x , x113x7.3x5.2
y
I
3
I
2
II
I
3
I
2
II
I
, I = 2,3,4
В уравнениях математического описания приняты следующие обозначения:
G, GR – расходы входного потока и потока рецикла,
час
кмоль
;
x
f
, x
I
, y
I
– концентрации извлекаемого вещества во входном потоке, в
соответствующем потоке экстракта и рафината, мольные доли;
W
2
, W
3
, W
4
– расходы экстрагента,
час
кмоль
;
a,
– стоимости растворителя и извлекаемого вещества a = 0.05,
= 1,
2.0x ,1GR ,1G
f
Ограничения на управляющие переменные 7.0W2.0
i
, i = 2, 3, 4.
Для решения этой типичной задачи химической технологии по оптимизации ХТС
существуют три традиционных метода:
– декомпозиция на структуре самой ХТС;
– декомпозиция на структуре уравнений математического описания ХТС;
– интегральный метод расчета.
Наиболее перспективным из них является метод, основанный на учете структуры
уравнений математического описания.
В соответствии с предлагаемым здесь алгоритмом в качестве оптимизирующих
приняты переменные W
2
, W
3
, x
3
. При таком выборе последовательность решения
уравнений и расчета неизвестных приведена в таблице 10.1. В этом случае
расчет ХТС на каждом шаге оптимизации осуществляется без итераций (рисунок
10.2).
Таблица 10.1 – Таблица связей
Исходная Преобразованная
Уравнения
Неизвестные, входящие
в уравнение
Уравнения
Выходные
переменные
10.1 x
4
, x
1
2.5 y
3
10.2 x
1
, W
2
, y
2
, x
2
2.4 x
2
10.3 x
2
, y
2
2.3 y
2
10.4 x
2
, W
3
, y
3
, x
3
2.2 x
1
10.5 x
3
, y
3
2.1 x
4
10.6 x
3
, W
4
, y
4
, x
4
2.7 y
4
10.7 x
4
, y
4
2.6 W
4
10.8 R, x
4
, W
2
, W
3
, W
4
2.8 R

233
Ниже представлен протокол решения задачи на основе учета структуры
уравнений.
Интегральный метод решения задачи оптимизации показан на рисунке 10.2.
Он основан на решении системы нелинейных алгебраических уравнений методом
Ньютона и при большом числе уравнений требует значительных затрат
машинного времени.
В связи с небольшой размерностью решаемой нами задачи вычислительный
эксперимент проводился по этой методике.
Вычислительный эксперимент осуществлялся по определенному плану (Таблица
10.2).
G
1
GR
1
xf
0.2
a 0.05
W2
0.5
W3
0.336
x3
0.057
f x( ) 2.5 x 3.7 x
2
113x
3
x 0.1if
3.94 x 29.6 x
2
74 x
3
otherwise
y3 f x3( )
x2
G GR( ) x3 W3 y3[ ]
G GR( )
y2 f x2( )
x1
G GR( ) x2 W2 y2[ ]
G GR( )
x4
G GR( ) x1 G xf[ ]
GR
y4 f x4( )
W4
G GR( ) x3 G GR( ) x4[ ]
y4
R G xf x4( ) a W2 W3 W4( )
y2 0.165
y3 0.134
y4 0.102
W4 0.303
x1 0.121
x2 0.079
x4 0.042
R 0.102
234
Таблица 10.2 – Исходные данные и результаты вычислительного эксперимента
Номер
вычислительного
эксперимента
G
X
f
a
W
2
W
3
W
4
R
расчет
R
аппроксимация
Относительная
погрешность, %
1 1.2 0.21 0.06 0.64 0.38 0.3 0.117 0.115 1.44
2 1.2 0.21 0.04 0.68 0.47 0.44
0.146 0.137 6.16
3 1.2 0.19 0.06 0.55 0.35 0.31
0.102 0.106 3.7
4 1.2 0.19 0.04 0.61 0.44 0.4 0.128 0.127 0.48
5 0.8 0.21 0.06 0.4 0.25 0.22
0.077 0.077 0.47
6 0.8 0.21 0.04 0.44 0.32 0.29
0.096 0.1 3.73
7 0.8 0.19 0.06 0.34 0.24 0.21
0.067 0.066 2.06
8 0.8 0.19 0.04 0.38 0.3 0.27
0.084 0.086 2.42
9 1 0.2 0.05 0.5 0.34 0.3 0.102 0.098 2.61
10 0.87
0.194 0.049 0.408 0.29 0.26
0.085 0.081 4.68
11 0.87
0.193 0.046 0.412 0.3 0.27
0.087 0.086 1.57
12 0.93
0.192 0.048 0.437 0.31 0.28
0.091 0.092 1.35
13 0.96
0.205 0.057 0.481 0.3 0.27
0.093 0.095 2.35
14 0.92
0.19 0.048 0.3 0.3 0.3 0.088 0.086 2.75
15 1.08
0.197 0.054 0.6 0.5 0.6 0.087 0.089 2.34
16 0.94
0.2 0.055 0.7 0.7 0.7 0.058 0.057 0.92
17 1.1 0.205 0.048 0.2 0.2 0.2 0.076 0.081 6.37
18 0.87
0.193 0.05 0.5 0.6 0.4 0.073 0.075 2.48
19 0.83
0.2 0.06 0.3 0.2 0.5 0.072 0.071 1.69
20 0.92
0.197 0.04 0.4 0.3 0.6 0.1 0.1 0.35
21 1 0.2 0.05 0.7 0.2 0.43
0.099 0.1 1
22 1 0.2 0.05 0.5 0.3 0.3 0.101 0.099 2.12
23 1 0.2 0.05 0.7 0.34 0.42
0.097 0.1 3.05
24 1 0.2 0.05 0.2 0.2 0.2 0.075 0.072 4.33
В качестве неопределенных параметров выбраны параметры, характеризующие
внешние условия: расход входного потока, концентрация извлекаемого вещества
во входном потоке и стоимость растворителя.

235
Первые восемь строк таблицы представляют собой результаты двухуровневого
плана вычислительного эксперимента, строка 9 – результаты решения задачи
оптимизации при средних значениях неопределенных параметров, строки с 10 по
24 – результаты решения задачи в случайных точках. Вычислительный
эксперимент производился с использованием программного продукта Mathcad.
Интервалы изменения численных значений неопределенных параметров
приведены в таблице 10.3.
Таблица 10.3 – Интервалы численных значений неопределенных параметров
G
x
f
a
Нижняя граница
0.8 0.19 0.04
Верхняя граница
1.2 0.21 0.06
Результаты решения задачи оптимизации в исходной точке (строка 9 таблицы
10.3) показаны на примере, приведенном выше и совпадают с известным из
литературы решением: x
1
= 0.121, x
2
= 0.079, x
3
= 0.057, x
4
= 0.041, y
2
= 0.166,
y
3
= 0.134, y
4
= 0.099, W
2
= 0.506, W
3
= 0.334, W
4
= 0.304, R = 0.102.
С помощью разработанной программы на основе метода Брандона и с учетом
ограничений на численные значения неопределенных параметров и
оптимизирующих переменных
2,3,4)i ,7.0W0.2 ,06.0a04.0 ,21.0x19.0 ,2.1G8.0(
if
была
получена аппроксимация критерия оптимизации (Рисунок 10.2) в следующем
виде:
)W(f)W(f)W(f)a(f)x(f)G(fR
4635243f21
(10.9)
G
1
GR
1
xf
0.2
a 0.05
W2
0.506
W3
0.334
W4
0.303
f x( ) 2.5 x 3.7 x
2
113x
3
x 0.1if
3.94 x 29.6 x
2
74 x
3
otherwise
x1 0.15
x2
0.1
x3 0.06
x4
0.02
y2
0.2
y3
0.3
y4
0.2
Given
G fx GR x4 GR G( ) x1
0
G GR( ) x1 W2 y2 G GR( ) x2
0
y2 f x2( )
0
G GR( ) x2 W3 y3 G GR( ) x3
0
y3 f x3( )
0
236
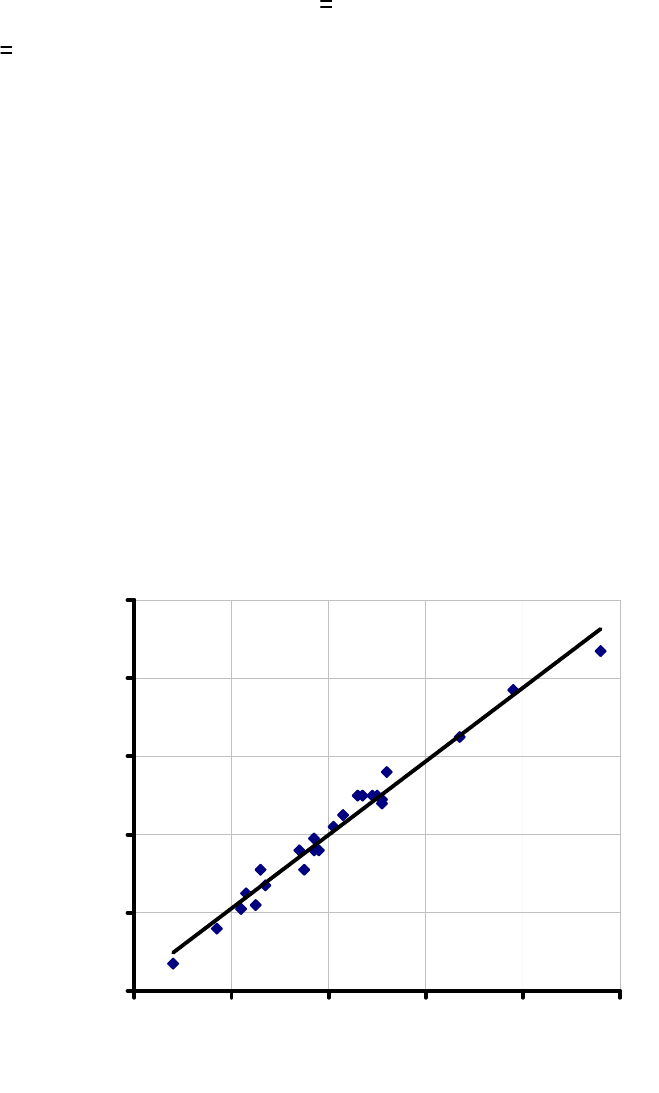
R=0.102
R
2
= 0,9766
0,05
0,07
0,09
0,11
0,13
0,15
0,05 0,07 0,09 0,11 0,13 0,15
Вычислительный эксперимент
Аппроксимация
Рисунок 10.2 – Результаты аппроксимации
Каждая из функций, входящих в уравнение (10.9), представляет собой полином
второй степени: f(x)=a
1
x
2
+a
2
x+a
3
. Численные значения коэффициентов для
соответствующих полиномов приведены в таблице 10.4.
G GR( ) x3 W4 f x4( ) G GR( ) x4
0
x1
0
x2
0
y4 f x4( )
0
y4
0
x3
0
x4
0
y2
0
y3
0
x1
x2
x3
x4
y2
y
y4
Find x1 x2 x3 x4 y2 y3 y4( )
x1
x2
x3
x4
y2
y3
y4
0.15
0.1
0.06
0.02
0.2
0.3
0.2
R G xf x4( ) a W2 W3 W4( )
237
Таблица 10.4 – Численные значения коэффициентов
Полином для переменной
1
a
2
a
3
a
f
1
(G) -0.27 0.62 -0.24
f
2
(x
f
) 27.54 -10.83 1.1
f
3
(a) 263.01 -29.18 1.07
f
4
(W
2
) -2.81 3.26 0.88
f
5
(W
3
) -9.19 4.89 6.12
f
6
(W
4
) -17.73 14.80 5.41
Ниже приведены результаты оптимизации, полученные с использованием
найденной на основе метода Брандона приближенной зависимости критерия
оптимизации от оптимизирующих переменных и неопределенных параметров.
Результаты приближенного нахождения максимума дохода совпадают с
результатами точного решения до 10-15%.
G
1.0
xf
0.2
a 0.05
W2
0.5
W3
0.33
W4
0.3
f1 G( ) 0.27 G
2
0.62 G
0.24
f2 xf( ) 27.54 xf
2
10.83 xf
1.1
f3 a( ) 263.01 a
2
29.18 a
1.07
f4 W2( ) 2.81 W2
2
3.26 W2
0.88
f5 W3( ) 9.19 W3
2
4.89 W3
6.12
f6 W4( ) 17.73 W4
2
14.80 W4
5.41
R 0.27 G
2
0.62 G 0.24
27.54 xf
2
10.83 xf 1.1
263.01 a
2
29.18 a 1.07
R1 W2 W3 W4( ) R f4 W2( ) f5 W3( ) f6 W4( )
R1 W2 W3 W4( ) 0.106
R1 W2 W3 W4( ) 0.11
Given
W2
0.2
W2
0.7
W3
0.2
W3
0.7
W4
0.2
W4
0.7
W2
W3
W4
Maximize R1 W2 W3 W4( )
W2
W3
W4
0.58
0.266
0.417

238
10.2.2 Решение задачи оптимизации для каскада экстракторов с рециклом с
использованием методов теории чувствительности
Для решения задачи оптимизации в условиях рассматриваемой
неопределенности воспользуемся чувствительностью критерия оптимизации по
соответствующим неопределенным параметрам:
G
R
t
1
,
f
2
x
R
t
,
a
R
t
3
.
С их помощью задача нахождения максимума дохода с его минимальной
чувствительностью по неопределенным параметрам была решена в системе
компьютерной математики Mathcad в соответствии с модифицированным
критерием:
tRR
модиф
,
где t=t
1
2
+t
2
2
+t
3
2
,
t – «штрафная» функция, которая уменьшает значение критерия
оптимизации при больших значениях чувствительности. Маргинальное значение
t = 0.
Задача оптимизации сводится к нахождению максимума R
модиф
по управляющим
переменным с минимальной чувствительностью найденного режима к
неопределенным параметрам. Соответствующие значения частных производных
были найдены по полученной аппроксимации критерия оптимизации с помощью
инструмента символьной математики Mathcad. Результаты решения задачи
представлены в нижеследующих примерах.
Достоверность полученных результатов подтверждается совпадением
результатов, полученных с помощью Mathcad по точной модели (уравнения 10.1-
10.8) и приближенной модели (уравнение 10.9).
Найденное значение вектора управляющих воздействий W
T
=(0.2, 0.2, 0.2) дает
относительно устойчивое значение критерия оптимизации по отношению к
изменению неопределенных параметров.
Предлагаемый метод позволяет решать задачу нахождения максимума дохода с
его минимальной чувствительностью к управляющим переменным, что позволяет
определить чувствительность критерия оптимизации к неточности осуществления
оптимального режима. Если некоторое отклонение от оптимального режима
приводит лишь к малым потерям, но зато удобно с технологической точки зрения,
то такое изменение режима может быть оправдано.
Ниже представлен протокол точного решения задачи оптимизации.
239
G
1.0
xf
0.2
a 0.05
W2
0.5
W3
0.33
x3 0.045
R G xf a( ) y3 2.5 x3 3.7 x3
2
113 x3
3
x3 0.1if
3.94 x3 29.6 x3
2
74 x3
3
otherwise
u1
G 1( ) x3 W3 y3
G 1( )
x2 u1 u1 0if
0.1 otherwise
y2 2.5 x2 3.7 x2
2
113 x2
3
x2 0.1if
3.94 x2 29.6 x2
2
74 x2
3
otherwise
u2
G 1( ) x2 W2 y2
G 1( )
x1 u2 u2 0if
0.1 otherwise
u3 G 1( ) x1 G xf
x4 u3 u3 0if
0.1 otherwise
y4 2.5 x4 3.7 x4
2
113 x4
3
x4 0.1if
3.94 x4 29.6 x4
2
74 x4
3
otherwise
u4
G 1( ) x3 G 1( ) x4[ ]
y4
W4 0.7 u4 0.7if
0.2 u4 0.2if
u4 otherwise
R G xf x4( ) a W2 W3 W4( )
240
R1 W2 W3 x3( ) y3 2.5 x3 3.7 x3
2
113 x3
3
x3 0.1if
3.94 x3 29.6 x3
2
74 x3
3
otherwise
u1
G 1( ) x3 W3 y3
G 1( )
x2 u1 u1 0if
0.1 otherwise
y2 2.5 x2 3.7 x2
2
113 x2
3
x2 0.1if
3.94 x2 29.6 x2
2
74 x2
3
otherwise
u2
G 1( ) x2 W2 y2
G 1( )
x1 u2 u2 0if
0.1 otherwise
u3 G 1( ) x1 G xf
x4 u3 u3 0if
0.1 otherwise
y4 2.5 x4 3.7 x4
2
113 x4
3
x4 0.1if
3.94 x4 29.6 x4
2
74 x4
3
otherwise
u4
G 1( ) x3 G 1( ) x4[ ]
y4
W4 0.7 u4 0.7if
0.2 u4 0.2if
u4 otherwise
t1
G
R G xf a( )
d
d
t2
xf
R G xf a( )
d
d
t3
a
R G xf a( )
d
d
t t1
2
t2
2
t3
2
R1 G xf x4( ) a W2 W3 W4( )
R1 R1 t
