Холоднов В.А. Системный анализ и принятие решений. Компьютерное моделирование и оптимизация объектов химической технологии в MathCad и Excel

Подождите немного. Документ загружается.

261

– предлагаемый метод предъявляет серьезные требования к точности

приближенной зависимости значения критерия оптимизации от неопределенных

параметров и оптимизирующих переменных;

– использование метода Монте-Карло упрощает получение точного решения

задачи, но связано с большими временными затратами.

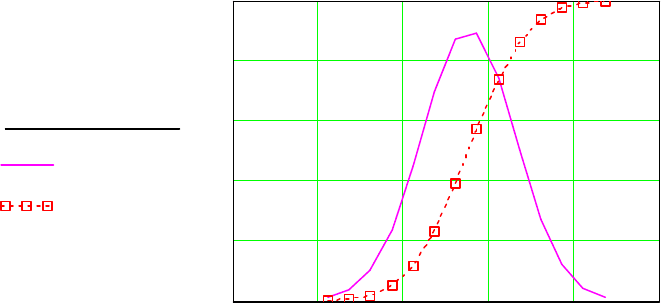
Рисунок 11.2 – Значения плотности распределения и функции распределения













Maximize R W2 W3 W4( )













0.58

0.266

0.417















R W2 W3 W4( ) 0.11



0.2





0.11

0.2



Rinf 0.11 3





Rsup 0.11 3





R Rinf Rinf 0.01

Rsup



F R( )





dnorm R 0.11





 







d

0 0.04 0.08 0.12 0.16 0.2

0.2

0.4

0.6

0.8

dnorm R 0.11





 

F R( )

262

12 Многоцелевая оптимизация

12.1 Основные понятия и определения

Многоцелевой (многокритериальной, векторной) оптимизацией принято называть

поиск оптимальных решений с учетом нескольких критериев качества .f,...,f,f

k21

Если рассматривается конечное число критериев качества, то говорят о

векторной оптимизации, поскольку значения частных (локальных) критериев

качества

f,...,f можно трактовать как компоненты вектора, имеющего

размерность k. Предполагается, что все частные критерии качества могут быть

оценены количественно.

Для решения задач многоцелевой оптимизации должны быть обеспечены

определенные условия. В частности, должна быть предоставлена возможность

изменять в определенных пределах независимые переменные ,x,...,x

влияющие

на критерии качества

f,...,f .

Любую независимую переменную величину

x , которую можно изменять в

некоторых пределах и которая оказывает определенное влияние на все критерии

качества или только на некоторые из них, принято называть управляемой

переменной (или управлением). Эта терминология в определенном смысле созвучна

терминологии из теории управления. Она подчеркивает, что процесс многоцелевой

оптимизации имеет сходство с процессом управления системой.

Совокупность всех управляемых переменных )x,...,x(

можно рассматривать как

вектор управления. Ему ставится в соответствие точка n-мерного пространства

управлений. Множество допустимых значений управляемых переменных

называется областью управления. Она характеризует ту часть пространства

управлений, где находятся все реализуемые управления. Эта область может

быть как связной, так, и несвязной. В частном случае она может состоять из

отдельных изолированных точек.

Пространство целей (или целевое пространство) – это k-мерное пространство,

координатами которого являются значения всех рассматриваемых критериев

качества

f,...,f .

Областью целей (или целевой областью) называется множество точек в

пространстве целей, где лежат все возможные значения векторов цели

)f,...,f(

. При этом каждой точке области целей соответствует одна или

несколько точек пространства управлений. Это значит, что один и тот же

результат (одна и та же целевая точка) может быть достигнут с помощью

различных комбинаций значений управляющих величин.

Эффективным множеством компромиссов называется множество всех целевых

точек, которые нельзя далее равномерно (т.е. одновременно по всем критериям)

улучшить в рамках имеющихся возможностей управления. Таким образом, к

этому множеству относятся все точки, несравнимые друг с другом в смысле

улучшения или ухудшения эффекта управления.

Как известно, скалярные величины можно легко упорядочить путем сравнения

их значений. Проблема сравнения векторных величин гораздо сложнее. Если

для этой цели воспользоваться «длиной» вектора (нормой), то по существу

задача сведется к сравнению скалярных величин. Если же при сравнении, как

это требуется в многоцелевой оптимизации, нужно сопоставлять отдельные

компоненты векторов, то сделать однозначное заключение возможно лишь

тогда, когда все без исключения компоненты одного вектора больше (или

меньше) соответствующих компонент другого вектора. Когда некоторые

компоненты одного вектора меньше, а остальные – больше соответствующих

компонент другого вектора, эти векторы считаются несравнимыми между

263

собой. Эта ситуация имеет место во множестве компромиссов. Вектор целей

)f,...,f(

равномерно лучше («больше») вектора )f,...,f(

, если

ff 

и если

существует, по крайней мере, одно

i , для которого

ff  . Совокупность всех

векторов целей, для которых в области целей не существует других равномерно

лучших векторов целей, образует эффективное множество компромиссов.

12.2 Компромиссные решения

При разработке новых процессов учитываются многочисленные качественные

показатели. Каждый из них стремятся оценить количественно с помощью

выбранного частного (локального) критерия оптимальности. Как правило, в

реальных задачах не удается достичь одновременно экстремальных значений всех

рассматриваемых критериев оптимальности, поскольку эти экстремумы

соответствуют различным точкам пространства независимых переменных

,x,...,x

варьируемых в процессе оптимизации.

Следовательно, решение задачи многокритериальной оптимизации представляет

собой некоторый компромисс между частными критериями оптимальности.

Обоснование принципа этого компромисса и составляет одну из основных

концептуальных трудностей проблемы векторной оптимизации.

Для наглядного представления компромиссных решений рассмотрим задачу

оптимизации с двумя критериями качества

f и

f . Если каждый из них является

непрерывной функцией независимых переменных ,x,...,x,x

n21

изменяющихся в

некоторой области пространства



, то существует не которая область



соответствующих значений частных критериев оптимальности (Рисунок 12.1).

Каждому набору частных критериев

f и

f соответствует определенная точка

области



. Точки области



делятся на улучшаемые и неулучшаемые.

Для определенности исходят из того, что желательно увеличить значение

каждого из рассматриваемых критериев. Если это не так, то знак

соответствующего критерия следует изменить на обратный. Анализ показывает,

что точки А и В внутри области возможных решений



(Рисунок 12.1). Очевидно, в

точке В оба критерия

f и

f имеют большие значения, чем в точке А.

Следовательно, решение задачи в точке В лучше, чем решение в точке А.

Процесс улучшения решений можно продолжить, двигаясь в том же направлении к

границе области



, где дальнейшее улучшение решений прекращается.

Максимальные значения критериев

f и

f достигаются в точках D и C

соответственно.

264

Рисунок 12.1 – Область возможных решений



и множество компромиссов CD

Точки, принадлежащие линии СD, обладают особым свойством: двигаясь вдоль

линии СD, нельзя улучшить

значение одного из критериев, не ухудшив при этом

значение другого критерия. В силу этого множество точек, образующих линию CD,

называют множеством компромиссных решений, или множеством компромиссов.

Решения, соответствующие множеству компромиссов, принято называть

эффективными.

Легко убедиться в том, что множеству компромиссов могут принадлежать лишь

точки на границе области



возможных решений; совокупность критериев,

соответствующих любой точке, лежащей внутри этой области, может быть

улучшена путем движения к границе.

Необходимым условием принадлежности точки множеству компромиссов при

максимизации обоих критериев (т. е.



max,



maх) является требование

того, чтобы касательная в соответствующей точке граничной кривой имела

отрицательный наклон. В качестве достаточного условия служит требование,

чтобы соответствующий участок области



нельзя было улучшить одновременно

по обоим критериям.

Рисунок 12.2 – Разновидности областей возможных решений и множеств

компромиссов



max

265

Отсюда следует, что, например, на рисунке 12.2 (а) отрезок границы между

точками А и В не принадлежит множеству компромиссов, поскольку его можно в

целом улучшить с помощью отрезка граничной кривой между точками С и D.

На рисунке 12.2 (б) множество компромиссов сводится к одной точке А,

поскольку оба критерия качества достигают в этой точке максимальных значений.

Надо отметить, что такой случай встречается крайне редко.

Участки границы области допустимых решений, параллельные осям координат

(Рисунок 12.2 (в)), не принадлежат множеству компромиссов, поскольку все

точки этих участков могут быть улучшены с помощью решений в точках А и В

соответственно. Если известна вся область допустимых решений, то чаще всего

можно сразу указать множество компромиссов. Очевидно, трудности возникают

тогда, когда область



нельзя описать аналитически и когда множество

компромиссов должно определяться поточечно с помощью методов поиска.

12.3 Основные критерии и задачи многоцелевой оптимизации

В общем виде задача многоцелевой оптимизации состоит в следующем.

Качество оптимизируемой системы оценивается k-мерной вектор-

функцией ))x(f),...,x(f),x(f()x(f

k21

 . Компоненты )x(f

вектор-функции )x(f

являются заданными вещественными функциями вектора )x,...,x(x

 . Компо-

ненты

x этого вектора представляют собой независимые переменные величины,

которые могут изменяться в установленных пределах. На эти переменные, как

правило, накладываются линейные или нелинейные ограничения. Возможности

изменения переменных x

следует рассматривать как ресурсы оптимизации. Вектор

х принадлежит, таким образом, множеству

его допустимых значений в

-мерном

евклидовом пространстве, т.е.





. Требуется найти точку





оптимизирующую в некотором смысле значения функций

f (x),

f..., (x). Так будет,

например, когда какое-то явление, объект или процесс рассматривается с различных

точек зрения и для формализации каждой точки зрения используется

соответствующая функция. Если явление рассматривается в динамике, поэтапно и

для оценки каждого этапа приходится вводить отдельную функцию, в этом случае

также приходится учитывать несколько функциональных показателей.

В зависимости от содержания задачи выбора эти функции называют критериями

оптимальности, критериями эффективности, целевыми функциями,

показателями или критериями качества.

Введенные термины можно проиллюстрировать рассмотрев задачу выбора

наилучшего проектного решения. В этой задаче множество

состоит из нескольких

конкурсных проектов (например, строительства нового предприятия), а критериями

оптимальности могут служить стоимость реализации проекта

и величина прибыли

f , которую обеспечит данное проектное решение (т.е. построенное предприятие).

Если ограничить рассмотрение данной задачи лишь одним критерием

оптимальности, практическая значимость решения такой задачи окажется

незначительной. В самом деле, при использовании только первого критерия будет

выбран самый дешевый проект, но его реализация может привести к недопустимо

малой прибыли. С другой стороны, на строительство самого прибыльного проекта,

выбранного на основе второго критерия оптимальности, может просто не хватить

имеющихся средств. Поэтому в данной задаче необходимо учитывать оба указанных

критерия одновременно. Если же дополнительно стараться минимизировать

нежелательные экологические последствия строительства и функционирования

предприятия, то к двум указанным следует добавить еще один – третий критерий и

т.д. Что касается лица, принимающего решение (ЛПР), осуществляющего выбор

266

проекта, то в данной задаче таковым является глава администрации района, на

территории которого будет построено предприятие, при условии, что это

предприятие является государственным. Если же предприятие – частное, то в

качестве ЛПР выступает глава соответствующей фирмы.

С помощью векторного критерия лишь намечаются определенные цели, которые

нередко оказываются весьма противоречивыми. Эти цели одновременно, как

правило, достигнуты быть не могут, и поэтому речь может идти о компромиссном

решении.

Задачу векторной оптимизации можно сформулировать следующим образом:

Найти

– минимум целевых функций

)x...,x,x(f),.....,x...,x,x(f),x...,x,x(f

n,21mn,212n,211

– максимум целевых функций

)x...,x,x(f),..,x...,x,x(f),x...,x,x(f

n,21Mn,212mn,211m 

по поисковым переменным

n,21

x...,x,x

при наличии ограничений:

– на поисковые переменные

lll

xsupxxinf  , n)1(1i



;

– число поисковых переменных;

– на поисковые переменные в виде функциональных неравенств

0)x,..,x,x(G

n21j

 , J)1(1j



;

J – число функциональных неравенств;

– на поисковые переменные в виде функциональных равенств

0)x,...,x,x(H

n21i

 , I)1(1i



;

– число функциональных равенств.

Для сравнения критериев, имеющих разный физический смысл (и естественно

разные размерности), проводят нормализацию критериев в следующем виде:

для целевых функций )x...,x,x(f),.....,x...,x,x(f),x...,x,x(f

n,21mn,212n,211

)ff(

мин,iмакс,i

мин,ii





, m)1(1i



;

для целевых функций

)x...,x,x(f),..,x...,x,x(f),x...,x,x(f

n,21Mn,212mn,211m 

)ff(

мин,iмакс,i

iмакс,i





M),...2m(),1m(i





267

Эти функции

D сглаживают поверхность значений

и являются монотонными.

Кроме того, значения ]1,0[D

 , что обеспечивает инвариантность к масштабу

изменения критериев. Это позволяет сформулировать задачу многокритериальной

оптимизации в следующем виде:

Найти минимум целевых функций

)x...,x,x(D),.....,x...,x,x(D),x...,x,x(D

n,21Mn,212n,211

по поисковым переменным

n,21

x...,x,x при наличии ограничений:

– на поисковые переменные

lll

xsupxxinf  , n)1(1i



;

– число поисковых переменных;

– на поисковые переменные в виде функциональных неравенств

0)x,..,x,x(G

n21j

 , J)1(1j



;

J – число функциональных неравенств;

– на поисковые переменные в виде функциональных равенств

0)x,...,x,x(H

n21i

 , I)1(1i



;

– число функциональных равенств.

В зависимости от того, в каком виде проявляется действие различных критериев,

задачи многоцелевой оптимизации можно разделить на несколько классов.

Задачи многоцелевой оптимизации делят на статические и динамические.

Статическая задача – поиск управления

x,...,x в виде констант, оптимальных с

точки зрения заданных критериев качества ).k...2,1i(),x,...,x,x(f

n21i



Динамическая задача – поиск функций времени ),t(x),...,t(x

оптимальных

относительно критериев ).k,...,2,1i()),t(x),...,t(x(f

n1i



Значительное количество многокритериальных задач представляет собой

расширение и обобщение однокритериальных. При технико-экономической

оптимизации встречаются, например, задачи многоцелевого линейного

программирования. Другая распространенная задача – это задача многоцеле-

вого нелинейного программирования.

В процессе векторной оптимизации при одновременном использовании

критериев они тем или иным способом объединяются в один составной

критерий, который затем максимизируется (или минимизируется).

В некоторых задачах многоцелевой оптимизации локальные критерии имеют

различную физическую природу, а потому и различную размерность. В

многоцелевой оптимизации находит применение операция нормирования

локальных критериев, с помощью которой вместо «натурального» критерия

вводится его отношение к некоторой нормирующей величине, измеряемой в

тех же единицах, что и сам критерий. В результате такой операции все

частные (локальные) критерии приобретают безразмерный вид.

На практике используются различные варианты критериев при векторной

оптимизации. Например, обобщенный критерий может представлять собой

268

сумму нормированных частных критериев:







maxDR . Его называют

аддитивным критерием оптимальности. Наилучшее решение соответствует

максимуму аддитивного критерия оптимальности. В большинстве задач

векторной оптимизации частные критерии имеют различную важность. При

формировании обобщенного аддитивного критерия это учитывается с помощью

весовых коэффициентов ,



которые иногда называют коэффициентами

важности:









;







Обычно значения



определяются с помощью экспертной оценки (см. раздел

12.3.1).

Иногда обобщенный критерий оптимальности записывают в виде произведения

нормированных частных критериев:





DR или ,DR







где



– весовые коэффициенты важности. Такой критерий принято называть

мультипликативным.

Если все частные критерии нормированы к единице, т. е. 1D0

 , то удобно

использовать мультипликативный критерий в виде:



















или





















Нетрудно заметить, что в этом случае, 1R0



следовательно, обобщенный

критерий изменяется в том же диапазоне, что и частные критерии.

Как аддитивный, так и мультипликативный критерий имеют один недостаток:

малое значение одного частного критерия может быть компенсировано за счет

большого значения другого. Для уменьшения влияния этого недостатка

обычно вводятся ограничения на минимальные значения частных критериев

оптимальности.

При решении задач многоцелевой оптимизации наряду с нахождением

компромиссного решения иногда ищут также экстремальные решения,

получаемые при попытках оптимизировать какой-либо частный критерий

оптимальности )x(f



. Такие решения n,...,2,1i,x

 называются

маргинальными, или локально-оптимальными.

Решение многокритериальной задачи оптимизации на основе маргинальных

решений заключается в следующем.

Сначала отыскиваются маргинальные решения для k-целевых функций:

)k)1(1i(),(f

 . На втором этапе составляется обобщенный критерий

оптимальности в следующем виде:

 







iim

)(f)(fR или

iim

)(f

)(f)(f





















 ,

iim

)(f

)(f)(f

























– весовые коэффициенты.

269

12.3.1 Определение коэффициентов веса параметров

Важным элементом при исследовании (в данном случае маркетинговом)

любого процесса является назначение коэффициентов веса каждого фактора.

Распространенный метод – определение коэффициентов веса с помощью

экспертов, который представляет собой, по существу, обычное обсуждение с

той лишь разницей, что свое мнение эксперты выражают не словами, а

цифрами. Для определения влияния коэффициентов веса на результат

решения задачи можно решать ее при различных значениях этих

коэффициентов.

Существует достаточно много методов определения экспертных оценок,

сущность которых рассматривается ниже.

При непосредственном назначении коэффициентов веса i-тый эксперт

оценивает сравнительную важность рассматриваемых параметров, которые

будут входить в целевую функцию. В этом методе каждый i-ый эксперт для

каждого k-гo параметра должен назначить коэффициент веса



таким

образом, чтобы сумма всех коэффициентов веса, назначенных одним

экспертом для различных параметров, равнялась единице. Это требование

можно записать так:





1W , n,1i  , где n – число экспертов.

Согласованность экспертов определяется следующим образом:

1. Определяется число исследуемых факторов k.

2. Создается базовая таблица (см. Таблицу 12.1).

Таблица 12.1 – Базовая таблица

Факторы

Эксперт

A B C

Сумма

1 0.5 0.2 0.3 1.0

2 0.5 0.3 0.2 1.0

3 0.2 0.4 0.4 1.0

4 0.2 0.3 0.5 1.0

5 0.4 0.2 0.4 1.0

6 0.3 0.4 0.3 1.0

7 0.3 0.3 0.4 1.0

8 0.5 0.2 0.3 1.0

Среднее значение

коэффицие

та веса

0.363 0.288 0.35

Среднее квадратичное

отклонение

0,119 0,049 0,06

270

3. Рассчитывается среднее арифметическое значение коэффициента веса для

любого эксперта j (j=1(1)N) для любого параметра i (i=1(1)k) по формуле:







jiсреднее,j

4. Оценивается среднее квадратичное отклонение для каждого коэффициента

веса:











.средн,jji

)YY(

5. Определяется коэффициент вариабельности (v) = среднее квадратичное

отклонение / среднее значение коэффициента веса.

Значение коэффициента вариабельности показывает величину

разброса экспертных оценок. При v < 0,2 оценки экспертов можно считать

согласованными. В случае v > 0,2 целесообразно провести с экспертами

содержательное обсуждение важности оцениваемых параметров, после чего

повторить экспертизу. При сохранении величины разброса целесообразно

учитывать вероятностный характер экспертных оценок по методам,

приведенным ниже.

Как показывает опыт, удовлетворение экспертами требования





1W ,

n,1i  , где n – число экспертов при к > 3, вызывает затруднение.

Для того чтобы избежать выполнения этого требования, можно

коэффициенты веса определять и другими методами, рассмотренными ниже.

12.3.2 Оценка важности параметров в баллах

При оценке важности факторов в баллах каждый эксперт оценивает их,

например, по десятибалльной системе. При этом оценка, назначаемая

экспертом одному из факторов, не связана с оценками, которые он

назначает другим факторам. Например, всем факторам можно назначать

одинаковую оценку. Определение экспертных оценок в баллах производится

по следующему алгоритму.

1. Сформировать таблицу по форме, в которую вносятся оценки всех

факторов в баллах, сделанные каждым экспертом (см. Таблицу 12.2).

2. Перейти от оценок факторов в баллах к значениям коэффициентов веса,

сумма которых для всех факторов равна единице у каждого эксперта.

3. Определить коэффициент вариабельности.