Холоднов В.А. Системный анализ и принятие решений. Компьютерное моделирование и оптимизация объектов химической технологии в MathCad и Excel
Подождите немного. Документ загружается.

271
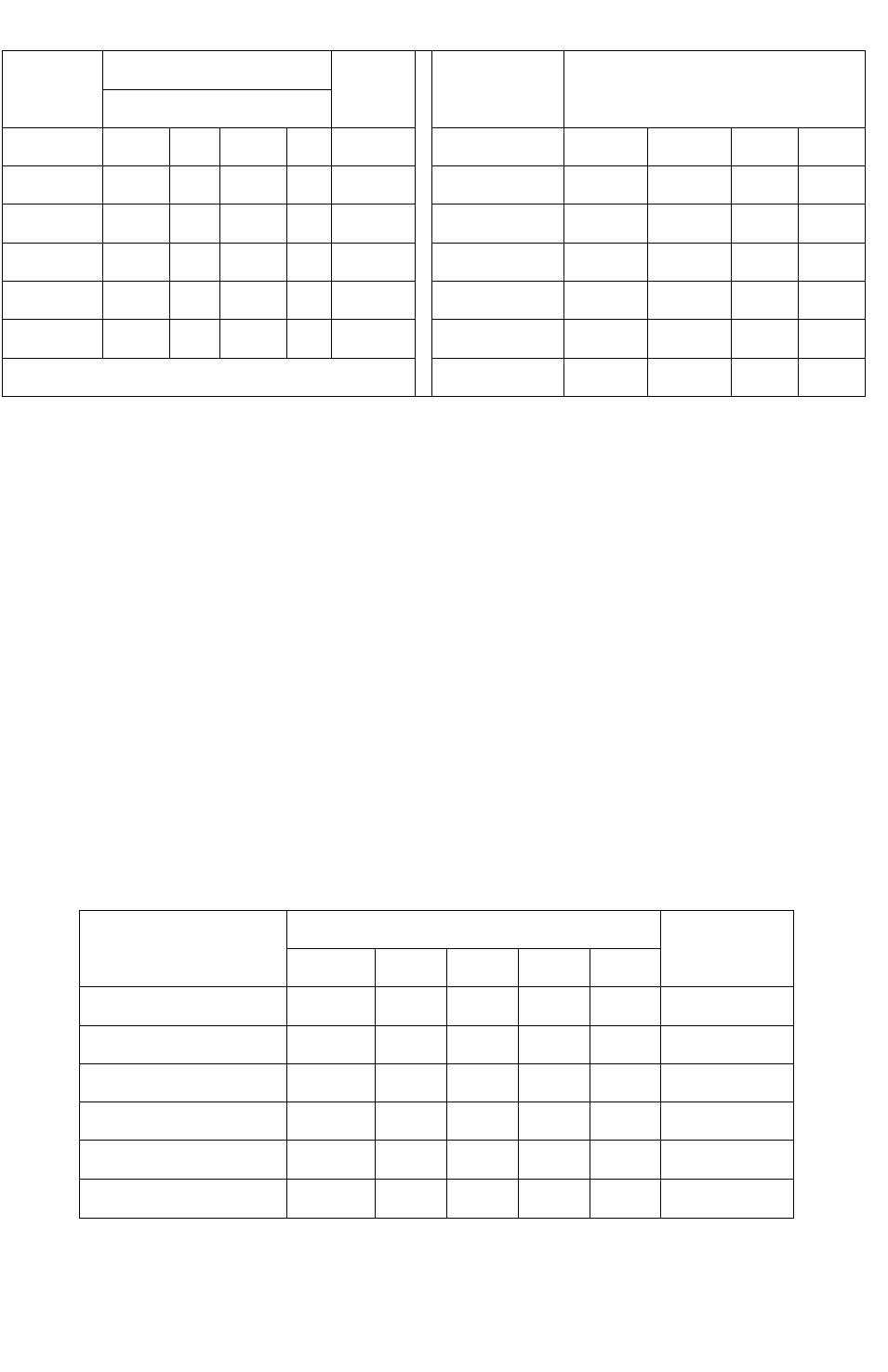
Таблица 12.2 – Базовая таблица с оценками всех факторов в баллах
Оценка в баллах
Эксперт
Факторы
Сумма
Эксперт Факторы
A Б В Г А Б В Г
1 6 7 5 7 25 1 0.24 0.28 0.20
0.28
2 10 8 4 9 31 2 0.32 0.26 0.13
0.29
3 5 7 6 8 26 3 0.19 0.27 0.23
0.31
4 7 9 5 7 28 4 0.25 0.32 0.18
0.25
5 8 6 4 6 24 5 0.33 0.25 0.17
0.25
Коэф. веса
0.27 0.28 0.18
0.28
12.3.3 Метод парных сравнений
Если при k > 3 одновременная оценка всех факторов вызывает затруднения,
их можно оценивать еще одним методом, который называется методом
парных сравнений. Этот метод реализуется с помощью следующего
алгоритма:
1. Определить число оцениваемых факторов k и число экспертов n.
Пусть k = 5; n = 4.
2. Для каждого эксперта составить отдельную таблицу (см. Таблицу 12.3).
В этой таблице эксперт должен ввести оценку парных сравнений, которая
заключается в следующем.
Если k-ый параметр важнее j-гo, то в ячейке, принадлежащей k-ой строке и j-
му столбцу, указывается 1, иначе – 0.
Пример заполнения такой таблицы первым экспертом приведен ниже, из нее
видно, что по оценке этого эксперта параметр А менее важен, чем
параметры Б и Д, но более важен, чем В и Г.
Таблица 12.3 – Базовая таблица с оценкой парных сравнений для 1-го эксперта
Параметры
Параметры
А Б В Г Д
Сумма
А ▲ 0 1 1 0 2
Б 1 ▲ 0 1 0 2
В 0 1 ▲ 0 0 1
Г 0 0 1 ▲ 1 2
Д 1 1 1 0 ▲ 3
10
Далее переходим к таблице с указанием веса каждого параметра
(см. Таблицу 12.4).

272
Таблица 12.4 – Результаты сравнений
Факторы Сумма
Эксперт
А Б В Г Д
1 0.2 0.2 0.1 0.2 0.3 1
… … … … … … …
Коэфф. веса
12.3.4 Функция желательности
Одним из наиболее удачных способов решения задачи оптимизации процессов
с большим количеством откликов (критериев), является использование
предложенной Харрингтоном в качестве обобщенного критерия оптимизации так
называемой обобщенной функции желательности D. Для ее построения
предлагается преобразовать измеренные значения критериев в безразмерную
шкалу желательности d. Построение шкалы желательности, которая
устанавливает соотношение между значением критерия у и соответствующим
ему значением d (частной функцией желательности), является в своей основе
субъективным, отражающим отношение эксперта к отдельным критериям. Для
построения шкалы желательности удобно использовать метод
количественных оценок с интервалом значений желательности от нуля до
единицы, хотя возможны и другие варианты шкалы. Значение d=0 (или D=0)
соответствует абсолютно неприемлемому значению критерия; а d=1 (D=1) –
самому лучшему значению. Промежуточные значения желательности и
соответствующие им числовые отметки приведены в таблице 12.5.
Таблица 12.5 – Базовые отметки шкалы желательности
Количественная отметка на шкале
желательности
Желательность
значения отклика
0.8÷1.00
Очень хорошо
0.63÷0.8
Хорошо
0.37÷0.63
Удовлетворительно
0.2÷0.37
Плохо
0.0÷0.2
Очень плохо
Такой выбор числовых отметок объясняется удобством вычислений, поскольку
)1exp(
1
163.0d , а
)1exp(
1
37.0d , e = 2.71828.
Построенная в соответствии с таблицей шкала d, представляет собой
безразмерную шкалу, при помощи которой любой критерий может быть
преобразован так, чтобы его можно было интерпретировать в терминах
полезности или желательности для любого специфического применения.
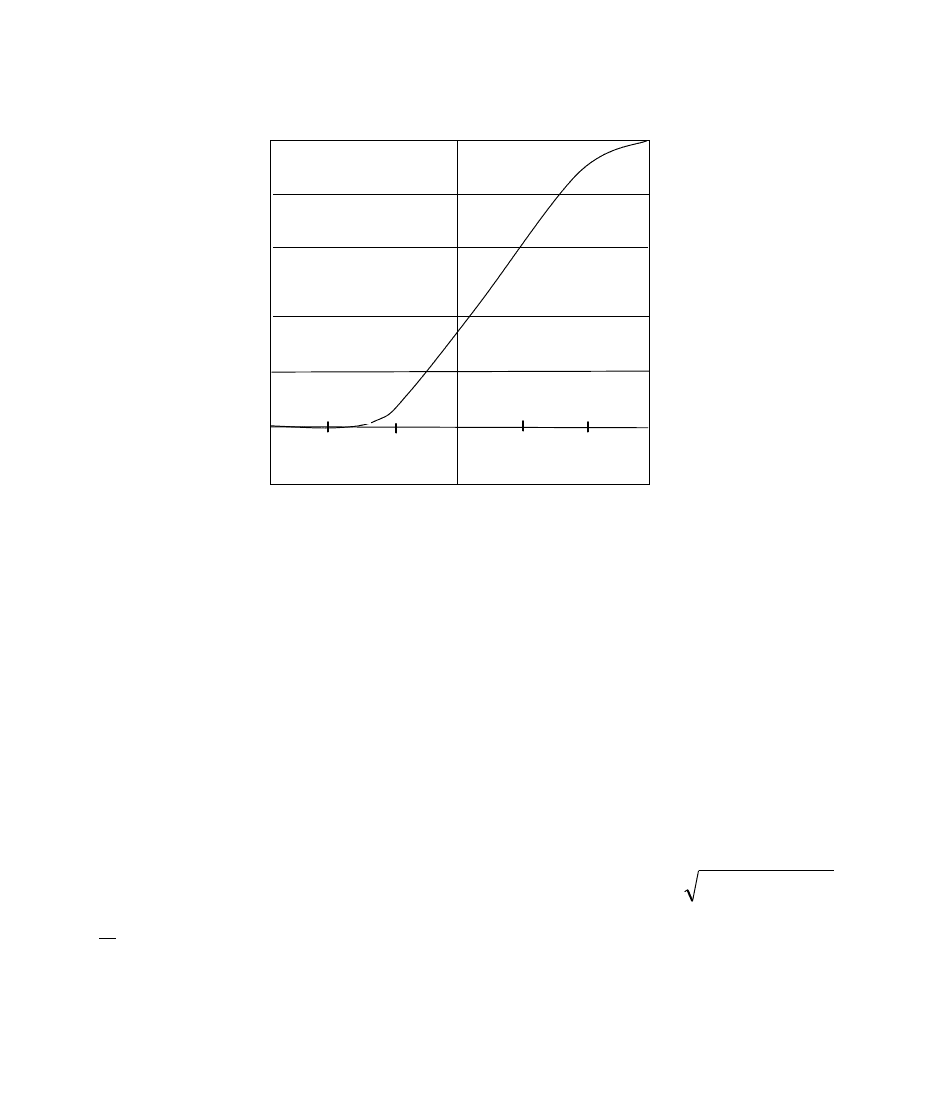
273
Для односторонних ограничений вида
max
yy или
min
yy более удобной
формой преобразования y в d служит другая экспоненциальная зависимость
(Рисунок 12.3):
)yexp(expd
c
Рисунок 12.3 – График преобразования
В формуле ybby
10c
коэффициенты
10
b,b можно определить, если задать
для нескольких значений свойства у соответствующие значения желательности d
(предпочтительно в интервале 0,2 < d < 0,8).
Имея несколько критериев, преобразованных в шкалу d, можно при помощи
арифметических операций скомбинировать некий обобщенный показатель
желательности D. При этом, если какой-либо один отклик является абсолютно
неудовлетворительным, обобщенная функция желательности D должна быть
равна 0 независимо от уровня остальных критериев. Математическим
выражением, отвечающим этим требованиям, служит среднее геометрическое
частных функций желательности, т.е.
k
k21
d...ddD или
))d...ddln(
k
1
exp(D
k21
. Очевидно, что если какое-либо одно
i
d =0, то
соответствующее D=0. Более того, на D сильно влияют именно наименьшие
значения
i
d . В то же время D=1 только тогда, когда все частные желательности
i
d =1. С обобщенной функцией желательности D можно производить все
вычислительные операции, как и с любым критерием системы, можно
использовать D в роли критерия оптимизации в маркетинговых исследованиях.
12.3.5 Метод нечетких множеств
12.3.5.1 Основы метода
В обычной теории множеств существует понятие множества как совокупности
элементов, обладающих определенным свойством или набором свойств. Обычно
обозначают множества строчными буквами, а их элементы – прописными. Тогда
принадлежность элемента и множеству U запишется следующим образом: и
U
очень хорошее
хорошее
удовлетвори-
тельное
плохое
очень
плохое
y
’
y
2
1
0
-1
-2
-3
y
min (max)
274
Таким образом, в обычной теории множеств принята бинарная классификация
элементов с точки зрения их принадлежности к рассматриваемому множеству.
Элемент может либо принадлежать множеству, либо не принадлежать ему,
третьего не дано.
Теория нечетких множеств, основоположником которой является Л. А. Заде,
раздвинула границы понятия принадлежности элемента множеству. Согласно
этой теории, элемент может принадлежать множеству не только полностью, но и
частично.
В теории множеств используется понятие универсального множества. Под
универсальным множеством понимают всю совокупность элементов, образующих
его. Эта совокупность может быть конечной или бесконечной. Так, если при
проведении технологического процесса концентрация реагента может принимать
только пять фиксированных значений: 2, 4, 8, 16 и 32%, то их можно рассматри-
вать в качестве элементов некоторого универсального множества. Обозначим эти
элементы буквами: 32u,16u,8u,4u,2u
54321
. Данное универсальное
множество можно представить в следующем виде:
54321
u,u,u,u,uU .
В теории нечетких множеств используется следующая форма записи:
5
1
i54321
uuuuuuU .
Здесь знак суммирования обозначает операцию не арифметического
суммирования, а объединения всех элементов u
i
(i=1, п) в одно множество U.
Если значения температуры в технологическом процессе непрерывно изменяются
и лежат в диапазоне [T
1
,T
2
], то, с точки зрения теории нечетких множеств, в
качестве универсального множества может быть принят этот диапазон тем-
ператур. Очевидно, в данном случае универсальное множество содержит
бесконечное количество элементов.
Всякое нечеткое подмножество А универсального множества U определяется
функцией принадлежности
A
, которая ставит в соответствие каждому элементу
и
U число из интервала [0,1], характеризующее степень принадлежности
элемента и подмножеству А. Эту формулировку можно представить в виде
следующей записи:
A
: U
0,1
Форма представления нечеткого множества А универсального множества U имеет
вид: A=
1
/u
1
+
2
/u
2
+…+
n
/u
n
=
n
/u
n
. Здесь (
I
– значение степени принадлежности,
т.е. число в диапазоне от 0 до 1, характеризующее принадлежность элемента
и
i
U нечеткому подмножеству А универсального множества U. Наклонная черта
отделяет значение степени принадлежности от элемента u
i
, который она харак-
теризует, а знак суммирования обозначает объединение элементов.
Пусть, например, имеется универсальное множество U, содержащее пять
элементов в виде чисел: 0, 20, 40, 60, 100. Построим на его базе нечеткое
подмножество А, характеризующееся следующими значениями степени
принадлежности:
u
i
, 0 20 40 60 100
i
1 0.8 0.5 0.2 0
Тогда подмножество А можно записать в следующем виде:
A=1/0+0.8/20+0.5/40+0.2/60+0/100
275
Рассмотрение нечеткого подмножества А как составной части некоторого
универсального множества U вытекает из следующего. Как уже отмечалось, в
теории обычных множеств введено понятие характеристического числа (индика-
тора). Используя это понятие и форму записи нечеткого множества, можно
представить универсальное множество U в следующем виде: U=1/и
1
+1/и
2
+ ...
+1/u
n
. В этом выражении степень принадлежности
i
всех элементов ui множеству
U равна 1.
Если элемент нечеткого множества обладает только одним единственным
свойством, то он характеризуется одной функцией принадлежности. Если же он
имеет несколько свойств, то каждому из них соответствует своя отдельная
функция принадлежности.
12.3.5.2 Операции над нечеткими множествами
Рассмотрим основные операции, выполняемые над нечеткими множествами. Для
множеств установлены следующие теоретико-множественные отношения:
отношение равенства множеств А и В. В случае нечетких множеств А и B
отношение равенства A=В имеет место тогда и только тогда, когда для любого
элемента и
i
U имеет место
A
(u)=
B
(u) , т.е. отношение равенства выполняется
при равенстве функций принадлежности соответствующих нечетких множеств
универсального множества U.
Объединение нечетких множеств A и В обозначается А+В (или A
В) и
определяется следующим образом: С=A+В=A
В
(
C
(u)=max(
A
(u),
B
(u)). Эта
операция обозначает нахождение наибольшего числа из двух чисел
B
(u)
и
A
(u)
при каждом фиксированном элементе и
U .
В качестве примера в таблице 12.6 представлена реализация операции
объединения нечетких подмножеств А и В универсального множества U.
Эту операцию можно также представить в виде следующих записей:
50
1
40
8.0
30
6.0
20
3.0
10
0
A ;
50
2.0
40
3.0
30
9.0
20
8.0
10
2.0
B ;
50
1
40
7.0
30
9.0
20
8.0
10
2.0
BAC .
Таблица 12.6 – Операция объединения нечетких подмножеств
U 10 20 30 40 50 60
A
(u)
0 0.3 0.6 0.7 1.0 0.9
B
(u)
0.2 0.8 0.9 0.3 0.2 0.1
C
(u)
0.2 0.8 0.9 0.7 1.0 0.9

276
Рисунок 12.4 – Операция объединения нечетких подмножеств:
а – исходные функции степеней принадлежности;
б – результирующая функция степени принадлежности
На рисунке 12.4 представлена графическая реализация операции объединения
нечетких подмножеств Р и Q универсального множества U.
Пересечение нечетких подмножеств А и В универсального множества U
определяется следующим образом: С=А
В
(
C
(u)
= min(
A
(u),
B
(u)
). Эта
операция обозначает нахождение наименьшего числа из двух чисел
A
(u),
B
(u)
при каждом фиксированном и
U .В качестве примера в таблице 12.7
представлена реализация операции пересечения нечетких подмножеств A и B
универсального множества U.
Таблица 12.7 – Операция пересечения нечетких подмножеств
U 20 40 60 80 90 100
A
(u)
0.1
0.3
0.5
0.7
0.9
1
B
(u)
0.2
0.5
1.0
0.6
0.5
0.4
C
(u)
0.1
0.3
0.5
0.6
0.5
0.4
Эту операцию можно также представить в виде следующих записей:
100
1
80
7.0
60
5.0
40
3.0
20
1.0
A ;
100
4.0
80
6.0
60
1
40
5.0
20
2.0
B ;
100
4.0
80
6.0
60
5.0
40
3.0
20
1.0
C .
б
P
U
C
0
0
а
1
1
u
u
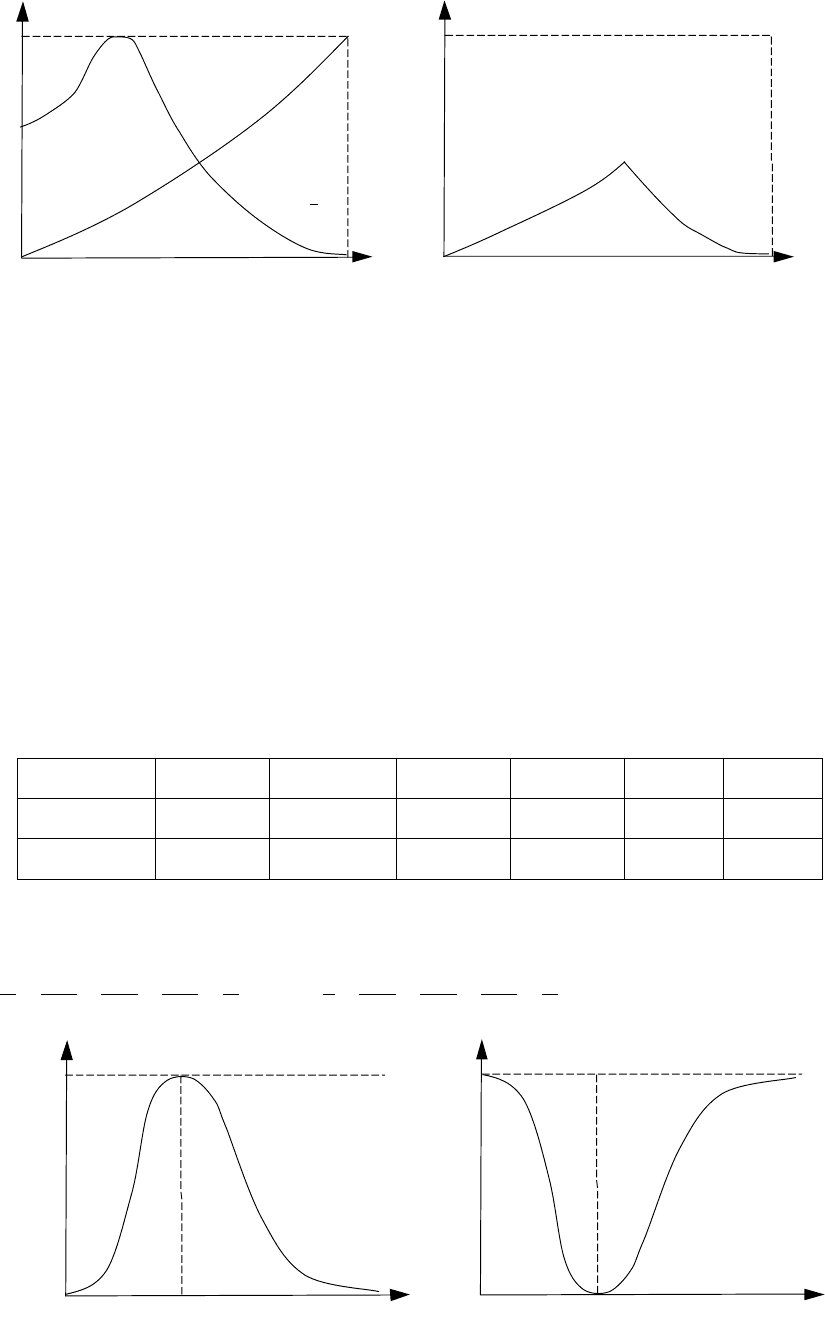
277
Рисунок 12.5 – Операция пересечения нечетких подмножеств:
а – исходные функции степеней принадлежности;
б – результирующая функция степени принадлежности
На рисунке 12.5 представлена графическая реализация операции пересечения
нечетких подмножеств Р и Q универсального множества U.
Дополнение нечеткого подмножества А универсального множества U
определяется выражением )u(1A
A
. Оно характеризует операцию
нахождения разности между единицей и значением функции принадлежности
A
для любого элемента и
U .
В таблице 12.8 представлена реализация операции нахождения дополнения
нечеткого подмножества A универсального множества U.
Таблица 12.8 – Операция нахождения дополнения нечеткого подмножества
U
1
2 3 4 5 6
A
(u)
0 0.1 0.3 0.5 0.8 1
B
(u)
1 0.9 0.7 0.5 0.2 0
Эту операцию можно представить в виде следующих записей:
5
1
4
8.0
3
5.0
2
3.0
1
0
A ,
5
0
4
2.0
3
5.0
2
7.0
1
1
A .
Рисунок 12.6 – Операция нахождения дополнения нечеткого подмножества:
а – исходная функция степени принадлежности;
б – результирующая функция степени принадлежности
а
б
P
U
C
0
0
1
1
u
u
Q
1Q
C
0
0
а
б
1
1
u
u
278
На рисунке 12.6 представлена графическая реализация операции нахождения
дополнения нечеткого подмножества Q универсального множества U.
Рассмотрим декартово произведение нечетких подмножеств. Пусть заданы
нечеткие подмножества А
1
и А
2
универсальных множеств U
1
и U
2
соответственно.
Декартово произведение нечетких подмножеств А
1
и А
2
обозначается A
1
.
А
2
и
понимается как нечеткое подмножество множества U, которое определяется
декартовым произведением (рисунок 12.7)
1
0.1
0.1 0.1 0.1
2
0.7
0.2 0.6 0.7
3
1
0.2 0.6 1.0
U
1
4
0.8
0.2 0.6 0.8
0.2 0.6 1.0
1 2 3
U
2
Рисунок 12.7 – Декартово произведение нечетких подмножеств: и
U
1
, и
U
2
Функция степени принадлежности декартова произведения A
1
.
A
2
определяется
выражением ))u(),u(min()u,u(
2A1A21AA
2121
Множество U+U
1
.
U
2
представляет собой совокупность всех пар (u
i
, и
j
), где u
i
U
1
,
u
j
U
2
.
На рисyнке 12.7 представлено декартово произведение нечетких подмножеств:
4
8.0
3
0.1
2
7.0
1
1.0
A
1
; .
3
1
2
6.0
1
2.0
A
2
Результат вычислений можно записать в следующем виде:
).3.4(8.0)2.4(6.0)1.4(2.0)3.3(0.1)2.3(6.0
)1.3(2.0)3.2(7.0)2.2(6.0)1.2(2.0)3.1(1.0)2.1(1.0)1.1(1.0AA
21
В этом примере были использованы два универсальных множества:
U
1
= {1, 2, 3, 4}, U
= {1, 2, 3}.
Нечеткое подмножество А универсального множества U.
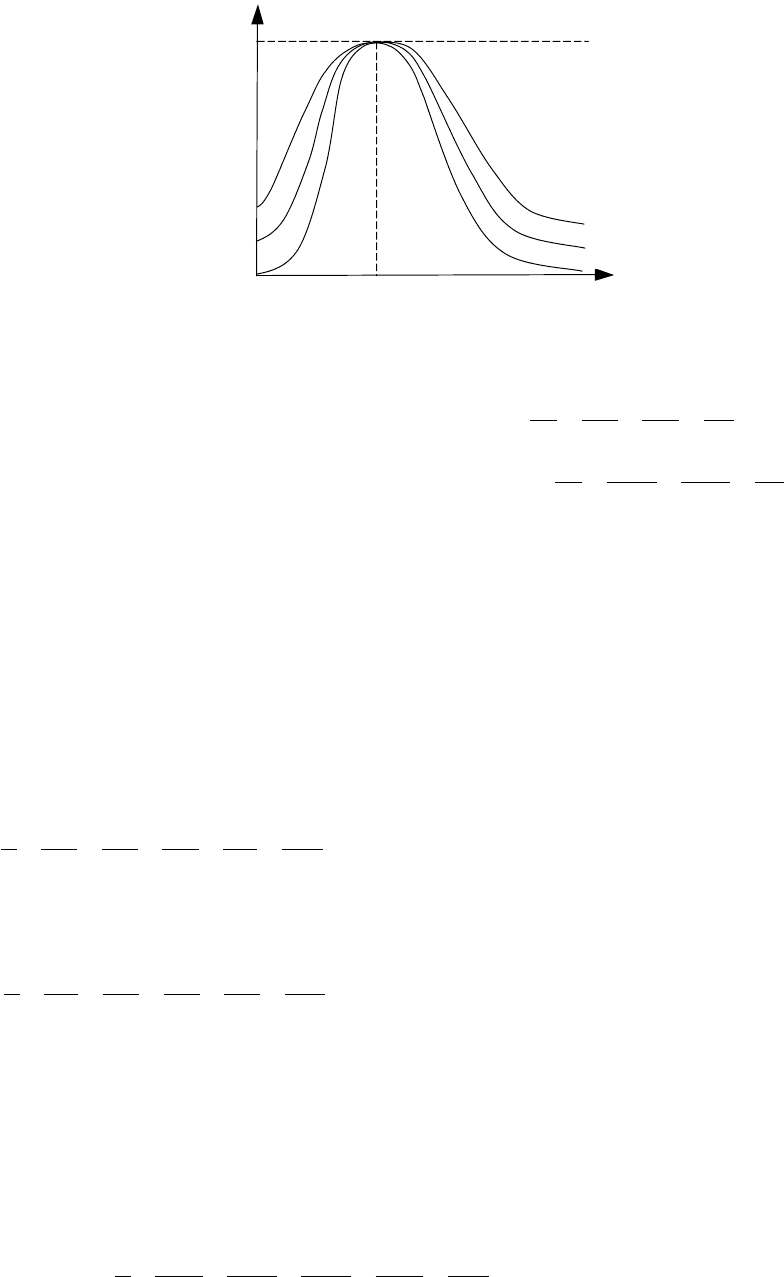
В случае а=2 эту операцию называют концентрированием и обозначают
А=соn(А).
279
0
1
u
dil
(A)
(A)
con
(A
)
u
i
Рисунок 12.8 – Операция концентрирования нечеткого подмножества
Пусть, например, имеется нечеткое множество
40
1
30
7.0
20
2.0
10
0
A . Применяя к
нему операцию концентрирования, получим
40
1
30
49.0
20
04.0
10
0
)A(con .
На рисунке 12.8 показан результат операции концентрирования.
12.3.5.3 Составные нечеткие термины
С помощью нечетких множеств можно осуществлять формализацию образования
составных терминов, которые характеризуют качественную информацию.
Рассмотрим эту операцию на конкретном примере.
Пусть заданы значения температуры, образующие универсальное множество
100806040200U
.
Термин «низкая» (температура) определим с помощью нечеткого множества
100
0
80
1.0
60
2.0
40
6.0
20
9.0
0
1
A
1
.
Термин «высокая» (температура) определим с помощью нечеткого множества
100
1
80
9.0
60
8.0
40
5.0
20
1.0
0
0
A
2
.
Наблюдения за технологическим процессом показали, что температуру в
некоторый момент времени можно характеризовать словами: «не очень низкая и
не очень высокая». Требуется построить нечеткое подмножество В, описываемое
составным термином «не очень низкая и не очень высокая», используя
необходимые операции над подмножествами А
1
и A
2
. Применяя операцию
концентрирования к подмножеству A
1
, получим:
100
0
80
01.0
60
04.0
40
36.0
20
81.0
0
1
A)A(con
2
11
.
Это подмножество соответствует термину «очень низкая». Теперь, применив
операцию концентрирования к подмножеству А
2
, получается подмножество,
соответствующее термину «очень высокая»:

280
100
1
80
81.0
60
64.0
40
25.0
20
01.0
0
0
A)A(con
2
22
.
С помощью операции дополнения получают подмножества
2
1
A
и
2
2
A
,
соответствующие терминам «не очень низкая», «не очень высокая». Наконец,
применив операцию пересечения, получают нечеткое подмножество,
характеризуемое составным термином «не очень низкая и не очень высокая»
(температура):
100
0
80
19.0
60
36.0
40
64.0
20
19.0
0
0
100
0
80
19.0
60
36.0
40
75.0
20
99.0
0
1
100
1
80
99.0
60
96.0
40
64.0
20
19.0
0
0
AAB
2
2
2
1
Результаты произведенных вычислений удобно представить в виде таблицы 12.9.
Анализ таблицы показывает, что наибольшая степень принадлежности нечеткому
подмножеству В наблюдается при 40 и 60°С, которые лежат в середине рас-
сматриваемого диапазона температур. Этот результат полностью соответствует
физическому смыслу решаемой задачи.
Таблица 12.9 – Формализация нечеткого подмножества для составного термина
«не очень низкая и не очень высокая температура»
Термин Температура, °С
0 20 40 60 80 100
«Низкая»
1 0.9 0.6 0.2 0.1 0
«Высокая»
0 0.1 0.5 0.8 0.9 1
«Очень низкая»
1 0.81 0.36
0.04
0.01
0
«Очень высокая»
0 0.01 0.25
0.64
0.81
1
«Не очень низкая»
0 0.19 0.64
0.96
0.99
1
«Не очень высокая»
1 0.99 0.75
0.36
0.19
0
«Не очень низкая и не очень высокая»
0 0.19 0.64
0.36
0.19
0
12.3.5.4 Способы задания функций принадлежности
Одним из центральных вопросов при формализации качественной информации
является задание функций степеней принадлежности в нечетких подмножествах,
которые отражают различного вида неопределенности, задаваемые словесно. При
нахождении функций степеней принадлежности весьма важно, чтобы такая
формализация терминов не зависела от семантики конкретных фактов и событий.
Важность этапа формализации качественной информации определяется тем, что
от корректности его выполнения в конечном итоге зависит степень достоверности
результата решения задачи с использованием качественной информации.
