Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis

Подождите немного. Документ загружается.

13.4 Reaction coefﬁcients in gradual transformations for p = c 285

transform to α + γ when the system crosses the four-phase plane. However, since the

extra amount of β is present in the β + δ mixture over the whole specimen, there are no

particular β regions predestined not to take part in the β + δ → α + γ transformation.

The progress of the transformation will determine which parts of β will not transform

and, afterwards, they will be found scattered all over the specimen. The α, present before

the four-phase reaction, may indirectly take part in the reaction by providing favourable

sites for the precipitation of α.

Exercise 13.5

Suppose the δ phase in Fig. 13.3(b) is a liquid and that the average composition of the

system is such that the liquid will be just about consumed by the four-phase reaction.

What phases will the system contain at a temperature just below the four-phase plane.

Hint

Suppose there is full equilibrium at each temperature. Remember that the amount of a

phase in a three-phase assemblage is given by the position in the three-phase triangle.

Solution

At an earlier stage the composition may fall inside the α + β + δ(L) or β + γ + δ(L)

triangle. If a very slight amount of liquid should remain below the four-phase temperature

then the system would be in the α + β + δ(L) triangle. If the liquid would be just about

consumed then the system, should fall on the α + γ line.

13.4 Reaction coefﬁcients in gradual transformations for p = c

Let us now consider a gradual transformation in a closed system with p = c by keeping

pressure constant and changing the temperature. In order to write a reaction formula with

the mass balance conserved it is now necessary also to include the change in composition

of regions not taking part directly in the phase transformation. As a simple example of

p = c = 2, consider the precipitation of Al

Cu from α phase, a solution of Cu in fcc-Al.

The solubility decreases with decreasing temperature at constant pressure and there will

thus be a gradual precipitation of Al

Cu. One way of writing this reaction would be

α(transformed) + Cu(from remaining α) → Al

Cu. (13.15)

The reaction coefﬁcients can then be evaluated with the same method used for sharp

transformations with p = c + 1but with the extra supply of Cu introduced instead of

the missing phase c + 1. However, it should be emphasized that this way of writing the

transformation is not unique. Another possibility would be

α(to be transformed) → Al

Cu + Al(to the remaining α). (13.16)

286 Transformations in closed systems

(AC)

(BC)

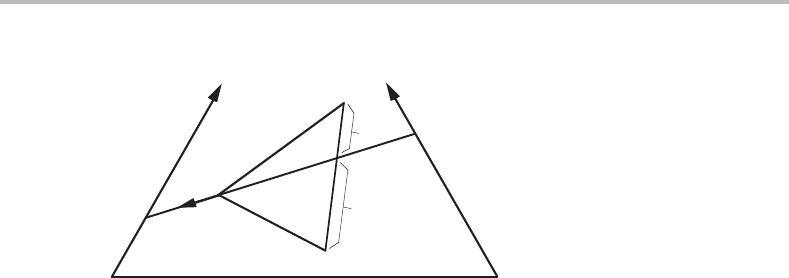
Figure 13.4 Gradual three-phase transformation in a ternary system. The arrow shows the

direction of change in composition of the L phase.

In order to deﬁne a unique way one would have to specify some special criterion. If one

is interested in the mechanism of the transformation, then one should consider exchange

of both Cu and Al but in proportions balanced according to their rates of diffusion in the

α phase.

A three-phase transformation in a ternary system is another case of gradual transfor-

mation, now with p = c = 3. An example was given in Fig. 12.22 but inFig. 13.4 it

is reproduced with the composition triangle included. Two of the ways of writing this

transformation are

L + (BC) → α + β (13.17)

L → α + β + (AC), (13.18)

where (BC) and (AC) represent the compositions one can read on the two sides of the

composition triangle. In each case one can calculate the reaction coefﬁcients by including

(BC) or (AC) instead of the missing phase c + 1. The ratio between α and β will indeed

be independent of whether one includes (BC) or (AC). It will be b/a according to the

lever rule.

Exercise 13.6

In an Al–Cu–Si specimen at 1 bar and 803 K one ﬁnds that the phases have the follow-

ing compositions at equilibrium: α(0.025Cu; 0.006Si) +L(0.16Cu; 0.05Si) + Al

Cu.

When the temperature is decreased, L changes in the direction away from the point

0.83Al;0.17Cu. Calculate the relative amounts of α and Al

Cu in the eutectic structure

formed by L → α + Al

Cu on further cooling. (The numbers given above are molar

contents.)

Hint

We have c = 3 and p = 3but we should write the transformation in a way resembling

a sharp transformation for p = c + 1. The relative amounts of the two phases are then

obtained as the ratio of their reaction coefﬁcients.

13.5 Driving force for sharp phase transformations 287

Solution

Write the reaction as L + (0.83Al; 0.17Cu) → α + Al

Cu. Eq. (13.11) yields

= (−1)

3−1

Al Cu Si



−0.79 −0.16 −0.05

−0.83 −0.17 0

210



=+0.0245

= (−1)

4−1

Al Cu Si



−0.79 −0.16 −0.05

−0.83 −0.17 0

0.969 0.025 0.006



=+0.00719

/ν

= 0.00719/0.0245 = 0.2935 = 0.23:0.77.

13.5 Driving force for sharp phase transformations

The driving force for the precipitation of a new phase under a gradual transformation in

a closed system was discussed in Section 7.7.Asanintroduction to a discussion of the

driving force for a sharp transformation we shall now consider a eutectoid transformation

in a binary alloy. We have seen that it usually gives rise to an intimate mixture of the two

new phases, illustrated by Fig. 12.5.Itmay give the material advantageous properties.

The most famous example is pearlite, the eutectoid formed from the austenite phase in

steel.

Because the rate of transformation is controlled by slow diffusion and evolution of the

heat of transformation will thus be slow, it is often possible to control the temperature and

it makes sense to discuss the transformation under isothermal conditions, for instance

at T

in Fig. 12.6. The character of the transformation as sharp is evident from its

progress. A region has either been completely transformed or is not at all affected. The

transformation occurs by the growth of colonies composed of an intimate mixture of the

two new phases and, under isothermal conditions, the growth continues until the whole

system has transformed.

It is well knownthat the mixture will be the ﬁner, the lower the temperature of formation

is. The reason is that the interfaces in the mixture have surface energy and cannot

form without the supply of a corresponding amount of driving force. According to an

approximate treatment, one-half of the available driving force goes into surface energy

and the other half is used for driving the diffusion.

The conditions for cooperative growth of the two new phases can be illustrated by

extrapolating the phase boundaries in the T, x

phase diagram as shown in Fig. 12.6. This

kind of construction is given again in Fig.13.5(a) but a solid phase, γ, has been substituted

for the liquid phase and the diagram has been rotated. The transformation temperature is

now denoted by T

. The diagram shows how one can evaluate the composition difference

driving the diffusion in each one of the phases if there is local equilibrium with the γ

phase (see the arrows in Fig. 12.5).

288 Transformations in closed systems

αβ

∆x

∆ µ

∆x

(a) (b)

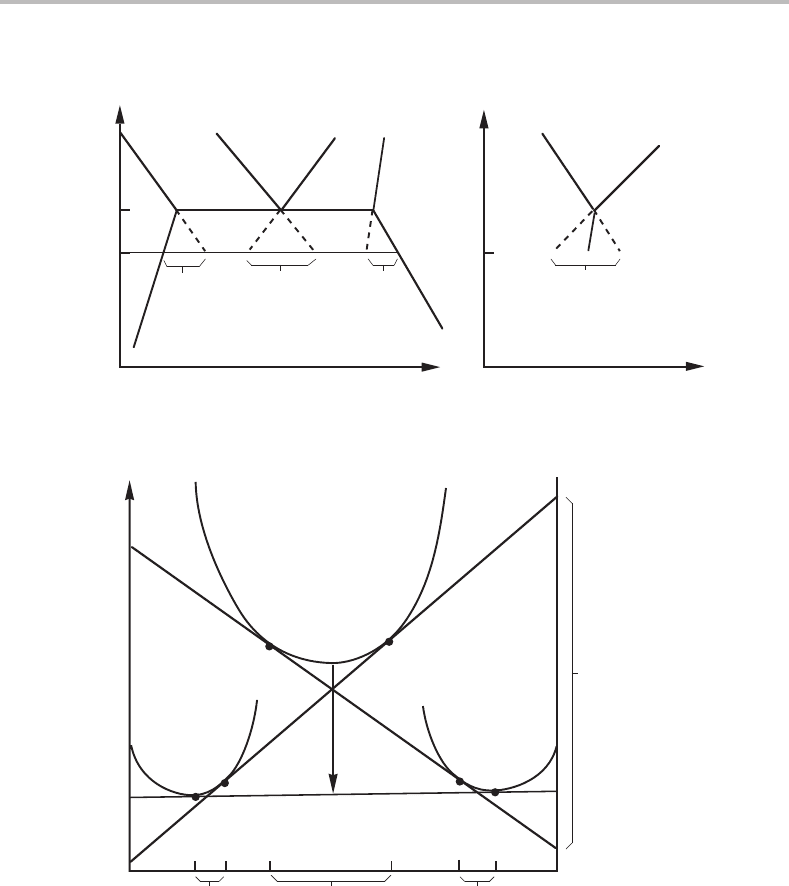
Figure 13.5 Evaluation of the differences in composition (a) and chemical potential (b) driving

the diffusion in a three-phase transformation in a binary system.

−∆G

∆x

∆µ

Figure 13.6 Gibbs energy diagram illustrating the eutectoid transformation γ → α + β at T

Fig. 13.5.

A similar construction in the T,µ

phase diagram in Fig. 13.5(b) yields a difference in

chemical potential of B, µ

,which may be used in a treatment of the rate of diffusion

of B in γ, although the composition difference is usually used for that purpose. The

conditions for the eutectoid reaction γ → α + β may also be illustrated with a molar

Gibbs energy diagram at T

(see Fig. 13.6).

As explained in Section 7.7, the driving force for the precipitation of a new phase in

agradual transformation decreases during its growth but for the whole reaction one can

deﬁne and evaluate an integrated driving force along the reaction path. This problem is

13.5 Driving force for sharp phase transformations 289

absent if the phase transformation is a sharp one because the parent phase which has not

yet transformed has not changed at all. Under constant T and P the driving force is thus

constant and the integrated driving force is equal to the momentary driving force if they

are both expressed per mole of the transformed structure. Under constant T and P we

obtain, by identifying the extent of the transformation, ξ , with the number of moles of

the products which is also equal to the number of moles of transformed reactants,

D =−



∂G

∂ξ



T,P,N

=−G

(products) + G

(reactants). (13.19)

This quantity is illustrated in Fig. 13.6 for a eutectoid transformation γ → α + β in a

binary system.

The value of the driving force may be calculated using the reaction coefﬁcients for a

sharp phase transformation at ﬁxed composition. Per mole of the reactant, γ,weobtain

from Eq. (13.12),

D =−G

=−



/(−ν

) =−







. (13.20)

Even though this expression looks quite simple, it may sometimes be difﬁcult to evaluate

all the molar contents to be inserted. A useful approximation would be to assume that

all the phases have the same compositions they have at the equilibrium temperature. If

it is further assumed that the resulting value of G

varies linearly with temperature,

we could use the method introduced in Section 3.9 for a transformation that we now

recognize as a sharp one. Since D stays constant for a sharp transformation, we get

S(T

− T

) = H(T

− T

)/T

=−G =



Ddξ = D



dξ = Dξ. (13.21)

Let ξ be the number of moles transformed. The driving force for the transformation

of one mole is thus

D = S

− T

) = H

− T

)/T

. (13.22)

Here, T

is the equilibrium temperature and T

is the actual temperature of the transfor-

mation. For small T the heat of transformation may be taken as the value at T

.Itmaybe

available from direct measurements. For larger undercoolings one may have to consider

variations of H

with temperature, for instance due to changes of the compositions of

various phases.

Let us now examine the situation below the equilibrium temperature in more detail.

Figure 13.6 demonstrates the complexity found in a eutectoid transformation in a binary

system. Each one of the phases is in contact with the other two phases and two dif-

ferent compositions are thus deﬁned for each phase. Figure 13.5 shows how they are

obtained from the phase diagram by extrapolating the phase boundaries to the tempera-

ture of transformation T

under the assumption of local equilibrium at all the two-phase

interfaces.

The situation gets even more complicated if one tries to analyze how the driving force

is consumed during the transformation. This is illustrated in Fig. 13.7. This diagram

demonstrates several complications. Firstly, α and β grow under an increased pressure

290 Transformations in closed systems

α(P)

β(P)

−∆G

∆x

∆µ

Figure 13.7 Molar Gibbs energy diagram for a binary system with a eutectoid transformation,

showing three dissipations of the driving force, G

, G

and G

because the interfaces to the parent γ are curved (as illustrated in Fig. 12.5). The corre-

sponding −G

is consumed by the creation of all the α/β interfaces in the eutectoid

structure. Secondly, the two new phases are not formed with their ﬁnal compositions,

which are governed by the α/β equilibrium, because they grow from the γ phase. The

corresponding −G

is consumed by diffusion from the interior of α to the interior of β

behind the reaction front. The remaining part of the driving force, −G

,isconsumed

by diffusion at the reaction front.

As already mentioned, according to an approximate treatment of the rate of transfor-

mation, the highest growth rate is obtained when one-half of the total driving force goes

into the surface energy of all the α/β interfaces.

Exercise 13.7

The difference in chemical potential of B driving the diffusion in the γ phase during

the eutectoid transformation, shown in Fig. 12.5,was identiﬁed in Fig. 13.5(b).Find the

corresponding differences for α and for β.How are the three related?

Solution

µ

is found between the lines for γ/α and β/α and µ

is found between the lines

for β/α and β/γ. Evidently, µ

= µ

+ µ

13.6 Driving force under constant chemical potential 291

Exercise 13.8

The heat of formation of pearlite from austenite is H

=−4.5 kJ/mol and the equi-

librium temperature is T

= 1000 K. Estimate the coarseness of pearlite formed at

= 950 K, assuming that all the driving force goes into interfacial energy between the

two phases of pearlite. Suppose that the interfacial energy is approximately σ = 1 J/m

and the molar volumes of all the phases are approximately V

= 7 × 10

−6

/mol.

Compare with an experimental value of the coarseness, w = 0.14 µm.

Hint

w is the total thickness of one lamella of each phase in pearlite. One mole of pearlite

then contains an area of 2V

/w of interfaces.

Solution

The total interfacial energy is 2σ V

/w J/mol. The driving force is (H

)(T

−

). Thus, 2σ V

/w = (H

)(T

− T

); w = 2σ V

/(−H

)(T

− T ) = 2 ×

1 × 7 × 10

−6

× 1000/4500 ×50 = 6 × 10

−8

m = 0.06 µm.

The observed value is about twice as large, which is expected if only one-half of the

driving force should go into interfacial energy.

13.6 Driving force under constant chemical potential

In the preceding section it was shown how the driving force for a sharp transformation

can be estimated from the undercooling T at which the transformation occurs. In the

same way, the driving force for a γ-eutectoid transformation in a ternary A–B–C system,

controlled by the chemical potential of a mobile component C under constant T and P,

should depend upon the difference in chemical potential of C during the transforma-

tion and at equilibrium, µ

.Wecan illustrate the conditions by extrapolations in the

, u

phase diagram in Fig. 12.24 or in the corresponding µ

,µ

phase diagram (see

Fig. 13.8 where the diagram has been rotated in order to emphasize the similarity with

the binary case in Fig. 13.5).

Since µ

is assumed to be constant instead of N

,wemust evaluate the driving force

from a new alternative of the combined ﬁrst and second law,

Ddξ = V dP − SdT +



j=C

+ µ

− dG + N

dµ

− N

dµ

= V dP − SdT +



j=C

− N

dµ

− d(G − N

) (13.23)

where G − N

is a new characteristic state function. At constant T, P, N

and µ

we get

Ddξ =−d(G − N

). (13.24)

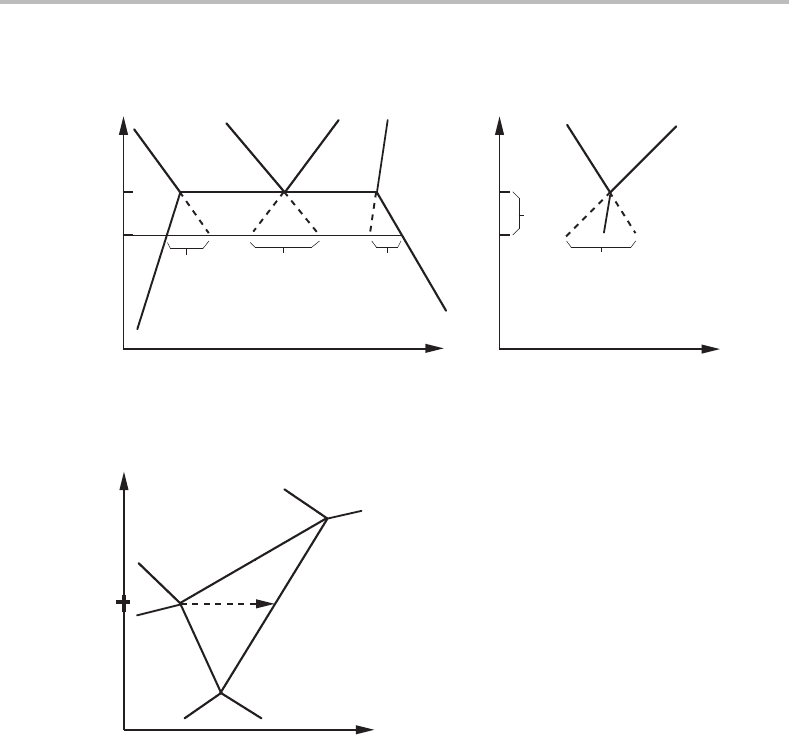
292 Transformations in closed systems

∆ µ

(a) (b)

∆x

∆ µ

∆x

Figure 13.8 Evaluation of the driving force,µ

, for an isobarothermal transformation under

changing C content in a ternary system.

∆u

Figure 13.9 Sharp transformation γ → α + β in a ternary system with a mobile component, C.

The increase of the C content can be read directly.

However, by identifying the extent of the transformation, ξ , with the increased content

of C, N

,wereturn to more well known quantities,

D =−(∂ G/∂ N

)

T,P,N

+ µ

=−

+ µ

= µ

. (13.25)

By deﬁnition, the ﬁrst term is the chemical potential of C at equilibrium. Therefore,

D = µ

−

= µ

. (13.26)

This is the driving force per mole of C added to the system. It should be multiplied by

the amount of C required by the transformation. That quantity is conveniently expressed

in terms of the u

fraction, the amount of C per mole of A + B. Figure 13.9 demon-

strates how the increase u

can be evaluated graphically and the driving force for the

transformation γ → α + β expressed per mole of A + Bisgivenby

D = u

× µ

13.6 Driving force under constant chemical potential 293

0.02

0.2 0.4

0.10

cementite

Figure 13.10 See Exercise 13.9.

Figure 13.9 resembles Fig. 12.24 but the choice of u axis makes the arrow horizontal.

The analytical evaluation of u

is described in the next section.

Exercise 13.9

In the Fe–C system the γ phase exists above 1000 K and at lower temperatures it trans-

forms to a lamellar aggregate of α and cementite (Fe

C) that is called pearlite. The phase

diagram (Fig. 13.10) for 923 K shows that it is possible to stabilize γ by the addition

of Mn. Consider an alloy composed of γ with a composition falling exactly on the γ

corner of the α + γ + cementite triangle at 923 K. That alloy must have a C activity of

0.7. By carburizing such an alloy one can form a surface layer of pearlite. Estimate its

coarseness if one carburizes with an atmosphere having a carbon activity of 0.9. Use the

values V

= 7 × 10

−6

/mol and surface energy σ = 1J/m

Hint

It should ﬁrst be realized that we do not know how much of the difference in carbon

activity is lost by driving the diffusion of carbon through the carburized layer. In order to

get a numerical result, let us assume that all the driving force acts at the reaction front.

The increase of the C content is obtained from a horizontal construction in the three-

phase triangle. The increase in C potential is obtained from the activity through µ

+ RT ln a

. Assume that half of the driving force goes into surface energy. Express

the coarseness with w, the total width of one lamella of α and one of cementite. The area

of α/cementite interfaces is then 2V

/w per mole of the material and we thus get the

relation 2V

σ/w = 0.5 ×u

µ

Solution

By measuring the horizontal distance of the γ point from the α + cementite side

of the triangle we get µ

= 0.08. By comparing the C activities we get µ

294 Transformations in closed systems

RT ln(0.9/0.7) = 1930 J/mol and using half of this we ﬁnd w = 2V

σ/0.5u

µ

2 × 7 × 10

−6

× 1/0.5 ×0.08 × 1930 = 2 × 10

−7

m = 0.2 µm.

13.7 Reaction coefﬁcients at constant chemical potential

In Section 13.2 we were able to calculate the fractions of the various phases taking

part in a sharp transformation in a system of constant composition because p was equal

to c + 1. Now we shall consider the case p = c where one of the components is very

mobile and is controlled through its potential. The total contents of all the other com-

ponents in the system will be kept constant, i.e. n

= c − 2. Together with the constant

potential and pressure we have n

= c − 2 + 1 +1 = c and instead of Eq. (13.3)we

now obtain d = c + 2 − p − n

+ n

= c + 2 − c − c + (c − 2) = 0. This will also be

a sharp transformation. The mobile component will be denoted C and will be given the

number c.Bynot considering that component we get the same condition as before but

must now express the molar contents without regard for the mobile component. Thus

we must use the u variable instead of the ordinary molar content x, and we obtain for

instance



..u

c−1



. (13.27)

The mobile component is not included in the determinant. The amount of the γ phase

taking part in the reaction, ν

,ishere expressed without regard for the mobile component.

The change in content of the mobile component can be evaluated just like the change of

any other molar quantity using Eq. (13.12).

u



..u

c−1



. (13.28)

This is the increase of C per mole of units of the reaction formula as given by the ν

values. If γ is the only reactant and all the other phases are products, it is interesting

to evaluate u

per mole of all the other components in γ.Itisobtained by dividing

with – ν

u



..u

c−1







..u

c−1



. (13.29)

If a mixture of α and β in the ternary A–B–C system is treated under conditions of a

lower chemical potential for C, the system will move from right to left in Fig. 13.9 and

one should expect the reverse transformation

α + β → γ + C(sink).

This is a peritectoid transformation and one should primarily expect the new γ to form

at the α/β interfaces. If the transformation is not inhibited due to slow diffusion of the

two sluggish elements, it will look almost as a sharp phase transformation.

Exercise 13.10

The equation for u

, the addition of a mobile component C consumed by a sharp

transformation, can be applied to the reaction γ + C(source) → α + β in a ternary

system at constant T and P and the result will be u

/ν

=|u

|/|u

|. Show