Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis

Подождите немного. Документ загружается.

14.6 Transformations in steel under quasi-paraequilibrium 315

quasi-paraequilibrium

paraequilibrium

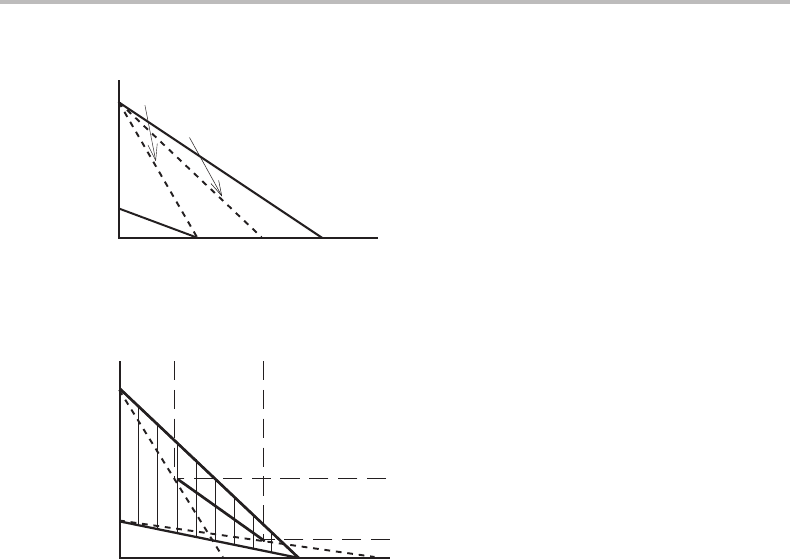
Figure 14.13 Comparison of two partitionless growth conditions for the γ → α transformation in

a ternary system with a very mobile component C.

Figure 14.14 Solution to Exercise 14.5.

Hint

Find tie-lines in Fig. 14.11(c) by projection from Fig. 14.11(a) and (d).

Solution

The α + γ two-phase ﬁeld under paraequilibrium is a line in Fig. 14.11(b) and there are

no tie-lines. A tie-line in Fig. 14.11(c) is shown in Fig. 14.14.

14.6 Transformations in steel under quasi-paraequilibrium

In a steel with carbon and some substitutional alloying elements it often happens that

anew phase forms with the same alloy content as the parent phase but with a different

carbon content. Such a phase transformation may occur under local paraequilibrium at

the migrating interface, or under quasi-paraequilibrium, or in between. In this section we

shall examine the quasi-paraequilibrium case, using results from the preceding section.

As a simple example we shall ﬁrst discuss the γ → α transformation. In a u

phase

diagram all products of a paratransformation or a quasi-paratransformation will fall on

the same horizontal line as the parent phase. In the phase diagram we can easily ﬁnd

a point representing the composition of a growing phase, because it must fall on the

correct level of alloy content but also on the appropriate phase boundary, the α/γ phase

316 Partitionless transformations

γα

alloy

(a) (b)

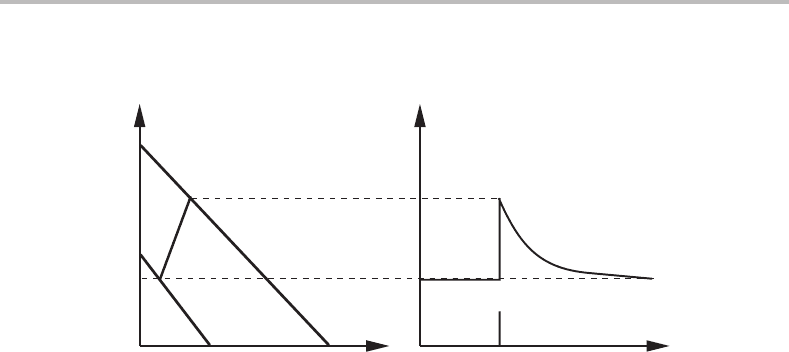
Figure 14.15 Construction yielding the conditions at the phase interface for a

quasi-paratransformation γ → α in a ternary system with a mobile component C.

boundary in the present case. Having located that intersection we have found a tie-line

representing the local equilibrium conditions at the migrating α/γ interface. We can

thus construct a composition proﬁle for the alloying element. In order to do this we shall

plot u

on the ordinate axis (see Fig. 14.15).

From the composition proﬁle we may conclude that there is a thin spike of the alloying

element in front of the migrating interface. This is similar to the quasi-diffusionless case

in a binary alloy. According to the mathematics of diffusion, we can estimate the width

of the spike to D

/υ,where υ is the rate of migration of the interface and D

the diffusion coefﬁcient of the alloying element M relative to Fe. The width is usually

extremely small and the alloy content in the spike originates from a transient stage of

growth at a very early time.

One may normally expect that the rate is governed by the rate of long-range diffusion

of carbon. In order for the transformation to proceed, carbon must diffuse from the α/γ

interface and into the interior of the γ phase because the growing α phase has less carbon

than γ.Itisthus necessary that the carbon potential is higher at the interface than in

the interior of the γ phase. The critical limit for the position of the initial γ phase is

thus found on the intersection of the level of alloy content, u

alloy

, and the isoactivity line

for carbon in γ which goes through the γ end-point of the tie-line. This construction

is shown in Fig. 14.16. Naturally, this isoactivity line must be extrapolated below the

γ/(α + γ) boundary. The critical limit is represented by a circle in the diagrams and falls

on the line for quasi-paraequilibrium in Fig. 14.13. The rapid, quasi-paratransformation

can only occur on the left-hand side of that critical line, i.e. in this case below the

line.

Suppose the carbon activity for a γ phase is initially lower than for the isoactivity

line in Fig. 14.16. The γ → α transformation can then start in the way described above.

However, during the growth of α, the γ phase will accumulate more and more carbon.

Its carbon activity will increase and eventually reach the value for the isoactivity line in

Fig. 14.16. The rapid growth will then stop and the transformation can only continue at

a much slower rate which permits the sluggish alloying element M to be redistributed

14.6 Transformations in steel under quasi-paraequilibrium 317

rapid

γ→α

alloy

isoactivity line

for C in γ

(a) (b)

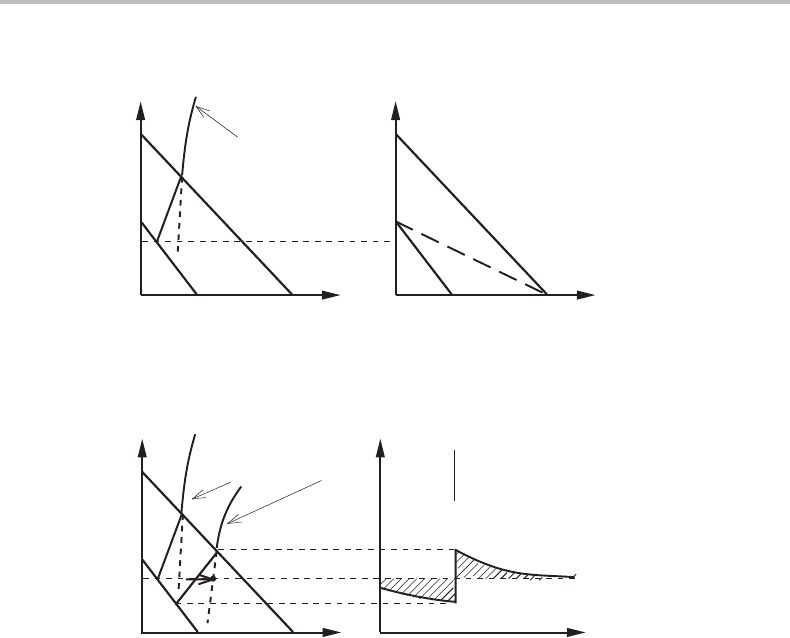
Figure 14.16 Construction yielding the critical limit for a quasi-paratransformation γ → α in a

ternary alloy with a mobile component C.

αγ

alloy

isoactivity

lines for C in γ

(a) (b)

Figure 14.17 Growth conditions of α from γ at a stage where diffusion of the sluggish alloying

element M is required.

relative to Fe. During this stage of slow growth there will be sufﬁcient time for the mobile

carbon to equilibrate inside the system and at each moment all the γ phase present may

fall practically on a common isoactivity line for carbon in γ.Ifweknow the momentary

composition of the interior of the γ phase we can easily ﬁnd the γ end-point of a tie-line

representing the equilibrium conditions on the migrating α/γ interface. We can thus

construct the composition proﬁle for the alloying element M during any stage of very

slow growth; see Fig. 14.17 in which the ﬁlled circle represents the present composition

of the interior of the γ phase and the arrow indicates that its carbon content is gradually

increasing during this growth. In the composition proﬁle the spike has now widened to

a considerable thickness, which may be evaluated by using the fact that the two shaded

areas represent the same amount of M. The rate of growth is now governed by diffusion

of the alloying element down the spike.

Let us now examine the more complicated case where the γ phase transforms to the

eutectoid mixture of α and cementite, (Fe,M)

C, which is called pearlite. In order for

that reaction to be governed by the rate of carbon diffusion it is necessary for both α and

cementite to inherit the alloy content of the parent γ. Each one of the two growing phases

must fall on the correct side of its critical line. We shall ﬁrst illustrate this by two separate

phase diagrams in Fig. 14.18(a) showing the α/γ equilibrium and (b) showing the

318 Partitionless transformations

rapid

γ→α

α+γ

rapid

γ→cementite

γ+cementite

(a)

(b)

Figure 14.18 The critical limit for the quasi-paratransformation of γ to (a) α; and (b) cementite in

an Fe–M–C alloy.

γ+cementite

α+γ+cementite

α+cementite

α+γ

cementite

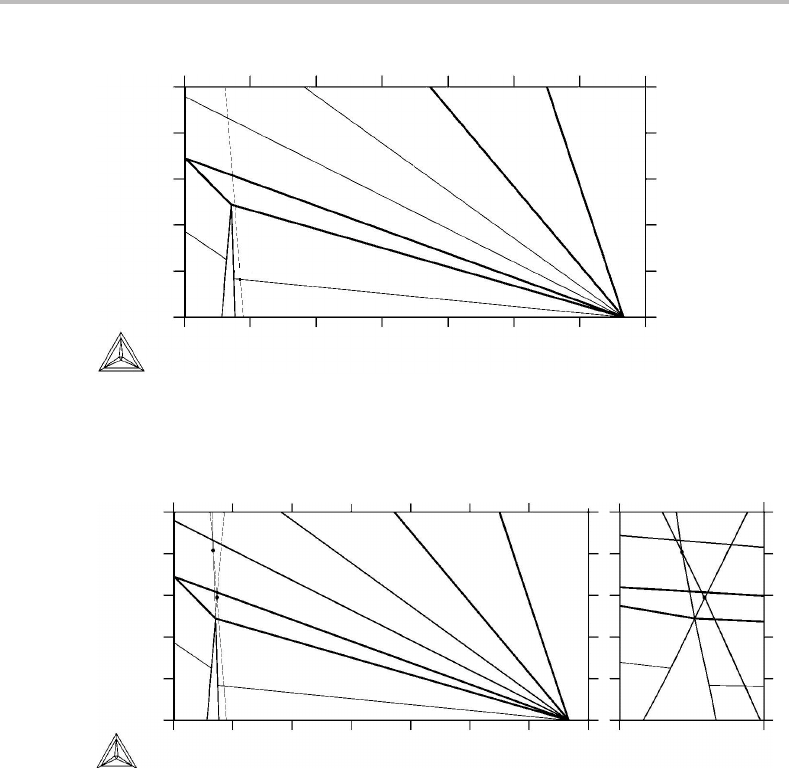
Figure 14.19 Phase diagram for an Fe–M–C system, illustrating the conditions for a rapid

formation of α + cementite (so-called pearlite) under quasi-paraequilibrium (see shaded

triangle).

γ/cementite equilibrium. The position of the region for rapid precipitation of cementite,

relative to the full equilibrium phase boundary, has been drawn in agreement with the

general rule that the paraequilibrium phase boundaries lie inside the full equilibrium

two-phase ﬁeld.

If the alloy is at a temperature where the γ → α + cementite transformation is pos-

sible, the two two-phase regions α + γ and γ + cementite must overlap to some degree

and there must be a three-phase α + γ + cementite region, as illustrated in Fig. 14.19.

This phase diagram resembles the Fe–Ni–C phase diagram because Ni prefers to

dissolve in γ rather than in α or cementite. The metastable parts of the phase boundaries

have been drawn with dotted lines. The two critical lines form a small triangular region

which we may regard as a critical triangle. Rapidly growing quasi-parapearlite can be

expected to form from a γ phase situated inside the critical triangle. A γ phase situated

to the left of the triangle should ﬁrst precipitate so-called proeutectoid α and thus move

into the triangle where pearlite can start forming. A γ phase situated to the right of

the triangle should ﬁrst precipitate proeutectoid cementite and then pearlite. However, a

requirement is that the level of alloy content falls below the top of the triangle. Otherwise,

14.7 Transformations in steel under partitioning of alloying elements 319

the rapid, proeutectoid precipitation will stop at its critical line. The transformation can

continue only by the slow rate of diffusion of the alloying element into the interior of the

austenite because both α and cementite must dispose of nickel into the parent γ. That

should normally be a very slow reaction and pearlite formed under such conditions has

not been reported. In solidiﬁcation, the growth conditions for a eutectic may be similar

but the rate of diffusion in the liquid phase is so rapid that the eutectic reaction is not

inhibited above the triangle for the rapid eutectic transformation.

Exercise 14.6

An Fe–Ni alloy with u

= 0.01 is ﬁrst in the state of γ (fcc) at 1273 K but then it

is carburized and cementite (Fe

C) forms isothermally. Suppose one would like to try

to produce homogeneous cementite with u

= 0.01. Estimate what carbon activity is

required during the carburization. It is known that the γ + cementite equilibrium in the

binary Fe–C system is 1.01 at 1273 K. It is also known that the distribution coefﬁcient

for Ni between cementite and γ is K

cementite/γ

= 0.26.

Hint

Inspiration can be obtained from Fig. 14.18(b) because formation of cementite with the

initial Ni content can only occur under a rapid reaction. However, in order to calculate

the necessary carbon activity we can go to Section 11.3. The carbon content of cementite

is u

= 1/3 and for γ it is about 0.073.

Solution

If the growing cementite has u

= 0.01 and there is local equilibrium (quasi-

paraconditions) then the adjoining γ has u

= 0.01/0.26 = 0.038. Equation (11.23)

gives ln(a

binary

) =(1 −0.26)/[(1/3) −0.073] ×0.038 =0.108; a

=1.01 ×1.114 =

1.125. The carbon activity must be higher than this value.

14.7 Transformations in steel under partitioning of alloying elements

In the preceding section we concluded for Fe–Ni–C that, for Ni contents falling above the

top of the critical triangle, pearlite could grow only by nickel diffusing into the remaining

γ because both growing phases, α and cementite, require that the nickel content is lower

than in the adjoining γ. The situation will be quite different if one of the phases, α or

cementite, can grow with a higher alloy content than the adjoining γ. Then it would be

sufﬁcient that the alloying element diffuses side-wise and distributes itself between the

two growing phases. This process can take place with an observable speed by diffusion

inside the pearlite/γ interface. Interfacial diffusion can be orders of magnitude faster

than volume diffusion.

320 Partitionless transformations

0.05

0.04

0.03

0.02

0.01

0.05 0.10 0.15 0.20 0.25 0.30 0.35

α + γ

α+cementite

γ+cementite

Figure 14.20 See Exercise 14.7.

0.05

0.04

0.03

0.02

0.01

0 0.05 0.10 0.15 0.20 0.25 0.30 0.025 0.045

γ+cementite

α+cementite

α+γ

(a) (b)

Figure 14.21 Solution to Exercise 14.7.

Examples of alloying elements allowing pearlite to grow under partitioning between

α and cementite are manganese and silicon. Cementite will attract manganese and α will

attract silicon.

Exercise 14.7

Suppose a steel is ﬁrst transformed to homogeneous γ at a high temperature and then

cooled to 1023 K where it is represented by the cross in the Fe–Si–C phase diagram

(Fig. 14.20). The thin line is an isoactivity line for γ going through the cross. Examine if

there would be a positive difference in Si content inside γ, u

,todrive the redistribution

of Si between α and cementite and thus allow γ to transform to pearlite. If that is the

case, evaluate the fractions of α and cementite in that pearlite.

14.7 Transformations in steel under partitioning of alloying elements 321

Hint

First ﬁnd the intersections with the isoactivity line and the extrapolated phase boundaries

for γ. Then try to ﬁnd the other end-points on the corresponding tie-lines.

Solution

The construction is shown in Fig. 14.21(a) and again, with an expanded u

scale, in

(b). The intersection of the isoactivity line with the two phase boundaries will give the

compositions of γ at the interfaces to α and cementite if there is full local equilibrium.

The difference u

= u

γ/cementite

− u

γ/α

is positive and will thus make silicon diffuse

away from cementite to α.Pearlite can thus grow but it must have the same average

Si content as the initial γ, u

= 0.01. Since cementite has practically no Si and α has

about 0.035, we ﬁnd that the fraction of α is 0.01/0.035 = 0.3. The fraction of cementite

is thus 0.7 and the carbon content of this pearlite is extremely high. It requires a large

supply of carbon to be drawn from the interior of the γ phase.

Limit of stability and critical

phenomena

15.1 Transformations and transitions

In Chapter 12 we were mainly concerned with the question whether a transformation

is sharp or gradual. The difference between those cases is very practical and straight-

forward. It is based on a one-dimensional phase diagram where the only axis represents

the quantity that is being varied. If that diagram shows a two-phase ﬁeld of some exten-

sion between the two one-phase ﬁelds, then the transformation between the two phases

will be gradual. If the two-phase ﬁeld has no extension, then the transformation will be

sharp. For a unary system with a transformation this will happen if one varies a potential,

e.g. T. The Gibbs energy is a continuous function of T across the sharp transformation

but its derivatives, yielding S and V, show discontinuous jumps. This is why the phase

boundaries separate when a molar axis is introduced (see Figs 9.1 and 9.2). In other

cases there is no such separation because the ﬁrst-order derivatives are zero. A typical

example is found in a ferromagnetic substance, which gradually loses its magnetization

as the temperature is increased. At the Curie temperature it reaches zero and the sub-

stance has thus become paramagnetic. There is no temperature where ferromagnetic and

paramagnetic regions coexist in a pure substance, not even if one varies a molar quantity.

As a consequence, there is not really a two-phase ﬁeld between the two one-phase ﬁelds

and this fact is indicated by the use of a dashed line to separate the one-phase ﬁelds

(see Fig. 15.1 where the two phases are denoted by β and β



in order to emphasize their

close relationship). If there is no discontinuous jump in the ﬁrst-order derivatives but

there is one in the second-order derivatives, then one calls this a second-order transi-

tion as distinguished from a ﬁrst-order transition when there is a jump in the ﬁrst-order

derivatives.

When considering a T, P diagram and calculating the locus of a sharp transformation

between two phases in Section 8.3,weapplied the Gibbs–Duhem relation to each of

the phases, obtaining two equations for dµ

.Byrequiring that µ

must change in the

same way for the two phases along their line of coexistence, it was possible to calculate

the slope of that line, (see Fig. 8.6). In this way dP/dT was obtained as a function of

discontinuous jumps in the two ﬁrst-order derivatives, S and V . This method does

not work in the present case because the two equations become identical on the line we

want to calculate, and S and V both go to zero there. This problem was solved by

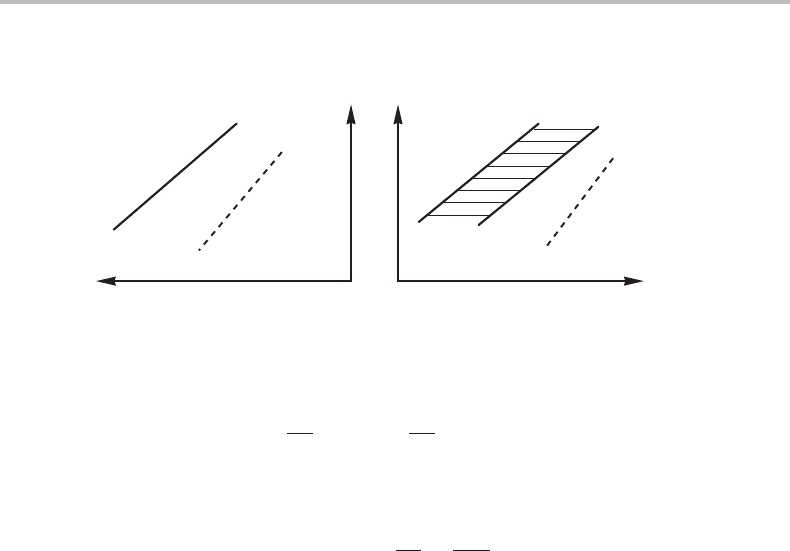
Ehrenfest [27]who instead used the fact that on the line there is no difference between

15.1 Transformations and transitions 323

β′β′

(a) (b)

Figure 15.1 Characteristics of a second-order transition β ↔ β



. The γ ↔ β transition is ﬁrst

order.

V of the two states. The expression for dV,

dV =



∂V

∂T



dT +



∂V

∂ P



dP = V α dT − V κ

dP, (15.1)

must give the same value in both states. Because V itself also has the same value in both

states but α and κ

do not, we get, by taking the difference between the two states,

α

κ

(15.2)

It is also possible that the discontinuous jumps ﬁrst occur in the third-order deriva-

tives of G and the corresponding transition would be of third order, etc. In practice, it

is often difﬁcult to decide by experimental measurements whether α and κ

differ

from zero, as they should for a second-order transition. Sometimes the individual values

of the second-order derivatives appear to go to inﬁnity at the transition point and it is

not meaningful to try to evaluate their difference. Ehrenfest’s expression for dP/dT is

then of little practical use. Of course, it can be used when one investigates a particular

model that gives deﬁnite values for second-order derivatives. In view of these complica-

tions, it is common to call all transitions with continuous ﬁrst-order derivatives, second

order.

It should be emphasized that nothing really happens in a system when it passes a

second-order transition point. It does not really transform. The only difference is that

it starts behaving in a new way. The real changes in the system occur gradually as the

system moves away from the point of transition. In that sense, the second-order transition

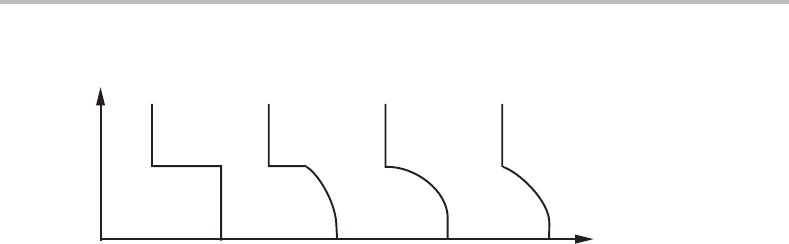
is just the start of a gradual transformation. Figure 15.2 illustrates different possibilities

for a pure substance at constant pressure. The internal variable ξ is some measure of the

arrangements of the atoms or electrons. Curve (a) with its discontinuous jump represents

a ﬁrst-order transition. Curve (b) shows a discontinuous jump but also a gradual change.

In curve (c) the jump has disappeared but the curve is horizontal at the break point. In

curve (d) the curve never turns horizontal.

The words transformation and transition are often used as synonyms. One word is

favoured by the experts in some ﬁelds and the other word in other ﬁelds. There is a need

for two words with different meanings. For our purposes, it would seem most natural

to use transition in much the same way as above but use transformation to describe the

324 Limit of stability and critical phenomena

(a) (b) (c) (d)

Figure 15.2 Different cases of transitions and transformations. (a) A ﬁrst-order transition that

occurs with a sharp transformation. (b) A ﬁrst-order transition where the transformation is

partly sharp, partly gradual. (c) and (d) Second-order transitions with completely gradual

transformations.

progress of the real changes occurring in a system. The break points in all the curves in

Fig. 15.2 would thus be regarded as the transition point and the transition is the change

occurring at the transition point, whether it is a real change or a change in behaviour

that will reveal itself as the system moves away from the transition point. In curve (a)

the ﬁrst-order transition yields a sharp transformation if T, being a potential, is varied.

In curve (b) part of the transformation would be sharp and occur at the transition point,

and another part would be gradual and occur below the transition point. In curves (c)

and (d) the transformation would be completely gradual and start as the transition point

is crossed. Thus, a transition point yielding a transformation that is at least partly sharp,

would be of ﬁrst order. Otherwise, it would be of second order. It should be emphasized,

however, that there are many cases where the concept of ﬁrst- and second-order transition

does not appear to be very useful. This will be demonstrated in Section 15.4.

The strict difference between ﬁrst-order and second-order transitions is of consider-

able theoretical interest but from a practical point of view it may sometimes be of less

importance whether there is a small discontinuous jump or no jump at all.

In the previous chapters, only the word transformation has been used. From now on,

an attempt will be made to apply both terms and with the deﬁnitions given here. In view

of the conclusion drawn in Section 12.2,asharp transformation, which must always be

a ﬁrst-order transition, will turn gradual when the variable is changed from a potential

to a molar quantity. From the theoretical point of view this is a trivial effect and should

not affect the classiﬁcation of the transition. The theoretical study of phase transitions is

thus carried out without involving any molar quantity.

A phase transition is often caused by a tendency of an ordered arrangement to disorder.

Such transitions are called order–disorder transitions and the driving force comes

primarily from the increasing conﬁgurational entropy. In other cases, the cause may

be the lowering of the energy by deformation of the structure, e.g. by decreasing the

tetragonality, without changing the conﬁgurational entropy. Such transitions are called

displacive transitions.Ofcourse, the characteristics of order–disorder and displacive

can be applied to the corresponding transformation, as well. In both cases, the progress

of the change can be expressed by some internal variable, e.g. the degree of long-range

order or the tetragonality. For simplicity, all such variables are sometimes called ‘order

parameters’ and, in principle, all internal variables could play this role.