Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis

Подождите немного. Документ загружается.

15.2 Order–disorder transitions 325

Another method of classifying phase transitions is based on what happens to the atoms

during the transition. A reconstructive transition involves a reorganization of the atomic

arrangement with the breaking of atomic bonds and the formation of new bonds. The

opposite case would be a displacive transition which involves only small adjustments of

the atomic positions without the atoms ever losing contact with their initial neighbours.

This classiﬁcation thus depends on the nature of the interface migrating through the parent

crystal. If the two crystal structures are closely related, one could imagine an interface

so highly coherent that the atoms ﬁnd their positions in the new crystal (phase) with only

small adjustments of their positions relative to each other. However, it is possible in the

same material that another interface is incoherent and one could not predict exactly where

an atom from the parent crystal will end up in the growing crystal. The transition would

then be regarded as reconstructive even if the structures of the two crystals (phases) are

identical. That is the case in ordinary grain growth where large crystals consume small

ones of the same phase and composition.

Furthermore, we may deﬁne a partitional transition as a transition in an alloy where

the new phase has a different composition and can grow only under long-range diffusion.

The solute atoms have partitioned between the parent phase and the new phase, which

requires diffusion and may be regarded as a diffusional transition. The opposite case is

a partitionless transition which would be the result if there is no diffusion. However, the

result could be partitionless even if there is some local diffusion during the transition. We

shall apply the term diffusionless only to cases where there is not even any short-range

diffusion. Evidently, a diffusional transition can at the same time be reconstructive or

displacive. It can even be an order–disorder transition.

Exercise 15.1

Derive an expression for dP/dT for a second-order transition by considering the variation

of S along the transition line.

Hint

A Maxwell relation can be used to transform the result into well-known parameters.

Solution

dS = (∂ S/∂ T )

dT + (∂ S/∂ P)

dP = (C

/T )dT − V αdP since (∂ S/∂ P)

−(∂V/∂ T )

On the transition line, where (dS) = 0, we get dP/dT = C

/VTα.

15.2 Order–disorder transitions

Let us consider an ordering phenomenon in a phase with a crystal symmetry such that the

properties can be expressed as even functions of the order parameter ξ .Asdemonstrated

326 Limit of stability and critical phenomena

(a) (b)

Figure 15.3 Molar Gibbs energy diagram illustrating the properties of a substance showing a

second-order transition. The dashed line in (b) represents unstable states, shown as points of

maximum in (a).

by Landau and Lifshitz [28] the simplest form of the Gibbs energy expansion in the

neighbourhood of the transition from disordered to ordered state would be

= g

ξξ

ξξξξ

, (15.3)

where g

ξξ

= ∂

/∂ξ

, etc., and g

, g

ξξ

and g

ξξξξ

may vary with temperature and

composition although variations in composition will not be considered yet. In order to

place the minimum of G

in the region close to ξ = 0, where the G

expression is

supposed to hold, it is necessary to make g

ξξξξ

> 0. In order to predict an ordered state

at low temperatures but not at high, it is necessary to assume that g

ξξ

is negative at low

temperatures and positive at high. The equilibrium value ξ

can be found from

/dξ = g

ξξ

ξ +

ξξξξ

= 0. (15.4)

The disordered, high-temperature state is described by ξ

= 0. At low temperature there

are two other solutions

=±(−6g

ξξ

ξξξξ

)

1/2

. (15.5)

By symmetry these two solutions are physically equivalent. They only exist as long

as g

ξξ

< 0 and they approach ξ

= 0asg

ξξ

approaches 0. The transition point would

thus be given by g

ξξ

= 0. Below the temperature where this occurs, the solution ξ

= 0,

representing a disordered state, would give a G

maximum and the disordered state

would thus be unstable here. Figure 15.3(a) demonstrates the shape of G

at temperatures

above and below the transition point, T

.Figure 15.3(b) shows how ξ

, obtained from

the minima, varies with temperature.

Let us now examine how we can calculate the limit of stability for the disordered state.

The condition would be simply



∂

∂ξ



T,P,comp.,N

= 0, (15.6)

since we have decided not to consider variations in composition yet. We get directly

ξξ

ξξξξ

= 0, (15.7)

15.2 Order–disorder transitions 327

but the stability condition can only be applied to states of equilibrium. Thus, we must

insert the equilibrium value, which is ξ

= 0 for the disordered state, yielding the limit of

stability at g

ξξ

= 0 for the disordered state when cooled from a high temperature. This

limit of stability thus falls on the transition point. When inserting the expression for ξ

in the ordered state we ﬁnd

ξξ

=−

ξξξξ

= 3g

ξξ

. Thus, g

ξξ

= 0. (15.8)

The limit of stability for the ordered state when heated from a low temperature also falls

on the transition point. That is typical of second-order transitions.

It is interesting to insert the equilibrium value ξ

in Eq. (15.3) for G

and thus to

obtain Gibbs energy expressions at equilibrium for ξ.

dis

= g

in disordered state (15.9)

ord

= g

−

ξξ

ξξξξξξ

in ordered state. (15.10)

At the transition point G

dis

= G

ord

and dG

dis

/dT = dG

ord

/dT because g

ξξ

= 0 there,

but the second-order derivatives are different, conﬁrming that this transition is of second-

order.

In order to model a ﬁrst-order transition one can either remove the symmetry by

introducing a ξ

term or one can keep the symmetry but introduce a ξ

term. With the

latter alternative we obtain

= g

ξξ

ξξξξ

720

ξξξξξξ

. (15.11)

In this case we must take g

ξξξξξξξ

> 0 and g

ξξξξ

< 0. Equilibrium requires that

/dξ = g

ξξ

ξ +

ξξξξ

120

ξξξξξξ

= 0. (15.12)

One solution is the disordered, high-temperature state, ξ

= 0, but one also ﬁnds low-

temperature states

=−10g

ξξξξ

ξξξξξξ

± [100(g

ξξξξ

ξξξξξξ

)

− 120g

ξξ

ξξξξξξ

]

1/2

. (15.13)

The ‘+’ sign gives a new minimum and the ‘–’ sign gives a maximum in between.

Figure 15.4 illustrates how G

varies with ξ above and below a temperature of equilib-

rium between the two states, the transition temperature, T

,where the minima fall on the

same level.

It is evident that the low-temperature minimum exists only as long as

100(g

ξξξξ

ξξξξξξ

)

− 120g

ξξ

ξξξξξξ

≥ 0 (15.14)

ξξ

≤ g

ξξξξ

/1.2g

ξξξξξξ

, (15.15)

and ξ

does not approach zero at any temperature. Wherever the transition occurs, it must

occur with a discontinuous jump in ξ and will thus be of ﬁrst order. The ordered state

can exist as a metastable state above the point of transition. The limit of stability for the

328 Limit of stability and critical phenomena

stability limits

(a)

(b)

Figure 15.4 Molar Gibbs energy diagram illustrating the properties of a substance showing a

ﬁrst-order transition. The black dots in (b) represent the two limits of stability. Metastable

states (exhibiting a minimum with a higher G

value than another minimum at the same

temperature) are represented by thin lines, and unstable states (shown as points of maximum) by

a dashed line.

ordered state is obtained from

/dξ

= g

ξξ

ξξξξ

ξξξξξξ

= 0. (15.16)

By inserting the equilibrium value ξ

for the ordered state from Eq. (15.5) and solving

for g

ξξ

we ﬁnd the limit of stability at the temperature where

ξξ

= g

ξξξξ

/1.2g

ξξξξξξ

. (15.17)

As expected, the limit of stability occurs when the low-temperature minimum disap-

pears by merging with the maximum and forming a point of inﬂexion.

By inserting the equilibrium value of ξ for the disordered state, ξ

= 0, we ﬁnd another

limit

/dξ

= g

ξξ

= 0. (15.18)

The disordered state thus becomes unstable at the point where g

ξξ

turns negative.

Between the two limits, g

ξξ

= 0 and g

ξξ

= g

ξξξξ

/1.2g

ξξξξξξ

, one of the states is stable

and the other is metastable. The ﬁrst-order transition between the states occurs where

they change roles. The exact position can be evaluated from the condition that G

has

the same value for the two states, somewhere between T

and T

in Fig. 15.4.Onthe

other hand, in a system showing a second-order transition, a state is never metastable on

the wrong side of the transition point because that is also the limit of stability and there

is only one such limit.

It is worth emphasizing that for a second-order transition Landau’s approach is not

a special model because it only applies at small ξ values and it says nothing about the

temperature dependencies of the coefﬁcients. Any analytical model can be represented

by aTaylor series expansion near the transition point and will thus predict the temperature

dependencies. If g

= g

ξξξ

= 0 and g

ξξξξ

> 0atallT, and if g

ξξ

goes through zero at

some value of T, then the model predicts a second-order transition and all the results for

transition obtained from Landau’s approach apply. On the other hand, if g

ξξξξ

< 0 then

15.2 Order–disorder transitions 329

the model does not predict a second-order transition but maybe a ﬁrst-order transition.

However, in that case the characteristics of the transition are not given completely by the

properties at low values of ξ .Inorder to examine an analytical model of this kind, it is not

enough to retain just one more term, ξ

,inthe series expansion and the result obtained

above does not apply in all its details. For a ﬁrst-order transition, Landau’s approach with

the choice of only three terms, ξ

, ξ

and ξ

, represents a special model and should be

regarded just as a means of demonstrating schematically the characteristics of such a

transition.

Exercise 15.2

Use the mathematical description of the ﬁrst-order transition and calculate exactly where

the transition point falls. Show that it falls between the two limits.

Hint

The two minima must have the same G

value at the transition.

Solution

Equations (15.11) and (15.12) yield g

= g

+ (1/2)g

ξξ

+ (1/24)g

ξξξξ

(1/720)g

ξξξξξξ

and g

ξξ

ξ + (1/6)g

ξξξξ

+ (1/120)g

ξξξξξ

= 0.

The most important variables are g

ξξ

,which may go through zero, and ξ.

Elimination of g

ξξ

between the two equations yields ξ

=−15g

ξξξξ

ξξξξξξ

Insertion of ξ

from Eq. (15.5) into Eq. (15.12) yields g

ξξ

= (1/6)g

ξξξξ

(−15g

ξξξξ

ξξξξξξ

) + (1/120)g

ξξξξξξ

· (−15g

ξξξξ

ξξξξξξ

)

= g

ξξξξ

/1.6g

ξξξξξξ

This occurs at a temperature between those for the two limits of stability according to

Eqs (15.17) and (15.18).

Exercise 15.3

Trytodescribe a second-order transition with the asymmetric expression G

= g

(1/2)g

ξξ

+ (1/6)g

ξξξ

+ (1/24)g

ξξξξ

Hint

Calculate the equilibrium value of ξ for the ordered state and examine if it can approach

zero gradually.

Solution

The equilibrium value is obtained from dG

/dξ = g

ξξ

ξ + (1/2)g

ξξξ

(1/6)g

ξξξξ

= 0.

For the ordered state we get ξ

=−(3/2)g

ξξξ

ξξξξ

± [(9/4)(g

ξξξ

ξξξξ

)

−

ξξ

ξξξξ

]

1/2

330 Limit of stability and critical phenomena

It is evident that ξ

cannot approach zero gradually unless g

ξξξ

= 0which would

make G

symmetric. The asymmetric G

expression can only describe a ﬁrst-order

transition.

We can conclude that to describe a second-order transition we need a symmetric G

function. On the other hand, a symmetric G

function can describe a second-order or a

ﬁrst-order transition, as demonstrated above.

15.3 Miscibility gaps

It sometimes happens that a two-phase coexistence line in the T, P phase diagram ends

at a critical point and this always happens for the liquid–vapour line. Above the crit-

ical point one can move continuously from a high density, characteristic of a liquid,

to a low density, characteristic of a vapour (see Fig. 15.5). A similar phenomenon can

occur in binary systems under constant pressure (see Fig. 15.6). Such phase ﬁelds are

often called miscibility gaps and the top, which is a critical point, is called consolute

point.

In the binary case the condition for the stability limit would be (∂

/∂x

)

T,P

≡

= 0. However, for most compositions this would give a point falling inside the mis-

cibility gap where the homogeneous state is not the most stable one. As explained

in Section 7.2, the stability condition here deﬁnes inﬂexion points and Fig. 15.7

gives G

curves for a series of temperatures demonstrating that the two inﬂexion

points move together to a point at the top of the miscibility gap. The consolute point

can thus be found by combining the stability condition already given with a new

condition,



∂

∂x



T,P

= 0. (15.19)

We thus have two equations and can evaluate two unknowns, the temperature and

the composition of the consolute point. For the miscibility gap in a unary system the

top can be found in two ways because the limit of stability can be expressed in two

ways,

=−



∂ P

∂V



V κ

= 0 and F

VVV

= 0 (15.20)

=−



∂T

∂ S



= 0 and H

SSS

= 0. (15.21)

The thin line in Fig. 15.6(b) is the locus of points representing the stability limit

and the diagram conﬁrms that it touches the top of the miscibility gap. The consolute

point is thus the only point where the stability limit can be reached by a stable system.

It is regarded as a critical point because two coexisting states become identical there.

For all other compositions the homogeneous system turns metastable on cooling before

reaching the stability limit. It should be noted that the transition point for a second-order

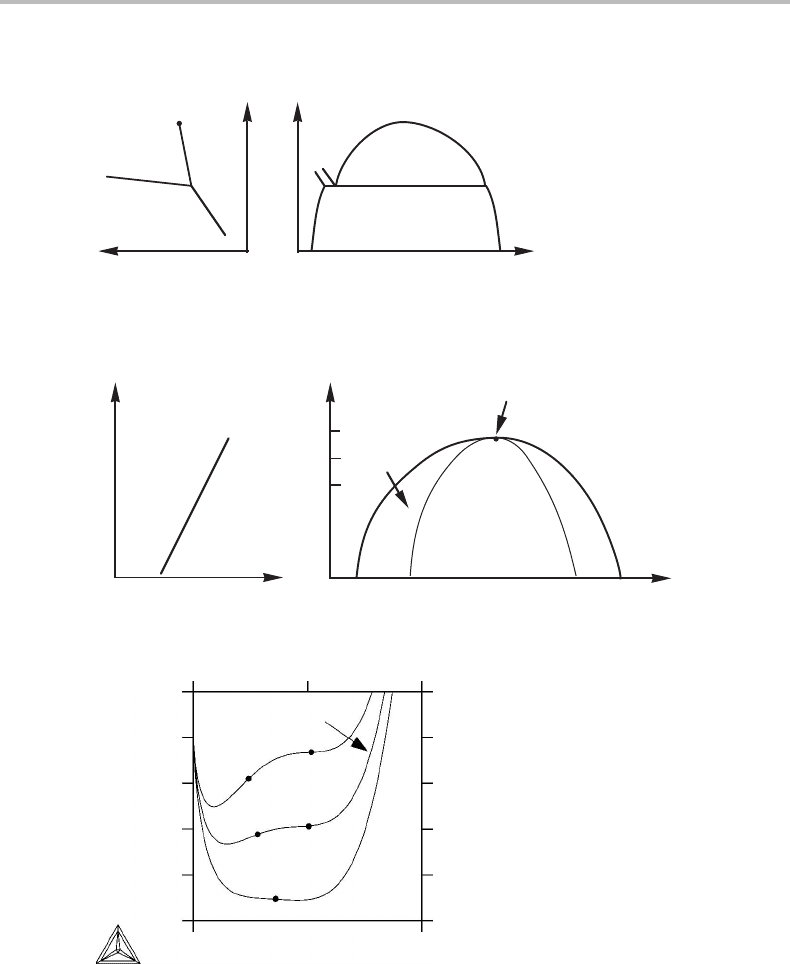
15.3 Miscibility gaps 331

(a) (b)

Figure 15.5 Phase diagram for a unary system showing the liquid + vapour miscibility gap.

unstable

region

metastable

region

consolute point

(critical point)

(a) (b)

Figure 15.6 Phase diagram for a binary system at constant P, showing a solid miscibility gap.

200

575 K

525 K

625 K

−200

−400

−600

−800

1.0

Figure 15.7 Gibbs energy curves at a series of temperatures through the fcc miscibility gap in the

Al–Zn system at constant P. The inﬂexion points are marked with black dots. They represent the

spinodal. Just below 625 K they coincide and form a critical point.

transition is not a critical point in this sense because the ordered and the disordered states

never coexist as two different phases if the transition is second-order.

The line representing the stability limit in a miscibility gap is called a spinodal curve

or simply a spinodal or a spinode because it falls on a sharp point (spine meaning

thorn)inproperty diagrams with potential axes. An example is shown in Fig. 15.8.

332 Limit of stability and critical phenomena

−16.4

−16.6

−16.8

−17.0

−17.2

−17.4

−17.6

−24.0 −23.0

(kJ/mol)

Figure 15.8 Property diagram at constant T and P for a binary system with a miscibility gap, the

fcc phase in Al–Zn at 525 K.

In this connection it is common to call the phase boundary of the miscibility gap a

binodal.

The critical point on a miscibility gap extends into a line when a third compo-

nent is added, into a surface when a fourth component is added, etc. According to

Section 6.6 the limit of stability of a multicomponent system, i.e. the spinodal, is deﬁned



∂g

∂x



T,P,g

,...g

c−1

= 0. (15.22)

The critical point is found by also applying the condition



∂

∂x



T,P,g

,...,g

c−1

= 0. (15.23)

It should be remembered that g

is the notation for (∂G

/∂x

)

...x

c−1

.InSection 6.6

it was shown that the stability condition can be transformed into such quantities, using

the Jacobian method. For a ternary system the result can be written as





= g

− (g

)

= 0. (15.24)

Using the same technique the condition for a critical point can be transformed, but the

result will be more complicated (see, for instance, [29]). In the ternary case it can be

written as

− 3g

233

) + 3g

223

)

− g

222

)

= 0. (15.25)

Equation (15.25) can be modiﬁed in several ways using g

= g

which holds

on the spinodal. For the binary case the result is simply g

222

= 0, which is just a nota-

tion for ∂

/∂x

= 0when x

is treated as the independent variable that is kept

constant.

15.3 Miscibility gaps 333

(a) (b)

Figure 15.9 Progress of reaction in a miscibility gap for a series of compositions, demonstrating

that this is a gradual transformation for all compositions, but it is not a second-order transition.

The reason why one cannot ﬁnd the critical point in a ternary case by applying g

222

= 0

and g

333

= 0isthat the most dangerous ﬂuctuation may not be parallel to any of the

two composition axes. It should be noted that this is the reason why the condition for

the stability limit is primarily given under constant potentials, not extensive or molar

quantities.

For the binary miscibility gap it may be instructive to introduce an internal variable in

order to describe the progress of the reaction as a function of temperature in a system with

ﬁxed composition. We can deﬁne an internal variable having the following equilibrium

value

(T ) = [x

(T ) − x

][x

− x

(T )], (15.26)

where x

(T ) and x

(T ) are the equilibrium compositions on the two sides of the misci-

bility gap and x

is the average composition. In Fig. 15.9 this variable is plotted against

temperature for three values of the average composition, x

, equal to x

, x

and x

respectively. Figure 15.9(b) can be compared with Figs 15.2(c) and 15.2(d).Itisevident

that this will be a gradual transformation for all compositions.

Exercise 15.4

Consider a unary system with a liquid(l) + vapour(v) miscibility gap in the T, V

phase

diagram. Within the gap there is a spinodal curve, representing the limit of stability.

Examine what happens to the spinodal in the diagram if P is introduced instead of V

Furthermore, sketch a µ

, P property diagram at constant T.

Hint

The spinodal, has two branches. Denote the stability limit of liquid by S

and of vapour

. Each one represents the end of a metastable range and should thus be situated on the

‘wrong’ side of the line of coexistence in the P, T diagram.

In the property diagram each phase is represented by a line and they intersect in such

away that the stable phase always has the lowest µ

value. They only extend to their

limits of stability.

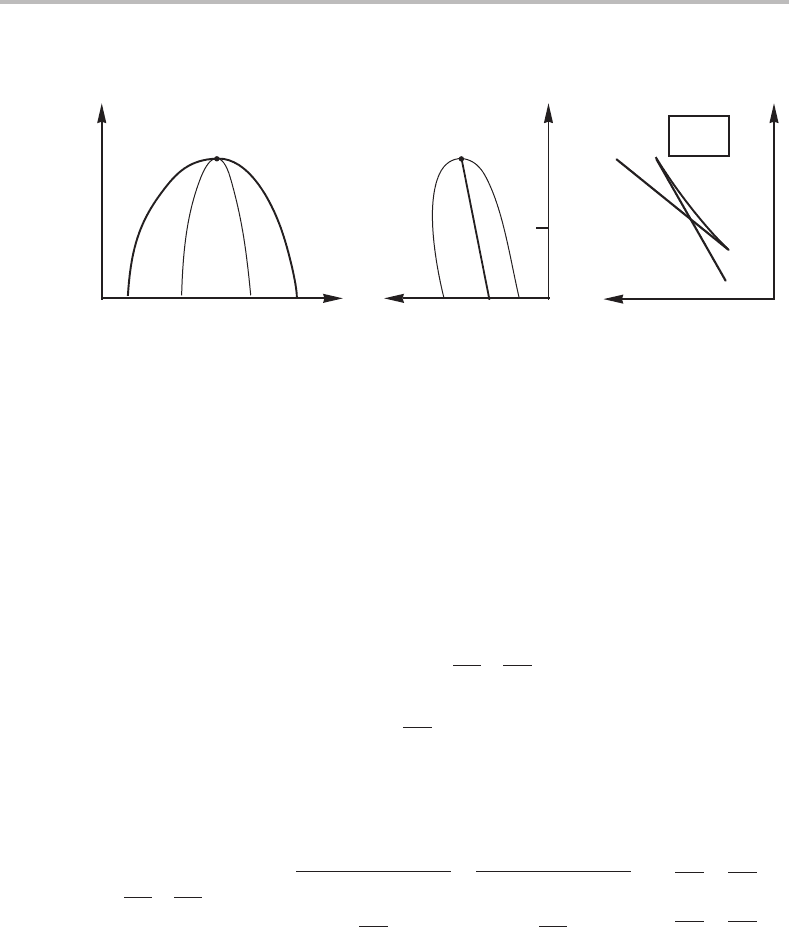
334 Limit of stability and critical phenomena

T = T

(a) (b) (c)

Figure 15.10 Solution to Exercise 15.4.

Solution

The solution is presented in Fig. 15.10.

Exercise 15.5

Transform the condition for a critical point in a ternary system, (∂

/∂x

)

= 0, to the

variables x

and x

using Jacobians and conﬁrm Eq. (15.25).

Hint

The derivative should ﬁrst be expressed as



∂

∂x



∂g

∂x





. Use a method similar to

the one applied when showing that



∂g

∂x





= g

− (g

)

Exercise 6.6.

Solution



∂

∂x



∂g

∂x







∂(g

− (g

)

∂x

∂(g

− (g

)

∂x

∂g

∂x

∂g

∂x



∂x

∂g

∂x

∂g

∂x



= [g

333

− g

· 2g

233

+ g

· (g

)

223

/(g

)

− g

233

+ g

· 2g

223

− g

· (g

)

222

/ (g

)

] / g

= g

333

− 3g

233

) + 3g

223

/ g

)

−

222

)

= 0.

15.4 Spinodal decomposition

Thermodynamically, a system inside the spinodal is unstable with respect to compo-

sitional ﬂuctuations and one could expect the system to decompose to a mixture of