Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis

Подождите немного. Документ загружается.

14.3 Quasi-adiabatic phase transformation 305

(α+β)

(α/β)

(β/α)

∆H

(a) (b)

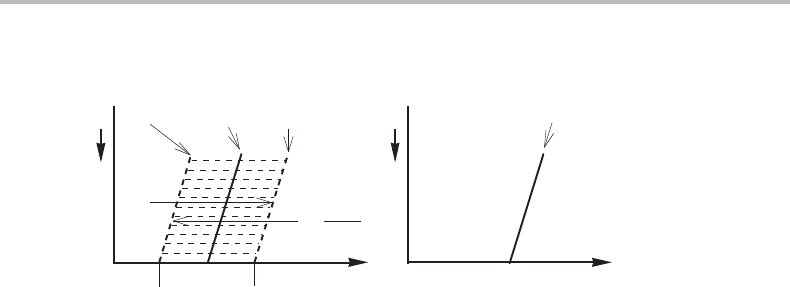
Figure 14.2 Phase diagram for isobaric and adiabatic conditions in a unary system. Notice that

the α and β one-phase ﬁelds in the P, T diagram overlap in a region around the equilibrium

temperature.

could form, it would not be stable because it is inside the stable one-phase ﬁeld for β

according to the T, P diagram in Fig. 14.1.Partofα could thus transform back to β.In

the next section we shall examine a more realistic model.

Exercise 14.1

Estimate the internal entropy production when 1 mole of a pure substance transforms

adiabatically from α to β when the temperature of α is T above the value where there

is no entropy production.

Hint

Of the two conditions used in the text, only one holds here, H = 0, but 

S is still

equal to S and can be calculated from S

+ C

ln(T

), if C

is constant and

equal in the two phases.

Solution

= T

+ H

/2C

+ T = T

+ T

S

/2C

+ T .

From 0 = H = H

+ C

− T

) = T

S

+ C

− T

)weget T

− T

S

= T

− T

S

/2C

+ T ; 

S = S

− C

ln(T

) =

S

− C

ln{[1 − T

(S

/2C

)/(T

+ T )]/[1 − T

(S

/2C

)/(T

+ T )]}

∼

S

− C

(S

)(T

+ T )

∼

S

T /T

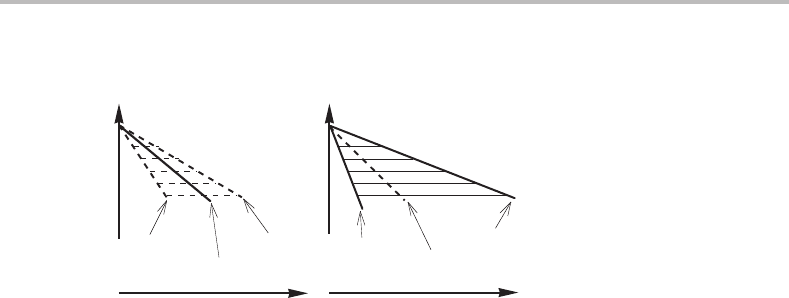
14.3 Quasi-adiabatic phase transformation

Let us now examine if there are conditions under which the transformation can occur by

a steady-state process, i.e. without a gradual change of the conditions at the migrating

306 Partitionless transformations

= T

∆H

(a) (b)

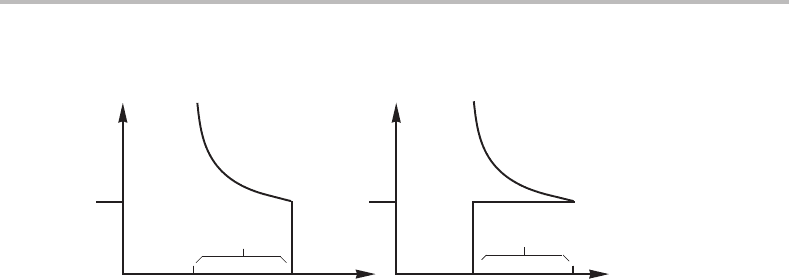
Figure 14.3 Steady-state conditions for a quasi-adiabatic β → α transformation under constant

P. The growing α has the same enthalpy as the initial β.

interface. The growing α should then have a uniform temperature, T

,but the tem-

perature may vary inside the parent β. The temperature proﬁle can be illustrated by

Fig. 14.3(a) which has been drawn under the assumption of local equilibrium at the

interface. All of the α phase must be at the equilibrium temperature, T

.Inorder for this

to be a steady-state process it is necessary that α has the same enthalpy as the bulk of

the β phase. This is illustrated in Fig. 14.3(b) and the following equations are obtained

if the heat capacity can be approximated as constant and the same in both phases.

H = H

+ C

− T

) = 0 (14.7)

= T

− H

= T

− H

. (14.8)

The reaction can thus be essentially adiabatic if it is possible to change the temperature

of the whole β system to T

− H

before the nucleation of α occurs. This model

thus requires twice as large a T as the truly adiabatic model. This is a demonstration

of the fact that a deviation from local equilibrium results in less need of driving force.

After a transient period, during which an enthalpy spike of height H

will develop in

the β phase at the migrating interface, steady-state conditions will be established and

then maintained towards the end of the reaction. The duration of the transient period

and the width of the temperature spike in the parent phase will depend upon the rate of

transformation and the rate of heat ﬂow. We can use the phase diagrams, given below,

for a summary of our conclusions (see Fig. 14.4).

Point 1 in Fig. 14.4 is the isothermal transformation temperature for β.Aβ phase

cooled just below that point could start to transform to α but the progress of the trans-

formation would be directly controlled by the further extraction of heat from the system.

The growing α phase will be at point 2. If a β phase could be cooled to point 3 before

the transformation starts, then the transformation could, in principle, occur very quickly

and adiabatically and the α phase would be at point 4. However, if the phase interface

does not move with an extremely high velocity, there will be heat conduction into the

remaining β phase and it will no longer be able to transform adiabatically but would

depend upon further heat extraction. Finally, if a β phase could be cooled to point 5

before the transformation starts, then the transformation could occur without any further

heat extraction even if there is time for heat conduction. All of the α formed would be

14.3 Quasi-adiabatic phase transformation 307

(α/β)

(β/α)

(α+β)

(α/β)

(β/α)

(α+β)

(a) (b)

Figure 14.4 Phase diagram illustrating the conditions for a quasi-adiabatic transformation in a

unary system. Subscript T indicates isothermal conditions. Subscript H indicates adiabatic

conditions because P is kept constant.

at point 2 and β at the interface would be at point 1. The transformation could occur

in a steady-state fashion where the growing α phase forms at T

. The initial β is at a

lower temperature (compare point 2 in the P, T phase diagram with point 5) but has the

same enthalpy (compare point 2 in the P, H

phase diagram with point 5). This type of

reaction could be called a quasi-adiabatic transformation. It is interesting to note that it

occurs when the parent phase, by cooling, is entering into the ﬁeld for the new phase in

the P, H

diagram.

It is usually assumed that a transformation starts from a stationary nucleus and picks

up speed during an initial transient period. It would then be natural to expect a situation

somewhat similar to Fig. 14.3 to be established after some short time. It is an interesting

question whetherit could later develop into a trulyadiabatic mechanism. The requirement

would be that the speed becomes so fast that the temperature spike in the parent phase

becomes so thin that it disappears between the atoms. A simple calculation would show

that the thickness should be less than about D/υ,where D is the diffusion coefﬁcient of

heat and υ is the growth rate. This transition turns out to be very unlikely.

Exercise 14.2

Figure 14.5 gives the relations between S

and H

for bcc and liquid W. The melting

point is marked with an asterisk for each phase. Evaluate the change of entropy during

quasi-adiabatic melting and solidiﬁcation.

Hint

The growing phase must be stable in contact with the parent phase at the interface, i.e., it

must grow at the melting temperature. The bulk of the parent phase must be at a different

temperature in order to have the same enthalpy as the growing phase.

Solution

The melting point on the liquid curve (the asterisk) represents the growing liquid and

the bulk of the parent bcc is situated exactly below it. The change of entropy can be read

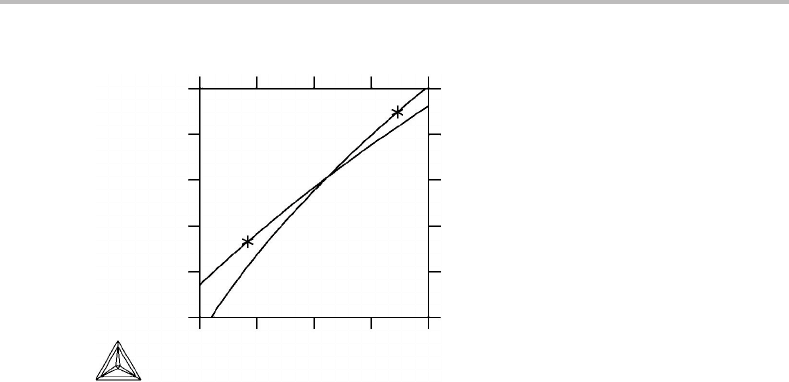
308 Partitionless transformations

125

120

120 140 160 180

115

110

105

100

Enthalpy, H-H

SER

(kJ/mol)

Entropy, S (J/molK)

bcc

Liquid

Figure 14.5 See Exercise 14.2.

as +1.5J/mol, K and for solidiﬁcation as +2.8J/mol, K. In both cases the entropy is

produced in the thermal spike in front of the interface.

Exercise 14.3

Estimate how fast a transformation should be in order to reach truly adiabatic conditions.

Hint

The diffusion coefﬁcient D for heat conduction is about 10

−5

/s. The atomic distances

are about 10

−10

Solution

D/υ < 10

−8

yields ν>10

−5

/10

−10

= 10

m/s. This is higher than the speed of sound.

14.4 Partitionless transformations in binary system

We shall now examine a partitionless transformation, i.e., a transformation where the

components do not partition between the parent phase and the product, and we shall

ﬁnd striking similarities with the adiabatic case. We shall use the combined law from

Eq. (3.27) because temperature and pressure will be kept constant in addition to

composition.

Ddξ =−SdT + V dP + µ

− dG =−dG. (14.9)

In this case G plays the same role as S from Eq. (14.2) under adiabatic conditions. The

driving force for the reaction is D =−dG/dξ and for D = 0wewould have a reversible

reaction which would occur without a change of the Gibbs energy but inﬁnitely slowly.

The reaction could proceed with a measurable rate if D > 0, i.e. dG < 0. Partitionless

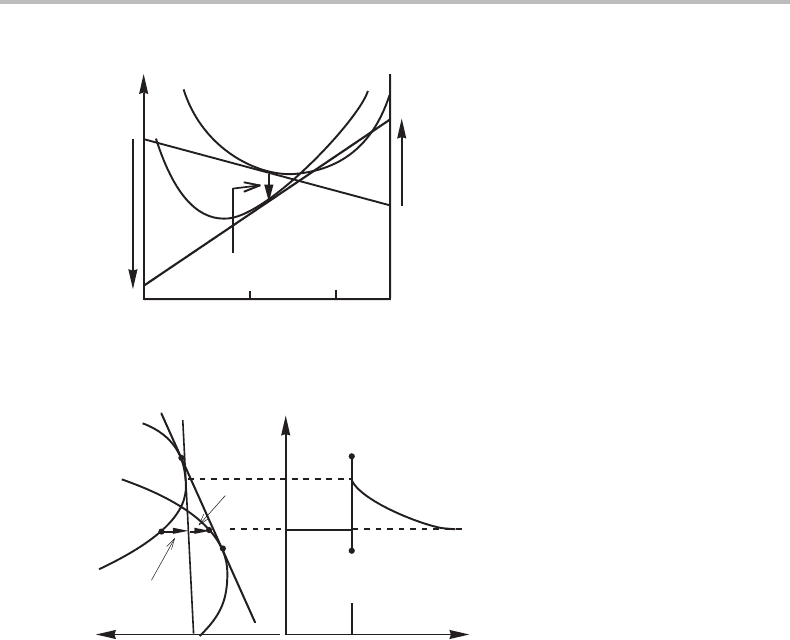
14.4 Partitionless transformations in binary system 309

∆ µ

∆µ

α/β

β/α

−∆G

= G

− G

Figure 14.6 Conditions for a true diffusionless transformation.

int

diff

Figure 14.7 Crude model for deviation from local equilibrium under a quasi-diffusionless

transformation.

transformations were discussed in Section 7.8.Weshall now examine such a reaction in

more detail and discuss two limiting cases depending on whether any diffusion is

involved. In principle, it could be completely diffusionless,acase that is illustrated

in Fig. 14.6.However, there could also be some diffusion, e.g. in a thin pile-up of a

component which is pushed forward in front of the advancing interface. It is illustrated

in Fig. 14.7 and resembles the quasi-adiabatic case in Fig. 14.3 and may be regarded

as quasi-diffusionless. Both cases are illustrated in Fig. 14.8 which can be compared

with Fig. 14.4 for the adiabatic cases. The dashed line in the T, x

diagram, denoted

by T

, corresponds to the dashed line in the P, H

diagram, which showed where α

and β have equal values of H

.Onthe T

line, α and β have equal values of x

and

equal values of G

, i.e., a true diffusionless transformation. The other limiting case is

found when there is full local equilibrium at the migrating interface, according to the full

lines in Fig. 14.8(b), similar to the quasi-adiabatic case in Fig. 14.4(b).Itisthe limiting

case of a quasi-diffusionless transformation and could be called local-equilibrium parti-

tionless transformation or simply LE-partitionless transformation. It was discussed in

Section 7.8 and illustrated in Fig. 7.21.

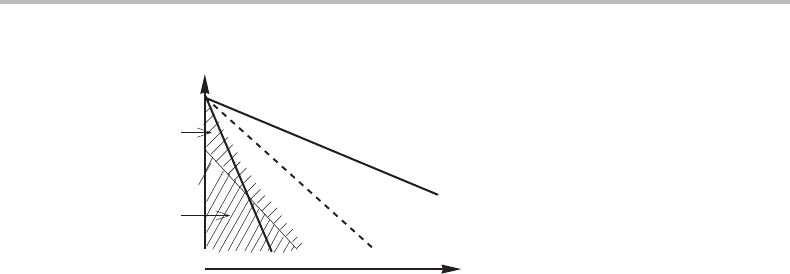
The true diffusionless transformation is easy to understand. If a β alloy is cooled below

the T

line, where α of the same composition has the same G

value, then G

may

310 Partitionless transformations

(β/α)

(α/β)

(α+β)

(β/α)

(α/β)

(a) (b)

Figure 14.8 Phase diagram for a binary system illustrating the conditions for diffusionless and

LE-partitionless transformations. The full lines show the phase boundaries under equilibrium

(constant T, P and µ

). The dashed lines hold if there is no diffusion.

decrease by the β → α transformation even without any change of the composition.

The molar Gibbs energy diagram in Fig. 14.6 demonstrates that µ

will increase by

that transformation, which corresponds to the increase of T during the true adiabatic

transformation.

In practice, it is seldom possible to avoid diffusion completely. It would be necessary

that the mathematical width of the pile-up in Fig. 14.7 is below atomic dimensions. The

growth rate should be of the order of D/d or higher. D is the diffusion coefﬁcient and d is

about 10

−10

m. Otherwise, the transformation could not be regarded as diffusionless. On

the other hand, at diffusion-controlled transformations the growth rate may often be low

enough to make the LE-partitionless transformation a reasonably good approximation.

Figure 14.7 demonstrates a more general case where there is some deviation from local

equilibrium at the interface and the compositions at the interface do not fall on the points

of tangency for the common tangent.

In metallic materials there are two well-known partitionless transformations called

‘martensitic’ and ‘massive’. The martensitic transformation is usually very rapid and

comes close to the true diffusionless case but its interface migrates with an atomic

mechanism that creates strong stresses which require a high driving force. This type

of transformation can very well occur far inside the α + β two-phase ﬁeld but only

at a considerable distance below the T

line due to the necessity of a driving force.

The massive transformation is rapid but not extremely rapid. There may be time for

individual atoms to diffuse across the interface and maybe even for a pile-up to form.

This transformation may thus fall well between the two limiting cases.

An interesting problem may be mentioned in this connection. Figure 14.6 demonstrates

that the chemical potential of B increases as it crosses the interface and moves from β

to α. One should ask what forces the B atoms to move against their driving force. In

the LE-partitionless transformation the problem is solved by the presence of the pile-up.

As it moves in front of the migrating interface, it gradually lifts the B atoms to higher

potential as illustrated in Fig. 14.7.For the martensitic transformation the explanation

must be that all atoms cross the interface with some kind of a cooperative mechanism.

Forarapid massive transformation there may not be a sufﬁciently well developed pile-up

14.5 Partial chemical equilibrium 311

massive

martensite

Figure 14.9 Solution to Exercise 14.4.

and the mechanism of transfer of atoms across the interface must be partly cooperative.

This will be further discussed in Chapters 16 and 17.

Exercise 14.4

Given the phase diagram in Fig. 14.6, mark the regions where one could expect the

massive or the martensitic transformations β → α. Suppose that the martensitic trans-

formation requires an undercooling below T

which is independent of the composition

and that the massive transformation occurs with some small deviation from equilibrium.

Hint

Martensite will normally grow much faster because it requires no diffusion. Martensite

would thus predominate in a region where both types of transformation could occur, in

principle.

Solution

The solution is given in Fig. 14.9.

14.5 Partial chemical equilibrium

In a ternary alloy it could very well happen that one of the elements diffuses very much

faster than the other two, for example if it is an interstitial solute. It is then possible that a

new phase forms with a different content of the mobile element but without a change of

the relative contents of the other two. Such a transformation would be partly partitionless.

Hultgren [26] proposed that it could even occur without any diffusion of the latter two

elements and used the term paraequilibrium to describe the local equilibrium at the

phase interface under such a transformation. We shall now examine that kind of local

equilibrium. Hultgren studied systems with Fe, C and a metallic solute which we shall

denote by M. We shall keep those symbols but Fe could represent any element, C any

mobile element and M any element as sluggish as Fe.

312 Partitionless transformations

Under full local equilibrium at a phase interface, there is no driving force on the

interface as shown by the following form of the combined law Eq. (3.33),

Ddξ =−SdT + V dP −  N

dµ

= 0, (14.10)

because T, P and all µ

have the same values on both sides of the interface. When

a transformation occurs under paraequilibrium, µ

has the same value on both sides

because C is very mobile, but µ

and µ

have different values. Instead, u

and u

have the same values if u

is deﬁned as N

/(N

+ N

). It is thus useful to consider the

combined law in a new form which can be derived as follows,

Ddξ =−SdT + V dP −  N

dµ

(14.11)

Ddξ/(N

+ N

) =−S

m12

dT + V

m12

dP − u

dµ

± (µ

+ µ

)

=−S

m12

dT + V

m12

dP − u

dµ

+ µ

− d(u

+ u

(14.12)

The subscript ‘m12’ is explained in Section 4.3. Under paraequilibrium dT = dP =

dµ

= du

= 0 and we ﬁnd

Ddξ/(N

+ N

) =−d(u

+ u

) = 0. (14.13)

The driving force has here been put to zero for a transformation occurring under parae-

quilibrium conditions because, ideally, paraequilibrium is supposed to be a kind of local

equilibrium. It is thus necessary that u

+ u

has the same value on both sides

of the interface. Of course, T, P and µ

must also have the same values on both sides.

The new quantity that must have the same value in both phases is simply an average

value for Fe and M, as if they together have formed a new element. The quantity can be

written in various ways because G

m12

= u

+ u

= G

m12

− u

− x

1 − x

. (14.14)

Suppose the three elements can form a compound θ of the formula (Fe, M)

with

a + c = 1. For paraequilibrium between θ and a solution phase, γ,weﬁnd



− cµ





− x

1 − x



. (14.15)

It should be noted that u

+ u

is a characteristic state function. It was actually

derived in Section 13.6 in a slightly different way and written as G − N

In a molar Gibbs energy diagram the tie-line between the two phases in paraequilibrium

is directed towards the C corner. It falls on a common tangent line to the two Gibbs

energy surfaces but not on the common tangent plane. Figure 14.10 demonstrates that

the common tangent line for paraequilibrium, which must go through the C axis, is

situated above the common tangent plane that holds for full equilibrium. The chemical

potential of C will thus be slightly different.

Figure 14.11(a)–(d) gives various versions of the phase diagram showing the equilib-

rium between two solution phases, α and γ,atsome convenient T and P values. Instead

of using the chemical potentials, µ

and µ

,asaxes the chemical activities, a

and

,have been used in order to make the diagram show low contents of C and M where

the chemical potentials would approach negative inﬁnity. It is interesting to note that

14.5 Partial chemical equilibrium 313

Figure 14.10 Molar Gibbs energy diagram for a ternary system illustrating the paraequilibrium

conditions. The common tangent line from the C axis is situated above the common

tangent plane.

(α/γ)

(α+γ)

(α/γ)

(γ/α)

(α/γ)

(a) (b)

(d)(c)

Figure 14.11 The phase diagram for a ternary system at constant T and P, drawn with different

sets of axes in order to illustrate the paraequilibrium conditions (dashed lines), assuming that C

is the only mobile component.

Figs 14.11(a) and (b) are very similar to Fig. 14.6 but T has been replaced by a

.Infact,

the two reactions are very similar because the additional component in the present case

is compensated by the temperature being kept constant.

The point of equal Gibbs energy of α and γ on the binary Fe–M side has been marked

as T

in Fig. 14.11(d) because it belongs to the T

line in the binary T, x

diagram. It

is important to note that the two paraequilibrium phase boundaries fall inside the full

equilibrium two-phase ﬁeld. This is a general rule.

314 Partitionless transformations

(γ/α)

quasi-para

(γ/α)

quasi-para

(γ/α)

quasi-para

(a) (b)

(d)(c)

Figure 14.12 Dashed lines show the conditions for quasi-paratransformation γ → α in a ternary

system with a very mobile component C.

As in the binary case, discussed in the preceding section, we should also examine

the possibility of obtaining a partitionless (here of Fe and M) transformation under full

local equilibrium. That should be possible if there is a composition spike in front of the

migrating interface. The critical limit for a γ → α transformation to take place under

such quasi-paraequilibrium conditions is that the initial γ phase falls on the α phase

boundary in the a

phase diagram (see Fig. 14.12(b)). Again the conclusions are

very similar to the previous case. However, in the present case it is more common to use

an x

phase diagram (see Fig. 14.12(d)). It should be noticed that the critical limit

for a quasi-paratransformation will not fall on the α phase boundary in such a diagram

because γ and α must have the same µ

(i.e. a

) and that requires different x

Finally, we may compare the critical limit for the two partitionless kinds of growth

by means of Fig. 14.13.Itisinteresting to note that paraequilibrium with its devi-

ation from full local equilibrium requires less supersaturation of the parent γ. This

is in agreement with a more general principle mentioned in Section 14.1.Inprac-

tice, one should expect something between quasi-paraequilibrium and paraequilib-

rium depending on the mobilities of Fe and M, especially inside the interface, rela-

tive to the rate of migration of the interface. In the next section we shall give a more

detailed account of some phase transformations assuming that they take place under

quasi-paraequilibrium.

Exercise 14.5

In Fig. 14.11 there are two diagrams with dashed tie-lines. They hold for paraequilibrium.

In the other two diagrams the corresponding tie-lines have not been drawn. Indicate where

they should fall.